Handedness helps homing in swimming and flying animals

Abstract

Swimming and flying animals rely on their ability to home on mobile targets. In some fish, physiological handedness and homing correlate and dolphins exhibit handedness in their listening response. Here, we explore theoretically whether the actuators, sensors and controllers in these animals follow similar laws of self-regulation and how handedness affects homing. We find that the acoustic sensor (combined hydrophone-accelerometer) response maps are similar to fin force maps—modeled by Stuart-Landau oscillators—allowing localization by transitional vortex-propelled animals. The planar trajectories of bats in a room filled with obstacles are approximately reproduced by the states of a pair of strong and weak olivo-cerebellar oscillators. The stereoscopy of handedness reduces ambiguity near a mobile target, resulting in accelerated homing compared to even-handedness. Our results demonstrate how vortex-propelled animals may be localizing each other and circumventing obstacles in changing environments. Handedness could be useful in time-critical robot-assisted rescues in hazardous environments.

Introduction

Handedness, called dissymétrique by Louis Pasteur, is widely present in the universe, being found in all matter from atoms to human beings¹. The predominant right-handedness in man seen today is evidenced in the use of uni-manual tools or weapons in 5000 years of art, irrespective of geography². While a weak force acting on elementary particles causes handedness in atoms and molecules, it is not known how this conveys to the macroscopic scale and what the manifestations are. In man, left-handedness correlates with lower longevity³. In another example, right-handed scale-eating cichlid fish of Lake Tanganyika approach prey from the rear and snatch scales from their left flank and left-handed fish do likewise from the right flank⁴. Dolphins also exhibit handedness in their listening response^5,6. Despite widespread evidence of handedness, theoretical understanding is relatively lacking.

Here, we consider theoretically whether the propulsion aspects of swimming and flying animals—namely, the force production, sensing and control—are related dynamically and whether they exhibit handedness and if they do, does that produce any advantage in the goal of homing on a target. We take an approach where subjective social or environmental factors are absent.

Consider the preferential property of force fields and acoustic response in swimming animals. Fig. 1 shows the instantaneous vectors of the oscillatory force fields due to a pair of 10 cm span pectoral fins^7,8 and handedness in the acoustic response of a dolphin to 120 kHz transmitted beam patterns^5,6. The fins are rigid and have penguin-like planform, section and low aspect ratio. The force data is for a large range of fin kinematic parameters (roll and pitch amplitudes and pitch bias angle) and perhaps represents all possible ranges in typical penguins. At any instant of time, the net fin force acts at a distance of R_avg (defined later in eqn. 2) from the roll axis at the fin hinge location which is c/3 from the fin leading edge, where c is fin chord⁷. The force and sensor maps have directional preference and are not spherical. The global distribution of instantaneous force vectors in the laterally placed pair of flapping fins is disk-like, as is also the acoustic response (see Figs. S1c and S1d in Part A of the Supplementary Information (SI)). The behavioral measurements on captive dolphins show several differences in the receiving beam patterns between the lateral and dorsoventral planes and between the left and right sides in the lateral plane^5,6. For example, at 120 kHz, in the polar map, the receiving sensitivity extends to ±30° in the dorsoventral plane, but it extends to more than ±40° in the lateral plane. In the lateral plane of a dolphin, the receiving response is clearly asymmetric between the left and right sides. For example, between the 0 dB and −10 dB circular arcs, the receiving response is weaker on the left azimuthal side and stronger on the right azimuthal side, while between the −10 dB and −20 dB arcs, the sensitivity is reversed. In the present work, the consequence of similar more detailed handedness in the force field is examined.

Figure 1

Preferential distributions of actuator force field and acoustic response in the lateral and dorsoventral planes in swimming animals.

(a) Instantaneous force vectors due to a pair of pectoral fins based on biorobotic penguin fin model measurements⁷. (b) Dolphin beam pattern response in the lateral (solid red line) and dorsoventral (solid blue line) planes due to transmitted (chained red and blue lines, respectively) beam forms; adapted from Au^5,6. The dolphin origin in the lateral plane measurements is not shown but is similar to that shown for the dorsoventral measurements.

To understand optimal organization, consider the systemic properties of self-regulation. The propulsion of swimming and flying animals is an organized process because it involves the flapping of fins in a narrow range of Strouhal (St) numbers^9,10, St being defined non-dimensionally as fA/U, where f is the flapping frequency, A is the stroke (arc) length and U is the forward speed. The animals' propulsion is a self-regulating process that is tuned for maximizing efficiency^11,12, which can be modeled by van der Pol-like oscillators⁸. The parameters of the oscillator (the bifurcation properties) vary with the physical mechanism—such as vortex-based propulsion, vector sensing, or ion flow in the inferior-olive neurons of motion control (see Fig. 2a).

Figure 2

Schematic of the hypothesis of how vortex-propelled animals remain in persistent synchrony with their surroundings.

The controller, actuator and the sensors follow similar nonlinear oscillator dynamics. (a) Shows the dependence of fin force maps on Reynolds number Re_c in a low-aspect ratio hinged-fin, optimally twisting at constant optimal Strouhal number of 0.30⁸. (b) The unsteady force fields of the fins (actuators) radiate acoustic maps characteristic of their fin Reynolds number and Strouhal number. The sensors detect these acoustic maps. The vector match of one's own sensor (subscript p) to the other's actuator is shown by the Coptic letters shei () and sampi (). The brain provides olivo-cerebellar dynamic motion control.

To understand self-regulation, consider a linear system such as , where x is the state variable, dots represent time derivatives, is a damping parameter and is the frequency of oscillation of the system. The solution converges when ; the solution diverges when ; and the solution oscillates when . All of the behavior is scaled proportionate to the initial conditions; that is, a perturbation in the initial conditions is transmitted directly to the amplitude of the resulting dynamics. In contrast, consider a nonlinear system such as , where the nonlinear function , such that the constants and . For small values of x, f approximates the negative constant; for large x, nonlinearity dominates. If x starts small and increases, the solutions increase; but as x becomes large, the solutions decrease. The result is a sustained periodic set of oscillations that is a nonlinear process where all solutions, in the limit, converge to the periodic cycle (a so-called limit cycle). Irrespective of the value of x, ω remains in a narrow band. When the system is disturbed, it automatically introduces corrective actions by way of its nonlinear components causing it to maintain the oscillations, exhibiting auto-catalytic properties. This is called self-regulation. (An experimental demonstration of the disturbance rejection behavior of the single flapping fin is given in Bandyopadhyay et al¹³. (see Animations 1a and 1b in the SI).

If we assume that it is advantageous for swimming and flying animals to remain in persistent synchrony with the environment then the question is, how do they do that? We hypothesize that vortex-propelled swimmers, for example, are in persistent synchrony with their surroundings in the manner depicted in Fig. 2b where the elements (namely, the actuators, sensors and controllers) are each self-regulating. Consider a large and a small animal. Their optimally operating unsteady force actuators produce force fluctuation (F_x′) maps (():, , respectively)) appropriate to their fin chord (c) Reynolds number Re_c ( = Uc/υ, where U is the forward speed and υ is the kinematic viscosity of the medium) (see force field in Fig. 1a)⁸. Fig. 2a shows how the wake vortex dynamics changes with Re_c. The unsteady propulsive surfaces and their wake vortices remain coupled, having reciprocal exchanges of energy that maximize efficiency. The wake vortex train can be represented by a nonlinear oscillator whose bifurcation properties depend on St and Re_c. The force maps produce similar pressure fluctuation maps , , respectively. The lateral line sensors are assumed to measure pressure and tri-axial acceleration (or equivalent vectors in the case of Lorenzian sensors), which allows them to read these pressure maps. Behavioral experiments show that in fish schooling, lateral lines—not vision—are more important for determining neighbor's speed and direction¹⁴. The large animal reads the map of its target, and similarly, the small animal reads . In this manner the animals locate the noise source and the Re_c of the source. The motion control neurons have similar dynamical properties. In other words, the same types of nonlinear equations apply to the actuators, the sensors and the controllers. Handedness is defined as small differences in amplitude and sensitivity between the port and starboard directions. We examine the elements of this hypothesis theoretically and investigate how handedness affects homing. In the ensuing sections, the oscillators of the force actuator are modeled, the sensor response is given, the animal motion path is modeled and the effect of handedness on the animal motion path to a target is modeled.

Results

It has been suggested by von Kármán & Burgers¹¹ and echoed by Lighthill¹², that fish swimming (due to their caudal fins) is a self-regulating process that can occur only at transitional Reynolds numbers; a reverse Kármán jet is present and optimal efficiency is a measure of this process. Swimming and flying animals cruise by flapping their caudal fins (or pectoral fins/wings) in a narrow St range (0.20 to 0.40). Within that range, each species selects a more or less characteristic value of St. When all flapping and flow parameters in St are held to high precision (considered below), nonlinear oscillators that describe the fluctuation in (thrust) force production to the lowest order produce characteristic locked-in maps (Fig. 3). Different vortex-based swimming and flying animals with their characteristic Re_c and St select transitional regimes of wake having typical lock-in phase maps that also define the trajectories they are capable of undertaking. (A phase map is said to be “locked-in” if each cycle of the fin's oscillation produces initial conditions that produce the same phase map over the next cycle.) Laboratory measurements show that the constancy of St is a tuning process⁸. Put simply, each vortex-propelled animal is constantly broadcasting its detailed motion histories to friend and foe alike. The process is deterministic but not precisely predictable due to sensitivity to initial conditions.

Figure 3

Theoretical modeling of the sensitivity of force production to the precision of Strouhal number showing the loss of lock-in when St is changed at the third decimal place.

(a − o) U = 0.60 m/s, Re_c = 39,684. Flapping frequency: f = (a) 0.39 Hz, (b) 0.40 Hz, (c) 0.41 Hz, roll amplitude , pitch amplitude θ₀ = (a) 21°, (b, c) 22°; Strouhal number St = (a) 0.2109, (b) 0.2163, (c) 0.2217; f = (d) 0.49 Hz, (e) 0.50 Hz, (f) 0.51 Hz; , θ₀ = (d) 26°, (e) 27°, (f) 28°; St = (d) 0.2649, (e) 0.2703, (f) 0.2757; f = (g) 0.59 Hz, (h) 0.60 Hz, (i) 0.61 Hz; , θ₀ = (g, h) 32°, (i) 33°; St = (g) 0.3190, (h) 0.3244, (i) 0.3298; f = (j) 0.66 Hz, (k) 0.67 Hz, (l) 0.68 Hz; , θ₀ = (j, k) 36°, (l) 37°; St = (j) 0.3568, (k) 0.3623, (l) 0.3677; f = (m) 0.74 Hz, (n) 0.75 Hz, (o) 0.76 Hz; ; θ₀ = (m) 40°; (n, o) 41°; St = (m) 0.4001, (n) 0.4055, (o) 0.4109. Twist amplitude and phase are held the same in (a − o).

The tuning process can be understood in the framework of nonlinear oscillators⁸. It is known that to leading-order approximation the vortex shedding instability of a rigid cylinder can be described as a van der Pol oscillator¹⁵. This oscillatory description has been extended to a cylinder undergoing vortex-induced vibration¹⁶ and it has been suggested that the description might also apply to thrust-producing flapping wings¹⁷. Experiments⁸ with flapping fins show that the lowest order of thrust force fluctuation can be described by the equation and the maps of force fluctuation versus its time (t) derivative systematically vary with Re_c (Fig. 2a). Here, , where roll pitch flapping frequency () is expressed as flapping amplitude , is the fluctuation in force, is the amplitude of and G ( = 0.02) and T ( = 0.5) are constants; the subscript o denotes amplitude, is the phase difference (90° ± 10° due to optimal fin twisting) and R_avg is the radial distance at which the disk blockage area created by the fin's spanwise flapping can be divided equally (the net fin force at any instant t can be assumed to act at this roll distance at the point on the fin where the hinge is pitched—this being at a distance of c/3 from the leading edge)^7,18; is a bias angle applied to the pitch angle for yawing. The referenced experiments were carried out for a realistic (in terms of planform, fin section, aspect ratio and Reynolds number), penguin-scale, hinged fin that is being optimally twisted while also rolling and pitching (optimal twisting makes the leading edge vortex uniform along the span and the Coriolis force due to the rolling of hinged fins pins the vortex onto the fin¹⁹). In twisting and flapping fins, both the efficiency and the product of the efficiency and the thrust coefficient reach high values in narrow combinations of St and ⁸.

Precision of tuning of force oscillators

The following theoretical analysis can be carried out to understand how precisely swimming and flying animals are tuning their characteristic Strouhal number for maximization of efficiency at a given Reynolds number. This analysis leads to an internally consistent deterministic oscillatory modeling of actuators, sensors and controllers.

In a fin optimally twisted along the span⁸, the force fluctuation map () is given by the self-regulation equation . The sensitivity of the map's lock-in to the precision of St can be determined. This precision affects both the tuning and efficiency of the oscillator and indicates how low the structural damping is¹⁶. Consider the lowest order fin force fluctuation maps. Figure 3 shows examples of maps of () where St is varied nominally from 0.21 to 0.40 (note in the captions that St and θ_o are coupled⁸). Time increases from blue to red in the figures. Sharks, dolphins and large fish have St near 0.30 (approximately), insects are near 0.28, bats have St ≥ 0.30 and birds have St near 0.20⁹. (For the large animals, Re_c should be ≥ 40,000, where we expect stable shed vortex-vortex interaction and effects on fin force⁸ and acoustic radiation—see Fig. 2a.) Therefore, even within the narrow St range of 0.20–0.40, each swimming and flying animal is built for preferred values of St and, roughly speaking, birds are near 0.20 while the large swimmers are near 0.30.

In Fig. 3, for the same value of Re_c and within the range 0.21 to 0.40, St is varied with a precision of four decimal places slightly below and slightly above the nominal St values of 0.21, 0.27, 0.32, 0.36 and 0.40. The maps lock in at those values in the (b, e, h, k, n) portions of Fig. 3 only when St is held to at least three-decimal-place precision. The parameters have to be held to high precision for perfect tuning. With St, the lock-in map varies. Lock-in occurs when the same initial condition is produced in each half of flapping. We predict that each swimming and flying type of animal, therefore, is likely to have its own characteristic locked-in map where hydrodynamic efficiency reaches its maximum value and structural damping is at a minimum. In view of this orderliness, it would not be surprising if swimming and flying animals in fact hold their St to an accuracy of greater than or equal to four decimal places—a remarkable feat.

Similarity of unsteady force field and sensor response

Near the onset, reverse Kármán vortex shedding acts like a supercritical Hopf bifurcation and the van der Pol, Stuart-Landau (SL) and Ginzburg-Landau (GL) oscillators are equivalent^15,20. The GL model is applicable to a band of wave vectors near the bifurcation point. We model the higher order force fluctuations using the SL oscillator, which applies to a single wave vector. If the fin and the wake are uncoupled, the SL equation for the evolution of wake circulation A is given as , where A* is the complex conjugate. Here, σ and λ are complex constants of the wake; see Albarède & Monkewitz¹⁵ for the estimation procedure. Assume that the downstream circulation affects the angle of attack (), which alters the force . The angle α_g is the geometric angle of attack obtained from the forward velocity and spanwise fin flapping velocity (see Methods). If the fin and the wake are coupled, the wake evolution is also dependent on lift (L) evolution as and and, , where the coefficient scales the coupling between the wake and the fin. To account for fractals of unsteadiness, we assume that higher-order equations include lower-order equations (forces are affected by their higher-order gradients) The model results are compared with measurements in Figs. 4a and 4b at identical Reynolds numbers and fin flapping parameters, including optimal twisting (see Methods for the method of calculation). Twist amplitude and phase have been accounted for at R_avg; each⁸ is 10°. They compare well.

Figure 4

Similarity of force production fluctuation and acoustic sensor response.

(a) Measurements of fin force fluctuation maps⁸ (N-N/s) and (b) second-order Stuart-Landau equation model (N-N/s) of fin force fluctuation in optimally twisted hinged fin at Re_c = 49,121; (c) model of acoustic combined hydrophone-accelerometer sensor response b for W_x = W_y = 1, W_p = 1/2, θ_s = π/8; (a) The fin force measurements are in the range 39,923 ≤ Re_c ≤ 70,895 where the map is stable. Time increases from blue to red in (a).

Figure 4b depicts a locked-in response for the second-order model. While each cycle is the same, each half of the cycle does not precisely match the other half, giving rise to the double loop centered near (0.5 N, 0 N/s). One half of the cycle gives rise to the initial conditions that produce the shape of the other half of the cycle and vice versa. This difference between the half-cycles is related to the initial conditions—an initial condition with higher magnitude gives rise to a larger difference between the half-cycles.

The notable difference between Figs. 4a and 4b is that in the experiments St is nominally 0.30, while in the model it had to be taken to be 0.2999075 to lock in the loop. If St = 0.3008, the two halves don't lock in perfectly and they slightly oscillate (see Animation 2 in the SI). Therefore, the flapping fins are nonlinear oscillators, where the fin and the shed vortices are coupled. It is known that swimming and flying animals cruise at St numbers of 0.20 to 0.40^9,10. From the above modeling, it is concluded that they cruise near bifurcation points where the conditions are slightly nonlinear and slightly unstable. An unstable platform is amenable to maneuverability. Due to its self-regulating nature, the platform will reject disturbances (Animation 1), making it robust.

We now explore another property that helps homing, namely, the relationship between the sensors—more specifically, the relationship between the combined hydrophone-accelerometer sensor and the actuator. We suggest that the lateral line sensors are not just hydrophones but are vector sensors because they combine hydrophones with tri-axis accelerometers and essentially solve Euler and wave equations.

Consider the response () of a single acoustic (combined hydrophone-accelerometer) sensor (θ and are the polar and azimuthal angles, respectively and the subscript s is for steering). For a unit velocity V, applying equation (2.29) of Psaras²¹ to his equation (2.24) yields the expression where W_x, W_y and W_z are the weighting factors for the accelerometers in the orthogonal x, y and z directions, respectively. These weights have been made independent of each other, a generalization of Psaras' equation (2.29). The weight for the pressure sensor is given by W_p and it is understood that the “pressure-velocity” V_p = P/ρc is equal to the velocity V. The equation above yields a three-dimensional response in θ and , dependent upon the “steering angles” θ_s and . The “null angle” θ₀ is the angle in the domain at which b = 0 (in Fig. 4c, θ is zero in the vertical axis and positive in the clockwise direction; the steering angle is the angle θ where the maximum absolute value of the response b occurs.)

The above trigonometric relationship can be simplified to include only the information for the plane , such that Restricting to the condition where θ₀ − θ_s = π, at which point the null angle is directly opposite the steering angle, yields Depending on the remaining weights W_x, W_y and W_p, the resulting limaçon may be given a dimpled, cusped (cardioid), or looped character (see Part C of the SI for the results when θ_s = 0) as in force fluctuation measurements⁸ with Re_c. The result for θ_s = π/8 is shown in Fig. 4c and is compared with measurements of force fluctuation. The maps in Figs. 4a, 4b and 4c are similar. The map is slightly slanted to the right in Fig. 4a. Figure 4c reproduces the slant in the null-steering angle. (The force maps and the sensor response can be three-dimensional.) Therefore, the sensor response is similar to the bifurcation point response of the force actuator.

Modeling of animal motion path using orthogonal olivo-cerebellar oscillators

We now explore the relationship of animal motion path, which is the result of force actuation and sensing, to olivo-cerebellar dynamics. For an inferior-olive neuron i, the states are given by , , and and the nonlinear functions are given by and ²². Here, z_i and w_i are associated with sub-threshold oscillations and low-threshold (Ca-dependent) spiking and u_i and v_i represent the higher threshold (Na⁺-dependent) spiking. The constant parameters and control the oscillation time scale; I_Ca and I_Na drive the depolarization levels; and k sets a relative time scale between the uv- and zw-subsystems. The Ca oscillator can be written as , where F is a cubic polynomial function, k is a constant and the extra-cellular impulse I_exti(t) = 0¹³. This control oscillator is similar to the fin force fluctuation oscillator mentioned earlier, where is non-zero and is the forcing term due to roll, pitch and twist oscillation.

The states of two inferior-olive (IO) neurons were calculated using an analog circuit¹³ whose validation is shown in Part B of the SI. Figure 5a shows the flight path of a trained brown bat (named “Poe”) through a maze of chains in a room as it approaches an insect offering²³. Figure 5b shows an example of the map of states z1 and w2 from two IO analog neurons—one strong and one weak (they have the large and small limit cycles, respectively, shown in Figs. S2d and S2e). The maps have a basic similarity—less curved paths extending over the room, with large loops to one side. The paths do not repeat, which may aid avoidance of dynamic obstacles. Two other bats (named Frosty and George) have tracks²³ similar to those in Fig. 4a—which are due to Poe—consisting of segments of similar, mainly very long, less-curved and rounded paths.

Figure 5

Modeling of bat trajectories using orthogonal olivo-cerebellar oscillators.

(a) Trajectories of the brown bat (named “Poe”) in the horizontal plane approaching an insect in a room filled with hanging chains²³. The red circle denotes the location of a chain that was removed and then put back to see the effect on the trajectories. (b) Modeled trajectories using two olivo-cerebellar Ca oscillators.

Figures 4 and 5 show that in animals with flapping fin actuators, the actuator, sensor and controller follow similar dynamical system relationships.

Handedness and homing

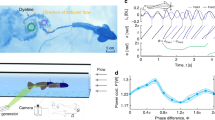
The motion of a 1-m-scale platform propelled by a pair of flapping pectoral fins was modeled (see Part D of the SI for details). Two hydrophones were placed at the mid-span locations. The initial location and orientation of the platform with respect to a moving target were chosen arbitrarily. The target is an acoustic source that the platform tracks and approaches. The flapping fin force is known to be proportional to the square of the flapping fin frequency if the roll and pitch amplitudes and the phase difference between roll and pitch are held constant⁷. The flapping frequency versus range relationship is assumed to be similar to the characteristic chirp pulse intensity versus range of bats approaching target insects²⁴. This intensity trend decreases as the target is approached (Fig. S6 in the SI). (The drop in echo location pulse amplitude as target distance is halved is 6 − 6.5 dB in bats²⁴ and 6 dB in free ranging dolphins⁶). Initially, the platform loiters aimlessly with random speed and orientation, while the mobile target is quiet. Then, the target turns on the noise source at a random instant (note the hook in the starting trajectory of the platform). The subsequent trajectories of the platform and the target are shown in Fig. 6 when the target has a lemniscates path of arbitrary frequency. The platform constantly ranges the target sound source. In one case, the two pectoral fins of the platform have equal span (even-handed). In the other, one of the spans is short. In Fig. 6, the results for even-handedness and 10% right-handedness (left hand is 10% shorter) are compared. The target is not reached even in 250 s when the fins have even-handedness, while it is reached in 170 s when the fins have 10% right-handedness. The 10% right-handed case reaches the target earlier by taking a shorter path. (See Fig. S8 of the SI for the case when the target is static—heading and bearing oscillate as the target is reached, unlike in the even-handed case.) Handedness alters the global path. If its degree varies, it can be a means for path control to accommodate an unstructured environment.

Figure 6

Modeling of the effects of handedness on homing.

(a, b): Position of the platform (blue) and the target (red) when the target has a lemniscates trajectory and the source is (a) even-handed, or (b) 10% right-handed. The platform is indicated by a triangle. The contours indicate constant sound pressure level (SPL) around the source; the SPL changes versus time with the motion of the source. The indicated contours pertain to the last location of the source. (c, d): Range to target with time for even-handedness (c) and 10% right-handedness (d).

Discussion

The present results indicate that fish lateral line sensors are combining the measurements of the sound pressure level and fluid acceleration vector to calculate the direction and range of other vortex-propelled animals in their surroundings. While the fluctuations in the wake vorticity due to the reverse Kármán vortex trains produce pressure waves that help to close the loop between the wake and the fin Kutta conditions²⁵, these pressure waves also broadcast the presence of the flapping fin source and its Reynolds number to both friend and foe, who use the information for ranging. In open waters, smaller swimming animals are most vulnerable due to the cumulative threats from larger animals, who listen to the acoustic broadcast. We speculate that in the face of a pursuer, small fish form a school using their lateral lines and vision. By forming a school of parallel individuals (called polarization)¹⁴, the smaller animals synchronize their acoustic radiation and try to appear larger (lateral lines allow fish to maintain a larger distance in a school than vision does and fish use both of these senses to school). Other strategies employed by small fish include hiding in background acoustic clutter near the bottom or surface to mask their weak acoustic radiation.

The force fluctuation and sensor response maps for W_x = W_y = 1, W_p = 1 are topologically similar to the central bulb of the Mandelbrot fractal set. Fractals appear on the central bulb of the force maps when higher harmonics in the time series are included⁸. Bats use higher chirp harmonics for target detection in ground clutter²⁶. Similarly, the fractals of the noise map can be used by a fish to detect smaller fish in the cluttered bottom.

Handedness may be likened to the forked tongues of snakes, which are stereoscopic olfactory sensors for source ranging. The potential exists that the fast C-start escape response to an alarm in fish may be handed. The external pinnae of vertebrates such as cats, dogs and bats are obliquely truncated which raise the maximum pressure gain above that of a horn truncated normally with the same minimum throat-to-mouth distance²⁷. In addition, particularly at low frequencies, the oblique truncating bends the axis of maximum acoustic response away from the geometric axis. Thus, inclining the pinnae differently, a differential sensing sensitivity between the left and right ears can be created to control handedness.

Further, the following observations suggest a link between (1) the macro-scale animal acoustics for detection of other fish and avoidance of predators and (2) the micro-scale ciliary fluid mechanics and ionic mechanisms in gene expression; this link leads to handedness in animals. First, as compared to their sighted counterparts, blind Mexican cave fish²⁸ have larger neuromasts protruding into their boundary layers. Some blind fish population from the Granada Caves have asymmetrical degeneration of the eyes, where one eye is normal, while the other is slightly reduced in size and complexity²⁹. Zebrafish neuromasts have clusters of approximately 20 μm long cilia protruding from their skin pores, allowing the external flow to stimulate the hair cells. Cilia are now seen as interconnected molecular machines with many components of signaling cascades³⁰. Second, the ability of cilia to produce unidirectional flow plays a key role in the mechanism of how left-right symmetry is broken in the placement of internal organs and associated vasculature in mammalian early embryos³¹. This unidirectional flow drives asymmetries in gene expression and Ca²⁺ signaling in cells³².

The nonlinear control basis for the paths in Fig. 5a shows that the proverbial straight crow's flight is a fiction and that swimming and flying animals are built for chaotic nonlinear trajectories, which allows them to circumvent unfamiliar obstacles. Our modeling reproduces the observations of the experiments²³; namely, it shows how the bats undertake a global change in path, cycle to cycle, to accommodate smaller scale changes in the structure of the environment. The chaotic nature of the z-w oscillator makes this possible by utilizing two oscillators along two orthogonal axes, the larger oscillator making global changes in the path and the smaller oscillator making local smaller scale changes. The paths are smooth and there are no kinks in any higher derivatives.

In robotics, by incorporating handedness with the nonlinear, oscillatory co-directivity of sensors, actuators and controllers, one would reproduce animal-like gait and homing ability. Rapid homing due to handedness would be beneficial in time-critical robot-assisted rescue missions. In another application, handedness could shorten the data search path in large networks.

Because homing is important to life with regard to food and reproduction, the present work shows an origin of handedness independent of social pressure, although we do not see any advantage in right-handedness over left-handedness. However, the bat path simulations show that a preferred type of handedness is rooted in weak-strong oscillator interaction in membrane ion-flow, which the actuators and the sensors mirror (the weak-strong ratio of state levels is 0.03 in Fig. 5b; see Fig. S9 and Animation 3 in the SI for an example of the interaction when the state level ratio is 0.001). Near the Hopf bifurcation, the weak oscillator provides a tiny bias to sway the system preferentially to one of the branches, giving rise to macroscopic handedness.

The motion of vortex-propelled animals has been modeled using analytical theories of nonlinear oscillators. In particular, it has been shown that handedness in fish/fish-like interaction accelerates homing of the pursuer on the target; handedness removes ambiguity near a target and acts as a useful bias. The fish habitat emerges as a ”cocktail party filled with cacophony.” And yet, inexorably, both the pursuer and the target are cognizant of each other through the din. While handedness is ubiquitous, to obfuscate detection and capture, the target animal employs numbers, schooling¹⁴ and acoustic clutter to live for another day, while the pursuer carries out complex harmonic signal processing²⁶ in an attempt to close the deal.

Methods

Stuart-Landau modeling of the flapping fin forces

The function f(A) appearing in the main paper has been assumed to be linear such that

where S and A_pl refer to the fin's span and planform area, respectively. The coefficient scales the contribution of the wake to the angle of attack and is understood to be a constant between 0 and 1. The fin forces can be assumed to be acting at a distance of R_avg from the roll axis⁸. Considering the radii at the root and tip of the fin, the velocity U(t) is the instantaneous velocity at

where c and x₀ represent the chord length and the distance, respectively, from the leading edge to the pitch axis ( = c/3); x is the forward axis; y is the spanwise axis; and θ is the temporal pitch angle.

The function

where

Here, T is the thrust and α is the temporal angle of attack at the span of R_avg. The coefficient κ is the slope of the C_L versus α curve at α approaching 0, which is taken from our past non-flapping single fin measurements⁷. St is the Strouhal number of the flapping fin obtained from the flapping frequency, roll excursion amplitude at R_avg and forward fin velocity⁸.

Note that the angle of attack that will be applied to the lift model in equation (7) will be our estimate of the “true” angle of attack α = α_g + α_wake, where α_wake = f(A), per the main paper (angles a and a_g are depicted in Figs. 7a and 7b, respectively).

Figure 7

Schematics of angles of attack showing fin-wake coupling.

(a) Physical origin of the geometric angle of attack α_g as it appears to a fixed observer. (b) Angle of attack α in fin-centered coordinates. Circulation in the wake yields α = α_g + α_w; if the contribution of the wake is ignored, α = α_g.

The second-order model with results shown in Fig. 4b was run using the parameters given in Table 1 ( is the roll amplitude; θ₀ is the pitch amplitude; the subscript t is for twist; ψ is the phase difference between roll and pitch; the subscript r is real and the subscript i is imaginary).

Table 1 Summary of parameters used in the Stuart-Landau modeling of flapping fin forces

The wake frequency (Strouhal number) for a non-flapping foil ω_wake is derived from a relationship in Yarusevych et al.³³,

The width of the wake d* has been approximated here by the expression

where α_g,max = 12.97° is the largest instantaneous geometric angle of attack seen by the fin. Note that in this work, we have used a slightly higher value of St_wake (0.1752) based on our interpretation of Yarusevych et al.'s Fig. 21, in which the data “scatter” for Re_c < 130,000 appears to be non-random, with higher angles of attack being associated with higher St_wake.

The amplitude of circulation oscillation for a non-flapping foil A₀ is related to the amplitude of lift oscillation for a non-flapping foil L₀ by

where L₀ has been estimated from our experimental data⁸, such that

Experimental data source

Fig. 1b: sourced and adapted from refs. 5 and 6.

Fig. 4a: sourced from ref. 8.

Fig. 5a: sourced from ref. 23.