Abstract
This paper delves into the investigation of the COVID-19 dynamics within a host using the Target-Latent-Infected-Virus (TLIV) model, presenting a fresh approach compared to previous studies. Our model introduces a latent class and explores sensitivity analysis, aspects that have received limited attention in prior research. A significant contribution of this study is the analysis of both local and global stability of equilibrium states, subject to specific sufficient conditions based on the basic reproduction number \(R_0\). By examining these stability properties, we aim to gain insights into the factors underlying variations observed in the findings of different studies. Additionally, we identify the death rate of infected cells as the parameter most susceptible to influence in our model. To minimize its impact and facilitate recovery, it is crucial to implement appropriate medical therapies and consume immune-boosting foods. Some computer simulations are carried out to strengthen the theoretical results.
Similar content being viewed by others
Introduction
The novel coronavirus SARS-CoV-2, emerged as a global health crisis in history that has been uncovered by the year 2020. In Wuhan, Hubei Province, China in December 2019, coronavirus (COVID-19) disease was first reported1. The virus affected more than two hundred countries and killed millions of people according to the World Health Organization. The infection can be controlled by physical social distancing, self-isolation at home, face masks, hand-washing, and surface cleaning2,3. Several countries have proposed strict social distancing and lock-down regulations to stop the spread of the virus. It is primarily transmitted through respiratory droplets when an infected individual coughs, sneezes, talks, or breathes. The virus can also spread by touching contaminated surfaces and then touching the face. Common symptoms of COVID-19 include fever, cough, fatigue, shortness of breath, and loss of taste or smell, although asymptomatic cases are also prevalent4.
The disease severity ranges from mild to severe, with some cases progressing to acute respiratory distress syndrome and multi-organ failure, particularly in vulnerable populations such as the elderly and those with underlying health conditions5,6. Rapid and widespread transmission led to the declaration of a pandemic by the World Health Organization (WHO) in March 2020, prompting the implementation of various control measures like social distancing, mask-wearing, and vaccination campaigns7. Efforts to combat the disease have also focused on testing, contact tracing, and the development and distribution of vaccines. Understanding the basic details of COVID-19 is crucial for effectively managing and mitigating its impact on public health systems and communities worldwide.
Mathematical epidemiological models play a crucial role in understanding the dynamics of infectious diseases, providing valuable insights into how these diseases spread within populations. These models capture the rapid fluctuations in the number of infected individuals, serving as the fundamental principle of mathematical modeling. A wide range of mathematical models that describe various types of diseases can be found in the literature8,9,10,11,12,13,14. Numerous studies with many intriguing mathematical models that have examined the dynamic behavior of SARS-CoV-2 can be found in2,15,16.
Within the human body, biological mathematical models offer valuable insights into the complex dynamics of infectious diseases at an individual level. These models integrate principles from both biology and mathematics to depict the interplay between pathogens, the immune system, and host cells17. By considering factors such as viral replication, dynamics of immune responses, and the effects of treatments, these models facilitate a deeper comprehension of disease progression and contribute to informed therapeutic interventions18.
Few research papers could predict the dynamics of COVID-19 disease accurately and according to World Health Organization, dozens of vaccine candidates are in clinical research, and about ten vaccines are authorized for public use19,20. Clinically, there is no effective treatment that can remove the virus from the human body, however, the available treatments help like Ebola, Influenza, and SARS-CoV-1.
It is known that several works have focused on forecasting the number of infected individuals in populations21,22. Forecasting for COVID-19 is exceedingly difficult and has failed in many papers because of the type of mathematical models, missing data, and/or the random behavior of this virus23. We think it is time to study the dynamics of COVID-19 within-host instead of between the human populations.
Within-host COVID-19 model
Based on current data, it is estimated that around 80% of COVID-19 cases are classified as mild to moderate, and individuals in these cases typically experience a full recovery from the infection24. Previous research has indicated that the humoral response, involving the production of antibodies, to SARS-CoV-2 infection is commonly observed in individuals who have been infected. The level of antibodies, specifically the anti-SARS-CoV-2 IgG titers, has been strongly linked to the extent of virus-specific CD4+ and CD8+ T cell responses in the bloodstream25. However, it should be noted that most samples of convalescent plasma, collected from individuals recovering from COVID-19, did not exhibit high levels of neutralizing activity. Furthermore, only a small number of individuals who were analyzed showed the presence of rare antibodies that possess potent antiviral activity against specific viral proteins26.
The angiotensin-converting enzyme 2 (ACE2) receptors present on the surface epithelial cells are bound by the SARS-CoV-2 virus. These cells, which express ACE2, are considered susceptible to viral infection and are referred to as target cells in mathematical models. The distribution of these target cells varies notably across different sections of the respiratory system, with the lungs having the highest density, followed by the nose, and finally, the tissues of the trachea/bronchi. Consequently, COVID-19 patients often experience pneumonia, making it a relatively frequent occurrence27,28.
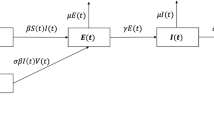
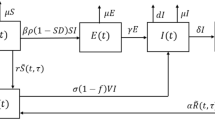
Our proposed model in this paper comprises four variable quantities, the susceptible targeted cells, T(t), latent cells, L(t), infected cells, I(t), and free virus particles, V(t). The model assumes that there is a constant of regeneration \(d_1 T(0)\) susceptible targeted cells. These cells are infected by free virus particles with a bilinear incidence rate \(\beta T(t)V(t)\) and these infected cells produce with a rate p free virus particles. Parameters \(d_1, \, d_2, \, d_3,\) and \(d_4\) are the death rate of susceptible target cells, latent cells, infected cells, and free virus particles, respectively. Latent cells on average span 1/k units of time in L class and then join the infected class of cells. It should be noted that \(d_1\) is a natural death rate or natural clearance rate while \(d_2, \, d_3\) and \(d_4\) are a combination of the natural clearance rate and the role of the immune system in the elimination of these cells.
Our work presents a novel mathematical model that incorporates latent class analysis to describe the dynamics of COVID-19 within the host. Unlike previous studies that focused solely on estimating the basic reproductive number29, or analyzing the stability of equilibrium states30, our model delves deeper into the impact of various parameters on the system. By conducting sensitivity analysis, we have identified the death rate of infected cells as the most sensitive parameter in our model. This finding sheds light on the critical role this parameter plays in shaping the dynamics of COVID-19 infection and highlights its potential implications for disease progression and management strategies.
Authors in29,30 have studied the viral kinetics of COVID-19 without latent class of cells, we consider the mathematical within-host model in the form
The originality of our model lies in the inclusion of a new class, namely the latent cells, to capture the dynamics of COVID-19 within the human body. Within this class, individuals or cells have been exposed to the disease but have not yet reached the infectious state. The duration of this latent period, determined by the delay parameter, signifies the time it takes for individuals or cells to become infectious. This approach is applicable to more general fractional systems, see31.
In the traditional model, only the susceptible, infected, and viral load compartments were considered. However, by introducing the latent class, we aim to provide a more realistic representation of the disease progression. This addition accounts for the incubation period during which the virus replicates within the body before symptoms become apparent. By incorporating the latent class, our model captures an essential aspect of the disease phenomenon, enhancing its accuracy and predictive capabilities. It can serve as a valuable tool for studying the effectiveness of interventions and informing public health strategies aimed at controlling the spread of COVID-19.
Here are the model assumptions:
-
1.
In COVID-19, the respiratory system’s cell population remains constant due to the slow turnover of respiratory epithelial cells.
-
2.
\(d_1T(0)\) is assumed to be a constant of regeneration of cells.
-
3.
Once cells recover from the infection and become immune, the model assumes that they remain immune indefinitely.
-
4.
Cell variations in susceptibility are not considered.
-
5.
During the latent period, cells are considered non-infectious or have a low probability of transmitting the disease to other cells.
-
6.
There are no major changes in the characteristics or behavior of cells within the latent class during the modeling period.
Graph of the system
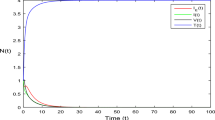
By performing parameter estimation in a similar way to29,30, using the Monte Carlo Markov Chain (MCMC) method, and in light of the chest radiograph score data, the estimated values of parameters are \(T(0) = 50, \, \beta = 1, \, d_1 = 0.2, \, d_2 = 2, d_3 = 1.1, \, d_4 = 3, \, k = 1.7\) and \( p = 0.05\). In this scenario, the graph of our model (1) can be sketched in Fig. 1 in 30 days.
Basic properties of the system like the nonnegativity and uniform boundedness of the solution are shown in the next section. The equilibrium states of the model and the basic reproduction number are provided in Section “Equilibrium states and the basic reproduction number”. Local and global stability of the equilibrium states \(E_0\) and \(E^*\) with some computer simulations are shown in Section “Extinction and persistence”. Viral kinetics of the COVID-19 model using sensitivity and elasticity analysis of \(R_0\) towards the effective parameters in the model are shown in Section “Sensitivity and elasticity of \(R_0\)”. Conclusions and some future works are devoted to Section “Conclusion and further directions.
Nonnegativity and uniform boundedness of the solutions of (1)
In this section, we study the nonnegativity and the uniform boundedness of the solutions of the within-host model (1) with respect to the initial conditions
The next theorem proving nonnegativity and uniform boundedness in the mathematical model of cell population dynamics ensures valid interpretations and prevents unrealistic predictions, supporting reliable analysis and decision-making in cell biology and related fields.
Theorem 2.1
Assume that the initial values (2), then all solutions of (1) are nonnegative and uniformly bounded.
Proof
The first equation of model (1) is
Using the integrating factor
we have
i.e.,
Similarly,
Regarding the boundedness of the solutions of (1), the total population of cells \(N(t) = T(t)) + L(t) + I(t)\), where
Assume that \(d = \min \lbrace d_1, d_2, d_3\rbrace \), then
and
Consequently, all solutions of (1) with respect to (2) are bounded in a biologically feasible region
Clearly, the number of free virus particles is also bounded at any time t. \(\square \)
Equilibrium states and the basic reproduction number
Equilibrium states of this model satisfy the following algebraic equations
Clearly, we have two equilibrium states at most, the infection-free equilibrium state \(E_0 = (T_0,L_0,I_0,V_0) = (T(0),0,0,0)\), and a positive endemic equilibrium state
Using the method of Next Generation Matrix (NGM) used by32, we calculate the basic reproduction number \(R_0\). The three compartments of infection are
where
The Jacobians of \({\textsf{F}}\) and \({\textsf{V}}\) are
Then
The basic reproduction number \(R_0\) is defined as the spectral radius of \({\textsf{F}}_0 {\textsf{V}}_0^{-1}\), consequently
Then for \(R_0 >1\), there is a unique positive equilibrium that can be written again in the form
Extinction and persistence
In this section, we shall perform the stability analysis, in terms of the basic reproduction number \(R_0\), we study the extinction and the persistence of the disease inside the human body by focusing on the local and global stability of \(E_0\) and \(E^*\). Evaluating the Jacobian matrix J at the equilibrium states, the LaSalle-invariance principle and the Routh-Hurwitz criterion33 are used for investigating the local stability of these equilibrium states. Introducing appropriate Lyapunov functions around the equilibrium states is very helpful in investigating the global stability of these states34.
Extinction
Theorem 4.1
If \(R_0 < 1\), the infection-free equilibrium \(E_0\) is locally asymptotically stable. And if \(R_0 \le 1\), then \(E_0\) is globally asymptotically stable.
Proof
The Jacobian matrix for the right hand side of (1) is
Evaluating J at the infection-free equilibrium \(E_{0}\)
Let \(\lambda _i\) be the eigenvalues of this matrix for \(i = 1,2,3,4\) such that
If \(R_0 < 1, \, \prod _{i=1}^{4} \lambda _i > 0\), then the infection-free equilibrium state is locally asymptotically stable. For global stability of \(E_0\), choose the Lyapunov function in the form
where
Then \(\frac{d{\mathcal {V}}}{dt} < 0\) if \(R_0 < 1,\) and \(\frac{d{\mathcal {V}}}{dt} = 0\) if only \(V = 0\) or \(R_0 = 1\). According to the LaSalle-invariance principle34, the equilibrium state \(E_0\) is globally asymptotically stable. \(\square \)
The theorem’s implications are significant for disease control strategies, as it offers insights into conditions favoring infection eradication and emphasizes the significance of minimizing the basic reproduction number (\(R_0\)) to prevent outbreaks and ensure the well-being of the cell population.
The Euler method scheme is utilized for simulating the within-host COVID-19 model35. This numerical approach partitions time into small intervals and estimates variable changes within each interval. Through the iterative application of this scheme, the model can simulate disease progression over time, considering parameters such as viral replication, immune response, and cell death rates. Other numerical schemes have also been employed to simulate COVID-19 and other various disease models within-host and between individuals36,37,38.
Using the initial values \((T(0),L(0),I(0),V(0))=(50,15,15,3)\) and the parameters \(\beta = 2, \, d_1 = 0.9, \, d_2 = 1.8, \, d_3 = 3.1, \, d_4 = 4.5, k = 0.07\) and \(p = 0.9\), we can see the convergence of the trajectory of the solution to the infection-free equilibrium state. Infected cells, Latent cells, and free virus particles will be eliminated from the human body for \(R_0 < 1\) as shown in Fig. 2a. The relations between target cells and the other compartments are shown by the phase planes in Fig. 2b–d. The disease dies out within the human body for \(R_0 < 1\).
Persistence
Theorem 4.2
The positive endemic equilibrium \(E^*\) is locally asymptotically stable and globally asymptotically stable if \(R_0 > 1\).
Proof
Evaluating J at the positive endemic equilibrium implies
The characteristic equation is
Now, for \(R_0 > 1,\)
and
Then according to the Routh–Hurwitz criterion, the positive endemic equilibrium \(E^*\) is locally asymptotically stable. Regarding the global stability of \(E^*\), choose the Lyapunov function
Then
Using the equations
implies
As the arithmetic mean is greater than or equal to the geometric mean, then \(\dot{{\mathcal {V}}} < 0\) and \(\dot{{\mathcal {V}}} = 0\) only if \(S = S^*, L = L^*, I = I^*\) and \(V = V^*\). Then according to the LaSalle-invariance principle, the positive endemic equilibrium \(E^*\) is globally asymptotically stable. \(\square \)
Using the same initial values of the numerical simulation in Fig. 2a, and the parameters \(\beta = 1.3, \, d_1 = 0.6, \, d_2 = 0.8, \, d_3 = 2.1, \, d_4 = 4.5, k = p = 0.9\), the disease persists within the human body. Figure3a shows the convergence of the trajectory of the solution towards the positive equilibrium state \(E^*\) for \(R_0 > 1\) with some phase portraits that show the behavior of the target cells with each compartment in Fig.3b–d.
Sensitivity and elasticity of \(R_0\)
The basic reproduction number \(R_0\) quantifies the average number of secondary cases generated by the introduction of a disease into a susceptible population. It is a vital measure for assessing the potential for disease transmission39. Many papers have used optimal control strategies and sensitivity analysis of many disease models including COVID-19, see40,41. In our study, we examine the impact of the basic reproduction number \(R_0\) on the dynamics of infected cells and free virus particles over a span of six weeks, as illustrated in Fig. 4. During this time interval, we observe that higher values of \(R_0\) lead to a greater peak in the number of infected cells and free virus particles. This suggests that a higher \(R_0\) is associated with a more pronounced spread of the infection within the host. Furthermore, in Fig. 5, we present surface plots that depict the relationship between \(R_0\) and the various parameters incorporated into our model. These plots allow us to visualize how changes in these parameters influence the value of \(R_0\), providing insights into the factors that impact the transmissibility and progression of the infection.
In order to gain insights into the factors that have the most significant impact on the number of infected cells and free virus particles, we conducted a sensitivity analysis. This analysis allowed us to determine the sensitivity of the basic reproduction number \(R_0\) with respect to a specific parameter \(\omega \) by calculating the derivative \(\frac{\partial R_0}{\partial \omega }\). By plotting the dynamics of infected cells I(t) and free virus particles V(t) for various values of the infection rate \(\beta \), we observed an interesting trend: when the infection rate was low, the number of infected cells and free virus particles exhibited a slower rate of decrease. Additionally, we found that the sensitivity of parameter \(d_2\) and the latent period \(\frac{1}{k}\) have a similar impact to \(\beta \), which is demonstrated in Fig. 6.
The sensitivity analysis of within-host model parameters involves examining the impact of variations in parameters on the model’s output. By systematically altering these parameters, we can assess their influence on key model outputs such as viral load, disease progression, and the effectiveness of interventions or treatments.
The death rate of free virus particles \(d_4\) and the rate of free virus production p exhibit similar effects on the number of infected cells I(t) and free virus particles V(t), particularly impacting the abundance of free virus particles. However, the parameter that demonstrates the highest sensitivity to both I(t) and V(t) is the death rate of infected cells \(d_3\). As we mentioned previously, this death rate represents a combination of natural clearance mechanisms and the role of the immune system. Therefore, it becomes essential to consider treatments that can reduce the infection within the host. Notably, increasing the death rate of infected cells leads to a decrease in the number of free virus particles, as depicted in Fig. 6. To further examine the influence of \(d_3\), the most sensitive parameter, we plot the variation of \(R_0\) with different values of other parameters in Fig. 7. This analysis provides valuable insights into the interplay between key parameters and their impact on the spread of the infection within the host.
The basic reproductive number \(R_0\) with respect to \(d_3\) for different values of other parameters. Identifying \(d_3\) as the most sensitive parameter highlights its significant influence on the within-host dynamics. This knowledge aids in prioritizing interventions targeting infected cells, potentially leading to improved patient outcomes by modulating \(d_3\).
Another control measure is the elasticity index which measures the change of \(R_0\) with respect to the change in the parameters. The elasticity of \(R_0\) with respect to the parameter \(\omega \) can be calculated by \(\Upsilon _{R_0}^\omega = \dfrac{\partial R_0}{\partial \omega } \times \dfrac{\omega }{R_0}\). Consequently,
The elasticity of \(R_0\) exhibits positive correlations with respect to the parameters \(\beta , p\) and k. Decreasing these parameters leads to a reduction in the value of \(R_0\), indicating that the infection can be effectively eliminated from the human body. Conversely, negative correlations are observed with parameters \(d_2\) and \(d_3\). This implies that increasing the death rates of latent cells and infected cells, possibly through treatments such as plasma therapy, monoclonal antibodies, and immune system-boosting foods, can contribute to the eradication of the disease. These correlation relationships, highlighting the impact of parameter changes on \(R_0\), are visualized in Fig. 8. Understanding these relationships is crucial for designing effective interventions and treatment strategies to combat the infection.
There is a positive correlation between \(R_0\) and T(0) which means a larger initial number of target cells T(0) in a limited cell population can lead to a higher probability of infection and potentially faster virus spread.
Based on this discussion, there are additional real applications to the considered problem. Firstly, in Treatment Optimization, the sensitivity analysis identifying the death rate of infected cells as a critical parameter can inform the development of enhanced treatment strategies, leading to improved patient outcomes. Secondly, in Vaccine Development, the incorporation of latent class analysis into our model enables its use in assessing and refining COVID-19 vaccine candidates, aiding in the development and evaluation of effective vaccination strategies. Lastly, in Risk Assessment and Management, our model’s sensitivity analysis offers valuable insights into the relative significance of various parameters in shaping disease outcomes. This information can assist in conducting risk assessments, informing mitigation strategies, and efficiently allocating healthcare resources.
Conclusion and further directions
In this study, we present a novel formulation of a within-host COVID-19 mathematical model. Unlike previous studies, our model takes into account the latent class, providing a new perspective on disease dynamics. We examine the nonnegativity and ultimate boundedness of the analytical solution to gain insights into the behavior of the system. Furthermore, we investigate the extinction and persistence of the disease within the human body by analyzing the local and global stability of equilibrium states, specifically \(E_0\) and \(E^*\). To support our findings, we perform numerical simulations and validate the results through the examination of sensitivity and elasticity of \(R_0\) concerning the model’s parameters. Our results reveal that the disease dies out when \(R_0 < 1\) without treatment, whereas it persists when \(R_0 > 1\). Of notable importance is the death rate of infected cells, which emerges as a highly sensitive parameter that can be enhanced through appropriate medical therapy and a diet that supports the immune system. Additionally, we propose that our research can be expanded to incorporate discrete and distributed delays, further enhancing our understanding of the disease dynamics. Moreover, fractional models offer a more accurate representation of complex and heterogeneous systems. They capture the intricate nature of disease transmission, taking into account factors such as varying susceptibility, heterogeneous mixing patterns, and non-integer order derivatives42,43.
Data availability
All data used in this manuscript have been presented within the article.
Code availability
The codes used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Zhu, H., Wei, L. & Niu, P. The novel coronavirus outbreak in Wuhan, China. Glob. Health Res. Policy 5, 1–3 (2020).
Lau, H. et al. The positive impact of lockdown in Wuhan on containing the covid-19 outbreak in china. J. Trav. Med. 27(3), 1–10 (2020).
El-Metwally, H., Sohaly, M. A. & Elbaz, I. M. Stochastic global exponential stability of disease-free equilibrium of hiv/aids model. Eur. Phys. J. Plus 135(10), 1–14 (2020).
Rangayasami, A. et al. Influence of nanotechnology to combat against covid-19 for global health emergency: A review. Sens. Int. 2, 100079 (2021).
Sanyaolu, A. et al. Comorbidity and its impact on patients with covid-19. SN Compr. Clin. Med. 2, 1069–1076 (2020).
Singhal, T. A review of coronavirus disease-2019 (covid-19). Indian J. Pediatr. 87(4), 281–286 (2020).
Li, Z. et al. Active case finding with case management: The key to tackling the covid-19 pandemic. The Lancet 396(10243), 63–70 (2020).
El-Metwally, H., Sohaly, M. A. & Elbaz, I. M. Mean-square stability of the zero equilibrium of the nonlinear delay differential equation: Nicholson’s blowflies application. Nonlinear Dyn. 105(2), 1713–1722 (2021).
Almutairi, A., El-Metwally, H., Sohaly, M. A. & Elbaz, I. M. Lyapunov stability analysis for nonlinear delay systems under random effects and stochastic perturbations with applications in finance and ecology. Adv. Diff. Equ. 2021(1), 1–32 (2021).
Coburn, B. J., Wagner, B. G. & Blower, S. Modeling influenza epidemics and pandemics: Insights into the future of swine flu (h1n1). BMC Med. 7(1), 1–8 (2009).
Casagrandi, R., Bolzoni, L., Levin, S. A. & Andreasen, V. The sirc model and influenza A. Math. Biosci. 200(2), 152–169 (2006).
Elbaz, I. M., Sohaly, M. A. & El-Metwally, H. Stochastic hiv/aids dynamics with discrete and distributed delays. Pramana 96(1), 1–15 (2022).
Pang, J., Cui, J. & Hui, J. The importance of immune responses in a model of hepatitis B virus. Nonlinear Dyn. 67(1), 723–734 (2012).
Yong, B. & Owen, L. Dynamical transmission model of mers-cov in two areas. AIP Conf. Proc. 1716, 020010 (2016).
Elbaz, I. M., Sohaly, M. A. & El-Metwally, H. Modeling the stochastic within-host dynamics sars-cov-2 infection with discrete delay. Theor. Biosci. 141(4), 365–374 (2022).
Prem, K. et al. The effect of control strategies to reduce social mixing on outcomes of the covid-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 5(5), e261–e270 (2020).
Peyraud, R. et al. Advances on plant–pathogen interactions from molecular toward systems biology perspectives. Plant J. 90(4), 720–737 (2017).
Gallagher, M. E., Brooke, C. B., Ke, R. & Koelle, K. Causes and consequences of spatial within-host viral spread. Viruses 10(11), 627 (2018).
London School of Hygiene Vaccine Centre and Tropical Medicine. Covid-19 vaccine development pipeline (refresh url to update). (2021).
So, A. D. & Woo, J. Reserving coronavirus disease 2019 vaccines for global access: Cross sectional analysis. BMJ 371, 1–10 (2020).
Rahimi, I., Chen, F. & Gandomi, A. H. A review on covid-19 forecasting models. Neural Comput. Appl. 1, 1–11 (2021).
Nabi, K. N. Forecasting covid-19 pandemic: A data-driven analysis. Chaos Solitons Fract. 139, 110046 (2020).
Ioannidis, J. P. A., Cripps, S. & Tanner, M. A. Forecasting for covid-19 has failed. Int. J. Forecasting 1, 1–10 (2020).
Guan, W. et al. Clinical characteristics of coronavirus disease 2019 in China. N. Engl. J. Med. 382(18), 1708–1720 (2020).
Long, Q.-X. et al. Antibody responses to sars-cov-2 in patients with covid-19. Nat. Med. 26(6), 845–848 (2020).
Robbiani, D. F. et al. Convergent antibody responses to sars-cov-2 in convalescent individuals. Nature 584(7821), 437–442 (2020).
Hamming, I. et al. Tissue distribution of ace2 protein, the functional receptor for sars coronavirus: A first step in understanding sars pathogenesis. J. Pathol. 203(2), 631–637 (2004).
Zhao, Y. et al. Single-cell rna expression profiling of ace2, the putative receptor of Wuhan 2019-ncov. Biorxiv 2020, 1–10 (2020).
Li, C., Xu, J., Liu, J. & Zhou, Y. The within-host viral kinetics of sars-cov-2. BioRxiv 1, 1–10 (2020).
Nath, B. J., Dehingia, K., Mishra, V. N., Chu, Y. & Sarmah, H. K. Mathematical analysis of a within-host model of sars-cov-2. Adv. Diff. Equ. 2021(1), 1–11 (2021).
Iqbal, Z. et al. Structure preserving algorithm for fractional order mathematical model of covid-19. Comput. Mater. Contin. 1, 2141–2157 (2022).
Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Mod. 2(3), 288–303 (2017).
DeJesus, E. X. & Kaufman, C. Routh–Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 35(12), 5288 (1987).
La Salle, J. P. The Stability of Dynamical Systems (SIAM, 1976).
Islam, M. A. et al. A comparative study on numerical solutions of initial value problems (ivp) for ordinary differential equations (ode) with euler and runge kutta methods. Am. J. Comput. Math. 5(03), 393 (2015).
Ali, J. et al. Evolutionary optimized padé approximation scheme for analysis of covid-19 model with crowding effect. Oper. Res. Perspect. 8, 100207 (2021).
Ahmed, N., Elsonbaty, A., Raza, A., Rafiq, M. & Adel, W. Numerical simulation and stability analysis of a novel reaction-diffusion covid-19 model. Nonlinear Dyn. 106, 1293–1310 (2021).
Farooqi, A. et al. A comparative epidemiological stability analysis of predictor corrector type non-standard finite difference scheme for the transmissibility of measles. Results Phys. 21, 103756 (2021).
Heffernan, J. M., Smith, R. J. & Wahl, L. M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2(4), 281–293 (2005).
Omame, A. & Abbas, M. Modeling sars-cov-2 and hbv co-dynamics with optimal control. Physica A 615, 128607 (2023).
Omame, A., Isah, M. E. & Abbas, M. An optimal control model for covid-19, zika, dengue, and chikungunya co-dynamics with reinfection. Opt. Control Appl. Methods 44(1), 170–204 (2023).
Ahmad, R. et al. A new fractional-order stability analysis of sir model for the transmission of buruli disease: A biomedical application. Fractals 30(05), 1–11 (2022).
Omame, A., Okuonghae, D., Nwajeri, U. K. & Onyenegecha, C. P. A fractional-order multi-vaccination model for covid-19 with non-singular kernel. Alexandria Eng. J. 61(8), 6089–6104 (2022).
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Contributions
The study presented here was carried out in collaboration between both authors I.M.E. and M.A.S. contributed to the selection and interpretation of the model. The theoretical analysis, numerical simulation of the model, and drafting of the manuscript were carried out by I.M.E. Critical revision of the manuscript was contributed to by H.M.E. and I.M.E.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elbaz, I.M., El-Metwally, H. & Sohaly, M.A. Viral kinetics, stability and sensitivity analysis of the within-host COVID-19 model. Sci Rep 13, 11675 (2023). https://doi.org/10.1038/s41598-023-38705-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-023-38705-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.