Introduction

The magneto-caloric effect (MCE) is a well-known interesting phenomenon that involves a change in the temperature upon applying/removing an external magnetic field. Its physics and applications are of continuous interest to researchers worldwide. [e.g.,1,2].

Some of the intermetallic compounds that exist in the rare-earth-iron system are, for example, RFe2, RFe3, R6Fe23 and R2Fe173,4,5. Much work has been dedicated to the magnetic properties of those compounds. The RT2 compounds, where T = Fe, Co, have been also investigated6,7,8,9. Roe et al.10 determined the magnetic structure of the iron-holmium binary system. Hoffer and Salmans11 measured the magnetization of the RFe3 compounds as function of temperature. On the application side, magnetic refrigerators, in particular those operating close to room temperature are a subject of extensive research. One of the reasons of such interest in the magnetocaloric-based refrigerators are the relatively higher efficiency and the lower impact on environment as compared to the conventional ones12,13. Rare-earth intermetallic compounds were a subject of many works due to their distinguished electronic, magnetic and magnetocaloric properties14,15,16,17,18. The RFe3 compounds, in particular, are of interest for both their magnetostrictive and magnetic properties19,20,21, however not much investigations were done on their magnetocaloric properties.

Our motivation, in this paper, is studying the magnetothermal and the magnetocaloric effect in YFe3 and HoFe3, using both ab initio calculation and the molecular field theory, in the two-sublattice model22,23,24. We report on both temperature and magnetic field dependences of magnetization, magnetic specific heat magnetic entropy, isothermal change in entropy and adiabatic change in temperature in the temperature interval of 0–800 K. We report on new calculation of the elastic constants, the bulk, the shear moduli and the electronic and lattice contributions to the total heat capacity and entropy using the well-known WIEN2k code package25,26,27,28,29. Another motivation of the present work is studying the order of the phase transition in these compounds in the light of the dependence of their properties on both temperature and field.

To calculate the elastic moduli of YFe3 we used the linear augmented plane-wave (LAPW) method by WIEN2K code30. This Package uses the energy approach calculation 31 that calculates the elastic constants by second-order derivative. The results of these calculations are then used to calculate the Debye temperature and the electronic heat capacity coefficient for \({\text{ YFe}}_{3}\). These two parameters for HoFe3 are obtained from available published data (Persson, the materials project)32.

Computational methods

DFT

The Wien2K electronic structure code is based on the Density Functional Theory (DFT)33. It employs the Full-Potential Linearized Augmented Plane Wave (FPLAPW)34. For correlation and exchange potentials, the Wien2k code30 employs the Local Density Approximation (LDA) of Perdew and Wang35 and the Generalized Gradient Approximation (GGA) of Perdew, Burke, and Ernzerhof36. Core and valence states are calculated in a self-consistent manner. For the spherical part of the potential, the core states are treated fully relativistically, while the valence states are treated using the full potential. To reduce linearization errors in R and Fe spheres, local orbital extensions37 with a converged basis of approximately 1000 basis functions are used. For the self-consistent band structure calculations, we used the modified tetrahedron method for Brillouin zone integration. Self-consistent calculations were performed, and convergence was checked by varying the number of k points in the irreducible Brillouin zone up to 64 points The ab initio calculated elastic properties of different systems have been reported, e.g. for YFe538, PrX2 (X = Fe, Mn, Co) compounds39, Cr-based full-Heusler alloys40 and GdFe241. Also ab initio calculation on the effect of applying pressure on PtXSb and GdN systems were reported, respectively by Habbak et al.42 and Reham Shabara et al.43. Magnetic properties and electronic structure of ThCo4B were reported by Abu-Elmagd et al.44 and Sherif Yehia et al.45 have reported on the spin and charge density maps of SmCo5.

Elastic properties

The Lagrangian theory of elasticity is used to describe the elastic properties. According to this theory, a solid is a homogeneous and anisotropic elastic medium. As a result, strains (defined as the fractional change in length) are homogeneous and can be represented using symmetric second rank tensors.

$$\partial_{ij} = \varepsilon_{ij} + \frac{1}{2}\mathop \sum \limits_{k} \varepsilon_{ik} \varepsilon_{kj}$$
(1)

where ∂ is the Lagrangian strain and εij are homogeneous strain parameters and i and j indicate Cartesian components44.

When we cast a crystal structure's Bravais lattice vectors, under an isotropic pressure, in a matrix form (R), the small homogeneous deformation (strain) distorts the Bravais lattice vectors of this crystal and hence cause a distortion of the lattice (R’) expressed by multiplying with a symmetric deformation matrix i.e. (R’ = R*D), where D is:

$$D = I + \varepsilon = \left( {\begin{array}{*{20}c} {1 + \varepsilon_{11} } & {\varepsilon_{12} } & {\varepsilon_{13} } \\ {\varepsilon_{21} } & {1 + \varepsilon_{22} } & {\varepsilon_{23} } \\ {\varepsilon_{31} } & {\varepsilon_{32} } & {1 + \varepsilon_{33} } \\ \end{array} } \right)$$
(2)

where I is a unique matrix that represents the symmetric strain tensor.

Now, we express the total energy of a crystal (R’), under strain in terms of a power series of the Lagrangian strain (∂):

$$E\left( {\partial ,V} \right) = E_{0} + V_{0} \mathop \sum \limits_{ij} \left( {\tau_{ij} \partial_{ij} } \right) + \frac{{V_{0} }}{2}\mathop \sum \limits_{ijkl} \left( {C_{ijkl} \partial_{ij} \partial_{kl} } \right)$$
(3)

where E (E0) is the energy and V (V0) is the volume of strained system.

The current \({\text{RFe}}_{3}\) compounds (R = rare earth) crystallize in the \({\text{PuNi}}_{3}\)-type structure, with space group 194-P63/mmc (Hexagonal).

C11, C12, C13, C33, and C55 are the five independent elastic constants for a hexagonal symmetry. We need five different strains to determine these elastic constants because we have five independent elastic constants. The five distortions are discussed further below. The first distortion46 is as follows:

$$\left( {\begin{array}{*{20}c} {1 + \delta } & 0 & 0 \\ 0 & {1 + \delta } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right)$$
(4)

and it modifies the basal plane while keeping the z-axis constant. As a result, the symmetry of the strained lattice remains hexagonal, and the energy for this distortion can be calculated as follows:

$$E\left( {V,\delta } \right) = E\left( {V_{0} ,0} \right) + V_{0} \delta \left( {\tau_{1} + \tau_{2} } \right) + V_{0} \left[ {\left( {C_{11} + C_{12} } \right)\delta^{2} + O\left( {\delta^{3} } \right)} \right]$$
(5)

The second type of distortion is a volume-conserved distortion and lead to orthorhombic symmetry and written as:

$$\left( {\begin{array}{*{20}c} {\left( {\frac{1 + \delta }{{1 - \delta }}} \right)^{1/2} } & 0 & 0 \\ 0 & {\left( {\frac{1 - \delta }{{1 + \delta }}} \right)^{{^{1/2} }} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right)$$
(6)

and the energy for this distortion can be obtained as:

$$E\left( {V,\delta } \right) = E\left( {V_{0} ,0} \right) + V_{0} \left[ {\left( {C_{11} + C_{12} } \right)\delta^{2} + O\left( {\delta^{3} } \right)} \right]$$
(7)

The third strain we have used is given by:

$$\left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & {1 + \delta } \\ \end{array} } \right)$$
(8)

This strain changes C lattice parameter and keeps the strained lattice's symmetry hexagonal, and the energy for this distortion can be obtained by

$$E\left( {V,\delta } \right) = E\left( {V_{0} ,0} \right) + V_{0} \delta \left( {\tau_{3} } \right) + V_{0} \left[ {\left( {C_{33} } \right)\frac{{\delta^{2} }}{2} + O\left( {\delta^{3} } \right)} \right]$$
(9)

The fourth elastic constant, C55, is determined by a lattice deformation that results in a low-symmetry object. The deformation is written as follows:

$$\left( {\begin{array}{*{20}c} 1 & 0 & \delta \\ 0 & 1 & 0 \\ \delta & 0 & 1 \\ \end{array} } \right)$$
(10)

and it leads to triclinic symmetry and the energy for this deformation can be written as:

$$E\left( {V,\delta } \right) = E\left( {V_{0} ,0} \right) + V_{0} \delta \left( {\tau_{5} } \right) + V_{0} \left[ {\left( {2C_{55} } \right)\delta^{2} + O\left( {\delta^{3} } \right)} \right]$$
(11)

Finally, the last strain we have used is volume-conserved, keeps the symmetry of the strained lattice hexagonal, and can be written as:

$$\left( {\begin{array}{*{20}c} {\left( {1 + \delta } \right)^{ - 1/3} } & 0 & 0 \\ 0 & {\left( {1 + \delta } \right)^{ - 1/3} } & 0 \\ 0 & 0 & {\left( {1 + \delta } \right)^{2/3} } \\ \end{array} } \right)$$
(12)

and the energy for this strain is given by

$$E\left( {V,\delta } \right) = E\left( {V_{0} ,0} \right) + V_{0} \left[ {\left( {C_{zz} } \right)\frac{{\delta^{2} }}{9} + O\left( {\delta^{3} } \right)} \right]$$
(13)

and

$$C_{ZZ} = C_{11} + C_{12} + 2C_{33} - 4C_{13}$$
(14)

Isotropic elastic constants such as the bulk, shear, and Young moduli can be determined using appropriate averaging procedures. All the previous parameters including the Young modulus, E, and the Poisson ratio, ν, the bulk modulus, B, and the shear modulus, G are calculated by IRelast Package47 as available in the Wien2k Package48. As for the crystal structure of the two compounds: YFe3 crystallizes in the hexagonal structure with space group P63/mmc and HoFe3 crystallizes in the trigonal structure with \({\overline{\text{R}}\text{3m}}\) space group. All the information about the lattice parameters and the locations of the Y or Ho and Fe atoms in the unit cells is available32.

Thermomagnetic properties

The total effective fields of the R and Fe sublattices are expressed as follows by molecular field theory (MFT):

$${\overline{\text{H}}}_{{\text{R}}} \left( {\text{T}} \right) = {\overline{\text{H}}} + {\text{d}}\left[ {{\text{n}}_{{{\text{RR}}}} \overline{\mu }_{{\text{R}}} \left( {\text{T}} \right) + 3{\text{n}}_{{{\text{RF}}}} \overline{\mu }_{{\text{F}}} \left( {\text{T}} \right)} \right]$$
(15)
$${\overline{\text{H}}}_{{\text{F}}} \left( {\text{T}} \right) = {\overline{\text{H}}} + {\text{d}}\left[ {3 {\text{n}}_{{{\text{FF}}}} \overline{\mu }_{{\text{F}}} \left( {\text{T}} \right) + {\text{n}}_{{{\text{RF}}}} \overline{\mu }_{{\text{R}}} \left( {\text{T}} \right)} \right]$$
(16)

In these equations \({\overline{\text{H}}}\) represents the applied field, \(\overline{\mu }_{{\text{F}}}\) the magnetic moment per Fe ion at temperature T in units of the Bohr magneton (\(\mu_{{\text{B}}}\)), and \(\overline{\mu }_{{\text{R}}}\) the magnetic moment per rare-earth ion. The factor d converts the moment per \({\text{RFe}}_{3}\) unit from \(\mu_{{\text{B}}}\) to gauss:

$${\text{d}} \equiv \frac{{{\text{N}}_{{\text{A}}} \mu_{{\text{B}}} {\uprho }}}{{\text{A}}}$$
(17)

where NA is Avogadro's number, ρ the density in \({\text{g}}/{\text{cm}}^{3}\), and A is the \({\text{RFe}}_{3}\) formula weight in g/mol. With these definitions the fields: \({\overline{\text{H}}}\),\({\overline{\text{H}}}_{{\text{R}}}\) and \({\overline{\text{H}}}_{{\text{F}}}\) are specified in gauss, and the molecular field coefficients \({\text{n}}_{{{\text{RR}}}}\),\({\text{n}}_{{{\text{RF}}}}\) and \({\text{n}}_{{{\text{FF}}}}\) respectively, describing the R-R, R-Fe, and Fe–Fe magnetic interactions, are dimensionless.

We begin with the magnetic energy of a binary magnetic compound to calculate the magnetic specific heat.

$$U = - \frac{1}{2}\left[ {n_{RR} M_{R}^{2} \left( T \right) + 9 n_{FF} M_{F}^{2} \left( T \right) + 6n_{RF} M_{R} \left( T \right)M_{F} \left( T \right)} \right]$$
(18)

The magnetic specific heat is calculated as follows:

$${\text{C}}_{{\text{m}}} \left( {{\text{T}},{\text{H}}} \right) = \left( {\frac{{\partial {\text{U}}\left( {{\text{T}},{\text{H}}} \right)}}{{\partial {\text{T}}}}} \right)_{H}$$
(19)

The magnetic entropy is calculated from the numerical integration of the magnetic heat capacity as follows:

$${\text{S}}_{{\text{m}}} \left( {{\text{T}},{\text{H}}} \right) = \mathop \int \limits_{0}^{{\text{T}}} \frac{{{\text{C}}_{{\text{m}}} \left( {{\text{T}},{\text{H}}} \right)}}{{\text{T}}}{\text{dT}}$$
(20)

The total heat capacity \({\text{C}}_{{{\text{total}}}}\) is made up of three contributions: the lattice heat capacity \({\text{ C}}_{{\text{l}}}\), the electronic heat capacity \({\text{C}}_{{\text{e}}}\) and the magnetic heat capacity \({\text{ C}}_{{\text{m}}}\):

$${\text{C}}_{{{\text{total}}}} = {\text{C}}_{{\text{l}}} + {\text{C}}_{{\text{e}}} + {\text{C}}_{{\text{m}}}$$
(21)

The lattice heat capacity is expressed as:

$${\text{C}}_{{\text{l}}} = 9{\text{R}}\left[ {4\left( {\frac{{\text{T}}}{{\theta_{{\text{D}}} }}} \right)^{3} \mathop \int \limits_{0}^{{\text{x}}} \frac{{{\text{x}}^{3} }}{{{\text{e}}^{{\text{x}}} - 1}}{\text{dx}} - \frac{{\text{x}}}{{{\text{e}}^{{\text{x}}} - 1}}} \right]$$
(22)

where \({\text{x}} = \theta_{{\text{D}}} /{\text{T}}\) and \(\theta_{{\text{D}}}\) is Debye temperature, which can be calculated using Eq. (23)49

$$\theta_{{\text{D}}} = \frac{{\text{h}}}{{{\text{k}}_{{\text{B}}} }}\left[ {\frac{{3{\text{n}}}}{{4{\uppi }}}\left( {\frac{{{\text{N}}_{{\text{A}}} }}{{\text{A}}}\rho } \right)} \right]^{1/3} {\text{v}}_{{\text{m}}}$$
(23)

where h is the Planck's constant, \({\text{k}}_{{\text{B}}}\) is the Boltzmann constant,\({\text{v}}_{{\text{m}}}\) is the average sound velocity, and n is the number of atoms per formula unit50. Equation (24) gives the average sound velocity in a polycrystalline material:

$${\text{v}}_{{\text{m}}} = \left[ {\frac{1}{3} \left( {\frac{2}{{{\text{v}}_{{\text{l}}}^{3} }} + \frac{1}{{{\text{v}}_{{\text{s}}}^{3} }}} \right)} \right]^{{ - \frac{1}{3}}}$$
(24)

where \({\text{v}}_{{\text{l}}}\) and \({\text{v}}_{{\text{s}}}\) are, respectively, the longitudinal and transverse sound velocities, which can be calculated using the shear and the bulk moduli G and B, from Navier’s equation51:

$${\text{v}}_{{\text{l}}} = \sqrt {\frac{{B + \frac{4G}{3}}}{\rho }} ,\;{\text{ and}}\; {\text{v}}_{{\text{s}}} = \sqrt {\frac{G}{\rho }}$$
(25)

The electronic heat capacity is given by:

$${\text{C}}_{{\text{e}}} = \frac{{\pi^{2} {\text{k}}_{{\text{B}}}^{2} {\text{D}}\left( {{\text{E}}_{{\text{F}}} } \right)}}{3}{\text{T}} = \gamma_{{\text{e}}} {\text{T}}$$
(26)

where \(\gamma_{{\text{e}}} = \frac{{\pi^{2} {\text{k}}_{{\text{B}}}^{2} {\text{D}}\left( {{\text{E}}_{{\text{F}}} } \right)}}{3}\) represents the electronic heat-capacity coefficient, and \({\text{D}}\left( {{\text{E}}_{{\text{F}}} } \right)\) represents the electron density of states at the Fermi energy \({\text{E}}_{{\text{F}}}\).

A magnetic conducting material's total entropy includes three contributions: lattice (\({\text{S}}_{{\text{l}}}\)), electronic (\({\text{S}}_{{{\text{el}}}}\)) and magnetic entropy (\({\text{S}}_{{\text{m}}}\)). The total entropy can be calculated by numerically integrating the total heat capacity:

$$S\left( T \right) = \mathop \int \limits_{{T_{1} }}^{{T_{2} }} \frac{{C_{H} \left( T \right)}}{T} {\text{d}}T$$
(27)

The lattice entropy is given by:

$$S_{l} = 3R\left[ {4\left( {\frac{T}{{\theta_{D} }}} \right)^{3} \mathop \int \limits_{0}^{{\frac{{\theta_{D} }}{T}}} \frac{{x^{3} }}{{e^{x} - 1}} {\text{d}}x - \ln (1 - e^{{ - \frac{{\theta_{D} }}{T}}} )} \right]$$
(28)

The electronic entropy is given, like the electronic heat capacity, by Eq. (26).

Magnetocaloric effect

The MCE is inherent in all magnetic materials and is induced by the magnetic lattice coupling with the applied magnetic field. The MCE is distinguished by two parameters: the adiabatic temperature change ΔTad (T, ΔH) and the isothermal entropy change \(\Delta {\text{S}}_{{\text{m}}}\)(T, ΔH). In an isothermal process, the entropy change caused by a magnetic field variation from H1 to H2, in compounds undergoing a second order phase transition, is calculated using the following Maxwell relation52:

$$\left( {\frac{{\partial {\text{S}}\left( {{\text{T}},{\text{H}}} \right)}}{{\partial {\text{H}}}}} \right)_{{\text{T}}} = \left( {\frac{{\partial {\text{M}}\left( {{\text{H}},{\text{T}}} \right)}}{{\partial {\text{T}}}}} \right)_{{\text{H}}}$$
(29)
$$\Delta {\text{S}}_{{\text{m}}} \left( {{\text{T}},\Delta {\text{H}}} \right) = \mathop \int \limits_{{{\text{H}}_{1} }}^{{{\text{H}}_{2} }} \left( {\frac{{\partial {\text{M}}\left( {{\text{H}},{\text{T}}} \right)}}{{\partial {\text{T}}}}} \right)_{{\text{H}}} {\text{dH}}$$
(30)

The adiabatic temperature change \(\Delta {\text{T}}_{{{\text{ad}}}}\) is calculated from the following equation:

$$\Delta {\text{T}}_{{{\text{ad}}}} \left( {{\text{T}},\Delta {\text{H}}} \right) = - \mathop \int \limits_{{{\text{H}}_{1} }}^{{{\text{H}}_{2} }} \frac{{\text{T}}}{{{\text{C}}\left( {{\text{T}},{\text{H}}_{{\text{F}}} } \right)}}\left( {\frac{{\partial {\text{M}}\left( {{\text{H}},{\text{T}}} \right)}}{{\partial {\text{T}}}}} \right)_{{\text{H}}} {\text{dH}}$$
(31)

It is clear from Eq. (31) that the total heat capacity is applied field-dependent. However if \({\text{C}}\left( {{\text{T}},{\text{H}}_{{\text{F}}} } \right)\) has a weak field dependence, we can rewrite Eq. (31) as follows53:

$$\Delta {\text{T}}_{{{\text{ad}}}} \left( {{\text{T}},\Delta {\text{H}}} \right) \approx \frac{{ - {\text{T}}}}{{{\text{C}}\left( {{\text{T}},{\text{H}}_{{\text{F}}} } \right)}}\mathop \int \limits_{{{\text{H}}_{1} }}^{{{\text{H}}_{2} }} \left( {\frac{{\partial {\text{M}}\left( {{\text{H}},{\text{T}}} \right)}}{{\partial {\text{T}}}}} \right)_{{\text{H}}} {\text{dH}}$$
(32)

Results and discussion

Density of states

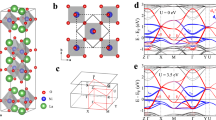
The Wien2K electronic structure code calculated the total DOS (density of states) for YFe3 and HoFe3 as shown in Figs. 1 and 2 respectively.

Figure 1
figure 1

The spin-up and spin-down electronic density of states (DOS) for YFe3.

Full size image
Figure 2
figure 2

The spin-up and spin-down electronic density of states (DOS) for HoFe3.

Full size image

The total DOS, at \({\text{E}}_{{\text{f}}}\) for these two compounds are 10.915 and 24.461 states/eV, respectively. Therefore the electronic heat capacity coefficients, as calculated from Eq. 26, are 0.0256 and 0.0575 J/mol. K2 respectively. The DOS of both compounds show that these two systems are metallic with fairly large density of states, at Fermi energy, in both the spin up and spin down configuration. This, of course, demands taking the electronic contribution to the heat capacity into consideration as we pointed out (Eq. 26).

Magnetization

Using the two-sublattice molecular field theory, the temperature dependence of magnetization of the rare earth and Fe sublattices, as well as total magnetization for \({\mathrm{YFe}}_{3}\) and \({\mathrm{HoFe}}_{3}\), are calculated. Total magnetic moments for \({\mathrm{YFe}}_{3}\) and \({\mathrm{HoFe}}_{3}\) ,calculated using the ab initio method are 4.8 µB/f.u and 4.4 µB /f.u, respectively, which are in good agreement with available experimental values, i.e. 4.88 and 4.59 µB /f.u as reported by J. F. Herbst et al.22. Table 1 displays the magnetic moments calculated in the present work and those by Ref.22. Figures 3 and 4a display mean-field- calculated temperature-dependence of magnetization, in zero field for \({\mathrm{YFe}}_{3}\) and \({\mathrm{HoFe}}_{3}\mathrm{respectively}\). The total magnetic moments of these two compounds, at very low temperatures, are in excellent agreement with the values referred to in Table 1. In addition we displayed, in Figs. 3 and 4b, both our mean field calculated magnetization and the experimental data extracted from Ref.22.

Table 1 Magnetic moments at very low temperature (~ 0 K) using our calculation, in comparison to experimental data.
Full size table
Figure 3
figure 3

Total magnetization of YFe3 in zero field vs. temperature.

Full size image
Figure 4
figure 4

(a) Mean-field calculated total and sublattice magnetization of HoFe3, in zero field, vs. temperature. (b) Total magnetization of HoFe3 vs. temperature.

Full size image

Ferromagnetic order for YFe3 is evident from Fig. 3 and the magnetic moment per Fe atom is about 1.6 µB in agreement with the value in Fig. 1 in Herbst work22. On the other hand, a ferrimagnetic order with a compensation point is found for HoFe3. As the magnetic moments of the Fe and Ho sublattices become equal and antiparallel, a cancellation of the total moment takes place close to 400 K. The continuous decrease in magnetization at Tc is a well-known feature of SOPT materials54.

The temperature dependence of the magnetization, in 1, 3, 5 and 7 T fields, for \({\mathrm{HoFe}}_{3}\), is shown in Fig. 5. an increase in the Curie temperature and a decrease in the compensation temperature is evident, with increasing the field. This behavior is consistent with that found in ferrimagnetic compounds, as reported for example, by P. von Ranke55. We may notice that even as the field increases the magnetization still has a continuous drop at Tc. Again, this confirms the SOPT nature of the studied compounds.

Figure 5
figure 5

Total magnetization of HoFe3 in different applied fields 1, 3, 5 and 7 T vs. temperature.

Full size image

Heat capacity and entropy

As previously stated, three contributions must be calculated to determine the total heat capacity of these materials. Figures 6 and 7 show, respectively, the magnetic heat capacity for \({\mathrm{YFe}}_{3}\) and \({\mathrm{HoFe}}_{3}\) in different applied fields. The features of these two figures, at the Curie temperature, show that the transition is a second order phase transition. In contrast, in the FOPT case, the peak in the heat capacity shifts to higher temperatures as the field increases53.

Figure 6
figure 6

Magnetic heat capacity of \({\mathrm{YFe}}_{3}\) , in different fields, vs. temperature.

Full size image
Figure 7
figure 7

Magnetic heat capacity of HoFe3 in different fields, vs. temperature.

Full size image

The calculated magnetic entropy, in fields in the range 0–6 T, is shown in Figs. 8 and 9 for YFe3 and HoFe3 respectively. The entropy saturates to its maximum at Tc and above, and is reduced by increasing the field. The maximum values of the calculated magnetic entropy are about 27.3 and 50.9 J/mol. K for YFe3 and HoFe3, respectively. These values are calculated using the equation:

$${\text{S}}_{{{\text{max}}}} = {\text{R }}\left[ {\ln \left( {2{\text{ J}}_{{\text{r}}} + 1} \right) + 3\ln \left( {2{\text{ J}}_{{{\text{Fe}}}} + 1} \right)} \right],$$
Figure 8
figure 8

The calculated magnetic entropy of \({\mathrm{YFe}}_{3}\) in two different fields vs. temperature.

Full size image
Figure 9
figure 9

The calculated magnetic entropy of \({\mathrm{HoFe}}_{3}\) in different fields vs. temperature.

Full size image

where Jr and JFe are the total angular momenta for the rare earth and Fe atoms, respectively. The molecular-field results of the maximum magnetic entropy is in very good agreement with the results of the equation shown above. The gradual increase of the magnetic entropy with temperature until it saturates at T ≥ Tc instead of the sudden increase found in FOPT materials show that the transition in these two compounds is a SOPT one.

Elastic properties of \(\mathbf{Y}{\mathbf{F}\mathbf{e}}_{3}\)

The elastic properties of YFe3 are calculated by using IRelast Package as available in the Wien2k Package47, the output of the program is shown in Table 2.

Table 2 The Elastic properties of YFe3 as obtained from IRelast Package.
Full size table

The Debye temperature is calculated from the mean sound velocity. The bulk and shear moduli of \({\mathrm{YFe}}_{3}\), using the Hill model, are 99.337 and 101.211 GPa, respectively. The calculated \({\theta }_{D}\) for \({\mathrm{YFe}}_{3}\) is 500.5 K. For the HoFe3 compound, the Debye temperature is 357.85 as reported by the Materials Project site (Kristin Persson)32.

Magnetocaloric effect

Isothermal entropy change

Figures 10 and 11 show the isothermal entropy change, for different magnetic fields, for \({\mathrm{YFe}}_{3}\) and \({\mathrm{HoFe}}_{3}\) respectively. The \(\Delta \mathrm{Sm}\) curve for \({\mathrm{HoFe}}_{3}\) exhibits two peaks: the first is a broad peak below the compensation temperature, and the second, smaller peak, has its maximum at the ferrimagnetic-paramagnetic phase transition at \({T}_{C}=590 K\). These two features correspond to the inverse and direct MCE effects, respectively. For ferromagnetic \({\mathrm{YFe}}_{3}\) there is only one peak at a temperature around its Tc (545 K). The temperature and field dependences of ∆Sm are those of SOPT materials. In particular, the curves at different fields have their maxima at Tc. In FOPT materials, the peak shifts to higher temperatures as the field increases53.

Figure 10
figure 10

Temperature dependence of isothermal change in entropy for YFe3 in fields: 2, 3, 4, 5 and 6 T.

Full size image
Figure 11
figure 11

Temperature dependence of isothermal change in entropy for HoFe3 in fields of 1, 2 and 3 T.

Full size image

Adiabatic change in temperature

We have calculated the adiabatic change in temperature for different field changes, as shown in Figs. 12 and 13, for YFe3 and HoFe3 systems, respectively. It is clear that the former compound has a higher cooling rate than the latter in agreement with reported literature56. For example, cooling rates about 1.3 and 0.4 K/T are achieved for these two compounds respectively for a field change of 3 T. The curves in each of Figs. 12 and 13 have their maxima centred at the Curie temperature. This is a known feature of compounds exhibiting second order phase transition and treated via the mean-field theory53.

Figure 12
figure 12

The field-dependence of the adiabatic change in temperature vs. temperature for \({\mathrm{YFe}}_{3}\).

Full size image
Figure 13
figure 13

The field-dependence of the adiabatic change in temperature vs. temperature for \({\mathrm{HoFe}}_{3}.\)

Full size image

The relative cooling power RCP (T)

The RCP is a figure-of-merit for MCE materials (e.g.56). It is defined as RCP (T) = ∆Tad (max) × δTFWHM. Table 3 displays the RCP (T) for benchmark materials e.g. Gd, Gd-based compounds and FeRh system. From this data, we may conclude that the RCP of YFe3 is comparable with those of well-known materials.

Table 3 The Relative Cooling Power RCP (T), using our calculation, in comparison to experimental data.
Full size table

The Arrott plots and universal curve

The Arrott plots for YFe3 are shown, in a temperature range around Tc, in Fig. 14. The positive slopes at those temperatures, below and above Tc, are indicative of second order phase transition. First order transitions exhibit negative or s-shaped slopes57,58. The straight line starting near the origin is calculated at a temperature close to Tc (Fig. 3). The features of the universal curve, described below, supports the presence of SOPT as well.

Figure 14
figure 14

The Arrott plots, at different temperatures, for YFe3.

Full size image

The universal curves59, for YFe3, are shown in Fig. 15 for field changes of 3, 4, 5 and 6 T. The curves are collapsed on each other especially at high temperatures i.e. θ > 0. The parameter θ is given by: θ = (T − Tc) / (Tr − Tc), where Tr is a reference temperature defined as the temperature at which the following condition holds: ∆SM (Tr) = 0.7 (∆SM)peak. The collapse of the ΔSM curves is also indicative of second order phase transition, which is different from the features encountered in first order phase transitions60.

Figure 15
figure 15

The universal curve for YFe3.

Full size image

It would be of interest to support our finding that the mean field theory is suitable for explaining the physical properties. Therefore, calculating some of the critical exponents61,62,63,64,65 would be beneficial. We have calculated the exponent n in the relation:

$$\Delta S_{m} \sim H^{n}$$

from the field dependence of ΔSm close to Tc. The relation between n, β and γ is:

n = 1 + (β−1)/(β + γ) [e.g. 65, which can be used to evaluate γ if β is calculated from the relation:

$$M\sim \left( { - t} \right)^{\beta } H = 0, T < T_{c}$$

or calculate β, if γ is calculated from:\(\chi_{T} \sim t^{ - \gamma } ,H = 0, T > T_{c}\), where t = (T−Tc)/T. We have calculated β for YFe3 from its M-T data, in zero field, by taking the logarithm of M ~ (−t)β and performing the calculation for temperatures lower than Tc. We have obtained β around 0.52 for this compound. Therefore, the percentage error between our result and the value 0.5 of the mean-field is around 4%. The factor γ turned out to be around 0.92 for YFe3. In addition, we have calculated the critical exponent δ from the relation: δ = 1 + γ/β66 and found that δ = 2.8, which is close to the MFT value of 3. From the above analysis, we conclude that mean-field theory has fairly produced the critical exponents for YFe3. We would also emphasize the fact that the mean-field theory has its own limitations near Tc.

We should mention that other models e.g. 3D-Heisnberg, 3D- Ising and Tri-critical mean field model [e.g.67] may be used to study the critical exponents, however a future experimental and/or theoretical work, dedicated to this task, may shed more light on the most proper model.

Conclusions

The two-sublattice molecular field model was used for calculating the thermomagnetic properties for \({\mathrm{YFe}}_{3}\) and \({\mathrm{HoFe}}_{3}\). The temperature dependence of magnetization shows that \({\mathrm{YFe}}_{3}\) is ferromagnetic with a Curie temperature close to 537 K, while \({\mathrm{HoFe}}_{3}\) is a ferrimagnetic compound with a compensation point around 389 K and a Curie temperature close to 565 K. The bulk and shear moduli are calculated using the WIEN2K ab-initio electronic code for YFe3 system. Those moduli were used to calculate its Debye temperature (500.53 K). The Debye temperature of HoFe3 is obtained from the Materials Project site. Using the calculated DOS, at Fermi energy, the electronic heat capacity coefficient \({\gamma }_{e}\) was found to be 0.0256 and 0.0575 J/\({K}^{2}\) mole, for \({\mathrm{YFe}}_{3}\) and \({\mathrm{HoFe}}_{3}\) respectively. The isothermal change in entropy ∆Sm, for a field change of 3 T, is about 0.8 and 0.12 J/mole. K for these systems, respectively. The Y-system exhibits a larger adiabatic drop in temperature (1.3 K/T), for a 3 T field change, than the Ho-system (0.4 K/T). The relative cooling power RCP(T) of YFe3 is comparable to well-known MCE materials The temperature and field dependences of the magnetization, magnetic heat capacity, entropy, the MCE quantities together with the Arrott plots and universal curve, are all indicative of SOPT.