Introduction

The concept of universality has been extremely successful in classifying and characterising equilibrium states of matter. For example, there are different types of order in a magnetic material separated by a second-order phase transition at which the relevant physical properties become independent of the microscopic details of the system. This constitutes universality and allows to characterise an extensive range of different phenomena in terms of just a few classes governed by the same critical properties. In view of the intensifying discussion on the dynamics of many-body systems it is a pressing question whether also far away from the thermal limit the character of dynamical evolution can become independent of the microscopic details. For a closed system this would imply that in approaching a critical configuration the evolution must become independent of the particular initial state the system has started from and critical slowing down in the actual time evolution is observed. As a consequence, different types of dynamical evolution could be distinguished by means of universality classes.

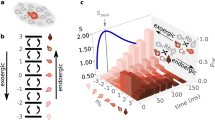
In this article, we demonstrate that such universal dynamics far from thermal equilibrium states is indeed possible. We show that there is a dynamical transition between different types of universal dynamics. After having quenched a two-component ultracold Bose gas we follow the ensuing evolution of the closed system and observe transient universal behaviour. In particular, we identify a tunable external parameter that determines the type of transient non-equilibrium order. In our setup non-equilibrium order is constituted by the appearance of spatial patterns including quasi-topological defects like vortices and skyrmions which are created through instabilities and which decay only on very large time scales1. We find the dynamics of diluting defects to constitute a separate dynamical critical phenomenon far from thermal equilibrium and therefore clearly distinct from the known equilibrium critical points2,3. Large-scale correlations in the system are universal in the sense that they are fixed by the type of defect, but are completely insensitive to the specific positions and velocities of the defects. Distinguishable types of defects are produced for different values of the tuning parameter. Hence, the dynamics can be tuned to a transition between different metastable non-equilibrium ordered states, see Figure 1. Extending upon the presented results will allow to learn about the universal properties of classes of models in the vicinity of attractors, non-thermal fixed points and other critical submanifolds of the greater space of all possible non-equilibrium configurations4,5,6,7. Knowing such universal properties, predictions for the behavior of very different physical systems can be obtained on the basis of comparatively few exemplary measurements. When looking at fundamental science applications, universality classes of far-from-equilibrium criticality can link the dynamics, which we propose to be observable in ultracold atomic or exciton-polariton gases, with phenomena as different as, e.g., magnon gases in solids, quark-gluon-plasma dynamics in heavy-ion collisions, or reheating after early-universe inflation. Technological applications would not stay away.

Figure 1
figure 1

Illustration of the dynamical evolution of a two-component Bose gas, with a focus on the possible transition between far-from-equilibrium transient states.

The set in the bottom left corner represents an ensemble of out-of-equilibrium initial states. Amongst these, a subset subjected to a dynamical instability is marked in white. It is chosen such that for all values of the the ratio α of inter- to intra-species couplings the system belongs to the unstable subset. Subsequently, the time evolution of the closed system leads to non- and quasi-topological defect formation. The type of defects created determines the scaling in the low-momentum regime of the particle spectrum of the gas. Our results reveal three different scalings corresponding to three types of defect configurations and a dynamical transition between the far-from-equilibrium universal states.

Full size image

The two-component Bose systems we consider are described by the Hamiltonian density ()

Here m is the mass of the atoms and α = g12/g the ratio between the inter-species coupling g12 and the intra-species interaction constant g. The latter as well as the mass are chosen to be the same for both components and the sum over the field index j ∈ {1, 2} is implied. The considered systems allow for good experimental control and have been studied intensely8,9,10,11. In experiment, α can be varied by means of a Feshbach resonance. Two different ground states exist, depending on the value of the parameter α12,13. In the immiscible regime, α > 1, the inter-species interaction energy is greater than the intra-species interactions. Hence, in the ground state, the spatial overlap of the components is minimised through domain formation and spatial separation of the two components. On the contrary, for α ≤ 1, the two components become miscible and, in the ground state, uniformly distributed over the whole volume. We make use of α to change the properties of the system in the yet unexplored region of non-equilibrium quasi-stationary states. A focus is set on long-lived states with non-/quasi-topological defects including domain walls8,12, single-species vortices and skyrmions14 in the coupled system.

Results

Since the dynamics we are interested in exclusively affects the low-momentum, strongly populated field modes, we employ the so-called classical field method which yields, within numerical accuracy, exact results for the time-evolving observables. In order to discuss the contribution of the different (quasi-)topological configurations in detail, we make use of the spin representation of the two-species fluid. In this representation the Sz-component of the spin vector simply refers to the density imbalance between the two species. This is an essential observable for the detection of domain walls. Furthermore, we make use of a hydrodynamic decomposition of the superfluid flow which allows for the detection of vortex contributions to the spectra. For details on numerical parameters and decomposition methods we refer the reader to the Methods section. In Figure 2, we unravel the time evolution of a two-component Bose gas as outlined in Figure 1. The parameters of our simulation are chosen such that the final states are close to the ground state of the system. To clarify the type of non-equilibrium order during the intermediate stages of the evolution, we show the imbalance between the two components Sz as well as the momentum distribution n(k) for three characteristic times. The initial time, tI, marks the stage of an isotropic momentum distribution which is overpopulated within an intermediate range of momenta, as compared to the ensuing equilibrium distribution. It is marked by a strong fall-off at large momenta. In our driving scheme this state is reached in the wake of an instability. For the immiscible case, α > 1, we use a modulational instability in which small low-momentum fluctuations in the polarisation are amplified to macroscopic spin domains. In the miscible regime, α ≤ 1, we invoke a counter-superflow instability15,16 by choosing oppositely directed flow vectors for the two field components. Above a critical relative velocity, momentum exchange between the two fluids causes the superflow to decay and spin domains to form. Subsequently, overpopulation at intermediate momenta is encountered for all values of the parameter α. Its microscopic origin is seen in the coloured distributions of the density imbalance Sz in Figure 2 which show strong fluctuations and the onset of domain formation. We estimate , with ωI being the energy of the fastest growing unstable mode. Note, that the dynamics up to tI is different for different α and involves for example isotropisation in case of α ≤ 0. For details see section A in the Supplementary Material. The further dynamical evolution of overpopulated states involves particle transport towards small momenta and energy transport towards high momenta17,18. In Figure 2 this is best observed by comparing the high momentum tails of the momentum distributions at tI and tNTFP. Particle transport towards low momenta eventually fills the zero-mode (not seen), a process most important in the miscible regime α = 0.8. The key insight gained from the spectra concerns the development of infrared (IR) power laws in the momentum distribution n(k) ~ k−ζ at . These power laws depend on the external parameter α: ζ ~ 3.5 for α > 1, ζ ~ 3 for α = 1 and ζ ~ 4 for α < 1. Also, the pattern of imbalance fluctuations in the system depends on the interaction strength.

Figure 2
figure 2

Time evolution of the system in three different parameter regimes.

Three snapshots (columns) of the evolving two-component Bose gas for three different values of the coupling ratio α (rows) are shown. In each case we show the spatial distribution of density imbalance Sz as well as the momentum distribution n(k) as a function of the momentum modulus k of particles in the gas. Tick labels for the spectra graphs are the same as in Figure 3. Until tI the dynamics is characterised by the instability and isotropisation of density fluctuations. At tNTFP = 10 tI, one observes the development of different power laws in the momentum distributions. They remain metastable for a long time beyond tF = 100 tI and reveal different non-thermal fixed points. The change of power laws at α = 1 indicates a dynamical transition.

Full size image

We highlight the most striking observations at late times before we carry on developing a detailed understanding of the relation between the dominant fluctuations and the observed power laws. In the immiscible regime the system consists of few large domains with additional inclusions of small point-like domains. As compared to the initial time domains have considerably grown. A special situation is encountered at the transition point (α = 1), where domain-like structures persist to extremely long times. This is remarkable since in this regime domains are not energetically favourable as compared to overlapping particle densities. For α = 0.8, imbalance fluctuations have decayed up to few small areas of strong imbalance. Let us finally look at the largest computed time . For α > 1, two domains of equal size remain, which reflects the immiscibility in the ground state. The small-scale domain-fluctuations have considerably reduced in number. At the transition point, we observe the persistence of domain-like structures which we attribute to a diverging time scale τ of domain decay as α → 1 from below. For details see section B in the Supplementary Material. For α < 1, small long-lived imbalance fluctuations remain, whereas the background tends to become very smooth, Sz ≈ 0. Finally, we investigate the microscopic origin of the scaling found in the momentum distributions. The bimodal power laws in these distributions are signatures of the system having approached a non-thermal fixed point4,5,6,7. At long times they become more pronounced in all three cases, signalling critical slowing down of the dynamic evolution. In Figure 3, the result of a decomposition of the momentum distribution according to spin and fluid degrees of freedom at t = tNTFP is presented, see the Methods section for details on the decomposition. We show spin-spin correlation functions as well as correlations in the incompressible velocity as a function of momentum. The crucial point is that they explain the scaling properties of the total momentum distribution and allow for an interpretation in terms of specific defect configurations, as shown in Figure 2. This completes our understanding of transient non-equilibrium order in a two-component ultracold Bose gas.

Figure 3
figure 3

Decomposition of correlation functions of the two-component Bose gas.

The three different graphs refer to the three different non-equilibrium ordered states parametrised by the coupling ratio α. Shown are the z-spin component , the sum of x- and y-spin components and the incompressible component ni at time tNTFP. For details of the decomposition procedure see the Methods section.

Full size image

We remark that, for all α, compressible and quantum pressure excitations, which are not shown, dominate the spectrum in the ultraviolet (UV) regime and follow a thermal Rayleigh-Jeans distribution n ~ k−2, while they give a negligible contribution towards lower momenta.

In the immiscible regime, see Figure 3 (left), the main contribution to the spectrum in the IR region is provided by the incompressible component ni, corresponding to flow orientations transverse to the direction in which the flow velocity varies. Although we are dealing with a multi-component gas this feature is similar to superfluid turbulent flow in a single-component Bose gas. Thereby the incompressible spectrum shows ni ~ k−4 scaling over approximately one decade which is generated by coherent vortical flows wi around topological defects17,18. The cores of these vortex-like structures can be seen in the spin imbalance, see Figure 2, since they are filled with particles of the other species and thus are of the skyrmion type. They are created during the merging process of domains and, persisting due to their topological nature, give the main contribution to the incompressible component spectrum. However, spin excitations overtake in an intermediate momentum region, showing a scaling of . Looking more closely, one observes that the scaling behaviour terminates in the IR at a scale π/LD given by the mean domain size LD, while the cut-off in the UV at π/ξs is set by the width of the domain walls, i.e., the spin healing length ξs = ξ(1/|1 − α|)1/2. Since the two contributions and ni are of comparable magnitude within an intermediate momentum range the sum of all contributions, giving the full spectrum n(k), appears to follow the power law n ~ k−3.5 in the IR, as discussed above.

The situation on the other side of the transition can also be clarified. When α falls below 1 domains are energetically suppressed. Thus, vortices dominate the non-thermal fixed point and induce the characteristic scaling n ~ ni ~ k−4, see Figure 3 (right). Here, it is also visible in the scaling of relative phase fluctuations , which is related to constant particle densities on scales larger than ξ as compared to the skyrmionic case above.

The picture changes dramatically on the transition point, α = 1. As shown in Figure 3 (middle), vortical flow is much less important in this regime. The momentum distribution is dominated by spin fluctuations scaling as . We attribute this feature to the increased dimensionality of the vacuum manifold for α = 1 which removes the topological protection of vortices. The stability of domain walls at the transition point takes over but is non-topological in nature. Instead, conservation laws restrict the decay of this particular type of defect19. This argument can be made even more transparent by studying the critical dynamics at the transition from α < 1 towards α = 1, where two non-equilibrium ordered states meet each other, vortices and domains. Details on the connection between defect structures and scaling exponents of the momentum distribution can be found in the Methods section.

Discussion

We conclude that the appearance of (non-)topological defects determining bulk features of correlation functions in far-from-equilibrium situations is very general and strongly relevant for intermediate-time universal dynamics. It is easily imaginable that multi-component field theories with more than two components show similar behavior to the one outlined here. We point out the possibility of a universal duality between diluting defects and inverse particle cascades. This requires the generation of (quasi-)topological configurations far from thermal equilibrium and their slow decay, going together with an increase of coherence and defect separation20. Under these conditions, an inverse particle cascade is generated and the associated power-laws can be found from the scaling properties of the respective single defect.

The cascades exhibit a characteristic non-thermal infrared power-law behaviour of correlation functions, e.g., as demonstrated in the paper, the momentum spectrum n(k) ~ k−ζ, . This scaling is distinctly different from the situation of a thermal gas and reflects a different relation between spectral and statistical correlations far from equilibrium. The scaling behaviour which is evolving further towards the infrared while the defects are being diluted marks the presence of a non-thermal fixed point. In the vicinity of this point, the time evolution becomes universal due to self-similarity in the scaling regime. We point out that universality, here, is not only related to the scaling in the spatial coordinates but is also present in the time dimension, manifesting itself e.g. in the cascading character of the scaling regime which is progressively building up coherent population in the infrared due to the dilution process of the topological defects. Furthermore, the time evolution of correlation functions can show scaling behaviour. We emphasise that adiabatic near-equilibrium descriptions of dynamical critical phenomena do not apply to the strong quench scenarios studied here, such that in principle new scaling exponents should appear which mark new universality classes of far-from-equilibrium critical dynamics, the determination of which is beyond the scope of this work.

We furthermore conclude that it is possible to establish the notion of a dynamical transition between different far-from-equilibrium ordered states in a two-component Bose gas. Tuning a system parameter (α) through a point where the symmetry properties of the system change allows the universal far-from-equilibrium dynamics, e.g., its scaling properties, change qualitatively. Hence, in what we call a dynamical transition, the way how non-thermal fixed points are approached during the equilibration evolution changes qualitatively. Determining how such a dynamical transition is related to a corresponding equilibrium transition, being beyond the scope of this work, poses an interesting question for the development of a theory of far-from-equilibrium critical phenomena.

A variety of (quasi-)topological excitations are known to exist in multi-component fields1,19, examples are monopoles in gauge fields21 and exotic magnets22, as well as skyrmions in Bose-Einstein condensates14,23 and liquid crystals24. New interesting features that are readily accessible in experiment are expected for ultracold spinor gases25,26,27,28,29. The transition between different types of transient non-equilibrium order can be controlled by changing the symmetry properties of the Hamiltonian and thus topology and local conservation laws of the system. This offers interesting prospects for far-from-equilibrium dynamical transitions in very different areas of physics.

Methods

Classical field equations

Since the dynamics we are interested in exclusively affects the low-momentum, strongly populated field modes, we employ the so-called classical field method which yields, within numerical accuracy, exact results for the time-evolving observables30,31. For this, initial field configurations φ1,2(x, t0) are sampled from Gaussian probability distributions and then propagated according to the classical equations of motion. At the end of the time evolution correlation functions are obtained from ensemble averages over the set of sampled paths. The classical equations of motion derived from the Hamiltonian density (1) of the interacting two-component Bose gas are

The momentum distribution which is shown in various graphs is defined as

where denotes the angular average in two-dimensional momentum space.

We have applied the following rescalings to obtain dimensionless quantities in the system of coupled Gross-Pitaevskii equations (2), using the lattice constant as of the computational grid: φas → φ, mg → g and . Here n = (N1 + N2)/L2 is the mean total particle density on a Ns × Ns grid of linear size L = Nsas, with Ns = 1024. Conversion to physical time scales appropriate for a specific experiment, with, e.g., 87Rb atoms, can be achieved by noting that the healing length ξ = (2mgn)−1/2 is given by ξ = 4as for our system. Giving an estimate, e.g., for a physical healing length , our lattice unit corresponds to which yields a time unit of . Hence, the characteristic time scale is which yields a realistic time scale for the appearance of the non-thermal fixed point at .

Spin-fluid representation

Although we always simulate the full set of equations (2) it is instructive to study the degrees of freedom which describe the relative evolution of the two components. Writing the fields in the polar representation these are given by the local phase difference θr = θ1 − θ2 and by the local density difference ρ1 − ρ2. The Pauli matrices σa serve to define the Schwinger representation (sum over repeated indices implied) of angular momentum operators. This results in a three-component vector of (pseudo-)spin densities Sa, a ∈ {x, y, z}

where the modulus corresponds to the total density |S| = ρ1 + ρ2 ≡ ρT. For convenience, we apply the redefinition Sa → ρTSa such that |S| ≡ 1. Then, the Hamiltonian density of Eq. (1) can be rewritten as

which shows the influence of the relative degrees of freedom and their coupling to the global ones32. The quantity jT = ρ1∇ϕ1 + ρ2∇ϕ2 is the conserved total particle current associated with a global U(1) symmetry of Eq. (1) associated with the global shift of the total phase θT = θ1 + θ2. Thus jT can not be expressed using just the spin densities but contains also the remaining fourth degree of freedom, the total phase θT. We obtain

According to the representation (5) of the Hamiltonian density the two-component Bose gas can be described by a spinor field S which is coupled to a hydrodynamic fluid with density ρT and (conserved) quasi particle current jT. For a fluid at rest, i.e., ρT = const and jT = 0, the spin system thereby assumes the form of a classical non-linear sigma model (NLσM) with a mass term , whereas in general a current jT ≠ 0 leads to a highly non-trivial coupling between internal and hydrodynamic degrees of freedom.

Hydrodynamic decomposition

In order to gain further insight into the interplay between the domain structure and other excitations we decompose the energy spectrum according to Refs. 18,33. The results of this decomposition at the non-thermal fixed point were discussed in Figure 3 of the main text. In a density-phase representation, the kinetic part of the Hamiltonian density can be written in the following way:

The velocity field w is defined via the total particle current , similar to the convenient choice for the one-component case. In this decomposition the first and the last terms are the quantum-pressure component and the classical hydrodynamic component, respectively. In contrast to a single-component fluid the second term of Eq. (7) adds a pressure-like contribution to the kinetic energy which is produced by internal excitations only. In addition, the velocity field w and thus the corresponding part of the kinetic energy can be decomposed in a compressible and an incompressible part, w = wc + wi, with ∇ × wc = 0 and ∇ · wi = 0, such that wave-like and vortical excitations appear in different parts of the decomposition, see Refs. 33. Based on Eq. (7), radial energy spectra in momentum space corresponding to the discussed energy parts can be defined as

Here we have introduced additional velocities and for the sake of a closed representation. Finally, the energy spectra can be converted to occupation number spectra defined in Eq. (3) by multiplication with a factor k−2, nδ(k) = k−2Eδ(k), δ ∈ {q, c, i, s}18.

Domain and vortex spectra

In Figure 3 of the main text we discussed the microscopic origin of characteristic power-laws in the momentum distribution n(k) by decomposing the spectra in different components. This was successful since signatures of different defects show up in specific components of the spectra. Here we make this correspondence explicit for the case of vortices and domain walls.

Under the assumption of spatially constant total particle density the spectrum ns can be related to the Fourier transform of the correlation function of the angle-averaged spin order parameter ,

with denoting the Fourier transform and therefore . Hence, in a momentum regime π/LD ≪ k ≪ π/ξs where the the scaling behaviour is dominated by a single domain wall, follows from an ansatz in terms of the Heaviside function Sz = ±(1 − 2θ(x)), Sx ≡ Sy ≡ 0. This feature is similar to the scaling induced by solitons in one-dimensional Bose gases, where the phase jump occurs in the bosonic field and induces a scaling n1D ~ k−2, see Ref. 34.

Similarly, the appearance of quantised vortices induces scaling behaviour of the incompressible energy ni. On scales considerably smaller than the mean distance between vortices, the effective velocity field |wi(r)| associated with the rotational flow decays as 1/r with growing distance r from the nearest vortex core. As a result, the angle-averaged incompressible kinetic energy distribution gives rise to the IR momentum spectrum ni(k) ~ k−4, whereas compressible excitations vanish.