Introduction

Electrowetting (EW)1, in which electric field is applied to modify the wetting properties2,3,4,5,6 of the substrate, is important for a variety of applications including micro/nano droplet manipulation7, E display8, lab on chip9, etc. While much progress has been made, most of the studies on EW were on rigid and fixed substrate. However, the wetting phenomena on soft and movable substrate, known as elasto-capillarity (EC)10, are more common both in engineering and biological systems, such as the stiction of micromachined cantilever beams in wet conditions11 or the closing hermetically of Nymphoides flowers when sink into water12. EC has been used to produce capillary origami of different shapes in experiments13 and Král group's pioneer work predicted that a nanodroplet could guide the graphene to fold by molecular dynamics (MD) simulations14. To realize the controllable and reversible process of EC, Zhao group has applied electric field in EC and named the combination of EW and EC the electro-elasto-capillarity (EEC)15,16. EEC deserves to be concerned of both science and applications. When placed on a soft substrate, a droplet, whose size is larger than the EC length17, can be spontaneously wrapped under the vertical component of surface tension and released by applying the electric field. The capillary force, elastic force and electric force compete in EEC. At the atomic scale, the precursor film (PF) produced by the droplet would interact with the soft substrate to unwrap the folding structure. EEC has been used to realize the revisable folding of capillary origami both in experiments16,18 and 2D MD simulations15. The controllable folding structure promises to be a good candidate in encapsulation and targeted releasing of drug, eliminating evaporation of small droplet16, improving the performance of photovoltaic systems19, etc. In this paper, we not only realized the EEC process by MD simulations, but also found the capillary wave propagation induced by the competition between two PFs during this process.

At nanoscale, the folding structure is pushed by the PF to unwrap during EEC as shown in Fig. 1b. PF, first proposed by Hardy20, is usually a molecular layer propagating ahead of the nominal contact line. When viewed at the atomic scale, the PF plays an important role in the dynamic wetting process on hydrophilic substrate. Besides, during EW, due to the long-ranged Coulomb interaction induced by the electric field, the ionized or polar deionized liquid molecules can also be attracted to the substrate to form the PF. The existence of the PF has been verified by numerous experiments21,22,23,24,25,26 and MD simulations15,27. Through theoretical analysis, de Gennes predicted that the PF was controlled by the disjoining pressure28. Previous studies were about single PF on rigid substrate. But there was no report on the coupled interaction between multilayer PFs to the best of our knowledge. In our work, during EEC, two PFs were formed as shown in Fig. 2c (the upper PF on the soft substrate and the lower PF on the rigid substrate). Through MD and theoretical analysis, we found that the two PFs competed to form the capillary wave at nanoscale. And this capillary wave was explored by molecular kinetic theory (MKT) in the atomic level for the first time.

Figure 1
figure 1

Molecular dynamics (MD) simulation domain of elasto-capillarity (EC) and electro-elasto-capillarity (EEC).

(a) The dynamic EC process of a water droplet wrapped by the graphene. (b) Schematic diagram of the unwrapping process of the folding structure pushed by the precursor film (PF) under the electric field. (c) MD simulation domain of EEC. Silver, red and ice blue atoms represent graphite, graphene and water atoms, respectively.

Full size image
Figure 2
figure 2

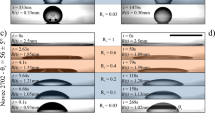
Capillary wave propagation (borderline between red and ice blue) induced by the competition between PF1 and PF2 during which the graphene was delaminated from the substrate by PF2.

(a–c) stage 1: wave propagating along the negative direction. (d–f) stage 2: wave propagating along the positive direction. (g–i) stage 3: formation of a stable wrinkle. (j–l) stage 4: disappearance of the wrinkle.

Full size image

In this paper, graphene was chosen as the soft substrate. A variety of applications has been spurred by graphene for its unique properties29,30,31,32. The key challenge for realizing these applications is the ability to produce and transfer graphene. Large area growth of graphene is on a substrate such as chemical vapor deposition on Pt33 or Cu34. However, due to the extremely large adhesion energy of graphene on the substrate35, delaminating and transferring graphene from the substrate is usually difficult. Graphene has been transferred by directly etching the substrate36. But, exposed to the etching solution, graphene is inevitably contaminated. In this paper, we found a candidate method for separating the graphene from the substrate without damage by the PF during the wave propagation.

We carried out MD simulations to realize the dynamic EEC process. Under the electric field, some water molecules were attracted to the graphene and others to the substrate to form the two PFs. The upper PF propagated to unwrap the folding graphene and the lower PF propagated to delaminate the graphene from the substrate, which was driven by the Maxwell stress as shown in Fig. 4b. During this process, we found the capillary wave propagation induced by the competition between the two PFs. The propagation of the capillary wave was explored by MKT. The theory and the simulations qualitatively agreed well on the velocity. From the perspective of wave dynamics, a scaling analysis was made to obtain the dispersion relation and the average wave velocity, which was of the same order with that in the simulations. From the theoretical analysis above, we concluded that the wave propagation was controlled by the driving work difference of the two PFs, while the energy was mainly dissipated by the viscosity. In addition, a series of EEC simulations under different electric field intensities (E) and different boundary conditions showed that the capillary wave velocity was insensitive to E and the boundary. It is expected that our work can provide valuable guidance for utilizing the PF to unwrap the folding structure or delaminate graphene from substrate.

Figure 4
figure 4

The atomic theory of the interaction between two PFs.

(a) Schematic diagram of the molecular kinetic theory (MKT). (b) The competition between two PFs.

Full size image

Results

First, a water droplet was placed on the graphene without electric field. Under the vertical component of surface tension, the droplet was spontaneously wrapped by the graphene in 0.08 ns (Fig. 1a) corresponding to the viscous time tvis ~ l/(γ /ηw) ~ 0.1 ns, where ηw = 0.001 Pa·s is the viscosity of bulk water, l = 8 nm the droplet diameter and γ = 0.072 N/m the surface tension. To release the droplet, an electric field was applied (Fig. 1b). During the releasing process, the elastic energy decreased, while the interface energy increased. Here, the folding graphene was pushed by the PF to unwrap when E ~ 1 V/nm. In the following results and discussions, E = 3 V/nm (Fig. 1c).

During EEC, PF spread on the soft graphene and the fixed graphite at the same time (Fig. 2). The upper PF on the graphene and the lower PF on the graphite were distinguished by PF1 and PF2, respectively (Fig. 2c). The competition between PF1 and PF2 induced the capillary wave propagation. The expanding wave velocity was defined to be negative (Fig. 2b) and the contracting wave velocity (Fig. 2e) to be positive. The whole EEC process was divided into four stages. In the first stage (Fig. 2a–c), the wave propagated along the negative direction and quickly accelerated in 0.015 ns. During this period, the folding graphene was unwrapped and pushed by PF1 with a force of the order of 10 nN/nm. Contemporarily, some water molecules were attracted to the graphite and formed PF2. When the disjoining pressure of PF2 was larger than that of PF1, the wave started slowing down and countermoved at 0.05 ns. In the second stage (Fig. 2d–f), PF2 drilled into the confined space between the graphene and the graphite driven by the Maxwell stress (see Supplementary Information 7), while PF1 started receding from the graphene. During this process, the capillary wave propagated along the positive direction and accelerated from 0.06 to 0.1 ns. Then the waves in the four flakes of the graphene encountered in the center and slowed down. In the third stage (Fig. 2g–i), a stable wrinkle formed in the graphene under the external pressure from PF2. The wrinkle remained for about 0.5 ns. It should be noted that the wrinkle was slowly shrinking, which was hard to be detected, while the curvature of the wrinkle simultaneously increased. In the fourth stage (Fig. 2j–l), the wrinkle quickly disappeared pressed by PF2. In the end, PF2 completely separated the graphene from the substrate (Fig. 2l). The wave propagation during EEC was also accompanied by the variation of the elastic strain energy of the graphene with respect to time.

The elastic strain energy of the graphene oscillated to decrease during EEC (Fig. 3). In the first stage, owing to the unwrapping of the folding graphene, the elastic strain energy decreased (shallow green line in Fig. 3). Then, pushed by PF2, the graphene was wrinkled, following which the four waves encountered in the center. This led to the increase of the elastic strain energy in the second stage (red line in Fig. 3). After a short relaxation, the elastic strain energy stabilized at 1.55×10−17 J, corresponding to the stable wrinkle of the third stage (deep green line in Fig. 3), which lasted for about 0.5 ns. In the fourth stage, the wrinkle disappeared, which resulted in the decrease of the elastic strain energy (blue line in Fig. 3). It should be noted that the elastic strain energy was mainly stored in the wrinkle, which was induced by the competition between PF1 and PF2, as shown in the inset of Fig. 3.

Figure 3
figure 3

The variation of the elastic strain energy of the graphene with respect to time.

The inset describes the distribution of the elastic strain energy of the graphene in which the energy gradually decreases from blue to red.

Full size image

Discussion

In the atomic level, we developed MKT proposed by Eyring et al37 to analyze the capillary wave propagation during EEC. In this theory, the motion of the contact line is determined by the adsorption and desorption of the fluid molecules on the surface sites separated by a distance λ0 (λ0 = 2.46 Å for graphene or graphite) as shown in Fig. 4a. For the surface sites with energy barrier of ΔGm, the equilibrium jump frequency of the fluid molecules κ0 = (kBT/h)exp(−ΔGm/kBT), where kB and h are the Boltzmann and Planck constant, respectively. The contact line would move if the adsorption equilibria are disturbed by the external driving work. In the case of EW, the driving work for the spreading droplet contains the van der Waals interactions per unit area wv, the polar interactions between water molecules wp, the different structure of the PF from the bulk liquid ws38 and additional average electric energy wE. So the total work that induces the motion of the contact line is w = wv+ wp+ ws+ wE15. For water droplet of nanoscale, the electric energy describing the interaction between the electric field and the droplet is , where is the electric field vector, the electric dipole moment and L(x) = coth(3x)−1/(3x) the Langevin function. All the forces that induced the driving work of the PF were contained into the disjoining pressure39, which could be obtained directly from MD results. In our simulations, the capillary wave propagation during EEC was induced by the competition between PF1 and PF2 (Fig. 4b). So the wave velocity can be calculated by

where w1 is the driving work per unit area of PF1, w2 that of PF2 and n the number of adsorption sites per unit area (n = 0.19 Å−2 for graphene or graphite). This is the governing equation of the competition between two PFs, in which w2−w1 and κ0 are variables.

Here, we discussed the wave in the left flake of the graphene (Fig. 4b). The wave propagating along the right direction was defined to be positive. As shown in Fig. 5a, w1 was monotonically decreasing in the first 0.05 ns; then stabilized at about 2.5 J/m2. Oppositely, w2 was monotonically increasing in the first 0.05 ns; then stabilized at about 3.5 J/m2. Before 0.05 ns, w2 < w1, which resulted in the wave propagating along the negative direction in the first stage (Fig. 2a–c). At 0.05 ns, w2 = w1, substituting which into equation (1), we obtained zero velocity. The wave countermoved at this moment. In the second stage, w2 > w1, the wave propagated along the positive direction (Fig. 2d–f). Then w2−w1 stabilized at about 1 J/m2 in the third stage (Fig. 2g−i). Considering the wrinkle area be about 1000 Å2, the stable work difference originating from w2−w1 was evaluated to be of the order of 10−17 J, which had the same order with the elastic strain energy stored in the stable wrinkle (deep green line in Fig. 3). From the analysis, we inferred that w2−w1 transferred to the elastic strain energy of the graphene wrinkle in the end.

Figure 5
figure 5

(a) Driving work per unit area of the two PFs from the MD simulations. (b) Driving work difference of the two competing PFs. The inset represents the competition between two PFs from the simulations. (c) Potential surface of the interaction between the PF and the substrate. The red colour represents high energy, whereas the blue colour represents low energy.

Full size image

To obtain the wave velocity from equation (1), the driving work difference w2−w1 and the equilibrium jump frequency κ0 should be obtained in advance. The driving work difference between PF2 and PF1, which drove the wave, was obtained from w2 and w1 illustrated above (Fig. 5a). As shown in Fig. 5b, w2−w1 was negative before 0.05 ns, which drove the wave propagating along the negative direction; then positive from 0.05 ns to 0.14 ns, which drove the wave propagating along the positive direction. After 0.14 ns, w2−w1 stabilized at about 1 J/m2, which transferred to the elastic strain energy stored in the stable wrinkle. We fitted w2−w1 by exponential function of the red line as shown in Fig. 5b.

Then, we endeavored to obtain the equilibrium jump frequency κ0. From Blake's theory40, the fluid molecules within the contact line are hindered not only by interactions with solid surface (adhesion), but also by viscous interactions with neighboring fluid molecules. So the energy barrier ΔGm = ΔGa+ΔGv, where ΔGa and ΔGv are the contributions from adhesion and viscosity, respectively. According to Eyring's theory37, the relationship between the viscosity and ΔGv is η = (h/vL)exp(ΔGv/kBT), where η is the viscosity and vL the volume of the unit of flow. Thus, the equilibrium jump frequency can be obtained

In our work, the viscosity of the PF is η = 0.90×10−2 Pa·s (see Supplementary Information 1) and the volume of the water molecule is vL = 34.22 Å3. We assumed that the adhesion energy contributing to the competition between the two PFs ΔGa = (ΔGa1+ΔGa2)/2, where ΔGa1 is the work of adhesion between a water molecule and the graphite and ΔGa2 is that between a water molecule and the graphene. Considering the Lennard-Jones (LJ) potential used in our simulations,

where ε = 0.15 kcal/mol and σ = 3.39 Å are the LJ parameters, ρv = 0.11 Å−3 and ρs = 0.38 Å−2 are the number of carbon atoms per unit volume of graphite and per unit area of graphene, respectively, h1 = 2.91 Å and h2 = 3.39 Å are the equilibrium distance between a water molecule and graphite and that between a water molecule and graphene, respectively. By substituting all the parameters into equation (3), ΔGa = (ΔGa1+ΔGa2)/2 = 2.00 kcal/mol. Then, after obtaining κ0 = 0.47 ns−1 from equation (2), the energy barrier could be derived by ΔGm = kBTln(kBT/κ0h) = 5.66 kcal/mol. So the energy dissipation from the viscosity ΔGv = ΔGm−ΔGa = 3.66 kcal/mol. From the data obtained, ΔGv > ΔGa, which illustrated that the energy was mainly dissipated by the viscosity. If we regarded the energy barrier as the height of the potential well above the substrate, the effective equilibrium distance between the PF and the substrate he = 2.63 Å (see Supplementary Information 2). The potential surface was scanned at he above the substrate as shown in Fig. 5c.

Using w2−w1 and κ0, we obtained the velocity from equation (1). But this velocity was not the wave velocity, because w2−w1 also contained the energy that drove the expanding spreading of the PFs and the energy stored in the graphene wrinkle. So we removed this part by subtracting the velocity function, which fitted from the part of the velocity after 0.14 ns when the wave frozen. Then the wave velocity function was obtained. The theory proposed here agreed qualitatively with the simulations as shown in Fig. 6. The deviation was due to the fact that MKT was a quasi-static theoretical model. Other factors, i.e., the PF which was not spreading in the wave direction, the effect of the graphene on the PF and etc, were not considered in this theory. The velocity graph plotted here also corresponded to the four stages (Fig. 2) illustrated in the results part.

Figure 6
figure 6

The capillary wave velocity obtained from MD simulations and MKT, respectively.

The inset shows the corresponding stage of the wave propagation.

Full size image

Using the scaling theory41 from the view of energy equilibrium, we derived the dispersion relation of the capillary wave to evaluate the phase velocity. Newtonian fluid model was used and the flow was assumed to be incompressible. For the whole system, the energy generated by the driving work difference Δw = w2−w1 equaled the energy dissipated viscously by the PF. Equating the energy input and dissipation, we obtained the dispersion relation of the wave (see Supplementary Information 3)

where k = 2π/λ is the wave number, d0 the thickness of the PF, η the viscosity of the PF and h the amplitude of the wave. Then the phase velocity of the wave42 was derived

If the dispersion effect was not considered, the relation λ = 2π/k = 2πd02/h must be satisfied. So equation (5) could be further simplified to

This equation illustrated that the propagation of the wave was driven by the competition between Δw and the viscosity. Equation (6) had the same form with the capillary velocity γ/η43, which described the competition between surface tension and viscosity without electric field.

The phase velocity calculated from equation (6) was the average wave velocity. So the driving work difference Δw (Fig. 5b) should also be averaged over time to evaluate the wave velocity from equation (6). Without loss of generalization, Δw was averaged from 0 ns to 0.05 ns of the first stage, during which the wave propagated along the negative direction. . On the other hand, the viscosity of the PF was η ~ 10−2 Pa·s (see Supplementary Information 1). From equation (6), the average wave velocity was obtained to be of the order of 100 m/s, which had the same order with that (~ 86.07 m/s) from the MD results. We also noticed that the capillary velocity of the bulk water without electric field was γ/ηw ~ 100 m/s. Besides, from the dispersion relation of the capillary wave without electric field, the wave velocity v = (γk/ρ)1/2 ~ 100 m/s, where k ~ 109 m−1, ρ = 1000 kg/m3.

The analysis above was based on the EEC process under E = 3 V/nm. However, we found that if only E was larger than a critical value (approximately 1 V/nm), PF2 could drill into the confined space between the graphene and the substrate and compete with PF1 to form the capillary wave (Fig. 4b). To explore the relation between the capillary wave velocity and E, we had done a series of EEC simulations under different E. Table 1 showed the change of the average wave velocity with respect to E. Interestingly, the capillary wave velocity was insensitive to E. In addition, we also found the propagation of the capillary wave in another EEC model, in which one end of the graphene was fixed (see Supplementary Information 5).

Table 1 The average capillary wave velocity v with respect to the electric field intensity E
Full size table

Previous discussions were based on MD simulations with periodic boundary condition (PBC). Although the PBC has the advantage that it is efficient, it has the defect that the periodic system would interact at the boundary. So is the wave cased by the PBC and strongly dependent on the boundary? To address this question, we have established another model in Supplementary Information 9. In this model, the boundary condition was set to be non-periodic and the substrate large enough to ensure that the boundary had little impact on the graphene-water system. In addition, the simulation box was set to be larger than the substrate. We not only found the capillary wave in this model, but also calculated the wave velocity to be of the order of 100 m/s. Therefore, the wave reported in this paper was not induced by the PBC, but by the competition between two PFs as was illustrated above. And the wave velocity was insensitive to the boundary.

In summary, the capillary wave propagation at nanoscale, induced by the competition between two PFs during EEC, was found and studied for the first time. During this process, the PF could separate the graphene from the substrate by EW between the graphene and the substrate driven by the Maxwell stress. This phenomenon can be a prospect candidate for delaminating graphene. From the atomic level, we developed MKT to describe the competition between two PFs. Then a scaling analysis was carried out to obtain the dispersion relation and average wave velocity. The theory showed that the competition between two PFs was controlled by their driving work difference originating from the disjoining pressure and the viscosity took priority in the energy dissipation. Simulating the EEC process under different E and different boundary conditions, the capillary wave velocity was found insensitive to E and the boundary. In addition, multilayer PFs were found during EEC (see Supplementary Information 4). The behavior of the PFs obeyed the power law with respect to time. The friction on the PF was larger than that on the substrate. We hope this work could provide valuable guidance for utilizing the PF to unwrap the folding structure or delaminate graphene from substrate.

Methods

MD simulations implemented in LAMMPS44 were carried out in this article. Water molecules and carbon atoms were modeled as LJ particles with truncated Coulomb potential interaction if charged

where εij is the potential well depth when there are no charges, σij the distance at which the LJ potential is zero, C the Coulomb constant, qi and qj the charges on the two atoms, r the distance between i and j atoms. The LJ and Coulomb cutoff were set to be 10 Å and 9.5 Å, respectively. The LJ parameters came from the consistent valence force-field (cvff)45, which is based on the experimental values and ab initio calculations. The interactions between water molecules and carbon atoms were calculated by the Lorentz-Berthelot (LB) rule:

Moreover, we set the interaction between the graphene and the substrate by 1/100 smaller than the calculated values by equation (8), to avoid the graphene sticking to the substrate during EC. To evaluate the precision of the LJ potential parameterized by the LB rule for simulating graphene-water interfacial dynamics, we have performed density functional theory simulations in Supplementary Information 8 for making a comparison. The results showed that the LJ potential parameterized by the LB rule could simulate the interactions between graphene and waters within acceptable precision.

The extended single point charge (SPC/E) water model46 was used. The SPC/E model was established by adding an average polarization correction to the single point charge (SPC) model, with a modified value of qO (charge on oxygen atom) and qH (charge on hydrogen atom). Compared with SPC, transferable intermolecular potential 3 point (TIP3P), transferable intermolecular potential 4 point (TIP4P) and transferable intermolecular potential 5 point (TIP5P) water model, SPC/E model predicts a better density, diffusion coefficient, surface tension and viscosity, which govern the EEC process, compared to the experimental values.

In order to model the electric field, the first layer of the graphite and the above graphite layer were charged with positive and negative charges, respectively, as shown in Fig. 1c. The field intensity could be calculated by E = Q/(Aε0ε) along the z direction, where Q, A, ε0 and ε represent the charges on each layer, the area of the layer, the vacuum permittivity and the relative permittivity of water, respectively. The calculated electric field intensity was E ~ 1 V/nm.

The whole system was modeled in NVT ensemble with Nose/Hoover method at 300 K and the time step was 1 fs. The boundary was periodic in three dimensions. And the box size was 30 nm × 30 nm × 30 nm. The droplet diameter was 8 nm containing 8904 water molecules (Fig. 1c). At the initial state, the graphene was placed on the center of the substrate, then the water droplet on the graphene. The substrate was fixed during the whole process. After relaxing for 0.1 ns, the droplet was wrapped by the graphene. Then we applied the electric field. The whole EEC process was simulated for 0.8 ns. The same process under different field intensities was repeated.