Abstract
Currently, the available algorithms for unbiased structure searches are primarily atom-based, where atoms are manipulated as the elementary units and energy is used as the target function without any restrictions on the bonding of atoms. In fact, in many cases such as nanostructure-assembled materials, the structural units are nanoclusters. We report a study of a bonding-restricted structure search method based on the particle swarm optimization (PSO) for finding the stable structures of two-dimensional (2D) materials containing dispersed C2 dimers rather than individual C atoms. The C2 dimer can be considered as a prototype of nanoclusters. Taking Si-C, B-C and Ti-C systems as test cases, our method combined with density functional theory and phonon calculations uncover new ground state geometrical structures for SiC2, Si2C2, BC2, B2C2, TiC2 and Ti2C2 sheets and their low-lying energy allotropes, as well as their electronic structures. Equally important, this method can be applied to other complex systems even containing f elements and other molecular dimers such as S2, N2, B2 and Si2, where the complex orbital orientations require extensive search for finding the optimal orientations to maximize the bonding with the dimers, predicting new 2D materials beyond MXenes (a family of transition metal carbides or nitrides) and dichalcogenide monolayers.
Similar content being viewed by others
Introduction
Determining the geometrical structures is essential to design new materials. The traditional X-ray diffraction technique for determining the crystal structure requires high quality samples and is incapable of dealing with materials under extreme conditions such as high pressure, strong electric or magnetic fields. On the other hand, determining a ground-state geometry based on chemical and physical intuitions is difficult due to the complex potential energy surface especially for materials with large unit cells or complicated structural units. Hence many structure prediction methods based on quantum mechanical simulations combined with global optimization algorithms have been developed, such as simulated annealing1, genetic algorithm2,3 and basin hopping4. However, in these currently available methods, energy is used as the target function and there are no restrictions on the bonding of atoms and atoms are usually manipulated as the elementary units. Thus, they are unsuitable for doing structure search for nanocluster-assembled materials where the structural units are nanoclusters, which are not directly bonded to each other but through linkers in most cases. Therefore, it is highly desirable to develop new search algorithms for doing such bonding-restricted structure search. An earlier work reported a constrained evolutionary search algorithm that enables prediction of polymeric crystal5. However, algorithms for motif-based prediction of low dimensional materials are not yet reported.
In this study, we report a dimer-based bonding-restricted search method for finding stable 2D structures with a restriction of no direct bonding between the dimers. C2 is a well-known pseudohalogen unit with an electron affinity of 3.4 eV6 and is the basic structural unit of diverse carbon compounds. It has received increasing attention due to its rich physical and chemical properties. R. Hoffmann7 recently made a comment on C2: “C2 is one of my favorite molecules, for this diatomic epitomizes many of the fundamental questions of chemistry”. Shaik and co-workers8 demonstrated that an unusual quadruple bond may exist in C2, which is strong enough to be considered as a typical chemical bond. In addition, dimerization of carbon is not only the first stage toward final crystallization, but also plays a vital role in the growth of many carbon related materials9,10. For instance, a C2 dimer on a Cu surface was identified as the dominant feeding species for graphene growth due to its lower diffusion and attachment barrier as compared to the carbon monomer and trimer11,12. Although the C2 dimer is quite chemically active and inclined to aggregate, it naturally occurs in the carbon vapor of interstellar medium and electric arcs. Vapor from a 16-V carbon arc was found to contain 28 wt% diatomic carbon13. As a result, in molecular dynamics (MD) simulations of growth of carbon–based materials, such as graphene, carbon nanotube and C60, C2 dimers are usually adopted as the initial carbon source14,15,16.
Furthermore, the C2 dimer is the building block of metal-alkynide complexes17, alkynide complexes18, metallocarbohedrenes clusters MmCn19,20 (usually termed as metcars) and ternary metal carbides (LiAgC2, KAgC2, CsAgC2 and NaPdC2)21. In recently studied silicon carbides (SixCy), the dimerization of C in the SiC monolayer reintroduces the Dirac cone into the honeycomb lattice22, while SiC sheets without C2 dimer are wide-band gap semiconductors23,24,25,26. In SiC2 silagraphene27, each silicon atom binds to four C2 units in a flat plane, resulting in a metallic sheet. When C2 dimers are embedded in a 2D porphyrin sheet, the system becomes highly active for oxygen reduction reaction28. In addition, it was demonstrated that the formation of C2 dimers plays an important role in stabilizing metcar clusters29.
Due to the C2 dimer’s unique properties as well as its importance in forming numerous carbon-based three-dimensional materials and zero-dimensional nanostructures, we focus this study on developing a dimer-based global search algorithm to design 2D materials containing dispersed C2 dimers to retain its intrinsic properties. We then apply this method to identify the ground state geometries of the 2D Si-C2, B-C2 and Ti-C2 systems containing C2 dimers as test cases.
Results and Discussion
To test our method, we applied it to three systems where C2 dimers are linked with Si, B and Ti atoms respectively. New ground state geometries and new low-lying isomers are identified.
2D Si-C2 system
Recently, SiC2 and Si2C2 sheets with dispersed carbon dimers have received some attention. The studies were carried out using a priori geometric structures to investigate the properties of 2D Si-C sheets22,27,30. However, a complete understanding of Si-C2 phases is still lacking and it is unclear whether the studied structures are the ground states under the condition of discrete C2 dimers. Thus we have conducted a comprehensive structure search to identify the ground state geometry and the low-lying energy isomers of the Si-C2 system.
The most stable structure of Si2C2 and three low-lying energy isomers of SiC2 have been identified using our C2 dimer-based global search. Because the lowest energy geometry of Si2C2 is found to be identical to a recently reported structure22, we only concentrate on the three isomers of the SiC2 sheet, as shown in Fig. 1. In these structures all carbon atoms are pairwisely bonded with each other and covalently bonded with Si atoms. They all are comprised of four-fold coordinated Si with three-fold coordinated C atoms. The structure, shown in Fig. 1(a), is composed of pure pentagons, thus it is named penta-SiC2. The other two isomers shown in Fig. 1(b,c) consist of 4-, 5- and 6-rings and 4- and 6-rings, respectively, labeled as 456-SiC2 and 46-SiC2 accordingly. Si-C and C-C bond lengths are about 1.90 Å and 1.36 Å respectively. The side views show the sandwich-like structures with the four-fold coordinated Si atoms in the middle sandwiched between C2 dimers. When we consider the Si sublattice and C2 dimer (treating C2 as a structural unit) sublattice separately, it turned out that the major difference among these three isomers is the orientation of C2 dimers, namely the dimers are parallel to each other in 46-SiC2, while they are perpendicular to each other in penta-SiC2 (In Supplementary Information, we shortly discuss the kinetic barriers connecting different isomers). It is obvious that the different arrangement of C2 dimers remarkably alters the geometrical structures, resulting in the different electronic properties of these isomers as demonstrated in the following paragraph.
Geometrical and electronic structures.
Top and side views of the atomic configurations of C2 dimer-based 2D SiC2 isomers and their corresponding electronic band structures. (a) penta-SiC2, (b) 456-SiC2 and (c) 46-SiC2. Grey and yellow spheres represent C and Si atoms, respectively. The relative energy/f.u. with respect to penta-SiC2 is given below each structure. Decomposed band structures (bottom panel) show the contribution of different orbitals.
Total energy calculations reveal that all three isomers are energetically more favorable than the previously proposed SiC2-silagraphene27 with planar tetracoordinate silicon atoms. Penta-SiC2, 456-SiC2 and 46-SiC2 are 0.63, 0.57 and 0.51 eV/formula unit (f.u.) lower in energy than that of SiC2-silagraphene, suggesting that the Si-C2 sheet is more likely to adopt a buckled structure with the partially sp3 hybridized Si and the sp2 hybridized C. Penta-SiC2 is found to be the lowest energy configuration among the three isomers with the Si-C and C-C bond lengths of 1.90 Å and 1.36 Å respectively, which is identical to that reported recently by Bezanilla et al.30 and as 456-SiC2 lies only 0.06 eV higher in energy than penta-SiC2, the two structures can be considered as energetically degenerate. The relative energy of 46-SiC2 with respect to penta-SiC2 is 0.12 eV. The dynamical stability of the predicted low-lying energy isomers of SiC2 is verified by calculating their phonon dispersions. The results plotted in Fig. S1 (see Supplementary Information) show that the three structures are all dynamically stable since their vibration modes are real in their entire Brillouin zones, respectively.
To understand the electronic properties of the three isomers, their band structures are calculated using the HSE06 hybrid functional. Furthermore, a more detailed investigation of the contribution from each atomic orbital to the band structure is carried out using the color-mapped bands. The calculated results are presented in Fig. 1, which shows that penta-SiC2, 456-SiC2 are large band gap compounds with band gaps of 3.1 eV, 2.7 eV, while the bandgap of 46-SiC2 is 0.55 eV. We note that 46-SiC2 is a direct band gap semiconductor and its band gap is much smaller than that of penta-SiC2 and 456-SiC2. While the others are indirect band gap semiconductors because the valence band maximum (VBM) and the conduction band minimum (CBM) are not at the same point in their Brillouin Zones. The localized distribution of pz orbitals of the C2 dimer, above and below the Fermi level, is disclosed in the colored band structure (red dot curves in decomposed band structure). Further analyses of the chemical bonding of the C2 dimer reveals that the localized distribution originates from the bonding and anti-bonding pz orbital of C2 dimers. Due to the unique geometrical structure, the alternation of partially sp3 hybridized Si and slightly distorted sp2 C prevents the pz orbitals from forming a delocalized π bond. This could explain, to some degree, why these pz composed bands are less dispersive than those in graphene or other planar silicon carbon sheets.
To understand the origin of the different electronic structures exhibited in the three isomers, the detailed structural configurations of the local C and Si atoms in penta-SiC2 and 46-SiC2 are sketched in Fig. S3 (see Supplementary Information). Penta-SiC2 has higher symmetry subjecting it to the least geometrical distortion among the three isomers. 46-SiC2’s parallel arrangement of the C2 dimer imposes a larger geometrical distortion; the angle of C with its neighboring Si is 92.9 °, while that in penta-SiC2 is 109.6 °. The Si atoms in 46-SiC2 also adopt the distorted hybridization as compared to that in penta-SiC2. Besides, the decomposed band structures (Fig. 1) show that the highest and the second highest occupied bands near the M point in 46-SiC2 are exclusively from the Si-C σ bonds. The larger geometrical distortion of Si-C σ bonds in 46-SiC2 leads to a stronger interaction between the relevant orbitals, resulting in the highly dispersive bands and a smaller band gap.
2D B-C2 system
For the second test system, we study the 2D B-C2 system due to boron’s rich chemistry: for example its electron deficiency and versatile bonding ability. In fact, nanostructures composed of boron and carbon atoms have attracted growing interest both theoretically and experimentally. For instance, a BC3 honeycomb structure with high crystalline quality was identified by electron diffraction31. A B2C sheet with planar tetra-coordinated carbon (pt-C) moiety was theoretically predicted32. A thorough study of B-C compounds with different stoichiometry was carried out by performing a PSO search33. However, a study on B-C sheets comprised of discrete C2 dimers has not been reported. Due to its versatility in forming various chemical bonds and the differing chemical nature of B from Si, the bonding between B and the C2 dimer is expected to be quite different from that of Si and C2, leading to B-C2 systems with different structural and electronic properties.
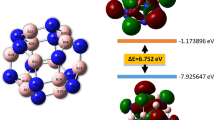
Using our dimer-based search algorithm, three low-lying energy isomers of B2C2 and one stable structure of BC2 are obtained (Fig. 2). Geometry optimizations and total energy calculations suggest that the structure shown in Fig. 2(a1) has the lowest energy of the three isomers of B2C2 with a total energy of 0.04 eV, 0.13 eV lower than that of the structures shown in Fig. 2(a2,a3), respectively. To examine the dynamical stability of these structures, we calculated their phonon dispersions. The results are plotted in Fig. S4. The absence of imaginary modes in the entire Brillouin zone for each of the structures confirms that they are all dynamically stable. However, we note that these structures are energetically metastable as compared to the B-C planar monolayers predicted by Luo et al. (B2C2-a is 0.23 eV/f.u. higher in energy than the most stable BC sheet).
In order to gain more insight into the chemical bonding in the B-C2 sheets, we plotted an electron localization function (ELF)34 isosurface (with a relatively large isovalue of 0.75 to reflect the σ bonds between the atoms) in Fig. 3. According to the ELF diagrams, carbon in B2C2-a and B2C2-b adopt sp3 hybridization and each carbon atom is covalently bonded to three adjacent B and one C atoms. B atoms take a slightly distorted sp2 configuration. The C-C bond length in Fig. 2(a1,2) are 1.51 Å (close to that of a C-C single bond). While in B2C2-c, both the B and C atoms have sp2 hybridization. B2C2-c adopts a planar honeycomb structure similar to graphene35, however, the total energy of B2C2-c is 0.13 eV/f.u. higher than that of B2C2-a. Multi-center bonds are pretty common in boron-related materials36,37 and contribute a lot to their stability. However, no such bonds are found in B2C2-a, B2C2-b and B2C2-c, which might explain the physical origin of their higher energy.
For the BC2 sheet, only one stable structure without imaginary modes was discovered (Figs 2(b) and S4(b)). In particular, all the BC2 structures isostructural to those of SiC2 (namely penta-BC2 or 46-BC2) are unstable, reflecting the differing chemical nature of B and Si. In this highly buckled BC2 sheet (the thickness is 1.53 Å), all C atoms are strongly covalently bonded together; the C-C bond length is 1.31 Å. The calculated electron localization function (ELF) shows that there are sp3 hybridized B and nearly planar tetracoordinate B atoms. In our case, the bonding type of planar tetracoordinated B is closer to the case of planar tetracoordinated Si27 and C32.
Our electronic band structure calculations (Fig. 2) show that the ground state structures of B2C2 and BC2 with the discrete C2 dimers have indirect band gaps of 2.9, 2.8 and 4.1 eV at the HSE06 level for B2C2-a, B2C2-b and BC2, respectively, which is in contrast to the metallic BC sheet33 where C is not in C2 form. The reason is, once we restrict the carbon atoms to be pairwisely bonded together, the most stable structures (B2C2-a and BC2) discovered by using our dimer-based search are buckled. The separation of C2 dimers by boron atoms and the buckling nature of the sheets would destroy the delocalization of pz π electrons of boron and carbon (the main reason for the metallicity of many planar stable B-C compounds). In the B2C2-c isomer, the planar geometry, as well as its delocalized π electrons is preserved. Geometrically speaking, B2C2-c is similar to honeycomb SiC22. Since boron has few valence electrons it is impossible to fill all the electronic states below the Dirac cone giving rise to metallicity.
2D Ti-C2 system
To study the interaction between the C2 dimer and transition metal elements, we have systematically studied Ti-C2 sheets for the following reasons: (1) both Ti and Si possess four valence electrons, thus it is intriguing to look at the difference between TiC2 and SiC2 sheets and Ti2C2 and Si2C2 sheets. (2) Titanium and carbon have been found to form various kinds of stable compounds ranging from 0D clusters19,38, to 2D sheets39,40 and to 3D bulk materials. Among them, in metcar clusters all carbon atoms exist in the form of a C2 dimer19. Therefore, it might be possible to find a family of 2D crystals that consists of transition metal atoms and C2 dimers. (3) Recently, a group of 2D layered early transition metal carbides termed as MXenes, including Ti3C2 and Ti2C, were experimentally synthesized by exfoliation from their bulk MAX phases41,42,43. However, in MXenes sheets, C is in atomic form rather than a C2 dimer. Therefore it is necessary to study the possibility of forming stable 2D titanium carbides containing C atoms that are all in C2 dimer form.
We concentrated on the 2D titanium carbide sheets with the stoichiometry of TiC2 and Ti2C2 where C is in the form of a C2 dimer. Recently, a TiC2 sheet was predicted to have good performance as anode material for a lithium ion battery40. However, the geometrical structure was artificially designed. Thus, it is easy to miss some low-lying isomers. In fact, we found, using our dimer-based algorithm, that among the isomers of TiC2, there is a one that is lower in energy by 0.13 eV/f.u. than the recently reported structure40. In this lowest energy structure, as shown in Fig. 4(a), due to the different orientations of C2 dimers, the total thickness of 1.97 Å is less than the 2.02 Å of the reported structure40. One can see when going from Si to Ti, although both have four valence electrons, the complex 3d orbitals in Ti require a delicate arrangement of C2 dimers to match with the d orbital orientations for maximizing the interactions. The stability of the TiC2 sheet can be traced back to the most stable  -like Ti8C12 cluster44, where all carbon dimers bind to Ti in end-on configuration (EOC) and side-on configuration (SOC), which strengthens the bonding between Ti and C and stabilizes the Ti8C12 cluster. In our 2D TiC2 sheet EOC and SOC are apparently well preserved. The C-C bond length is 1.33 Å, which is slightly longer than that of a dispersed C2 molecule (1.31 Å) due to the partial occupation of πg orbital of C2 in TiC2. The bond length of Ti-C in EOC and SOC modes is 2.05 Å and 2.19 Å, respectively, close to 2.1 Å in Ti2C MXene phase.
-like Ti8C12 cluster44, where all carbon dimers bind to Ti in end-on configuration (EOC) and side-on configuration (SOC), which strengthens the bonding between Ti and C and stabilizes the Ti8C12 cluster. In our 2D TiC2 sheet EOC and SOC are apparently well preserved. The C-C bond length is 1.33 Å, which is slightly longer than that of a dispersed C2 molecule (1.31 Å) due to the partial occupation of πg orbital of C2 in TiC2. The bond length of Ti-C in EOC and SOC modes is 2.05 Å and 2.19 Å, respectively, close to 2.1 Å in Ti2C MXene phase.
Geometrical and electronic structures.
Top and side views of the crystal structures of (a) TiC2, and (b) Ti2C2 and their corresponding electronic band structures and partial DOS. Magenta and grey spheres represent Ti and C atoms, respectively. Their dynamical stabilities are confirmed by phonon calculations (see Fig. S5 in Supplementary Information).
We then increased the atomic ratio of Ti from TiC2 to Ti2C2 to study the effect of Ti concentration on the geometry and properties of the Ti-C sheets. The structure shown in Fig. 4(b) is found to have the lowest energy among the isomers of Ti2C2 under the requirement of discrete C2 dimers and it lies lower in energy by 0.25 eV/f.u than the t-TiC sheet39. This suggests that when the same atomic ratio of Ti to C exists, C2 is energetically more favorable than atomic C to bind with Ti in forming a sheet. The C-C bond length is 1.48 Å, close to that of C-C single bond but longer than that in a TiC2 sheet. This is because the hybridization between the C2-πg and Ti-3d is stronger in Ti2C2, resulting in more πg states being occupied, thus leading to the elongated C-C bond.
The calculated band structures and partial DOS are also plotted in Fig. 4, which clearly show that the TiC2 sheet is metallic, while the Ti2C2 sheet, like the t-TiC sheet, is an indirect narrow gap semiconductor with a gap of 0.1 eV at the HSE06 level. It is known that the ground state electronic configuration of an dispersed C2 is (1σg)2(1σu)2(2σg)2(2σu)2(1πu)4 with the higher energy states (3σg)(1πg)(3σu) unoccupied and the (2σg)2(2σu)2(1πu)4(3σg) having much lower energy as compared to the orbitals of Ti-3d. Therefore, a weak interaction between the deep level orbitals of C2 and Ti-3d is expected. Thus, the electronic states near the Fermi level are mainly from the interplay between C2-πg and Ti-3d orbitals.
For the structure of t-TiC39 a strong electronic resonance between C-2p and Ti-3d is obvious. Due to the strong hybridization between C-2p and Ti-3d and the low buckled geometry of t-TiC, the bonding states of C-2p and Ti-3d are separated from the unoccupied Ti-3d states forming a band gap. TiC2 is geometrically analogous to t-TiC with carbon atoms replaced with discrete C2 dimers. However, replacing C with C2 leads to drastic change in their electronic structures, namely t-TiC is semiconducting with a strong electronic resonance, while TiC2 is metallic. This is because the πg orbitals of C2 hybridize with the Ti-3d orbitals, forming the energy bands crossing the Fermi level, thus, resulting in metallicity of TiC2. For the Ti2C2 sheet, the electronic states near the Fermi level are also derived from C2 πg and Ti 3d orbitals similar to TiC2, yet the interaction between C2 πg and Ti 3d orbitals is stronger as compared to that in TiC2 due to the higher Ti concentration, which reduces the electronic states near the Fermi level and thus results in the small band gap as shown in Fig. 4(b).
Based on the above discussions, the following intriguing points can be concluded: (1) compared with the sandwiched structure of the TiC2 sheet, the Ti atoms are more exposed in the Ti2C2 sheet and hence have higher chemical reactivity; (2) Although having a higher atomic ratio of Ti, the Ti2C2 sheet is semiconducting with a band gap of 0.1 eV, while the TiC2 sheet is metallic; (3) For the t-TiC39 and Ti2C2 sheets, although they have the same composition ratio, when going from atomic C to C2 dimer, the band gap is reduced from 0.2 eV to 0.1 eV, showing promising applications of the Ti2C2 sheet in infrared light-related technology.
Summary
In this study, we developed a dimer-based bonding-restricted structure search method to find the ground state structures of the 2D materials containing C2 dimers with a restriction of no direct bonded dimers and then applied this method to three systems composed of discrete C2 dimers that are coordinated with Si, B and Ti atoms, respectively, as test cases. For the SiC2 sheet, three energetically nearly degenerate allotropes with very different electronic structures are identified, which also differ from the previously proposed SiC2-silagraphene27, showing that tuning the orientation of the C2 dimers not only can modulate the size of the band gap, but also can induce the transition from an indirect gap to a direct gap. For the B-C system, the ground state structures of both BC2 and B2C2 sheets are determined. Due to the different chemical nature of B and Si, all the possible structures of BC2 isostructural to those of SiC2 are unstable. In the ground state configuration of BC2, each C2 dimer is bonded with three B atoms forming a 2D sheet with a thickness is 1.53 Å and a band gap of 4.1 eV. When increasing the number of atomic B to form B2C2, each C2 dimer is bonded to six B atoms having the maximum number of B-C σ bonds and reducing the band gap to 2.9 eV. Unlike the metallic BC sheet33 where C atoms do not form any dimers, both the BC2 and B2C2 sheets identified here are semiconducting. The emergence of band gap is attributed to the buckled structures, which prevents the delocalization of pz orbitals. For the Ti-C system, a new structure of the TiC2 sheet with a lower energy than the metallic TiC2 sheet reported recently40 was found. A Ti2C2 sheet was also found to be energetically more stable than the previously proposed t-TiC sheet39, suggesting it is more favorable for Ti to bind with C2 dimers in forming 2D structures. Unlike the metallic TiC2 monolayer40, the Ti2C2 sheet is an indirect band gap semiconductor. In addition, compared with the structures composed of C2 dimers and nonmetallic elements (Si, B), both the stable TiC2 and Ti2C2 sheets adopt relatively more compact structures due to the complex orientations of d orbitals, which require a more extensive search to find the optimal orientation of the C2 dimers. These cases show that our searching algorithm is efficient and indispensable to design new 2D materials beyond the atom-based ones.
Methods
Dimer-based search algorithm
Particle Swarm Optimization (PSO), one of the most popular swarm intelligence algorithms, was originally developed by Kennedy and Eberhart in 199545. The PSO algorithm utilizes the collective intelligence of the whole population rather than a single individual, it is quite efficient in handling various optimization problems. Recently, the PSO algorithm has been successfully applied to crystal structure prediction46,47,48, another intractable optimization problem. Just like in the natural world where collective intelligence facilitates the locating of food or optimal habitats for insects and fishes, PSO implementation in CALYPSO was proven to be efficient in predicting the most stable structures for undiscovered materials48.
Due to the great success of PSO in predicting crystal structures, we have studied a dimer-based structure search program based on the PSO algorithm, where additional constraints and augmented algorithm are added. The main framework of our dimer-based structure search method is illustrated by the flowchart as shown in Fig. 5.
Before outlining the details of the steps given in the flowchart, we will explain the treatment of the C2 dimer in our constrained search method. The requirements are that all carbon atoms exist in the form of a C2 dimer and each dimer must be separated from the others. A C2 dimer can be treated naturally as a “pseudo-atom”. However, general treatments for ordinary atoms are not sufficient for “pseudo atoms”, as an ordinary atom is treated as an isotropic sphere, while a C2 dimer is considered a pseudo atom exhibiting structural anisotropy along the molecular axis. Therefore, to fully represent a C2 dimer, extra indices are imperative. As shown in Fig. 6, besides the three coordinates, x, y and z, the dimeric orientation angles φ and θ are required. Therefore, in our augmented PSO algorithm, the coordinates needed are ri = (xi, yi, zi, φi, θi), where xi, yi and zi are used to denote the barycenter, φi and θi are used to represent the orientation of the dimer. Besides, during the PSO-based structure searches, the bond length of C2 dimer is allowed to vary within the length of C-C single and triple bond. Accordingly, the PSO algorithm is modified to accommodate these changes.
There are four main steps enumerated in the flowchart, some operative techniques are directly adapted from previous works46,48. First of all, most of the trial structures are partially randomly generated under symmetry restrictions46,49,50 or evolved via the PSO algorithm48,51. Fully randomly generated structures are also used. The reason is in 2D space there are 17 plane groups overall belonging to four different crystallographic systems (oblique, rectangular, square and hexagonal); one of the groups is selected each time to create a new trial structure. The lattice shape of the new structure is determined by the selected space group and its area. Generally, the positions of the atoms or the barycenter of C2 dimer are allocated on Wyckoff positions for the chosen plane group. An extra step is needed to generate bond length and orientation for each dimer randomly or partially restricted, which is different from atom-based structure prediction methods. All these steps are sketched in Fig. 7. In order to predict 2D materials with finite thickness, the coordinate zi of atoms and dimers are assigned randomly within a thickness Δ as shown in Fig. 7(d). However, because the number of 2D plane groups is finite, the generating method for a symmetry constrained structure is prone to produce similar structures. In this case totally randomly generated structures are needed to guarantee the diversity of structures.
Another source of the new trial structures is the PSO evolution which is a population-based algorithm. The population in our case is defined as a group of structures. For generation t, we define a population Pt and every structure in generation t is represented as a particle Pit. The evolution of structures is controlled by PSO algorithm:

where i and t are indexes of particle (structure) and generation,  represents the structural information of a certain structure including the orientation of dimers and the coordinates of atoms,
represents the structural information of a certain structure including the orientation of dimers and the coordinates of atoms,  is the velocity or rate of structural change of certain structure i. The velocity of structure i is calculated as follows:
is the velocity or rate of structural change of certain structure i. The velocity of structure i is calculated as follows:

where ω is the inertia weight and controls the momentum of the particle,  is the optimized structure of particle i and
is the optimized structure of particle i and  is the structure with the lowest energy obtained so far for generation t, r1 and r2 are two random numbers uniformly distributed in range [0, 1], c1 and c2 are set to be 247,52. The definition of velocity fully reflects the idea of collective intelligence. The trajectory of each particle is biased, to a certain degree, toward the best structure of whole population and itself at the same time.
is the structure with the lowest energy obtained so far for generation t, r1 and r2 are two random numbers uniformly distributed in range [0, 1], c1 and c2 are set to be 247,52. The definition of velocity fully reflects the idea of collective intelligence. The trajectory of each particle is biased, to a certain degree, toward the best structure of whole population and itself at the same time.
The three structure generation approaches work synergistically and serve different purposes during the structure search. The partially random structure generation with symmetry constraints help reduce the degree of freedom and narrow the search space. The fully random structure generation warrants the structural diversity and the PSO-based structure evolution provides an effective way to explore the configuration space and locate the thermodynamically favorable structures.
It is important to note here that due to the nonequivalent coordinates xi, yi, zi and φi, θi in terms of their magnitudes and range, C2 dimers and ordinary atoms must be manipulated separately. In addition, the newly generated trial structures must satisfy the condition that all C2 dimers are disconnected from each other, thus the structures with dimer clustering are eliminated. Next, similarities between the different structures are examined. Each structure is characterized by a set of predetermined fingerprinting functions48,52 and the distance between two structures are calculated based on the difference of their fingerprinting functions. If a newly produced structure is similar to the previous one, the new structure is discarded. Finally, local structure optimization is performed to drive the structure to the local minimum on multi-dimensional energy space, which also provides physical and rational structures for future PSO evolution.
First principles calculation
Combined with our bonding-restricted algorithm, first principles calculations within the framework of density functional theory (DFT) are performed for local geometry optimizations during structure search. Calculations are mainly performed by using the Vienna Ab initio Simulation Package (VASP)53. The Perdew-Burke-Ernzerhof (PBE) functional54 is used to incorporate the exchange-correlation interaction. The HSE06 hybrid functional55,56 is used for high accuracy of electronic structure calculations. The projector augmented wave (PAW)57 method is used to treat the interactions between ion cores and valance electrons. Plane waves are used to expand the valance electron (2s22p1 for B, 2s22p2 for C, 3s23p2 for Si and 3d34s1 for Ti) wave functions. During the massive structure searching stage, in order to reduce the workload, plane waves with a kinetic energy cutoff of 350 eV and Monkhorst-Pack scheme with a sparse grid density (2π × 0.04 Å−1) are adopted. To compare the relative stability of different candidate structures, we used the same kinetic energy cutoff, k-point grid density and exchange-correlation functionals to perform geometry optimizations and total energy calculations. Plane waves with a kinetic energy cutoff of 450 eV and Monkhorst-Pack scheme58 with a grid density of 2π × 0.02 Å−1 are used to optimize the structures and calculate their electronic properties. The convergence criteria for total energy and forces are set to be 10−4 eV and 10−3 eV/Å, respectively. The supercell approach is used to calculate force constants. A vacuum space of 20 Å in the perpendicular direction is added to avoid the interaction between periodic images. Phonon properties are calculated using the finite displacement method as implemented in the Phonopy package59,60.
Additional Information
How to cite this article: Zhang, C. et al. Bonding-restricted structure search for novel 2D materials with dispersed C2 dimers. Sci. Rep. 6, 29531; doi: 10.1038/srep29531 (2016).
References
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. Optimization by Simulated Annealing. Science 220, 671–680 (1983).
Abraham, N. & Probert, M. A periodic genetic algorithm with real-space representation for crystal structure and polymorph prediction. Phys. Rev. B 73, 224104 (2006).
Trimarchi, G. & Zunger, A. Global space-group optimization problem: Finding the stablest crystal structure without constraints. Phys. Rev. B 75, 104113 (2007).
Wales, D. J. & Doye, J. P. K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 101, 5111–5116 (1997).
Zhu, Q., Sharma, V., Oganov, A. R. & Ramprasad, R. Predicting polymeric crystal structures by evolutionary algorithms. J. Chem. Phys. 141, 154102 (2014).
Cederbaum, L., Domcke, W. & Von Niessen, W. Many-body calculation of electron affinities: C2 and a prediction for P2 . J. Phys. B 10, 2963 (1977).
Shaik, S., Rzepa, H. S. & Hoffmann, R. One molecule, two atoms, three views, four bonds? Angew. Chem. Int. Ed. 52, 3020–3033 (2013).
Shaik, S. et al. Quadruple bonding in C2 and analogous eight-valence electron species. Nat. Chem. 4, 195–200 (2012).
Wang, Q., Ng, M.-F., Yang, S.-W., Yang, Y. & Chen, Y. The mechanism of single-walled carbon nanotube growth and chirality selection induced by carbon atom and dimer addition. ACS Nano 4, 939–946 (2010).
Sternberg, M., Zapol, P. & Curtiss, L. A. Carbon dimers on the diamond (100) surface: Growth and nucleation. Phys. Rev. B 68, 205330 (2003).
Wu, P. et al. Carbon Dimers as the Dominant Feeding Species in Epitaxial Growth and Morphological Phase Transition of Graphene on Different Cu Substrates. Phys. Rev. Lett. 114, 216102 (2015).
Riikonen, S., Krasheninnikov, A., Halonen, L. & Nieminen, R. The Role of Stable and mobile carbon adspecies in copper-promoted graphene Growth. J. Phys. Chem. C. 116, 5802–5809 (2012).
Skell, P. S. & Plonka, J. H. Chemistry of the singlet and triplet C2 molecules. Mechanism of acetylene formation from reaction with acetone and acetaldehyde. J. Am. Chem. Soc. 92, 5620–5624 (1970).
Artyukhov, V. I., Liu, Y. & Yakobson, B. I. Equilibrium at the edge and atomistic mechanisms of graphene growth. Proc. Natl. Acad. Sci. 109, 15136–15140 (2012).
Artyukhov, V. I., Penev, E. S. & Yakobson, B. I. Why nanotubes grow chiral. Nat. Commun. 5, 4892 (2014).
Irle, S., Zheng, G., Elstner, M. & Morokuma, K. From C2 molecules to self-assembled fullerenes in quantum chemical molecular dynamics. Nano Lett. 3, 1657–1664 (2003).
Long, N. J. & Williams, C. K. Metal Alkynyl σ Complexes: Synthesis and Materials. Angew. Chem. Int. Ed. 42, 2586–2617 (2003).
Yam, V. W.-W. Molecular Design of Transition Metal Alkynyl Complexes as Building Blocks for Luminescent Metal-Based Materials: Structural and Photophysical Aspects. Accounts. Chem. Res. 35, 555–563 (2002).
Guo, B., Kerns, K. & Castleman, A. Jr. Ti8C12+-Metallo-Carbohedrenes: A New Class of Molecular Clusters? Science 255, 1411 (1992).
Rohmer, M.-M., Bénard, M. & Poblet, J.-M. Structure, reactivity and growth pathways of metallocarbohedrenes M8C12 and transition metal/carbon clusters and nanocrystals: A challenge to computational chemistry. Chem. Rev. 100, 495–542 (2000).
Buschbeck, R., Low, P. J. & Lang, H. Homoleptic transition metal acetylides. Coordin. Chem. Rev. 255, 241–272 (2011).
Qin, X. et al. Origin of Dirac Cones in SiC Silagraphene: A Combined Density Functional and Tight-Binding Study. J. Phys. Chem. Lett. 6, 1333–1339 (2015).
Sun, X.-H. et al. Formation of silicon carbide nanotubes and nanowires via reaction of silicon (from disproportionation of silicon monoxide) with carbon nanotubes. J. Am. Chem. Soc. 124, 14464–14471 (2002).
Bekaroglu, E., Topsakal, M., Cahangirov, S. & Ciraci, S. First-principles study of defects and adatoms in silicon carbide honeycomb structures. Phys. Rev. B 81, 075433 (2010).
Zhao, K., Zhao, M., Wang, Z. & Fan, Y. Tight-binding model for the electronic structures of SiC and BN nanoribbons. Physica. E 43, 440–445 (2010).
Gori, P., Pulci, O., Marsili, M. & Bechstedt, F. Side-dependent electron escape from graphene-and graphane-like SiC layers. Appl. Phys. Lett. 100, 043110 (2012).
Li, Y., Li, F., Zhou, Z. & Chen, Z. SiC2 silagraphene and its one-dimensional derivatives: where planar tetracoordinate silicon happens. J. Am. Chem. Soc. 133, 900–908 (2010).
Li, Y. et al. A new C = C embedded porphyrin sheet with superior oxygen reduction performance. Nano. Res. 8, 2901–2912 (2015).
Joswig, J.-O. & Springborg, M. The influence of C2 dimers on the stability of TimCn metcar clusters. J. Chem. Phys. 129, 134311–134311 (2008).
Lopez-Bezanilla, A. & Littlewood, P. B. σ–π-Band Inversion in a Novel Two-Dimensional Material. J. Phys. Chem. C. 119, 19469–19474 (2015).
Kouvetakis, J., Kaner, R. B., Sattler, M. L. & Bartlett, N. A novel graphite-like material of composition BC3 and nitrogen-carbon graphites. J. Chem. Soc., Chem. Commun. 1758–1759 (1986).
Wu, X., Pei, Y. & Zeng, X. C. B2C graphene, nanotubes and nanoribbons. Nano Lett. 9, 1577–1582 (2009).
Luo, X. et al. Predicting two-dimensional boron–carbon compounds by the global optimization method. J. Am. Chem. Soc. 133, 16285–16290 (2011).
Silvi, B. & Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 371, 683–686 (1994).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Tang, H. & Ismail-Beigi, S. Novel precursors for boron nanotubes: the competition of two-center and three-center bonding in boron sheets. Phys. Rev. Lett. 99, 115501 (2007).
Galeev, T. R. et al. Deciphering the mystery of hexagon holes in an all-boron graphene α-sheet. Phys. Chem. Chem. Phys. 13, 11575–11578 (2011).
Wei, S. & Guo, B. Metallo-carbohedrenes: Formation of multicage structures. Science 256, 818–820 (1992).
Zhang, Z., Liu, X., Yakobson, B. I. & Guo, W. Two-dimensional tetragonal TiC monolayer sheet and nanoribbons. J. Am. Chem. Soc. 134, 19326–19329 (2012).
Zhao, T., Zhang, S., Guo, Y. & Wang, Q. TiC2: a new two-dimensional sheet beyond MXenes. Nanoscale 8, 233–242 (2016).
Naguib, M., Mochalin, V. N., Barsoum, M. W. & Gogotsi, Y. 25th Anniversary Article: MXenes: A New Family of Two-Dimensional Materials. Adv. Mater. 26, 992–1005 (2014).
Naguib, M. et al. Two-dimensional transition metal carbides. ACS Nano 6, 1322–1331 (2012).
Naguib, M. et al. Two-Dimensional Nanocrystals: Two-Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2 . Adv. Mater. 23, 4207–4207 (2011).
Berkdemir, C., Castleman, A. & Sofo, J. O. Metal-substituted Ti8C12 metallocarbohedrynes: toward less reactive clusters as building blocks of cluster-assembled materials. Phys. Chem. Chem. Phys. 14, 9642–9653 (2012).
Kennedy, J. In Encyclopedia of Machine Learning 760–766 (Springer, 2010).
Wang, Y. & Ma, Y. Perspective: Crystal structure prediction at high pressures. J. Chem. Phys. 140, 040901 (2014).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wu, S. et al. An adaptive genetic algorithm for crystal structure prediction. J. Phys. Condens. Matter 26, 035402 (2014).
Liu, Z.-L. MUSE: Multi-algorithm collaborative crystal structure prediction. Comput. Phys. Commun. 185, 1893–1900 (2014).
Call, S. T., Zubarev, D. Y. & Boldyrev, A. I. Global minimum structure searches via particle swarm optimization. J. Comput. Chem. 28, 1177–1186 (2007).
Gao, B., Shao, X., Lv, J., Wang, Y. & Ma, Y. Structure Prediction of Atoms Adsorbed on Two-Dimensional Layer Materials: Method and Applications. J. Phys. Chem. C. 119, 20111 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Erratum: “Hybrid functionals based on a screened Coulomb potential”. J. Chem. Phys. 124, 219906 (2006).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scripta Mater. 108, 1–5 (2015).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Acknowledgements
This work is partially supported by grants from the National Natural Science Foundation of China (NSFC-51471004), the National Grand Fundamental Research 973 Program of China (Grant No. 2012CB921404) and the Doctoral Program of Higher Education of China (20130001110033). The calculations were carried out at the National Supercomputer Center in Guangzhou, China.
Author information
Authors and Affiliations
Contributions
Q.W. designed the project; C.Z. performed the calculations; C.Z., S.Z. and Q.W. analyzed the results and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, C., Zhang, S. & Wang, Q. Bonding-restricted structure search for novel 2D materials with dispersed C2 dimers. Sci Rep 6, 29531 (2016). https://doi.org/10.1038/srep29531
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep29531
This article is cited by
-
Linear and elliptical photogalvanic effects in two-dimensional penta-BP5 photodetector
Applied Physics A (2024)
-
Symmetry-protected metallic and topological phases in penta-materials
Scientific Reports (2019)
-
Origins of Dirac cone formation in AB3 and A3B (A, B = C, Si, and Ge) binary monolayers
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.