Abstract
We study the sudden quench of a one-dimensional p-wave superconductor through its topological signature in the entanglement spectrum. We show that the long-time evolution of the system and its topological characterization depend on a pseudomagnetic field Reff(k). Furthermore, Reff(k) connects both the initial and the final Hamiltonians, hence exhibiting a memory effect. In particular, we explore the robustness of the Majorana zero-mode and identify the parameter space in which the Majorana zero-mode can revive in the infinite-time limit.
Similar content being viewed by others
Introduction
The implementation of a quantum computer requires fault-tolerant quantum information processing. Conventional quantum error correction codes1 demand an error threshold that is still beyond the reach of the current technology. Alternatively, one may exploit exotic topological excitations that obey non-Abelian braiding statistics to encode quantum information, which would then be robust against local perturbations. Named after Ettore Majorana2, Majorana zero-modes seem to be the easiest to construct among the family of objects that realize non-Abelian statistics. A prototypical model for Majorana zero-modes is the one-dimenaional (1D) p-wave superconductor3, in which different topological phases can be characterized by a topological Z2 index. Topological non-trivial phases can be identified by the presence of zero-energy Majorana edge modes at open boundaries, which may be realized at the interface of superconductors with either topological insulators4,5 or semiconductors with strong spin-orbit coupling6,7,8. Recent experimental progress9 further fuels the interest in the preparation and manipulation of Majorana zero-modes.
To control the Majorana zero-modes for braiding or computing one needs to dynamically change the experimental parameters, such as the gate voltage in a wire network10 or the magnetic flux in a hybrid Majorana-transmon device11. This motivated the study of the out-of-equilibrium dynamics of systems with Majorana modes at the ends12,13,14,15, which found that topology could induce anomalous defect production that could cause quantum decoherence, when a system was adiabatically driven through a quantum critical point. On the other hand, a sudden quench (not necessarily on a topological system) gives rise to the question whether the system can undergo relaxation to an equilibrium state upon a change of parameters. Interestingly, recent studies also showed that the quench dynamics of integrable systems has a memory effect: it reaches a steady state depending strongly on the initial condition16,17,18,19. However, the majority of the studies along that line mostly concern the bulk properties while only few studies also investigate the edge properties20,21,22. In order to use Majorana zero-modes as robust quantum information carriers, it is, hence, of great interest to study the stability of the Majorana edge modes after sudden quenches.
An alternative avenue that connects Majorana zero-modes and quantum information is quantum entanglement. The common entanglement measurement is the von Neumann entropy of a subsystem A: SA = −Tr ρA log2 ρA, where  is the reduced density matrix after tracing out the environment B from the whole system A ∪ B. For a topological system the size-independent constant of the entanglement entropy is related to the total quantum dimension23,24, which can be used to detect topological order. Nevertheless, more information is revealed in the entanglement spectrum, i.e. the eigenvalues of the entanglement Hamiltonian
is the reduced density matrix after tracing out the environment B from the whole system A ∪ B. For a topological system the size-independent constant of the entanglement entropy is related to the total quantum dimension23,24, which can be used to detect topological order. Nevertheless, more information is revealed in the entanglement spectrum, i.e. the eigenvalues of the entanglement Hamiltonian  , whose thermodynamic entropy at “temperature” T = 1 is equivalent to the entanglement entropy25. Under certain circumstances one can view, at least on the low-energy scale, the entanglement Hamiltonian on the subsystem A with the open boundaries as the deformed real-space Hamiltonian that preserves the topological information, hence the presence of zero-energy Majorana edge modes can be detected by a corresponding degeneracy in the entanglement spectrum; more precisely, a pair of doubly degenerate eigenvalues of 1/2 in the one-particle entanglement spectrum26,27,28,29. This provides a reliable measurement of the Majorana edge modes.
, whose thermodynamic entropy at “temperature” T = 1 is equivalent to the entanglement entropy25. Under certain circumstances one can view, at least on the low-energy scale, the entanglement Hamiltonian on the subsystem A with the open boundaries as the deformed real-space Hamiltonian that preserves the topological information, hence the presence of zero-energy Majorana edge modes can be detected by a corresponding degeneracy in the entanglement spectrum; more precisely, a pair of doubly degenerate eigenvalues of 1/2 in the one-particle entanglement spectrum26,27,28,29. This provides a reliable measurement of the Majorana edge modes.
In this report we fuse two subjects by exploring the quench dynamics of Majorana zero-modes of a 1D p-wave superconductor under the entanglement measurement process, thereby offer a quantum information perspective of the manipulation of topological systems and the robustness of the Majorana zero-modes under sudden quench. We find that the topology of the infinite-time behavior can be determined by the properties of a pseudomagnetic field Reff, which connects both the initial and the final Hamiltonians, hence exhibiting a memory effect. In general, a quench across any phase boundary will not give rise to Majorana zero-modes. Surprisingly, the quench within the same topologically nontrivial phase may also lead to the loss of the Majorana modes. We provide an equation describing a critical surface in the parameter space of  ,
,  , and
, and  . For quenches whose parameters lie above the critical surface, the initial Majorana zero-modes can revive in the long-time limit.
. For quenches whose parameters lie above the critical surface, the initial Majorana zero-modes can revive in the long-time limit.
Results
The 1D p-wave superconducting system of spinless fermions proposed by Kitaev3 is described by the Hamiltonian

with the nearest-neighbor hopping amplitude t, superconducting pairing Δ, and on-site chemical potential μ. The translational invariant Hamiltonian (1) can be written as

where σ = (αx, σy, σz) are Pauli matrices, and R(k) = (0, −Δ sin k, t cos k + μ/2) is the pseudomagnetic field. The one-particle energy spectrum is simply  . The spinless p-wave superconductor (1) breaks the time-reversal symmetry but preserves the particle-hole symmetry therefore it belongs to the class D according to the classification of topological insulators and superconductors; it can be characterized by a Z2 topological invariant30,31.
. The spinless p-wave superconductor (1) breaks the time-reversal symmetry but preserves the particle-hole symmetry therefore it belongs to the class D according to the classification of topological insulators and superconductors; it can be characterized by a Z2 topological invariant30,31.
The topological characterization has a simple graphical interpretation26. If the closed loop  of R(k) in the Ry-Rz plane encircles the origin, zero-energy edge states exist and the system is in the nontrivial phase; otherwise, the loop can be continuously deformed to a point with the bulk gap perserved, hence the system is trivial. We plot the phase diagram of the p-wave superconductor in Fig. 1 using dimensionless constants
of R(k) in the Ry-Rz plane encircles the origin, zero-energy edge states exist and the system is in the nontrivial phase; otherwise, the loop can be continuously deformed to a point with the bulk gap perserved, hence the system is trivial. We plot the phase diagram of the p-wave superconductor in Fig. 1 using dimensionless constants  and
and  . For
. For  , there are two different topological nontrivial phases I and II, corresponding to counterclockwise and clockwise windings of R(k) around the origin. Since the winding numbers of R(k) in phase I and II differ by two, these two phases cannot be continuously deformed to one another without closing the bulk gap, so they belong to different phases. Nevertheless, Majorana zero-modes exist at open ends in both phases. On the other hand, the states with
, there are two different topological nontrivial phases I and II, corresponding to counterclockwise and clockwise windings of R(k) around the origin. Since the winding numbers of R(k) in phase I and II differ by two, these two phases cannot be continuously deformed to one another without closing the bulk gap, so they belong to different phases. Nevertheless, Majorana zero-modes exist at open ends in both phases. On the other hand, the states with  are topologically trivial and no Majorana zero-modes exist in phases III and IV.
are topologically trivial and no Majorana zero-modes exist in phases III and IV.
The coordinates are defined as  and
and  . Solid arrow: quench process from (0.5, 2) to (0.5, 1) [to be discussed in Figs 4(a) and 5(b)]. Dashed arrow: quench process from (0.5, 2) to (−0.5, 0.1) [to be discussed in Figs 4(b) and 5(c)]. Insets: Representative traces of R(k) in the Ry-Rz plane. In the topological phases I and II, R(k) encircles the origin (red dots), while in the trivial phases III and IV, R(k) does not encircle the origin.
. Solid arrow: quench process from (0.5, 2) to (0.5, 1) [to be discussed in Figs 4(a) and 5(b)]. Dashed arrow: quench process from (0.5, 2) to (−0.5, 0.1) [to be discussed in Figs 4(b) and 5(c)]. Insets: Representative traces of R(k) in the Ry-Rz plane. In the topological phases I and II, R(k) encircles the origin (red dots), while in the trivial phases III and IV, R(k) does not encircle the origin.
The reduced density matrix ρA can be calculated by the block correlation function matrix (CFM)32,33,34,35,36:  , where λm are the eigenvalues of the block correlation function matrix
, where λm are the eigenvalues of the block correlation function matrix  with
with  and i, j being sites of the finite subsystem A as shown in Fig. 2. λm is known as the one-particle entanglement spectum (OPES). For total system AB the bulk correlation function matrix is a 2 × 2 matrix in the Fourier space27. Specifically for the Hamiltonian (2) one has
and i, j being sites of the finite subsystem A as shown in Fig. 2. λm is known as the one-particle entanglement spectum (OPES). For total system AB the bulk correlation function matrix is a 2 × 2 matrix in the Fourier space27. Specifically for the Hamiltonian (2) one has

where k ∈ (−π, π]. To connect the CFM and the edge state recall that in one dimension the nontrivial Berry phase for the periodic systems in their thermodynamic limit confirms the topological nature of the systems. According to the bulk-edge correspondence37, two edge states with zero energy appear for the far-apart open boundaries. The same story can also happen with the entanglement spectra. The entanglement Hamiltonian Hent defined as  is related to the block correlation function matrix C in the following way34,35:
is related to the block correlation function matrix C in the following way34,35:

where i, j ∈ A. Therefore the entanglement Hamiltonian shares the same eigenvalues of the block correlation function matrix C. From the discussion above we know that the Berry phase of C in its thermodynamic limit is also determined by the pseud-magnetic field R. According the bulk-edge correspondence we conclude that there appear two edge states for the block correlation function matrix C due to the natural open boundaries of the block and therefore the entanglement spectra share the same edge states.
On the other hand, by comparing H(k) (Eq. 2) and C(k) (Eq. 3) it is evident that they have the same topological characterization. By applying the bulk-edge correspondence to both the original and entanglement Hamiltonian one see that the zero energy edge modes of the original Hamiltonian correspond to the λm = 1/2 eigenvalues of the correlation function matrix. Therefore, in the topological phases I and II, the signature of Majorana zero-modes is the degenerate eigenvalues λm = 1/2 in the OPES.
The Majorana zero-modes play an important role in the entanglement between the subsystem A with its environment B. We can calculate the entanglement entropy ES for the partition as  where Sm = −λm log2 λm − (1 − λm) log2(1 − λm). The pair of Majorana modes with λm = 1/2 contribute the maximal entanglement Sm = 1. Hence they are known as the topological maximally-entangled states (tMES)28,29.
where Sm = −λm log2 λm − (1 − λm) log2(1 − λm). The pair of Majorana modes with λm = 1/2 contribute the maximal entanglement Sm = 1. Hence they are known as the topological maximally-entangled states (tMES)28,29.
Different from non-integrable models, which will be thermalized at infinite time, the quench dynamics of integrable models has become an important topic since such a bulk system will not be thermalized but reach a steady state decided by the initial condition described by general Gibbs ensemble (GGE). On the other hand, the Majorana edge modes are tMES, robust against perturbations, it is interesting to question how a sudden quench affect the Majorana zero-modes. Naively, if we quench from a topological phase to a trivial one, the Majorana modes may evolve into the bulk, mix with bulk modes, and disappear eventually. What happens, then, if we quench from a trivial phase to a topological one, or from a topological phase to a different one? Will the static information in the final Hamiltonian dictate the dynamical state in the long-time limit?
To answer these questions we perform a sudden quench to the p-wave superconductor at t = 0 by switching Δ and μ at t < 0 to Δ′ and μ′ at t > 0. This changes the Hamiltonian from H to H′ and, correspondingly, R to R′. We then calculate the time-dependent OPES λm(t) by diagonalizing the time-dependent CFM  for i, j ∈ A. We first consider the quench processes across phase boundaries and focus on λm close to 1/2 as we are primarily interested in the fate of the Majorana zero-modes.
for i, j ∈ A. We first consider the quench processes across phase boundaries and focus on λm close to 1/2 as we are primarily interested in the fate of the Majorana zero-modes.
Figure 3(a–c) show the time evolution of the OPES near 1/2 by suddenly quenching the systems from phases II, III, and IV, respectively, to phase I. We find that the Majorana zero-modes fail to appear after a sufficiently long time, regardless of the topological properties of the original state. In other words, the quench of the topological systems with the Majorana edge modes cannot be thermalized. For comparison, Fig. 3(d–f) show the time evolution of the OPES for the sudden quench from phase I to phases II, III, and IV, respectively. The degenerate eigenvalues λm = 1/2 persist for some time before they split and relax to separate values, depending on the final Hamiltonian. In other words, the Majorana zero-modes before a sudden quench are destroyed eventually.
Representative time evolutions of the OPES close to 1/2 for quenches between (a) II-I, (b) III-I, (c) IV-I, (d) I-II, (e) I-III, and (f) I-IV. The initial or final parameters ( ,
,  ) are (0.5, 2) for phase I, (0.5, −2) for phase II, (2, 2) for phase III, and (−2, 2) for phase IV. The size of the subsystem A is L = 100. Insets: The corresponding curves of Reff(k) in the Ry-Rz plane. The absence of the tMES in the long-time limit is reflected by the passing of Reff(k) at the origin.
) are (0.5, 2) for phase I, (0.5, −2) for phase II, (2, 2) for phase III, and (−2, 2) for phase IV. The size of the subsystem A is L = 100. Insets: The corresponding curves of Reff(k) in the Ry-Rz plane. The absence of the tMES in the long-time limit is reflected by the passing of Reff(k) at the origin.
To further confirm the topology of the steady states of the quench process in the infinite-time limit, we analyse the time-dependent CFM in Fourier space G(k, t) as illustrated in the method section: Time-dependent correlation matrix. We find it can be described by a pseudomagnetic field R(k, t) (15) through the relation G(k, t) = [1 − R(k, t) · σ]/2. In the infinite-time limit the sinusoidal time dependence dephases away and G(k, t = ∞) depends only on the effective pseudomagnetic field

Therefore, the topology of the steady state is determined by both the initial and final Hamiltonians: the quench dynamics has a memory of the initial Hamiltonian, albeit entangled with the final Hamiltonian. The insets in Fig. 3 dipict Reff(k) in the above cases. We confirm that all the traces pass through the origin, indicating that the Majorana zero-modes are not stable in the infinite-time limit.
Will Majorana zero-modes persist if we quench between two Hamiltonians in the same topological phase? Given the fact that the edge states cannot thermalize, the naive answer of yes needs to be examined. In Fig. 4(a,b) we show the OPES evolution near 1/2 for two quantum quenches both within phase I, as indicated in the phase diagram in Fig. 1. Surprisingly, we find that the Majorana zero-modes reappear in the steady state in the infinite-time limit in Fig. 4(a), while disappear in Fig. 4(b). This contrasts to the persistence of the edge modes in a dimerized chain, where the edge mode is an electron instead of Majorana zero-modes29. We also plot the corresponding Reff(k) in the insets of Fig. 4(a,b). Reff(k) encircles the origin in the former case, which confirms the persistent memory of the Majorana modes after a sudden quench. In sharp contrast, Reff(k) passes through the origin in the latter case, which is consistent with the loss of the memory of the Majorana modes. Note that the quench processes within the phase II shall behave similarly.
The time evolution of the OPES near 1/2 for two sudden quenches [marked by (a) solid arrow ((0.5, 2) to (0.5, 1)) and (b) dashed arrow ((0.5, 2) to (−0.5, 0.1)) in Fig. 1] within phase I. The tMES are recovered eventually in (a), but not in (b). Insets in (a,b): Traces of Reff(k) in the Ry-Rz plane. The size of subsystem A is L = 100.
To support our findings, we further analyze the eigenstates of the after a sudden quench. In Fig. 5 we plot the probability sum  of the two states ψ1,2 whose eigenvalues are closest to 1/2 at t = 0, 9, and 99. As expected, Psum exhibits sharp peaks due to the presence of the Majorana edge modes. The only case that such peaks survive [Fig. 5(b)] is the quench process within phase I as discussed in Fig. 4(a). For comparison, such peaks dissolve into the bulk when we quenches the system to a different topological phase [Fig. 5(a)] or within phase I but with mismatching superconducting gaps [Fig. 5(c)].
of the two states ψ1,2 whose eigenvalues are closest to 1/2 at t = 0, 9, and 99. As expected, Psum exhibits sharp peaks due to the presence of the Majorana edge modes. The only case that such peaks survive [Fig. 5(b)] is the quench process within phase I as discussed in Fig. 4(a). For comparison, such peaks dissolve into the bulk when we quenches the system to a different topological phase [Fig. 5(a)] or within phase I but with mismatching superconducting gaps [Fig. 5(c)].
Discussion
We have shown in the result section that the maximally entangled states (or Majarona zero modes) can still disappear at t → ∞ even for the quench between the same topological phase. As hinted from (5), this is due to the condition  happens at some k. Explicitly, this means
happens at some k. Explicitly, this means

where  and
and  . Figure 6(a) shows the critical surface below which the equality can be satisfied for some k; while above the surface Reff(k) encircles the origin (to ensure that both the initial and final Hamiltonians are in the topological phase, we also need
. Figure 6(a) shows the critical surface below which the equality can be satisfied for some k; while above the surface Reff(k) encircles the origin (to ensure that both the initial and final Hamiltonians are in the topological phase, we also need 
 ), hence the Majorana zero-modes are memorized in the long-time limit. To understand why
), hence the Majorana zero-modes are memorized in the long-time limit. To understand why  can vanish at some k, we find it is instructive to consider the velocity of the R-vectors. Intuitively, if the velocity profiles of two R-vectors are similar then it is impossible to have
can vanish at some k, we find it is instructive to consider the velocity of the R-vectors. Intuitively, if the velocity profiles of two R-vectors are similar then it is impossible to have  . In contrast, if the maximal angular velocity of R(k) and R′(k) occur at different k points then it is possible to have
. In contrast, if the maximal angular velocity of R(k) and R′(k) occur at different k points then it is possible to have  . For example, if R(k) rotates rapidly while R′(k) rotates slowly then they should become perpendicular at some k. As shown in the method section: Maximal angular velocity and band gap, we find the position of the band gap and the maximal of the angular speed ω(k) = dR(k)/dk are at the same k (can be slightly different for some special parameter region). Since the position of the band gap can be tuned by the chemical potential μ, one can make the maximal angular velocity of R(k) and R′(k) occur at different k by tuning the chemical potential of the initial and final Hamiltonian. Thus, for the quench within the same topologically non-trivial phases (both R and R′ vectors rotate clockwise or counter-clockwise), it is still possible to make R rotates slowly (rapidly) while R′ rotates rapidly (slowly) at a particular k, leading to
. For example, if R(k) rotates rapidly while R′(k) rotates slowly then they should become perpendicular at some k. As shown in the method section: Maximal angular velocity and band gap, we find the position of the band gap and the maximal of the angular speed ω(k) = dR(k)/dk are at the same k (can be slightly different for some special parameter region). Since the position of the band gap can be tuned by the chemical potential μ, one can make the maximal angular velocity of R(k) and R′(k) occur at different k by tuning the chemical potential of the initial and final Hamiltonian. Thus, for the quench within the same topologically non-trivial phases (both R and R′ vectors rotate clockwise or counter-clockwise), it is still possible to make R rotates slowly (rapidly) while R′ rotates rapidly (slowly) at a particular k, leading to  . A simple physical picture to understand this phenomenon is as follows: if the superconducting gaps of the initial and final Hamiltonians have no energy overlap, the Majorana modes are suppressed due to the mismatch of the corresponding single-particle states.
. A simple physical picture to understand this phenomenon is as follows: if the superconducting gaps of the initial and final Hamiltonians have no energy overlap, the Majorana modes are suppressed due to the mismatch of the corresponding single-particle states.
For the early time behavior, one may ask what determines the finite survival time of the degenerate λm = 1/2 in Fig. 3(d–f). We can imagine that upon quench quasiparticles are generate in the bulk and propagate at a maximum velocity vmax = [∂ε(k)/∂k]max. Therefore, at  the Majorana zero-modes at the boundaries of the entanglement cut can exchange information and hence the degenerate levels in the OPES start to split. Chaotic oscillations then emerge in the entanglement spectrum due to the complex processes of quasiparticle interference and decoherence.
the Majorana zero-modes at the boundaries of the entanglement cut can exchange information and hence the degenerate levels in the OPES start to split. Chaotic oscillations then emerge in the entanglement spectrum due to the complex processes of quasiparticle interference and decoherence.
Finally, we discuss the robustness of our result under the perturbative Coulomb interactions:  for the final Hamiltonian. Within the mean-field approach, the effects of the interaction is to renormalize the hopping, paring and chemical potential, resulting an effective mean-field Hamiltonian of the form of the un-perturbed Hamiltonian. As a result, the renormalized hopping
for the final Hamiltonian. Within the mean-field approach, the effects of the interaction is to renormalize the hopping, paring and chemical potential, resulting an effective mean-field Hamiltonian of the form of the un-perturbed Hamiltonian. As a result, the renormalized hopping  , paring
, paring  and chemical potential
and chemical potential  of
of  are given by the self-consistent equations (7)
are given by the self-consistent equations (7)

where  are the pseudomagnetic fields of
are the pseudomagnetic fields of  with the form given by (2). To understand the effect of the mean-field approach, the same example as Fig. 4(a) (same as Fig. 5(b)) is considered in the follow calculation. Considering V = 0.1 for the final Hamiltonian, we obtain
with the form given by (2). To understand the effect of the mean-field approach, the same example as Fig. 4(a) (same as Fig. 5(b)) is considered in the follow calculation. Considering V = 0.1 for the final Hamiltonian, we obtain  and
and  corresponding to the movement from the initial black point to the red one in Fig. 7. However this change under perturbation does not cross the critical surface which is plotted as the blue curve in Fig. 7. The results are confirmed by Fig. 8, where the two OPES ψ1 and ψ2 near 1/2 and the probability sum
corresponding to the movement from the initial black point to the red one in Fig. 7. However this change under perturbation does not cross the critical surface which is plotted as the blue curve in Fig. 7. The results are confirmed by Fig. 8, where the two OPES ψ1 and ψ2 near 1/2 and the probability sum  at t = 0, 9, and 99 for the red point are shown. As far as the final Hamiltonian is far away from the critical surface, the perturbations of the interaction do not affect the revival of the tMES. The same considerations also apply for the perturbation of the pairing and chemical potential.
at t = 0, 9, and 99 for the red point are shown. As far as the final Hamiltonian is far away from the critical surface, the perturbations of the interaction do not affect the revival of the tMES. The same considerations also apply for the perturbation of the pairing and chemical potential.
 with fixed
with fixed  .
.In summary, we study the quench dynamics of a 1D p-wave superconductor using the OPES. We find that the system reach a final steady state whose topology can be determined by an effective pseudomagnetic field Reff(k) (5). As expected, sudden quenches from a topological phase to a trivial phase destroy the Majorana edge modes. However, the memory of the Majorana modes will also be lost if we quench the system to a different topological phase, or if the superconducting gaps before and after a sudden quench do not match. When both topological and energetic criteria are satisfied, the Majorana zero-modes will return after sufficiently long time.
Methods
Time-dependent correlation function
To obtain the time-dependent correlation function matrix  , one has to diagonalize H (2) using
, one has to diagonalize H (2) using

where

Therefore, the diagonal basis  is defined as
is defined as

where  . Assume the notation with and without ′ using the parameter set (t, μ, Δ) before and (t′, μ′, Δ′) after a sudden quench respectively, the time-dependent CFM after a sudden quench in the Fourier space
. Assume the notation with and without ′ using the parameter set (t, μ, Δ) before and (t′, μ′, Δ′) after a sudden quench respectively, the time-dependent CFM after a sudden quench in the Fourier space

can be calculated by canonically transforming  twice to the proper operators using (9) and obtain
twice to the proper operators using (9) and obtain

For zero temperature, ρ is the density matrix of the ground state, therefore

Substituting (13) and (9) into (12) and using the properties of Pauli matrices (R · σ) (R′ · σ) = R · R′ + i(R × R′) · σ, we end up with a simple form

where the effective pseudomagnetic field

where  and
and  .
.
Maximal angular velocity and band gap
Here we are going to determine the momentum k0 at which ω(k) reaches global maxima and the momentum kg at which the band gap of the dispersion ε(k) is located. Then, we illustrate an interesting relation between angular velocity ω(k) and the dispersion ε(k): that one has k0 = kg in some parameter regimes and k0 ≈ kg in other parameter regimes as shown in Fig. 9. This provides an intuitive picture on why the topology of the steady state is determined by the initial and final Hamiltonian as discussed in the discussion section.
In the following, we will use the dimensionless parameters  ,
,  and set t = 1 as our unit of energy. Furthermore, we will assume that
and set t = 1 as our unit of energy. Furthermore, we will assume that  since we only want to consider the region of topologically non-trivial phases.
since we only want to consider the region of topologically non-trivial phases.
Extrema of the angular velocity ω(k)
To identify the momentum k0 at which the angular velocity ω(k) reaches its maximum, we start from the pseudomagnetic field

In terms of the dimensionless constants defined above it can be rewrite as

where  , and
, and  . This shows that R(k) can be decomposed into as constant vector in the z-direction, and rotating and counter-rotating vectors in the y-z-plane. Let θ(k) be the angle between R(k) and the z-axis, then one has
. This shows that R(k) can be decomposed into as constant vector in the z-direction, and rotating and counter-rotating vectors in the y-z-plane. Let θ(k) be the angle between R(k) and the z-axis, then one has

Define the angular velocity as ω(k) = dθ(k)/dk. By differentiating the equation above we obtain the expression of angular velocity

The k0 at which the angular velocity ω(k) reaches its maximum should satisfy  . It is straightforward to show that
. It is straightforward to show that

where

and ε(k) is the dispersion. We note that due to the finite band gap, the denominator is always non-zero. From Eq. (20) we find k0 = 0 or k = π or

provided that

Note that in Eq. (22) we have discarded the solution with positive sign in front of the square root because it does not lead to a valid solution.
Extrema of the dispersion ε(k)
To identify the momentum kg at which the band gap is located we start from the dispersion

The kg should satisfy  , where
, where

This leads to

Solving for kg we find kg = 0 or kg = π or

provided that

Relationship between k0 and kg
With the solution of k0, the location of the maximal angular velocity ω(k) and kg the location of the gap of the dispersion ε(k) we are now is position to illustrate the close relation between k0 and kg. In Fig. 9 we show the difference |k0 − kg| as a function of  and
and  . We find that k0 and kg are almost the same in most of the parameter regime. In the following we provide more insight on why this happens via analyzing the solutions in various limits.
. We find that k0 and kg are almost the same in most of the parameter regime. In the following we provide more insight on why this happens via analyzing the solutions in various limits.
• Case 1: ko = kg = 0 or π
Consider first the case where both Eqs (22) and (27) do not lead to a valid solution. In this case one has k0 = 0 or k0 = π and similarly for the kg. Since

and

one finds that if  then k0 = kg = 0, while if
then k0 = kg = 0, while if  then k0 = kg = π. Therefore the location of the band gap and the maximum angular velocity are at the same k, as shown in Fig. 10(a,b) for
then k0 = kg = π. Therefore the location of the band gap and the maximum angular velocity are at the same k, as shown in Fig. 10(a,b) for  and
and  respectively.
respectively.
• Case 2: Strong paring; 
Consider next the case of strong pairing, where  . Due to the restriction of
. Due to the restriction of  it is straightforward to show that in this case the square root of Eq. (22) is always positive. It is then instructive to consider the two limits of
it is straightforward to show that in this case the square root of Eq. (22) is always positive. It is then instructive to consider the two limits of  :
:  and
and  .In limit of
.In limit of  , one has
, one has

and

Consequently both Eqs (22) and (27) have no valid solution and one falls back to the scenario of case 1.
In the other limit of  , Eq. (22) becomes
, Eq. (22) becomes

while the Eq. (27) becomes

In Fig. 11 we plot the absolute value of Eq. (33) as a function of  and show that there is always a solution for k0 within the parameter regime. Due to the
and show that there is always a solution for k0 within the parameter regime. Due to the  dependence of k0, in this limit one has k0 ≠ kg. However, in this limit one also finds
dependence of k0, in this limit one has k0 ≠ kg. However, in this limit one also finds
 .
.

By comparing Eqs (29) and (35), one finds that in this limit Eq. (33) defines a minimum of the angular speed instead of a maximum. Similarly, by comparing Eqs (30) and (36) one finds that the band gap is not located at the momentum defined by Eq. (34). Therefore, we again go back to the scenario of case 1 as shown in Fig. 10(c).
• Case 3: Week paring; 
Consider finally the case of weak pairing, where  . In this case, the term in the square root of Eq. (22) may become negative when
. In this case, the term in the square root of Eq. (22) may become negative when  and gives no valid solution for k0. However, the same condition also leads to
and gives no valid solution for k0. However, the same condition also leads to

which means there is also no valid solution for kg according to Eq. (27). Consequently one again falls back to the scenario of case 1.
In order to have a valid solution one requires  , which means
, which means  . It is then instructive to consider the limits of
. It is then instructive to consider the limits of  and
and  . Consider first the limit of
. Consider first the limit of  where Eqs (22) and (27) become
where Eqs (22) and (27) become

This means that the k0 and kg are asymptotically close to each other when the paring goes to zero. On the other hand, in this limit we also have


By comparing Eqs (29) and (39), one finds Eq. (39) indeed defines the maximum of the angular velocity. Similarly, Eq. (40) defines the band gap, which can be easily verified by comparing Eqs (30) and (40). Thus, the k0 and kg defined in Eqs (22) and (27) are almost the same as shown in Fig. 10(d).
On the other hand, for limit of  , Eqs (22) and (27) become
, Eqs (22) and (27) become

which gives no valid solution for k0 and kg due to the restriction of  and thus falls back to scenario of case 1.
and thus falls back to scenario of case 1.
Additional Information
How to cite this article: Chung, M.-C. et al. A Memory of Majorana Modes through Quantum Quench. Sci. Rep. 6, 29172; doi: 10.1038/srep29172 (2016).
References
Shor, P. W. Fault-tolerant quantum computation. Proceedings of the 37th Symposium on the Foundations of Computer Science, 56 (1996).
Majorana, E. A symmetric theory of electrons and positrons. Nuovo Cimento 14, 171 (1937).
Kitaev, A. Unpaired Majorana fermions in quantum wires. Phys.-Usp. 44, 131 (2001).
Fu, L. & Kane, C. L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 100, 096407 (2008).
Fu, L. & Kane, C. L. Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction. Phys. Rev. B 79, 161408(R) (2009).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Sau, J. D. et al. Generic New Platform for Topological Quantum Computation Using Semiconductor Heterostructures. Phys. Rev. Lett. 104, 040502 (2010).
Oreg, Y., Refael, G. & von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 105, 177002 (2010).
Mourik, V. et al. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science 336, 1003 (2012).
Alicea, J. et al. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nature Phys. 7, 412 (2011).
Hyart, T. et al. Flux-controlled quantum computation with Majorana fermions. Phys. Rev. B 88, 035121 (2013).
Bermudez, A. et al. Topology-Induced Anomalous Defect Production by Crossing a Quantum Critical Point. Phys. Rev. Lett. 102, 135702 (2009).
Bermudez, A., Amico, L. & Martin-Delgado, M. A. Dynamical delocalization of Majorana edge states by sweeping across a quantum critical point. New J. Phys. 12, 055014 (2010).
DeGottardi, W., Sen, D. & Vishveshwara, S. Topological phases, Majorana modes and quench dynamics in a spin ladder system. New J. Phys. 13, 065028 (2011).
Hegde, S. et al. Quench dynamics and parity blocking in Majorana wires. New J. Phys. 17, 053036 (2015).
Rigol, M. et al. Relaxation in a Completely Integrable Many-Body Quantum System: An Ab Initio Study of the Dynamics of the Highly Excited States of 1D Lattice Hard-Core Bosons. Phys. Rev. Lett. 98, 050405 (2007).
Rigol, M., Muramatsu, A. & Olanshii, M. Hard-core bosons on optical superlattices: Dynamics and relaxation in the superfluid and insulating regimes. Phys. Rev. A 74, 053616 (2006).
Cazalilla, M. A., Iucci, A. & Chung, M.-C. Thermalization and quantum correlations in exactly solvable models. Phys. Rev. E 85, 011133 (2012).
Chung, M.-C., Iucci, A. & Cazalilla, M. A. Thermalization in systems with bipartite eigenmode entanglement. New J. Phys. 14, 075013 (2012).
Patel, A. A., Sharma, S. & Dutta, A. Quench dynamics of edge states in 2-d topological insulator ribbons. Eur. Phys. J. B 86, 367 (2013).
Rajak, A. & Dutta, A. Survival probability of an edge Majorana in a one-dimensional p-wave superconducting chain under sudden quenching of parameters. Phys. Rev. E 89, 042125 (2014).
Vasseur, R., Dahlhaus, J. P. & Moore, J. E. Universal Nonequilibrium Signatures of Majorana Zero Modes in Quench Dynamics. Phys. Rev. X 4, 041007 (2014).
Kitaev, A. & Preskill, J. Topological Entanglement Entropy. Phys. Rev. Lett. 96, 110404 (2006).
Levin, M. & Wen, X.-G. Detecting Topological Order in a Ground State Wave Function. Phys. Rev. Lett. 96, 110405 (2006).
Li, H. & Haldane, F. D. M. Entanglement Spectrum as a Generalization of Entanglement Entropy: Identification of Topological Order in Non-Abelian Fractional Quantum Hall Effect States. Phys. Rev. Lett. 101, 010504 (2008).
Ryu, S. & Hatsugai, Y. Topological Origin of Zero-Energy Edge States in Particle-Hole Symmetric Systems. Phys. Rev. Lett. 89, 077002 (2002).
Ryu, S. & Hatsugai, Y. Entanglement entropy and the Berry phase in the solid state. Phys. Rev. B 73, 245115 (2006).
Chung, M.-C. et al. Edge states, entanglement entropy spectra and critical hopping couplings of anisotropic honeycomb lattices. Eur. Phys. Lett. 95, 27003 (2011).
Chung, M.-C. et al. Quench dynamics of topological maximally entangled states. J. Phys. Condens. Matter 25, 285601 (2013).
Schnyder, A. P. et al. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Fidkowski, L. & Kitaev, A. Effects of interactions on the topological classification of free fermion systems. Phys. Rev. B 81, 134509 (2010).
For a review, see Peschel, I. & Eisler, V. Reduced density matrices and entanglement entropy in free lattice models, J. Phys. A: Math. Theor. 42, 504003 (2009).
Chung, M.-C. & Peschel, I. Density-matrix spectra of solvable fermionic systems. Phys. Rev. B 64, 064412 (2001).
Peschel, I. Calculation of reduced density matrices from correlation functions. J. Phys. A 36, L205 (2003).
Cheong, S. A. & Henley, C. L. Many-body density matrices for free fermions. Phys. Rev. B 69, 075111 (2004).
Barthel, T., Chung, M.-C. & Schollwöck, U. Entanglement scaling in critical two-dimensional fermionic and bosonic systems. Phys. Rev. A 74, 022329 (2006).
Bernevig, B. A. & Hughes, T. L. Topological Insulators and Topological Superconductors (Princeton University Press, Princeton, NJ, 2013).
Acknowledgements
M.-C.C., P.C. and C.-Y.M. acknowledge the NSC support under the contract Nos 102-2112-M-005-001-MY3, 101-2112-M-007-010, and 100-2112-M-007-011-MY3, respectively. X.W. acknowledges the support by the 973 Program under Project No. 2012CB927404 and the NSFC Project No. 11174246.
Author information
Authors and Affiliations
Contributions
M.-C.C. coordinated this project. M.-C.C. provided the theoretical frame work. Y.-H.J. finished the numerical calculations and figures. P.C. and Y.-H.J. wrote the method part of this report and M.-C.C. wrote the main part (the rest) of this report. X.W. and C.-Y.M. contributed the physical understanding of the phase diagram of the steady state. All authors participated in the discussions for this report.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chung, MC., Jhu, YH., Chen, P. et al. A Memory of Majorana Modes through Quantum Quench. Sci Rep 6, 29172 (2016). https://doi.org/10.1038/srep29172
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep29172
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

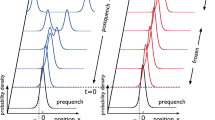






 of the two eigenstates of the entanglement Hamiltonian whose eigenvalues are closest to 1/2 at t = 0, 9, and 99 after a sudden quench (a) from I (0.5, 2) to II (0.5, −2), (b) from I (0.5, 2) to I (0.5, 1) as in
of the two eigenstates of the entanglement Hamiltonian whose eigenvalues are closest to 1/2 at t = 0, 9, and 99 after a sudden quench (a) from I (0.5, 2) to II (0.5, −2), (b) from I (0.5, 2) to I (0.5, 1) as in 
 ,
,  , and
, and  above which Reff(k) = 0 has no solution. (b) Cross sections of the critical surface at
above which Reff(k) = 0 has no solution. (b) Cross sections of the critical surface at  , 0, and 0.4.
, 0, and 0.4.
 using V = 0.1 are shown as the red point.
using V = 0.1 are shown as the red point.
 at time t = 0, 9 and 99 for the perturbation.
at time t = 0, 9 and 99 for the perturbation.

 and
and  ). (b) Case 1 with band gap locates at 0 (
). (b) Case 1 with band gap locates at 0 ( and
and  ). (c) The situation belongs to limit
). (c) The situation belongs to limit  of case 2 (
of case 2 ( and
and  ). (d) The situation belongs to limit
). (d) The situation belongs to limit  of case 3 (
of case 3 ( and
and  ).
).