Introduction

Gauge theories play a pivotal role in providing a unified description of standard model in particle physics. In recent decades, gauge theories have also found applicability in condensed matter physics1,2, particularly in the context of the many-body systems, leading to the emergence of lattice gauge theories3. Prominent examples include the lattice gauge descriptions of quantum magnets4, high-Tc superconductors5 and quantum simulation6,7,8,9,10,11,12,13,14,15,16,17. The local gauge symmetry inherent in these theories gives rise to a multitude of conserved quantities, making them a valuable platform for investigating the localization phenomena in the absence of disorder18,19,20,21,22,23,24. The lattice gauge theory framework holds great promise for the development of specialized digital and analogue quantum simulators, with the ultimate goal of realizing universal quantum computers. Consequently, this field has garnered significant attention in experimental research. Currently, the realization of \({{\mathbb{Z}}}_{2}\) lattice gauge theory has been successfully achieved using diverse quantum resources such as ultracold atoms8,14, superconducting circuits15, and Rydberg atomic arrays16. These experiments hold profound significance in guiding the study of disorder-free localization.

Recently, the non-Hermitian physics has attached widespread attention due to the discovery of numerous physical properties that transcend those exhibited by the Hermitian systems25,26,27. For instance, the non-Hermitian skin effect has unveiled the sensitivity to the spatial boundary conditions28,29,30, the non-Hermiticity has expanded the realm of topological phases beyond the Hermitian framework29,30,31, the interplay of non-Hermiticity and disorder has given rise to the emergence of the localization-delocalization transitions32,33,34,35. Non-Hermitian physics finds wide-ranging applicability across various physical systems, including optics36, acoustics37, cold atoms38,39, etc. Therefore, conducting in-depth investigations and achieving precise control over non-Hermitian properties can provide a solid foundation for the practical implementation of non-Hermitian physics in diverse systems.

Localization behaviors have been extensively investigated in the non-Hermitian systems with nonreciprocal hopping32,33,40,41,42, gain or loss32,43 and quasiperiodic lattices33,44,45. However, much less is known about the interplay of the non-Hermiticity and lattice gauge field. Motivated by recent developments, the present study focus on the non-Hermitian extension of 1D lattice model of spinless fermions coupled through spins 1/2, as illustrated in Fig. 1. The spin subsystem in this model act as a \({{\mathbb{Z}}}_{2}\) gauge field for the fermions. The nonreciprocal hopping introduces non-Hermiticity, thereby prompting us to investigate the nonequilibrium dynamics of systems subjected to the influence of a \({{\mathbb{Z}}}_{2}\) gauge field and non-Hermiticity.

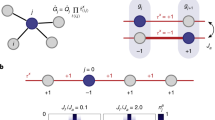
Fig. 1: Schematic representation of the non-Hermitian system.
figure 1

Spinless fermions (blue circles) with nonreciprocal hopping (left-hopping amplitude Jeg and right-hopping amplitude Je−g) are coupled via the spins S = 1/2 living on the bonds (orange bonds). Dual spins \(\hat{\tau }\) (red arrows) are shown in the configuration corresponding to the \(\hat{\sigma }\) spins (orange arrows).

Full size image

Through duality mapping19,46,47, we investigate the quench dynamics of fermions in an effective binary disorder potential. We show that the disorder-free localization-delocalization transition arises from the interplay between the non-Hermitian skin effects and the \({{\mathbb{Z}}}_{2}\) gauge field. This phase transition is closely associated with the real-complex transition of eigenenergies. Moreover, in the dynamics of quantum mutual information of fermions and spins, two distinct scaling laws are observed in both the localized and delocalized phases, which are the fingerprints of the non-Hermitian quantum disentangled liquids. In the localized phase, the \({{\mathbb{Z}}}_{2}\) gauge field dominates the area law scaling, while the non-Hermitian skin effect results in the area law scaling in the delocalized phase. Furthermore, we demonstrate that the non-Hermiticity induces the flow of quantum information from the fermions to the spins. Our result not only opens a way for preparing and controlling the quantum correlated states in the nonequilibrium systems, but also provides insights into the quantum simulation of lattice gauge theory.

Results

Model

We consider the 1D lattice model of spinless fermions with the nonreciprocal hopping, where the fermions are coupled through the bond spins characterized by S = 1/2, see Fig. 1. The Hamiltonian governing this system is given by

$$\hat{H} = - J\mathop{\sum}\limits_{j}{\hat{\sigma }}_{j,j+1}^{z}\left({{{{{{{{\rm{e}}}}}}}}}^{g}{\hat{f}}_{j}^{{{{\dagger}}} }{\hat{f}}_{j+1}+{{{{{{{{\rm{e}}}}}}}}}^{-g}{{{{{{{\rm{H.c.}}}}}}}}\right)\\ - h\mathop{\sum}\limits_{j}{\hat{\sigma }}_{j-1,j}^{x}{\hat{\sigma }}_{j,j+1}^{x}$$
(1)

where J and h are the fermion tunneling strength and Ising coupling, respectively. Jeg (Je−g) is the left (right)-hopping amplitude introducing the non-Hermiticity which could be realized in synthetic matter using, for example, photonic systems48,49, topolectrical circuits50, or ultracold atom systems38,51. In the following, we will set J = 1 as the units of energy and choose a fixed fermion number Nf = L/2 (half-filling), where L is the number of sites. This system is invariant under the \({{\mathbb{Z}}}_{2}\) gauge transformation

$${\hat{f}}_{i}\to {\gamma }_{i}{\hat{f}}_{i},\quad {\hat{f}}_{i}^{{{{\dagger}}} }\to {\gamma }_{i}{\hat{f}}_{i}^{{{{\dagger}}} },\quad {\hat{\sigma }}_{j,j+1}^{z}\to {\gamma }_{i}{\hat{\sigma }}_{j,j+1}^{z}{\gamma }_{i+1},$$
(2)

where γi = ± 1 is a local gauge function. The generator of the \({{\mathbb{Z}}}_{2}\) gauge transformation is given by the unitary operator

$$G=\mathop{\prod}\limits_{i}{G}_{i}^{(1-{\gamma }_{i})/2},$$
(3)

where \({G}_{i}={(-1)}^{{\hat{n}}_{i}}{\hat{\sigma }}_{i-1,i}^{z}{\hat{\sigma }}_{i,i+1}^{z}\), and \({\hat{n}}_{i}={\hat{f}}_{i}^{{{{\dagger}}} }{\hat{f}}_{i}\) is the local number operator of fermions. It is note that \({G}_{i}^{2}=1\) and \([{G}_{i},{G}_{j}]=0\) for all i, j. Therefore, the Hamiltonian is gauge invariant, i.e., \([G,H]=0\) for all choices of gauge function γi.

In order to explore the dynamics of fermions, an extensive number of conserved charges can be identified by a duality mapping (see Methods). Then an effective Hamiltonian with fermion operator \({\hat{C}}_{j}={\hat{\tau }}_{j}{\hat{f}}_{j}\) is written as

$${\hat{H}}_{\left\{{q}_{i}\right\}} = - J\mathop{\sum}\limits_{i}({{{{{{{{\rm{e}}}}}}}}}^{g}{\hat{C}}_{i}^{{{{\dagger}}} }{\hat{C}}_{i+1}+{{{{{{{{\rm{e}}}}}}}}}^{-g}{\hat{C}}_{i+1}^{{{{\dagger}}} }{\hat{C}}_{i})\\ +2h\mathop{\sum}\limits_{i}{\hat{q}}_{i}({\hat{C}}_{i}^{{{{\dagger}}} }{\hat{C}}_{i}-1/2),$$
(4)

which describes a nonreciprocal hopping tight-binding model with the binary disorder potential dominated by the charge sectors \(\{{q}_{j}\}\).

We choose the tensor products of fermion and spin states \(\left\vert {{{\Psi }}}_{0}\right\rangle ={\left\vert S\right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}\otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{f}}}}}}}}}\) as the initial state that can be transformed to the one in the Hilbert space of the \(\hat{C}\) degrees of freedom,

$$\left\vert {{{\Psi }}}_{0}\right\rangle = {\left\vert \uparrow \uparrow \uparrow \cdots \right\rangle }_{\sigma }\otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{C}}}}}}}}}\\ =\frac{1}{\sqrt{{2}^{N-1}}}\mathop{\sum}\limits_{\{{q}_{i}\}=\pm 1}\left\vert {q}_{1},{q}_{2},\cdots \,,{q}_{N}\right\rangle \otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{C}}}}}}}}},$$
(5)

where the spin states are restricted to the z-polarized state \({\left\vert S\right\rangle }_{\sigma }=\left\vert \uparrow \uparrow \uparrow \cdots \,\right\rangle\), and the sum is over all possible charge configurations \(\left\{{q}_{i}\right\}=\pm 1\). The quench dynamics of whole system is governed by

$$\left\vert {{\Psi }}(t)\right\rangle =\frac{{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}\hat{H}t}\left\vert {{{\Psi }}}_{0}\right\rangle }{\parallel {{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}\hat{H}t}\left\vert {{{\Psi }}}_{0}\right\rangle \parallel },$$
(6)

where the normalization takes into account the fact that the norm is not conserved due to the lack of unitary for the non-Hermitian systems. Here, the non-Hermitian dynamics is characterized by the individual quantum trajectories without quantum jumps, which describes physics differently from the Lindblad master equation approach where the quantum jumps occur and the outcomes are averaged out32.

Non-Hermitian skin effect

We first consider the initial state of fermions to be of a charge density wave (CDW) state, and monitor the dynamics of the fermion density \(\left\langle {n}_{r}(t)\right\rangle =\left\langle {{\Psi }}(t)\right\vert {\hat{n}}_{r}\left\vert {{\Psi }}(t)\right\rangle\). In the Hermitian case, fermions propagate reciprocally throughout the system after the global quench. However, when the hopping is nonreciprocal, fermions can be amplified toward one direction and attenuated in the other direction. For the open boundary condition (OBC), see Fig. 2a–c, when h = 0.2, the memory of initial CDW state is lost after the global quench. The fermions propagate to one side leading to the non-Hermitian skin effect, and a approximate domain wall state is formed due to the Pauli exclusion principle. As h is increased to 1.0, a little memory of initial state is preserved because of the effective binary disorder potential, and the localization phenomenon is consistence with the non-Hermitian skin effect. Even when h is as large as 4.0, the trail of non-Hermitian skin effect is still observed. Meanwhile, large fluctuations are also observed on account of the binary nature of the disorder. In the periodic boundary condition (PBC) case, see Fig. 2d–f, the non-Hermitian skin effect disappears, and the localization behavior and fluctuations become more pronounced with the increase of the effective disorder strength h. We also consider the quench dynamics from the initial domain wall (DW) state, the results about non-Hermitian skin effects are shown in Supplementary Note 1. In addition, we also present the dynamics of spin subsystem arising from the CDW and DW initial states in Supplementary Note 2.

Fig. 2: Dynamics of fermion density.
figure 2

Dynamics of fermion density \(\left\langle {n}_{r}(t)\right\rangle\) for the system with length L = 16 under (a–c) open boundary condition (OBC) and (d–f) periodic boundary condition (PBC) at different effective disorder strength h. The initial state of fermionic subsystem is charge density wave (CDW) state and the non-Hermiticity is chosen as g = 0.2. The color bar indicates the values of fermion density.

Full size image

Disorder-free localization-delocalization transition

The Anderson model with the nonreciprocal hopping, which has been investigated by Hatano and Nelson40, exhibits the localization-delocalization phase transition in one-dimensional system. We show that the interplay between the \({{\mathbb{Z}}}_{2}\) gauge field and non-Hermitian skin effect leads to the localization-delocalization phase transition without disorder.

The light-cone behavior exhibited by the connected density correlator is an important signal for diagnosing the localization phenomenon. The connected density correlator for fermions is defined by

$$\begin{array}{rcl}&&{\left\langle {{\Psi }}(t)\left\vert {\hat{n}}_{j}{\hat{n}}_{j+d}\right\vert {{\Psi }}(t)\right\rangle }_{{{{{{{{\rm{c}}}}}}}}}=\left\langle {{\Psi }}(t)\left\vert {\hat{n}}_{j}{\hat{n}}_{j+d}\right\vert {{\Psi }}(t)\right\rangle -\\ &&\left\langle {{\Psi }}(t)\left\vert {\hat{n}}_{j}\right\vert {{\Psi }}(t)\right\rangle \left\langle {{\Psi }}(t)\left\vert {\hat{n}}_{j+d}\right\vert {{\Psi }}(t)\right\rangle ,\end{array}$$
(7)

where d is the separation between two sites. In Fig. 3a, b, we observe the asymmetric light-cone behavior in the evolution but for the strong effective disorder the spreading eventually halts. Particularly, the spreading of correlations is well described by the Lieb-Robinson velocity v = 4J, indicating that the quantum information propagates with a finite velocity52,53. Next, we probe the localization behavior by measuring the average of nearest-neighbor density imbalance,

$${{\Delta }}\rho (t)=\frac{1}{L}\mathop{\sum}\limits_{j}\left\vert \left\langle {{\Psi }}(t)\left\vert {\hat{n}}_{j}-{\hat{n}}_{j+1}\right\vert {{\Psi }}(t)\right\rangle \right\vert ,$$
(8)

which quantifies the average difference in fermion density between nearest-neighbor sites. For a translationally invariant state, this quantity is zero, while in the localized phase, it takes a non-zero value. From Fig. 3c, d, we can see that the Δρ(t) decays to a finite asymptotic value with some fluctuations. The asymptotic value of Δρ(t) and oscillation amplitude both grow with the increase of h and decreases as g increases. In the finite-size scaling displayed in Fig. 3e, f, the asymptotic value of Δρ(t) approaches the thermodynamic value as L becomes larger. The strong disorder strength prevents the delocalization, while the strong non-Hermiticity results in the delocalization, indicating the weak memory effects.

Fig. 3: Dynamics of connected density correlator and density imbalance.
figure 3

a, b Absolute value of connected density correlator \({\langle \psi (t)\vert {\hat{n}}_{j}{\hat{n}}_{j+d}\vert \psi (t)\rangle }_{c}\) of fermions as a function of the separation d and time t for g = 0.2. The dashed line indicates the Lieb-Robinson velocity vLR = 4J describing the spreading of correlations. The color bars quantify the absolute values of \({\langle \psi (t)\vert {\hat{n}}_{j}{\hat{n}}_{j+d}\vert \psi (t)\rangle }_{c}\). Time evolution of density imbalance Δρ(t) after a quench for (c) a range of values h at g = 0.2 and (d) a range of values g at h = 1.0. e, f Final time values of \(\overline{{{\Delta }}\rho }(t)\) averaged from t = 60 to t = 100 for different systems sizes up to L = 16. Thermodynamic values for (e) different h at fixed g and (f) different g at fixed h are labeled near the y-axis. The bars denote the standard error of the mean. All dynamics are measured after a global quench from a charge density wave (CDW) initial state under periodic boundary condition (PBC).

Full size image

Von Neumann entanglement entropy has been widely used to study the proprieties of many-body systems. Its definition is given by

$$\begin{array}{r}S=-{{{{{{{\rm{Tr}}}}}}}}\left[{\varrho }^{{{{{{{{\rm{A}}}}}}}}}\ln {\varrho }^{{{{{{{{\rm{A}}}}}}}}}\right],\end{array}$$
(9)

where the reduced density matrix ϱA is the partial trace of the density matrix ϱ of whole system \({\varrho }^{{{{{{{{\rm{A}}}}}}}}}=T{r}^{{{{{{{{\rm{B}}}}}}}}}\left[\varrho \right]\). If A and B are entangled, then the reduced density matrix must be a mixed state and the von Neumann entanglement entropy measures this mixing. In Fig. 4c, the entanglement entropy of nonequilibrium steady state reaches the maximum at the critical point, and as the length increases the critical point hc ≃ 0.8 is approached, separating the delocalized and localized phases. More results about the dynamics of entanglement entropy of fermion can be found in Supplementary Note 3.

Fig. 4: Phase transitions.
figure 4

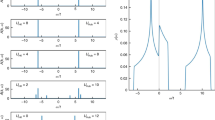
a The single particle localization lengths are obtained from the transfer matrix method as a function of h for the system with L = 200. The bars indicate the statistical errors on the mean of random selection of 2000 charge sectors. b The eigenenergies of the single-particle model with L = 200 for the localized phase g = 0.1, h = 0.6 and delocalized phase g = 0.8, h = 0.6. c Final time value of entanglement entropy of fermions is averaged from t = 500 to t = 1000 for different L, and the entanglement entropy is obtained by averaging over 1000 charge sectors. d Phase diagram of localization-delocalization transition obtained by mapping the averaged values of Δρ(t) (from t = 120 to t = 160) to the parameter space (g, h) for L = 12 with all charge sectors. The delocalization transition lines are displayed from the relation \({g}_{{{{{{{{\rm{c}}}}}}}}}={\lambda }_{{{{{{{{\rm{sp}}}}}}}}}^{-1}\), where λsp is the single-particle localization length. The color bar quantifies the the averaged values of Δρ(t). e Dependence of \({P}_{{{{{{{{\rm{Im}}}}}}}}}\) on (h, g) for the single-particle model with L = 200, the color bar quantifies the values of \({P}_{{{{{{{{\rm{Im}}}}}}}}}\). Eigenenergies of the non-Hermitian Hamiltonian Eq. (4) with L = 12 for a fixed sector \(\left\{1,-1,1,-1,\ldots ,1,-1\right\}\) in the (f) delocalized phase h = 0.2, g = 0.2 and (g) localized phase h = 3.0, g = 0.2. The color of each circle represent the intensity of entanglement entropy of right eigenstate corresponding to the eigenenergy.

Full size image

The aforementioned results provide insight into the impact of the interplay between non-Hermiticity and \({{\mathbb{Z}}}_{2}\) gauge field on the phenomenon of localization-delocalization transition. The dynamical phase paragram is shown in Fig. 4d where the finite final time values of Δρ(t) corresponds to the localized phase. The delocalization line is determined by the localization length that characterizes the localization features. Since the effective Hamiltonian Eq. (4) describes the noninteracting fermions with a binary disorder potential, the localization length of single-particle model also reveals the localization feature. In the non-Hermitian case, g plays the role of an imaginary vector potential that appears in the wave functions of a localized state such that54

$$\begin{array}{r}{\psi }^{{{{{{{{\rm{L,R}}}}}}}}}(r) \sim \exp \left(-\frac{\left\vert r-{r}_{{{{{{{{\rm{c}}}}}}}}}\right\vert }{\lambda }\mp g\left(r-{r}_{{{{{{{{\rm{c}}}}}}}}}\right)\right),\end{array}$$
(10)

where ψL,R(r) are left and right eigenvectors, respectively. rc is its localization center and λ represents the corresponding localization length. If g > λ−1, either ψL(r) or ψR(r) diverges, the wave functions ψL,R(r) no longer represent an exponentially localized state. Therefore, the delocalized transition point is determined by the condition g = λ−1 54,55,56,57. For g < λ−1, the energy spectrum is real and all wave functions are exponentially localized with the same localization length, so that the spectral localization also implies dynamical localization42,58. In Fig. 4a, the single particle localization length, obtained by the transfer matrix method (see Supplementary Note 4)35,59,60, decreases exponentially with the increase of h. The localization length diverges at a critical point hc and the larger g induces the larger hc. As shown in Fig. 4d, the transition line \({g}_{{{{{{{{\rm{c}}}}}}}}}={\lambda }_{{{{{{{{\rm{sp}}}}}}}}}^{-1}\) clearly distinguishes the localized and delocalized phases.

Real-complex transition

It has been discovered that the localization-delocalization transition is accompanied by a real-complex transition of the eigenenergies in the non-Hermitian system32. In order to verify this phenomenon in a disorder-free system, we will examine it utilizing the ratio

$${P}_{{{{{{{{\rm{Im}}}}}}}}}=\overline{{D}_{{{{{{{{\rm{Im}}}}}}}}}/D},$$
(11)

where \({D}_{{{{{{{{\rm{Im}}}}}}}}}\) is the number of eigenvalues with nonzero imaginary parts and D is the total number of eigenvalues. The overline notation indicates the disorder average. We have employed a cutoff of C = 10−13 in the calculation. In Fig. 4b, the spectrum is symmetric around the real axis due to the time-reversal symmetry. In the delocalized phase, the imaginary parts of eigenvalues are nonzero, whereas in the localized phase, they are zero. Figure 4e depicts the phase diagram of real-complex transition which is approximately coincide with the localization-delocalization transition. In the localized phase, almost all the eigenenergies are real due to the strong disorder, while in the delocalized phase they are complex due to the nonreciprocal hopping. The non-Hermiticity leads to the dynamical instability in the delocalized phase. In contrast, the system is stable in the localized phase where the energy is conserved. Consequently, the dynamics are distinct in the two phases, the dynamical localization-delocalization transition closely corresponding to the real-complex transition of eigenenergies.

In Fig. 4f, g, it can be observed that the strong disorder not only suppresses the generation of imaginary parts in almost all eigenenergies, but also enlarges the absolute value of real parts of eigenenergies and leads to the formation of eigenenergy clusters, attributable to the binary nature of the disorder. More intriguingly, the right eigenstates corresponding to the small absolute real or imaginary parts of eigenenergies tend to have larger entanglement entropy regardless of whether they belong to the delocalized or localized phases.

Non-Hermitian quantum disentangled liquids

The interacting mixture of heavy and light particles has been recognized as a factor that can induce a dynamical form of localization, where the heavy particles act as a source of disorder for the light ones. From the perspective of entanglement, the multiple subsystems consisting of the heavy and light particles may behave diverse dynamics, with some undergoing thermalization, while others do not, which is described by a phase of matter known as quantum disentangled liquid19,61,62. It is natural to inquire whether the quantum disentangled liquid can persist in the non-Hermitian system. In order to explore this problem further, we will reveal the long-time quench dynamics of quantum mutual information of the original degrees of freedom, namely the f-fermions and S-spins. For the OBC case, we divide the system into three partitions, as depicted in Fig. 5a, to ensure equal sizes for the two subsystems A and B. The quantum mutual information between subsystems A and B is defined as

$$I({{{{{{{\rm{A}}}}}}}}:{{{{{{{\rm{B}}}}}}}})={S}^{{{{{{{{\rm{A}}}}}}}}}+{S}^{{{{{{{{\rm{B}}}}}}}}}-{S}^{{{{{{{{\rm{AB}}}}}}}}}$$
(12)

where SA and SB are the von Neumann entanglement entropy for A and B, respectively. The SAB denotes the von Neumann entanglement entropy of composite system A ⋃ B. The presence of non-zero quantum mutual information indicates a correlation between the subsystems A and B.

Fig. 5: Features of non-Hermitian quantum disentangled liquid.
figure 5

a The partitioning methods of the whole system. Dynamics of quantum mutual information for the fermion and spin subsystems with different sizes at the localized phase (b–d) h = 1.0, g = 0.1 and delocalized phase (e–g) h = 0.5, g = 0.6. The initial state is the charge density wave state for fermion and the z-polarized state for spins. Saturation values of quantum mutual information of fermion \(\overline{{I}_{{{{{{{{\rm{f}}}}}}}}}(t)}\) and spin \(\overline{{I}_{{{{{{{{\rm{S}}}}}}}}}(t)}\) are averaged from t = 103 to t = 106 for different systems sizes. Here the open boundary condition is considered.

Full size image

In the localized phase (see Fig. 5b–d), it is observed that the quantum mutual information of nonequilibrium steady states of fermions remains independent of the system size, reaching a saturation point governed by the area law, \({I}_{{{{{{{{\rm{f}}}}}}}}}(t\to \infty ) \sim {L}_{{{{{{{{\rm{AB}}}}}}}}}^{\dim -1}\). This behavior can be attributed to the strong \({{\mathbb{Z}}}_{2}\) gauge field, which causes the fermion wave function to resemble a product state with low entanglement, indicating that the fermions are disentangled. In contrast, the long-time dynamics of quantum mutual information of spins depends on the system size and follows a volume law scaling, \({I}_{{{{{{{{\rm{S}}}}}}}}}(t\to \infty ) \sim {L}_{{{{{{{{\rm{AB}}}}}}}}}^{\dim }\), as shown in Fig. 5c. This distinct behavior, where the light particles (fermions) fail to thermalize and reside in a disentangled area law phase due to the presence of the heavy particles (spins), serves as a prominent characteristic of quantum disentangled liquid.

In the delocalized phase, as illustrated in Fig. 5e–g, the fermions and spins respectively exhibit the area law scaling and volume law scaling, which implies that the quantum disentangled liquid retains despite the strong non-Hermiticity. This result challenges the conventional understanding that the delocalized phase is characterized by the volume law scaling of quantum correlation. In the closed quantum systems, the particles diffuse throughout the system during evolution, resulting in the thermalization and extensive quantum correlation. However, the non-Hermitian skin effect drives the fermions to propagate to one side and preventing the diffusion of quantum correlation throughout the system. As a result, the fermions are delocalized but not thermalized, and cannot generate the global quantum correlation63. Therefore, the quantum mutual information of fermions obeys the area law rather than the volume law, indicating the presence of quantum disentangled liquid in this delocalized phase.

Although the quantum disentangled liquids exist in both the localized and delocalized phases, their physical essences are completely different. The area law scaling for fermions in localized phase originates from the \({{\mathbb{Z}}}_{2}\) gauge field, while in the delocalized phase, it is the consequence of non-Hermitian skin effect. In general, the quantum disentangled liquid shows its robustness to the non-Hermiticity. It is worth emphasizing that this phenomenon is independent of the segmentation method used for the whole system. Even if the sizes of segments A and B are not equal, it is still observable (see Supplementary Note 5). Especially, the area law of quantum mutual information has recently been experimentally verified in an ultracold atom simulator64. Therefore, the non-Hermitian quantum disentangled liquid may be observed in the ultracold atom simulator through the diverse scaling behaviors of quantum mutual information.

Flow of quantum information

We further study the dynamics of entanglement entropy of fermion and spin subsystems to explore the effect of non-Hermiticity on the quantum mutual information. In the presence of non-Hermiticity, as shown in Fig. 6a, b, the growth of the entanglement entropy \({S}_{{{{{{{{\rm{f}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}(t)\), \({S}_{{{{{{{{\rm{f}}}}}}}}}^{{{{{{{{\rm{B}}}}}}}}}(t)\) and \({S}_{{{{{{{{\rm{f}}}}}}}}}^{{{{{{{{\rm{AB}}}}}}}}}(t)\) of fermion is greatly suppressed. The entanglement entropy for the nonequilibrium steady state is smaller than that for the Hermitian case and monotonically decreases with respect to g. Consequently, the quantum mutual information of fermion (see Fig. 6c) initially increases and then decreases as a function of g. Figure 6d shows that the non-Hermiticity has minimal effects on the dynamics of entanglement entropy of spin subsystems \({S}_{{{{{{{{\rm{S}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}(t)\) and \({S}_{{{{{{{{\rm{S}}}}}}}}}^{{{{{{{{\rm{B}}}}}}}}}(t)\), however, the presence of non-Hermiticity significantly diminishes the entanglement entropy of nonequilibrium steady state (see Fig. 6e), which are the mainly reason for the growth of quantum mutual information with the non-Hermiticity, see Fig. 6f. The non-Hermiticity induces the nonreciprocal dissipation of fermion system, causing the quantum information to flow from fermions to spins. Consequently, the quantum mutual information of spin subsystem increases obviously. This result paves the way for the preparation and control of the quantum correlated states in the non-Hermitian systems operating far from thermal equilibrium.

Fig. 6: Dynamics of entanglement entropy and quantum mutual information.
figure 6

Dynamics of entanglement entropy (a) \({S}_{{{{{{{{\rm{f}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}(t)\), \({S}_{{{{{{{{\rm{f}}}}}}}}}^{{{{{{{{\rm{B}}}}}}}}}(t)\), (b) \({S}_{{{{{{{{\rm{f}}}}}}}}}^{{{{{{{{\rm{AB}}}}}}}}}(t)\) and (c) quantum mutual information If(t) of fermion subsystems after a quench from a charge density wave initial state under open boundary condition. Dynamics of entanglement entropy (d) \({S}_{{{{{{{{\rm{S}}}}}}}}}^{{{{{{{{\rm{A}}}}}}}}}(t)\), \({S}_{{{{{{{{\rm{S}}}}}}}}}^{{{{{{{{\rm{B}}}}}}}}}(t)\), (e) \({S}_{{{{{{{{\rm{S}}}}}}}}}^{{{{{{{{\rm{AB}}}}}}}}}(t)\) and (f) quantum mutual information of spin subsystems after a quench from a charge density wave initial state under open boundary condition. Insets are the variation of mean values from t = 103 to t = 106 for the nonreciprocal hopping strength g. All results are obtained under the same conditions L = 10 and h = 1.

Full size image

Discussion

In summary, we have investigated the nonequilibrium dynamics in the non-Hermitian lattice gauge model where the spinless fermion coupled to a \({{\mathbb{Z}}}_{2}\) gauge field formed by the spins on the bonds. We show that the interplay between the non-Hermitian skin effect and the \({{\mathbb{Z}}}_{2}\) gauge field leads to the disorder-free localization-delocalization transition. We have also explored the real-complex transition of eigenenergies which closely corresponds to the localization-delocalization transition. Additionally, by identifying the diverse scaling behaviors of quantum mutual information where the fermions obey the area law and the spins follow the volume law, we have proposed a phase of matter known as the non-Hermitian quantum disentangled liquids, and demonstrated the existence of these disentangled liquids in both the localized and delocalized phases. The area law scaling of fermions in the localized phase is due to the \({{\mathbb{Z}}}_{2}\) gauge field, whereas in delocalized phases it originates from the non-Hermitian skin effect. Moreover, the nonreciprocal dissipation of fermions results in the flow of the quantum information from the fermions to the spins, and induces the growth of quantum mutual information of spin subsystem.

It is worth noting that previous discussions have focused on the localization behavior and quantum disentangled liquid in the Hermitian case (g = 0)18,19,62. However, we want to emphasize that the introduction of non-Hermiticity leads to several intriguing phenomena that are absent in the Hermitian case, such as the non-Hermitian skin effect, the disorder-free localization-delocalization transition and the real-complex transition of eigenenergies. In particular, the non-Hermitian skin effect gives rise to the non-Hermitian quantum disentangled liquid in the delocalized phase, which is completely different from the Hermitian case where the \({{\mathbb{Z}}}_{2}\) gauge field dominates the generation of quantum disentangled liquid. Furthermore, the flow of quantum information from the fermions to the spins, induced by non-Hermiticity, has not been previously discussed.

Experimentally, the implementation of \({{\mathbb{Z}}}_{2}\) lattice gauge fields has been achieved using current technological capabilities6,8,9,14,15,16, including the coupling of bosons and fermions to the gauge field. These experiments offer the high controllability and precise readout, providing a toolbox to realize lots of quantum simulation experiments. In our study, the non-Hermitian system may be experimentally realized using the ultracold atoms in optical lattices, where the coupling of fermions to a \({{\mathbb{Z}}}_{2}\) lattice gauge field is to use the Floquet scheme8,9, and the non-Hermiticity is introduced by the cold atoms with engineered dissipation38,51. Recently, the superconducting circuit has been applied to investigate the emergent \({{\mathbb{Z}}}_{2}\) gauge invariance15 and the quantum evolution under the non-Hermitian Hamiltonians65, which may provide another platform to simulate the non-Hermitian lattice gauge theory. In addition, it is also noteworthy that the electric circuits possess the capability to simulate the U(1) lattice gauge theory66 and nonreciprocal non-Hermitian system67,68, thereby offering a potential alternative for realizing the simulation of fermionic matter coupled to the \({{\mathbb{Z}}}_{2}\) lattice gauge field within a non-Hermitian system. Collectively, these experimental platforms such as cold atoms, superconducting circuits, and electric circuits separately offer distinctive avenues for exploring the lattice gauge fields and non-Hermitian systems. However, a crucial challenge remains in fully implementing the non-Hermitian lattice gauge theories on these experimental platforms. The main obstacle lies in the fact that the lattice gauge theories, which describes the coupling of matter fields to gauge fields, primarily arise in interacting systems, while the non-Hermitian Hamiltonians have thus far been implemented in the context of few-body or noninteracting systems38,51,65. Consequently, the experimental introduction of non-Hermiticity into the lattice gauge theories is still an unresolved challenge in terms of the current experimental techniques. Nevertheless, given the rapid advancement in quantum simulation technologies and the increasing adoption of diverse platforms, it might happen that the non-Hermitian lattice gauge theory can be effectively realized in forthcoming experiments. Recently, the many-body non-Hermitian skin effect has been theoretically investigated in an atom-cavity hybrid system where fermionic atoms in the one-dimensional lattice are subject to a cavity-induced dynamic gauge potential69, which provides another possible scheme to test and verify our results in the interacting system. Furthermore, the advancements in measurement technologies make it possible to experientially access the quantum entanglement and quantum mutual information64,70,71. Once experimental systems closely matching our model can be synthesized, our results will provide valuable insights for interpreting the quantum simulation experiments that probe the disorder-free localization properties and non-Hermitian quantum disentangled liquid.

Methods

In this section, we outline the procedure of duality mapping. Through duality mapping from bond spin \(\hat{\sigma }\) to site spins \(\hat{\tau }\),

$${\hat{\tau }}_{j}^{z}={\hat{\sigma }}_{j-1,j}^{x}{\hat{\sigma }}_{j,j+1}^{x},\quad {\hat{\sigma }}_{j,j+1}^{z}={\hat{\tau }}_{j}^{x}{\hat{\tau }}_{j+1}^{x}$$
(13)

the Hamiltonian Eq. (1) becomes

$${\hat{H}}^{{\prime} }= - J\mathop{\sum}\limits_{i}\left({{{{{{{{\rm{e}}}}}}}}}^{g}{\hat{\tau }}_{i}^{x}{\hat{\tau }}_{i+1}^{x}{\hat{f}}_{i}^{{{{\dagger}}} }{\hat{f}}_{i+1}+{{{{{{{{\rm{e}}}}}}}}}^{-g}{\hat{\tau }}_{i}^{x}{\hat{\tau }}_{i+1}^{x}{\hat{f}}_{i+1}^{{{{\dagger}}} }{\hat{f}}_{i}\right)\\ - h\mathop{\sum}\limits_{i}{\hat{\tau }}_{i}^{z},$$
(14)

which is equivalent to the original one only on a restricted Hilbert space. It can be identified that the charges \({\hat{q}}_{j}={\hat{\tau }}_{j}^{z}{(-1)}^{{\hat{n}}_{j}}\) with \({\hat{n}}_{j}={\hat{f}}_{j}^{{{{\dagger}}} }{\hat{f}}_{j}\) are local conserved and generate the \({{\mathbb{Z}}}_{2}\) gauge symmetry. By introducing a spinless fermion operators \({\hat{C}}_{j}={\hat{\tau }}_{j}{\hat{f}}_{j}\), the effective Hamiltonian Eq. (4) can be obtained.

We choose the tensor products of fermion and spin states \(\left\vert {{{\Psi }}}_{0}\right\rangle ={\left\vert S\right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}\otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{f}}}}}}}}}\) as the initial state. In order to investigate the dynamics of fermions on the dual language, the initial state is transformed to the one in the Hilbert space of the \(\hat{C}\) degrees of freedom. If we choose the fermion states as the Fock states, i.e., \({\left\vert \psi \right\rangle }_{{{{{{{{\rm{f}}}}}}}}}={\hat{f}}_{i}^{{{{\dagger}}} }\cdots {\hat{f}}_{j}^{{{{\dagger}}} }\left\vert {{{{{{{\rm{vacuum}}}}}}}}\right\rangle\), then the states have the same form for \(\hat{C}\) fermions \({\left\vert \psi \right\rangle }_{{{{{{{{\rm{C}}}}}}}}}={\hat{C}}_{i}^{{{{\dagger}}} }\cdots {\hat{C}}_{j}^{{{{\dagger}}} }\left\vert {{{{{{{\rm{vacuum}}}}}}}}\right\rangle\). In this article, the spin states are restricted to the z-polarized state \({\left\vert S\right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}=\left\vert \uparrow \uparrow \uparrow \cdots \,\right\rangle\). From the duality transformation, we can obtain that

$${\hat{\tau }}_{i}^{x}{\hat{\tau }}_{j}^{x}{\left\vert \uparrow \uparrow \uparrow \cdots \right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}=\mathop{\prod}\limits_{i}{\hat{\tau }}_{i}^{z}{\left\vert \uparrow \uparrow \uparrow \cdots \right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}={\left\vert \uparrow \uparrow \uparrow \cdots \right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}},$$
(15)

where the relation \({\left\vert \uparrow \uparrow \uparrow \cdots \right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}=\frac{1}{\sqrt{2}}({\left\vert \to \to \cdots \right\rangle }_{{{{{{{{\rm{\tau }}}}}}}}}+{\left\vert \leftarrow \leftarrow \cdots \right\rangle }_{{{{{{{{\rm{\tau }}}}}}}}})\) has been used. Then the initial state form \({\left\vert S\right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}\otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{f}}}}}}}}}\propto {\left\vert S\right\rangle }_{{{{{{{{\rm{\tau }}}}}}}}}\otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{C}}}}}}}}}\) can be identified. Next, the τ spins can be replaced by the conserved charges,

$${\left\vert \uparrow \uparrow \uparrow \cdots \right\rangle }_{{{{{{{{\rm{\sigma }}}}}}}}}\otimes \left\vert \psi \right\rangle =\frac{1}{\sqrt{{2}^{N-1}}}\mathop{\sum}\limits_{\left\langle {\tau }_{i}\right\rangle =\uparrow \downarrow }\left\vert {\tau }_{1},{\tau }_{2},\cdots \,\right\rangle \otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{C}}}}}}}}},$$
(16)

where \({\vert \to \rangle }_{{{{{\uptau }}}}} = ({\vert \uparrow \rangle }_{{{{{{{{\rm{\tau }}}}}}}}}+{\vert \downarrow \rangle }_{{{{{\uptau }}}}})\) for each τ spin and the sum is over all charge configurations. Taking a single state \(\vert {\tau }_{1},{\tau }_{2},\cdots \, \rangle \otimes {\vert \psi \rangle }_{{{{{{{{\rm{C}}}}}}}}}\) as an example, the fermion state is the tensor product of site occupation, this single state is rewritten as

$${\left\vert {(-1)}^{{n}_{1}}{\tau }_{1},{(-1)}^{{n}_{2}}{\tau }_{2},\cdots \right\rangle }_{{{{{{{{\rm{q}}}}}}}}}\otimes {\left\vert \psi \right\rangle }_{{{{{{{{\rm{C}}}}}}}}}.$$
(17)

At the initial state, since the occupation numbers are fixed, only a common sign structure is contributed. Therefore, the initial state is transformed into a dual representation, see Eq. (5). In this work, we used QuSpin for simulating the dynamics of the systems72,73.