Abstract
Nanostructure arrays such as nanowire, nanopillar and nanocone arrays have been proposed to be promising antireflection structures for photovoltaic applications due to their great light trapping ability. In this paper, the optical properties of Si nanopillar and nanocone arrays in visible and infrared region were studied by both theoretical calculations and experiments. The results show that the Mie resonance can be continuously tuned across a wide range of wavelength by varying the diameter of the nanopillars. However, Si nanopillar array with uniform diameter exhibits only discrete resonance mode, thus can't achieve a high broadband absorption. On the other hand, the Mie resonance wavelength in a Si nanocone array can vary continuously as the diameters of the cross sections increase from the apex to the base. Therefore Si nanocone arrays can strongly interact with the incident light in the broadband spectrum and the absorbance by Si nanocone arrays is higher than 95% over the wavelength from 300 to 2000 nm. In addition to the Mie resonance, the broadband optical absorption of Si nanocone arrays is also affected by Wood-Rayleigh anomaly effect and metal impurities introduced in the fabrication process.
Similar content being viewed by others
Introduction
Structures by architectural design at the nanoscale to provide high optical absorbance are important for improving the efficiency of solar cells. In addition to interference-based antireflection coating, silicon-based two-dimensional array of nanostructures, such as nanosphere, nanowire, nanopillar and especially nanocone, have recently been demonstrated as promising building blocks for high efficiency solar cells due to their broadband low reflectivity for light1,2,3,4,5,6,7,8. These nanostructure arrays could be utilized to enhance absorption and to reduce reflectivity in solar cells without introducing extra materials. Since the nanostructure arrays can be added to the outer side of the solar cells, they do not affect the internal morphology of the active-layer. Silicon nanostructures with high absorbance in visible and near infrared region have been reported9,10. Besides applications in solar cells, textured silicon with excellent antireflection ability could also be utilized in hetero-junction photovoltaic cells, photothermal devices and supersensitive photo-detectors. The low reflectivity of Si nanostructure arrays has been attributed to many different factors, including the graded-index coating model2,11,12 with the mechanism similar to that of the multilayer anti-reflection thin film model, multiple light scattering13,14 where the nanostructure arrays enhanced the scattering (or absorption) path length and substrate-coupled by Mie resonance4,15 which was usually used to describe small aspect-ratio particles.
Nanostructures can be made in a variety of shapes and sizes which can significantly influence optical properties of the nanostructure arrays16,17,18. The effects of substrate on the optical properties of Si nanoparticles have also been studied in previous works19,20,21. Most theoretical studies so far have focused on nanosphere or nanopillar arrays. However, Si nanocone arrays with high absorbance in a wide wavelength range have recently been reported9,10. Understanding the optical response of nanostructure arrays to solar radiation is still a critical and fundamental step in the design of future generations of high performance solar cells.
In this paper, the optical properties of Si nanopillar and nanocone arrays in visible and infrared region were studied by theoretical calculations and experimental measurements. By simulating the reflectance and absorbance spectra and the electric field distributions of Si nanostructure arrays, we demonstrated that the Mie resonance modes can be tuned by the cross section diameters from the apex to the base in Si nanocone arrays, which resulted in high absorption over a wide range of solar spectrum. It was also shown that the nanocone arrays can act as optical antenna while the incident light is coupled to the Si substrate by the Mie resonance absorption, which increases the efficiency of the solar cells.
Results and Discussion
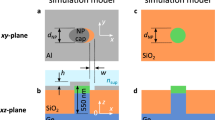
Fig. 1(a) and (b) illustrate the configuration of nanopillar and nanocone arrays used in the simulations. The array is defined by three parameters: base diameter BD, period P and height H. For nanocone arrays, the base diameter is always set equal to the period. All arrays were illuminated from the top in air. The incident direction of light is normal to the substrate surface unless otherwise specified.
Two different nanopillar array samples were fabricated with H = 150 nm and P = 500 nm, the base diameters are 150 nm and 190 nm, respectively. Fig. 2(a) shows the atomic force microscope (AFM) image of fabricated nanopillar sample with H = 150 nm, P = 500 nm and BD = 190 nm. The measured and simulated reflectance spectra of the nanopillar samples are shown in Fig.2(b), the measured results are in good agreement with the simulations except for the wavelength lower than 500 nm. The discrepancy between experimental and simulated results may be caused by the different dielectric constants between the doped Si (in experiments) and intrinsic Si (in the simulations)22. With increasing diameter, the dip (700 nm for BD = 150 nm sample and 850 nm for BD = 190 nm sample) of reflection resulting from the Mie resonance shows a trend of redshift. Fig. 2(c) and (d) illustrate the simulated reflectance and absorbance spectra of silicon nanopillar arrays with the same period and height but different diameters. The sharp drop in the reflectance around 500 nm is due to Wood-Rayleigh (WR) anomaly effect caused by the periodic structure. WR anomaly occurs when the array period P and wavelength λ satisfy the following equation23:

where n is the refractive index of the optical medium, k is the order of WR anomaly and θ is the incident angle. For normal incident of light into Si nanopillar arrays, n = 1 and θ = 0, the equation becomes P = kλ. So the dip near 500 nm in Fig. 2(c) is the first order of WR anomaly. In Fig. 2(b) the incident angle is 8 degree so the wavelength of WR is near 570 nm.
Mie resonance and absorbance spectra of the Si nanopillar arrays.
(a) AFM image of the nanopillar sample with BD = 190 nm, H = 150 nm, P = 500 nm. (b) Average value of transverse electric (TE) and transverse magnetic (TM) modes from the simulations is compared with experiment; the incident angle is 8 degree. (c,d) Simulated reflectance and absorbance spectra of silicon nanopillar arrays with different diameters. (e) Electric field distributions (|E|/|E0|) of Si nanopillar arrays in (b), the diameter is 190 nm. (f) Qsca of the Si nanopillar with different effective radius. Mie resonance peaks redshift with the effective radius of nanopillar.
Other dips at the wavelengths of 662, 699, 847 and 927 nm in Fig. 2(c) and (d) can be attributed to the Mie resonance effect at base diameter of 135, 150, 190 and 210 nm, respectively24,25. The redshift of Mie resonance modes with increasing particle size is predicted from the simulations. The electric field distributions in Fig. 2(e) provide useful information for understanding the light propagation in the structure. Light at the resonant wavelength is trapped and confined in the pillar and then spreads into the substrate. Fig. 2(f) illustrates the normalized scattering cross section (Qsca) of the nanopillar arrays with different effective radii. The two red narrow bands represent the first order of the Mie resonance26. The two modes are magnetic dipole (MD) and electric dipole (ED) resonance labeled in the figure. It can be seen that the peaks of Mie resonance could be adjusted by controlling particle parameters. Although Mie resonance effect helps lowering the reflectance of nanopillar arrays, the reflectance is still much higher than that of silicon nanocone structure.
It has been reported that Si nanocone structure can have high absorbance in visible to near infrared wavelength range9,10. This observation is contradictory to the fact that monocrystalline silicon is transparent in the infrared region. To further understand the absorption of nanocone structure in visible and infrared region, the simulations were performed by including the extinction coefficient from the metal silicides through the effective medium approximation (EMA)27 in the infrared region. In this case, the metal silicides are iron and chrome silicides which formed in the surface layer of the nanocone during the samples fabrication. Detailed information for the nanocone sample can be found in recent publication by Qiu et al9. The monocrystalline Si nanocone structure was also simulated for comparison. Fig. 3(a) and (b) show a bird's eye view and corresponding cross sectional scanning electron microscope (SEM) image of the prepared silicon nanocone arrays, respectively. The nanocone sample shows certain degree of irregularity. By counting individual particles through SEM image, the nanocone sample is 179.5 ± 18.6 nm in base diameter and 460.4 ± 35.7 nm in height. In order to see the influence of non-uniform nanocone arrays on the optical property, simulations for nanocone arrays with randomness in the heights and base diameters were performed for comparison. The structure (named as “case 1”) is a periodic array consists of 4 nanocones in the unit cell with different heights and diameters (i.e., D1 = 200 nm, H1 = 420 nm, D2 = 160 nm, H2 = 440 nm, D3 = 160 nm, H3 = 460 nm D4 = 200 nm, H4 = 480 nm), as illustrated in Supplementary Fig. S3(c). The average base diameter and height of “case 1” are close to those of the experimental sample. As shown in Supplementary Fig. S3(d), the spectrum of “case 1” is smoother and broader than the one from uniform size array. The measured spectrum in the experimental sample is an average over the spectra of various particle sizes and leads to a smooth curve. Fig. 3(c) and (d) give the absorbance and reflectance spectra of “case 1” with and without EMA. The EMA introduced a strong absorbance in infrared region, indicating that the strong absorbance observed by experiment in the infrared region is due to the introduction of impurities during the sample fabrication. For monocrystalline silicon, the light with the wavelengths greater than 1000 nm will penetrate the substrate. Impurities and defects in the sample increased the scattering within the sample and the light was trapped, thus reduced the reflectance and enhanced the absorption in the infrared region. In the visible region, the differences between EMA and monocrystalline silicon are negligible, so EMA will not be taken into account in discussions below.
Simulations were also performed to compare the optical response of an isolated nanocone and that of a nanocone array with the same size of 160 nm in base diameter and 300 nm in height. The Qsca spectra are shown in Fig. 4(a). It is has been shown that conical structures have very similar scattering properties as nanopillars in Fig. 2(f). Furthermore, the compact periodic structure strongly affects the wavelength of Mie resonance. The resonance peaks of nanocone arrays merge into a broader and much stronger feature at 500–1000 nm range, which is in agreement with previous works on nanoparticles16,17. The Qsca and reflectance spectrum (on Si substrate) of nanocone arrays are compared in Fig. 4(b). The reflectance reaches to a minimal value when Qsca is maximal. The electric field distribution in Fig. 4(c) demonstrates how light was coupled to the substrate by Mie resonances (substrate in this figure is 200 nm thick). With the diameter of the cross section changes continuously from the base to the apex, light with every wavelength could find an optimum resonance condition in nanocone arrays. This leads to the reflectance lower than 2.5% in the whole spectrum and much better performance than nanopillar structures. The resonance mode in the cone overlaps with the substrate and provides a leaky channel for light coupling into the substrate. Because most light will be scattered forward or absorbed, the efficiency of solar cells using the nanocone arrays as the anti-reflection layer will be increased. Besides nanocone structure, other particles with gradual diameter variations could also have the potential to achieve a high broadband absorbance.
Mie resonance and absorbance spectra of the Si nanocone arrays.
(a) Normalized scattering cross section of single Si nanocone (black) and Si nanocone array (red). (b) Relationship between reflectance (black) and normalized scattering cross section (red) of Si nanocone arrays. (c) Electric field distributions (|E|/|E0|) of Si nanocone arrays at different wavelength, the nanocone is 300 nm in height and 160 nm in base diameter. (d,e) Simulated absorbance spectra of Si nanocone arrays of various heights and base diameters. The arrows indicated the Mie resonance peaks.
The Mie resonances of particle arrays are controlled by particles sizes and the periodicity of the arrays28,29. We have also simulated the dependence of the absorbance on the height and period of nanocone arrays. Fig. 4(e) shows the absorbance of nanocone arrays with different base diameters (or periods); the height is fixed at 400 nm. For periodic nanocone arrays, changing the period does not show significant effects on average absorbance as illustrated in Supplementary Fig. S4(b). But the peaks from Mie resonance (indicated by the arrows) exhibit significant redshift as the base diameter increased. The results of absorbance with the height at the fixed period is shown in Fig. 4(d), the periods of the nanocone arrays are fixed at 160 nm and the height varies from 300 nm to 500 nm. The average absorbance increases with the height, which is enhanced by the larger surface area of the particles30. However, the redshift of Mie resonances (marked with arrows) are hardly observed as the height of the nanocones vary from 300 to 500 nm. The effective radius of nanocone particle with different height is given in Supplementary Table 1. The effective radius is limited by the period and the Mie resonance peak shows little trends of shifting. In Fig. 4(d) and (e), there are other sharp peaks other than Mie resonance peak. For BD = 160 nm, the peak is at 413 nm and is shifted as the base diameter (or period) changes. These peaks can be explained by WR anomaly discussed above (see Eq (1)). More details about the origins of all peaks in Fig. 4(e) are given in supplementary Table 2. Absorbance and reflectance (average value of TE and TM modes) spectra simulated for Si nanocone array with P = BD = 160 nm, H = 400 nm at different light incident angles are also shown in Supplementary Fig. S5. The results show that the Si nanocone array exhibits broadband and quasi-omnidirectional (angle of incidence from 0 to 60°) antireflection property.
Conclusions
In summary, Si nanopillar and nanocone arrays with various heights and base diameters were investigated by simulations and experiments. The simulations indicate that the high absorbance of the nanostructure arrays is due to the Mie resonance and WR anomaly effect, which could be tuned by changing the parameters of the nanostructures. The electric field distributions and the large normalized scattering cross section (Qsca) associated with the Mie resonance modes reveal that coupling of the Mie resonance modes with the Si substrate leads to a strong light trapping effect. The Mie resonant wavelength can be tuned continuously as the diameters of the cross sections in nanocone increase from the apex to the base, resulting in a broadband absorption. The presence of impurities in the nanostructures is beneficial to broaden the absorption to the infrared region. The dependence of these resonances on the geometries of nanostructure arrays provides useful controlling parameters in designing specific wavelength and bandwidth photovoltaic and photothermal devices.
Methods
Fabrication and Measurement
The nanopillar samples were fabricated by reacting ion etching and the nanocone sample was fabricated using heavy-metal incorporated low-energy Ar+ ion sputtering method12. The ion beam faced normally to the polished side of the Si sample. The Si sample was fixed by a stainless steel mask consisting of Fe and Cr with a hole of diameter of 1.5 cm in the middle. The reflectance and transmittance spectra of the samples were measured using a UV-vis spectrometer (Perkin Elmer, Lambda 950 with integrating sphere) with non-polarized light source. The surface topography was measured using an Atomic Force Microscope System (Veeco, VT-1000) and Scanning Electron Microscope (Philips, XL30).
Optical Modelling and Simulation
The reflectance and absorbance spectra of the nanostructure arrays are simulated using the transfer matrix method (TMM)31,32. The TMM software package was developed by Iowa State University Research Foundation. It can handle the wave scattering by nanostructure arrays, leading to the transmission and reflection spectra. The nanostructure arrays are modeled using the periodic boundary conditions in the in-plane directions. The reflectance and absorbance were calculated with arrays on a 500 μm thick Si substrate. In our simulation, the nanocone structure is approximated by a series of stacking cylinders as shown in Supplementary Fig. S2.
The DDSCAT 7.2 code package was employed to calculate normalized scattering cross section (Qsca), normalized absorption cross section (Qabs) and the electric field distributions33. The DDSCAT package is based on the discrete dipole approximation (DDA); the target is replaced by an array of point dipoles. The electromagnetic scattering problem for an incident wave interacting with this array of point dipoles is then solved. For targets with a substrate, the DDA will consume much longer time because each point of the substrate will be replaced with a dipole. In this case, the thickness of substrate in electric field distribution calculation (Fig. 2(e) and Fig. 4(c)) was set to 200 nm. The quantity being plotted in the electric field distributions is the electric field E normalized to the intensity of incident light E0 (i.e. |E|/|E0|).
The dielectric constant of silicon used in the simulations was taken from a book by Palik34.
References
Peng, K., Wang, X. & Lee, S.-T. Silicon nanowire array photoelectrochemical solar cells. Appl. Phys. Lett. 92, 163103 (2008).
Zhu, J. et al. Optical absorption enhancement in amorphous silicon nanowire and nanocone arrays. Nano Lett. 9, 279–282 (2008).
Chattopadhyay, S. et al. Anti-reflecting and photonic nanostructures. Mat. Sci. Eng. R 69, 1–35 (2010).
Spinelli, P., Verschuuren, M. & Polman, A. Broadband omnidirectional antireflection coating based on subwavelength surface Mie resonators. Nat. Commun. 3, 692 (2012).
Wang, H. P. et al. Periodic Si nanopillar arrays by anodic aluminum oxide template and catalytic etching for broadband and omnidirectional light harvesting. Opt. Express 20, A94–A103 (2012).
Hsu, C. M. et al. High Efficiency Amorphous Silicon Solar Cell on a Periodic Nanocone Back Reflector. Adv. Energy Mater. 2, 628–633 (2012).
Wang, B. & Leu, P. W. Enhanced absorption in silicon nanocone arrays for photovoltaics. Nanotechnology 23, 194003 (2012).
Hua, B., Wang, B., Yu, M., Leu, P. W. & Fan, Z. Rational Geometrical Design of Multi-diameter Nanopillars for Efficient Light Harvesting. Nano Energy 2, 951–957 (2013).
Qiu, Y., Hao, H. C., Zhou, J. & Lu, M. A close to unity and all-solar-spectrum absorption by ion-sputtering induced Si nanocone arrays. Opt. Express 20, 22087–22094 (2012).
Huang, Y. F. et al. Improved broadband and quasi-omnidirectional anti-reflection properties with biomimetic silicon nanostructures. Nat. Nanotechnol. 2, 770–774 (2007).
Xi, J. Q. et al. Optical thin-film materials with low refractive index for broadband elimination of Fresnel reflection. Nat. Photonics 1, 176–179 (2007).
Zhou, J., Hildebrandt, M. & Lu, M. Self-organized antireflecting nano-cone arrays on Si (100) induced by ion bombardment. J. Appl. Phys. 109, 053513–053515 (2011).
Muskens, O. L., Rivas, J. G., Algra, R. E., Bakkers, E. P. & Lagendijk, A. Design of light scattering in nanowire materials for photovoltaic applications. Nano Lett. 8, 2638–2642 (2008).
Garnett, E. & Yang, P. Light trapping in silicon nanowire solar cells. Nano Lett. 10, 1082–1087 (2010).
Cao, L. et al. Semiconductor nanowire optical antenna solar absorbers. Nano Lett. 10, 439–445 (2010).
Evlyukhin, A. B., Reinhardt, C. & Chichkov, B. N. Multipole light scattering by nonspherical nanoparticles in the discrete dipole approximation. Phys. Rev. B 84, 235429 (2011).
Van de Groep, J. & Polman, A. Designing dielectric resonators on substrates: Combining magnetic and electric resonances. Opt. Express 21, 26285–26302 (2013).
Evlyukhin, A. B. et al. Demonstration of magnetic dipole resonances of dielectric nanospheres in the visible region. Nano Lett. 12, 3749–3755 (2012).
Fofang, N., Luk, T., Okandan, M., Nielson, G. & Brener, I. Substrate-modified scattering properties of silicon nanostructures for solar energy applications. Opt. Express 21, 4774–4782 (2013).
Evlyukhin, A. B., Reinhardt, C., Evlyukhin, E. & Chichkov, B. N. Multipole analysis of light scattering by arbitrary-shaped nanoparticles on a plane surface. J. Opt. Soc. Am. B: Opt. Phys. 30, 2589–2598 (2013).
Markovich, D. L., Ginzburg, P., Samusev, A., Belov, P. A. & Zayats, A. V. Magnetic dipole radiation tailored by substrates: numerical investigation. Opt. Express 22, 10693–10702 (2014).
Aspnes, D., Studna, A. & Kinsbron, E. Dielectric properties of heavily doped crystalline and amorphous silicon from 1.5 to 6.0 eV. Phys. Rev. B 29, 768 (1984).
Rayleigh, L. Note on the remarkable case of diffraction spectra described by Prof. Wood. Phil. Mag. 14, 60–65 (1907).
Bohren, C. F. & Huffman, D. R. Absorption and scattering of light by small particles, Bohren, C. F. & Huffman, D. R. (ed.) 83–129. (John Wiley & Sons, Inc., New York, 1998).
Rahachou, A. & Zozoulenko, I. V. Light propagation in nanorod arrays. J. Opt. A: Pure Appl. Opt. 9, 265 (2007).
Bezares, F. J. et al. Mie resonance-enhanced light absorption in periodic silicon nanopillar arrays. Opt. Express 21, 27587–27601 (2013).
Bruggeman, D. Dielectric constant and conductivity of mixtures of isotropic materials. Ann. Phys.(Leipzig) 24, 636–679 (1935).
Evlyukhin, A. B., Reinhardt, C., Seidel, A., Luk'yanchuk, B. S. & Chichkov, B. N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 82, 045404 (2010).
Kuznetsov, A. I., Miroshnichenko, A. E., Fu, Y. H., Zhang, J. & Luk'yanchuk, B. Magnetic light. Sci. Rep. 2, 492 (2012).
Kelzenberg, M. D. et al. High-performance Si microwire photovoltaics. Energ. Environ. Sci. 4, 866–871 (2011).
Li, M. et al. Higher-order incidence transfer matrix method used in three-dimensional photonic crystal coupled-resonator array simulation. Opt. Lett. 31, 3498–3500 (2006).
Li, M. et al. Perfectly matched layer absorption boundary condition in planewave based transfer-scattering matrix method for photonic crystal device simulation. Opt. Express 16, 11548–11554 (2008).
Draine, B. T. & Flatau, P. J. User Guide for the Discrete Dipole Approximation Code DDSCAT 7.2. arXiv preprint arXiv 1202.3424 (2012).
Palik, E. D. Subpart 2, Semiconductors. Handbook of Optical Constants of Solids. Palik, E. D. (ed.) 547–569 (Academic press, New York, 1998).
Acknowledgements
Thanks to the insightful discussions with T.N. Zhang, Y. Zhang, X.C. Song and Y. Qiu. The work at Fudan university was supported by National Basic Research Program of China (No. 2010CB933703 and 2012CB934303), Natural Science Foundation of China (Grant No. 11174058, 11374055, 61275160 and 61427815), the No. 2 National Science and Technology Major Project of China (No. 2011ZX02109-004) and the Fudan High-end computing center. Work at Ames Laboratory was supported by the US Department of Energy, Basic Energy Sciences and Division of Materials Science and Engineering, including a grant of computer time at the National Energy Research Scientific Computing Centre (NERSC) in Berkeley, CA under Contract No. DE-AC02-07CH11358.
Author information
Authors and Affiliations
Contributions
Z.Y.W. and S.Y.W. carried out the theoretical analyses; Z.Y.W., R.J.Z. and X.C. performed the optical measurements and surface topography characterization; M.L. synthesized the Si nanocones arrays; Z.Y., K.M.H. and C.Z.W. developed the TMM algorithms and helped theoretical analyses; Y.X.Z. and L.Y.C. discussed and interpreted the results; and Z.Y.W., S.Y.W., C.Z.W., R.J.Z. and Z.Y. co-wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
SUPPLEMENTARY INFO
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Wang, Z., Zhang, R., Wang, S. et al. Broadband optical absorption by tunable Mie resonances in silicon nanocone arrays. Sci Rep 5, 7810 (2015). https://doi.org/10.1038/srep07810
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07810
This article is cited by
-
Large Dense Periodic Arrays of Vertically Aligned Sharp Silicon Nanocones
Nanoscale Research Letters (2022)
-
Semiconductor nanowire metamaterial for broadband near-unity absorption
Scientific Reports (2022)
-
Tuning higher order electric field resonances in plasmonic hexagonal arrays by oxygen-plasma treatment
Applied Physics B (2021)
-
An Investigation on a Crystalline-Silicon Solar Cell with Black Silicon Layer at the Rear
Nanoscale Research Letters (2017)
-
Thin cylindrical slot in an optical microdisk cavity for sensing biomaterials
Applied Physics A (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.