Abstract
The advancement of various fields of science depends on the actions of individual scientists via the peer review process. The referees' work patterns and stochastic nature of decision making both relate to the particular features of refereeing and to the universal aspects of human behavior. Here, we show that the time a referee takes to write a report on a scientific manuscript depends on the final verdict. The data is compared to a model, where the review takes place in an ongoing competition of completing an important composite task with a large number of concurrent ones - a Deadline -effect. In peer review human decision making and task completion combine both long-range predictability and stochastic variation due to a large degree of ever-changing external “friction”.
Similar content being viewed by others
Introduction
Peer review is one of the cornerstones of modern scientific practice. Though various fields of science exhibit a wide variety of ways this is implemented, they generally use the same central idea: anonymous scientists consider a manuscript and then each in charge writes a referee reply summarizing the merits and weaknesses. The editor of the scientific journal acts then. Sometimes the manuscript is published directly, sometimes after further improvement and review and sometimes it is rejected.
Currently the referee process is under a constant flux due e.g. to the concomitant development of electronic (-only) scholarly journals1. The publication practices of scientific journals might need to be reshaped due to such pressures2. It is a long-standing question as to how such refereeing practices can guarantee a fair degree of objectivity3,4,5,6,7,8,9,10,11,12,13. The path from a request by a journal editor to review a certain paper to the final submitted referee report is very similar to many other activities, as for instance maintaining a correspondence. Here, we consider the task-completion of referees by looking at review processes in journals Journal of High Energy Physics (JHEP) and Journal of Statistical Mechanics: Theory and Experiment (JSTAT). We are particularly interested in how the recommendation given by the referee affects the review dynamics.
Clearly a manuscript to be reviewed presents an “important task” in the daily life of a scientist. It takes place simultaneously with other daily activities, including non-professional ones. It is susceptible to a similar analysis recently undertaken for e-mail, text message and ordinary letter correspondence14,15,16,17,18, where classical human activity models based on Poissonian statistics are questioned in favor of power-law statistics14,16,19,20. The idea is that it might be so that human response dynamics do not have any particular time-scale. Text message data18 has been described by a combination of exponential and power-law distributions. This is motivated by an interplay of Poisson-like initiation of tasks, decision making for task execution and interactions among individuals that influence the dynamics. The peer-review process has as such been analyzed on the level of publication processing times, i.e. the time it takes for a manuscript to appear from the initial submission21,22.
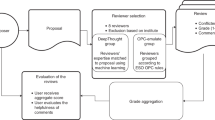
Our analysis is based on two sets of data from the electronic-only journals JHEP and JSTAT (http://jhep.sissa.it; http://jstat.sissa.it), with 7908 and 2558 review requests leading to a referee report, respectively, each from roughly a three-year period. Each entry contains the following information about the review process: preprint id-number, preprint submission date, id-number of the referee to whom the preprint is assigned, date the preprint is assigned by editor, date the referee accepted the assignment (if accepted), date the referee declined the assignment (if declined), date the report was sent, version number of the preprint and the editor's decision. The whole process is illustrated in Figure 1a. If a preprint was assigned to several referees, each is described with a separate entry. All dates are shifted with a random interval to protect anonymity.
How to measure the processing of a manuscript.
a) Editorial process in JSTAT and JHEP. b) Review process durations for both journals. Left: t(E) – t(A), right: t(E) – t(B). c) Total duration τ histogram of the review process (t(E) – t(A)) for both journals after rescaling both distributions with their respective mean values.
Results
Figure 1b depicts the distributions of the total waiting time t(A)–t(E) (left)22,21 and t(B)–t(E) (right, time interval between the assignment of a given manuscript to a given referee and the date the referee report is sent) for both journals. We immediately see that the idea of the referee response solely determining the shape of waiting time distribution is not justified. Fig. 1c shows again the distribution of t(A)–t(E), in units where time is rescaled with the mean waiting times. The both journals appear to have similar characteristics.
A referee report is produced so that an incoming request is replied to with a report, in contrast to correspondence where messages are not always answered. Here, the referee gets reminders automatically; 21 (JSTAT) or 28 (JHEP) days after the assignment. The reports can be classified indirectly using the resulting editor's decision. There are a few possible outcomes: accepted, accepted with minor corrections, to be revised, rejected and not suitable for the journal, denoted below by I, II, III, IV and V, which last case is quite rare and is in the following omitted from consideration.
One important question is whether the day-to-day variation has an influence on the statistical properties (Fig. 2a). A review typically takes much more time than a week, so considering the data it appears that it does not matter when, during a week, such a request is made. This is in spite of the fact that the request-statistics vary over a 7-day cycle. When left free to allocate a given period of time between completing easy and difficult tasks, it has been found in psychology that people tend to allocate more time for the easy ones23. Does a referee write the easier reports (say for those manuscripts that are the very good and those clearly not original or rigorous enough) faster? We split the data into “immediate replies” during the two first days and the rest. Results in Fig. 2b support this idea, since the fraction of both accepted and rejected submissions is higher among reports from the first, fast case. This means that verdicts where the manuscript will need to be elaborated more due to the improvements to be suggested are less frequent.
Data of the waiting times for referee reports.
a) Weekday cyclicity (none): Cumulative distributions of waiting times t(A) – t(E) for manuscripts submitted on different weekdays for both journals., b) Fractions of various decision: classes accepted (I), accepted with minor revision (II), to be revised (III), rejected (IV), not appropriate (V) from all reports (as an inset the same for short-duration processes) c) Waiting time distribution P(t(B) – t(E)) for 1st versions of manuscripts (left) and higher versions (right), d) Dependence of the review duration (t(B) – t(E)) on the verdict and journal. Distributions are scaled with the mean durations.
The waiting time statistics are found to be dependent on the version of the manuscript (Fig. 2c). For JSTAT, 43% of the manuscripts are sent after the editorial decision to the authors for revision whereas for JHEP the figure stands at 30%. The waiting times for second or higher versions are not surprisingly generally shorter. Fig. 2d depicts the distributions for various verdicts. The average waiting times (JSTAT and JHEP) are for the various cases: I: 11.2 days; 15.0 days, II: 17.4 days; 22.0 days, III: 19.8 days; 23.4 days and IV: 17.1 days; 21.7 days. The data implies that JHEP has in general longer response times than JSTAT. For the first round referee reports the differences are not very great among various cases. However, for later, revised versions, it is clear that reports which need to contain constructive criticism (accepted with minor revision, to be revised) are again much slower to do. This feature is similar to that seen for the immediate replies. JHEP and JSTAT have similar statistics after rescaling with the average report waiting time and as indicated by the averages for any particular decision the associated distribution has its specific character. In particular the distributions are not of a power-law, scale-free type.
To account for the observations and the fact that people generally tend to switch between tasks23,24 we construct and apply an event-based model (Methods) based on multitasking: the work on a manuscript is constantly mixed with competing activities. This is formulated based on two kinds of competing tasks, both Poisson processes with equal duration times. Task R is related to reviewing a manuscript and task O means doing something else. Tasks are executed until a sufficient amount of R-tasks is completed to finish the review. A central assumption that we make is that the bias in the completion times is manifest only in the number of tasks of any kind, whether O or R, to be given attention to prior to finishing the report. To give attention does not mean finishing the task at hand of course. We also take into account the inbuilt remainder system both journals use, inducing a Deadline. The details (Methods) mean, that no refereeing-related (R) tasks are done before a certain time related to the journal-induced timescale has passed.
Simulated data is shown with the original data separately for each final verdict type and journal in Fig. 3. The choice λ = 96 implies roughly a 15-minute average duration for a single task (R/O), leaving two free parameters, p1 and p2, for each verdict-journal combination. For JSTAT and JHEP the four cases I…IV can be grouped as pairs of values for p1, p2 for the first and subsequent refereeing rounds as (0.0008, 0.0016), (0.0014, 0.0004), (0.0012, 0.0004) and (0.001, 0.0008) and for JSTAT as (0.0008, 0.0016), (0.0014, 0.0006), (0.0014, 0.0004) and (0.001, 0.0008). To fit the model the four different cases have similar parameters for similar decisions for the two journals. The different versions of manuscripts have quite different waiting times - as noted since a referee has already once read the paper. The model does not include the natural circadian rhythm, so if we discount one third of the total daily time for sleep, we arrive at a 10 minute average duration for a single task.
The event model against data.
We show the aggregate cumulative distributions (for first and further rounds of refereeing). The data is depicted for the four main categories (accepted, accepted with minor revision, to be revised, rejected). To compare with, the empirical first round average response times are (for JSTAT and JHEP, respectively) (I: 23 days 12.5 h; 27 days 12 h), (II: 17 days 22.5 h; 22 days 10.5 h), (III: 21 days 10.5 h; 22 days 16.3 h) and (IV: 20 days 22 h; 24 days 10 h), respectively.
Discussion
The typical values of pi indicate that the review process consists of the order of a thousand subtasks, with a geometric distribution. Not all of these steps imply refereeing: those steps are embedded in the total activity such that a series of tasks …OOOROOROO…R is equivalent to …OOOOOOROO…R. The single tasks to be completed include reading the draft, writing the report etc. but these are interrupted by tasks that demand execution (meetings, working on own projects, shopping for groceries…). For each manuscript the number of tasks that need to be completed varies according to how familiar referee is with the subject, how busy he/she is with his/her own work, what is the general quality of the submission and so forth - that is, it also is related to the verdict.
The dynamics of refereeing can be described by a geometric summation scheme based on asymmetric Laplace law. Similar kinds of models find applications25 when studying phenomena of cyclic nature. Both the data and the model indicate refereeing is described by a “Deadline effect”: the task has to be completed in the presence of competing noise. Thus it is different from correspondence patterns and the statistics of referee report completion do not have scale-free features. Broad power-law distributions are excluded by the need to complete the report.
The contribution of a referee is a crucial factor determining the duration of a review process. Fig. 1b shows that the shape of the waiting time distribution is different if one considers the whole review time compared to expectation from the time taken by the referee alone. Therefore, the time taken by the editor to process a given manuscript is also dependent on the “quality” of the paper. The statistics of the times it takes for the editor to send the manuscript to a referee (t(B)-t(A)) correlate also with the final verdict and are free of such a clear Deadline feature as seen in the referee statistics. Such waiting times are probably in the case of JSTAT and JHEP a result - often - of lengthy searches of willing referees. One should recall the common practice that authors suggest referees or to exclude certain persons that they think might have a negative prejudice about the work or authors. This has been indicated to have a positive effect on getting published26. Note that the original selection of the referee may well be influenced by the expectations of the editor, who thus have their important role27.
Considerations of waiting times and their origins are related to the important issue of detecting fraud6. One could for instance ask, what do the features we see here imply about letting simply bad or even fraudulent manuscripts get published? Certainly our model includes a specific effect that is related to the control mechanisms of JSTAT and JHEP, the reminders that are sent in other words.
The dynamics of the process are correlated with the final verdict. In other words, it is easier to review a manuscript that seems at a first glance “better” and this manifests as a bias in the under-pressure situation of a continuous stream of decisions whether to proceed with tasks related to the report. Note that the microscopic time scale λ is chosen in our simulations similar for all O's and R's. The correlations between the measured statistics and the final verdict present the question: is the determinism it implies a result of a subjective referee bias, or that the expert referee follows a justifed, educated guess from the beginning? We think that taken as a trend, the causality implies the latter.
Methods
The decision model describes the properties of tasks R and O and decides when the review process is finished. We implement a scheme which implies a geometric summation of independent and identically distributed random variables, giving rise to asymmetric Laplace distributions28. We start with the assumption where both tasks R and O are identical Poisson processes with an exponentially distributed duration time. Thus we are left with a process where the random variable describing the duration of the review process - for each verdict separately – is

where  ~ Uniform(0, t0), Ti ~ Exponential(λ) and Nj ~ Geom(pj) (j = 1, 2, see below). The parameter t0 for both journals was interpreted to be the time interval after which a remainder for the referee is automatically sent - 21 days for JSTAT, 28 days for JHEP (independent best trial fits arrive surprisingly enough at close values of t0, data not shown).
~ Uniform(0, t0), Ti ~ Exponential(λ) and Nj ~ Geom(pj) (j = 1, 2, see below). The parameter t0 for both journals was interpreted to be the time interval after which a remainder for the referee is automatically sent - 21 days for JSTAT, 28 days for JHEP (independent best trial fits arrive surprisingly enough at close values of t0, data not shown).
For second and higher versions, we omit the  to make the resulting distribution fit the exponential waiting time distribution (presented in log-log-scale in Fig. 2c). Thus for both journals we have model parameters t0, λ, p1 and p2. To test the model an event-driven simulation is run with the following steps. i) Draw a uniform random number
to make the resulting distribution fit the exponential waiting time distribution (presented in log-log-scale in Fig. 2c). Thus for both journals we have model parameters t0, λ, p1 and p2. To test the model an event-driven simulation is run with the following steps. i) Draw a uniform random number  with mean t0/2, ii) Draw a geometric random number ν1 with mean 1/p1. iii) Draw and sum up with
with mean t0/2, ii) Draw a geometric random number ν1 with mean 1/p1. iii) Draw and sum up with  ν1 exponential random numbers with mean 1/λ. iv) Draw a uniform random number r between 0 and 1. v) If the value of r is smaller than f (f is the fraction of manuscripts sent for revisions), draw a geometric random number ν2 with mean 1/p2. If not, return to i). vi) Continue summing with drawing ν2 exponential random numbers with mean 1/λ and with
ν1 exponential random numbers with mean 1/λ. iv) Draw a uniform random number r between 0 and 1. v) If the value of r is smaller than f (f is the fraction of manuscripts sent for revisions), draw a geometric random number ν2 with mean 1/p2. If not, return to i). vi) Continue summing with drawing ν2 exponential random numbers with mean 1/λ and with  , Return to ii) and repeat N-1 times. The sampling by simulations was chosen to be the same as in the empirical data i.e. 7908 review events for JHEP and 2558 for JSTAT, respectively. Each simulation was repeated 100 times and the parameters pi were varied to obtain the best fit in each case.
, Return to ii) and repeat N-1 times. The sampling by simulations was chosen to be the same as in the empirical data i.e. 7908 review events for JHEP and 2558 for JSTAT, respectively. Each simulation was repeated 100 times and the parameters pi were varied to obtain the best fit in each case.
References
Azar, O. H. The slowdown in first-response times of economics journals: Can it be beneficial? Econ. Inq. 45, 179–187 (2007).
Boldt, A. Extending ArXiv. org to Achieve Open Peer Review and Publishing. J. Schol. Publish. 42, 238–242 (2011).
Altschuler, E. L. Peer reviews: in praise of referees. Nature 473, 452 (2011).
Bornmann, L., Weymuth, C. & Daniel, H. D. A content analysis of referees' comments: how do comments on manuscripts rejected by a high-impact journal and later published in either a low- or high-impact journal differ? Scientometr. 83, 493–506 (2010).
Bornmann, L. & Daniel, H. D. Reviewer and editor biases in journal peer review: an investigation of manuscript refereeing at Angewandte Chemie International Edition. Res. Eval. 18, 262–272 (2009).
Bornmann, L., Nast, I. & Daniel, H. D. Do editors and referees look for signs of scientific misconduct when reviewing manuscripts? A quantitative content analysis of studies that examined review criteria and reasons for accepting and rejecting manuscripts for publication. Scientometr 77, 415–432 (2008).
Campanario, J. M. & Acedo, E. Rejecting highly cited papers: The views of scientists who encounter resistance to their discoveries from other scientists. J. Am. Soc. Inf. Sci. Tech. 58, 734–743 (2007).
Wilson, R. ‘Referee factor’ would reward a vital contribution. Nature 441, 812 (2006).
Bedleian, A. G. The manuscript review process - The proper roles of authors, referees and editors. J. Manag. Inq. 12, 331–338 (2003).
Campanario, J. M. Peer review for journals as it stands today - Part 1. Sci. Comm. 19, 181–211 (1998).
Campanario, J. M. Peer review for journals as it stands today - Part 2. Sci. Comm. 19, 277–306 (1998).
Campanario, J. M. Consolation for the scientist - Sometimes it is hard to publish papers that are later highly-cited. Soc. Stud. Sci. 23, 342–362 (1993).
Blank, A. F. The effects of double-blind versus single-blind reviewing - experimental evidence from the American Economic Review. Amer. Econ. Rev. 81, 1041–1067 (1991).
Barabási, A.-L. The Origin of Bursts and Heavy Tails in Human Dynamics. Nature 435, 207 (2005).
Malmgren, R. D., Stouffer, D. B., Motter, A. E. & Amaral, L. A. N. A Poissonian explanation for heavy tails in e-mail communication. Proc. Nat. Acad. Sci. USA 105, 18153–18158 (2008).
Oliveira, J. G. & Barabási, A.-L. Darwin and Einstein Correspondence Patterns. Nature 437, 1251 (2005).
Malmgren, R. D., Stouffer, D. B., Campanharo, A. S. L. O. & Amaral, L. A. N. On Universality in Human Correspondence Activity. Science 325, 1696 (2009).
Wu, Y., Zhou, C., Xiao, J., Kurths, J. & Schellnhuber, H. J. Evidence for a Bimodal Distribution in Human Communications. Proc. Nat. Acad. Sci. USA 107, 44 (2010).
Jo, H.-H., Karsai, M., Kertesz, J. & Kaski, K. Circadian pattern and burstiness in mobile phone communication. New J. Phys 14, 013055 (2012).
Walraevens, J., Demoor, T., Maertens, T. & Bruneel, H. Stochastic queueing-theory approach to human dynamics. Phys. Rev. E. 85, 021139 (2012).
Jo, H.-H., Pan, R. K. & Kaski, K. Time-varying priority queuing models for human dynamics. Phys. Rev. E85, 066101 (2012).
Mryglod, O., Holovatch, Y. & Nryglod, I. Editorial process in scientific journals: analysis and modeling. Preprint arXiv:1109.6211.
Payne, S. J., Duggan, G. B. & Neth, H. Discretionary task interleaving: Heuristics for time allocation in cognitive foraging. J. Exp. Psych.: Gen. 136, 370–388 (2007).
Gonzáles, V. M. & Mark, G. Managing currents of work: multi-tasking among multiple collaborations. ECSCW 2005, Proceedings of the Ninth European Conference on Computer-Supported Cooperative Work, 1822 September 2005, Paris, France., 143–162 (2005).
Kalashnikov, V. Geometric Sums: Bounds for Rare Events with Applications. Springer (New York), 1997.
Grimm, D. Suggesting or Excluding Reviewers Can Help Get Your Paper Published. Science 309, 1974 (2005).
Fischer, C. C. Editor as good steward of manuscript submissions: ‘Culture,’ tone and procedures. J. Schol. Publ. 36, 34–42 (2004).
Kotz, S., Kozubowski, J. & Podgórski, K. The Laplace distribution and generalizations: a revisit with applications to communications, economics, engineering and finance. Birkhäuser, Boston. (2001).
Acknowledgements
The Academy of Finland's Center of Excellence - program is thanked for funding. The authors are grateful to the JSTAT and JHEP editorial office personnel and technical staff. Prof. Marc Mézard should be thanked for support as the JSTAT Chief Scientific Director.
Author information
Authors and Affiliations
Contributions
T.H. analyzed the data and run the model simulations. M.A. had the main responsibility for manuscript writing.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Hartonen, T., Alava, M. How important tasks are performed: peer review. Sci Rep 3, 1679 (2013). https://doi.org/10.1038/srep01679
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01679
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.