Introduction

Microfluidics allows to manipulate and control flow of small quantities of liquids1,2. The field is evolving at a rapid pace and has the potential to influence diverse subject areas from chemical synthesis and biological analysis to optics and information technology. However microfluidics is still not used on a large scale3, which is at least in part due to the complex equipments these systems rely on. Specifically, for a growing number of applications there is a large demand for flow control and pumping methods in such microchannels4. As a consequence, micropumping has become one of the main developing areas in microfluidics and lab-on-a-chip technology. There have been many pumping methods explored for moving the fluid inside microchannels5,6,7,8,9, but most of these still need rather complex and often large external equipments.

Passive pumps, in which fluid is transferred through microchannels by taking advantage of its intrinsic properties such as surface tension, molecular diffusion or osmotic pressure are the simplest example of micropumps for microfluidic applications. However the main question here remains how to control the flow. We here investigate a simple passive pump consisting of a microchannel with the in/outlets connected to water droplets of different sizes (volumes). Putting two droplets of different size at the in/outlet of a microchannel, there will in general be a flow from the smaller droplet into the larger one due to the Laplace pressure difference. If the two drops have the same contact angle, due to its smaller radius of curvature, the smaller of the two droplets generates a larger Laplace pressure γ/R, with R the radius of curvature and γ the liquid-vapor surface tension; the Laplace pressure difference then drives the flow. This should therefore result in a flow from the smaller drop into the larger one10,11,12,13 and the flow will only stop once the smaller drop has been pumped entirely into the larger one14,15,16. That this need not always be the case, depending on the wetting properties, follows from an explicit calculation of the Laplace pressure. If the drops are spherical caps, the pressure can be written as , where Rw and θ are the radius of contact line area and contact angle respectively, two experimentally controllable parameters. The dependence on the contact angle is interesting since the sine function and hence the Laplace pressure is maximum at θ = 90°. Therefore, flow from a larger drop, i.e. the one with larger volume, into a smaller one is in principle possible by manipulating the contact angles. Notably, if the contact angle of the larger drop is close to 90° and the small drop is of similar size but has a significantly smaller contact angle, a flow from the large into the small droplet should be expected. Although the basic idea that the flow is controlled by the radius of curvature and not the drop size is of course well established10,11, we show here how it can be used for passive and active pumping.

Results

We study 2 drops on a PDMS microchannel. Due to the pinning of contact line the shrinking or growing of a droplet may happen either at constant contact area or at constant contact angle. Combining the possibilities for each droplet there are 4 possible situations. In our experiments we observe three that happen consecutively in time. First Phase: In the beginning of the process, the contact areas remain constant for both drops, but the contact angles change. Second Phase: The smaller droplet has fixed contact area but the contact angle of the larger drop has reached the advancing contact angle θadv = 110°; therefore the contact area starts to increase at constant contact angle (Supplementary Fig. S1). Third Phase: The smaller drop has reached the receding contact angle θrec = 46° and its contact area starts to decrease at fixed contact angle. The important observation here is that this sequence happens because the receding contact angle is significantly smaller than the advancing one (Supplementary Fig. S1). The contact angle, after having gently deposited a drop, is θ = 107° on our PDMS substrate. Therefore, starting from this angle, the larger droplet will reach its advancing contact angle much sooner than the smaller drop reaches its receding contact angle (Fig. 1(d) and (e)). This is also the reason why ‘phase 4’ is not observed in our experiments. The experimental data for the three different phases compare favorably to the numerical solutions of the Stokes equation (see Methods) for the geometry considered here (Fig. 1(b)–(g)). The favorable comparison shows that solely the wetting properties of the drops determine the flow speed and hence, inversely, controlling the wetting properties allows to control the flow. An example of this is that we can create an unusual flow from a larger into a smaller droplet (Fig. 2). To achieve this, we make a drop of volume V1 and another one with a smaller volume V2, but put the larger droplet on a hydrophobic Teflon surface, so that θ1 ~ 90°. The smaller drop is on a hydrophilic glass surface; we thus have Rw1 ≲ Rw2 but sinθ2 < sinθ1. Under these initial conditions, the pressure in the larger droplet will be larger (P1 > P2) and backflow will occur, as is indeed observed in the experiments (Fig. 2(a)–(c)). In these experiments the initially larger drop has a constant contact radius (Rw1), i.e. the contact line is pinned and the initially smaller one has a constant contact angle (θ2). The results of analyzing our movies made by a fast CCD camera operating at 125 frames/s plotted along with the numerical solutions are shown in Fig. 2(d). It follows that the larger the difference in wetting properties of the two surfaces beneath each drop, the more likely it is to observe backflow. A few examples of the numerics are shown in Fig. 3, where we consider the second phase (θ2, Rw1 = const), with V1 > V2 initially and plot the pressure difference ΔP, as a function of the ratio of the volumes, V1/V2. Backflow occurs when ΔP = P1 − P2 is positive and ; therefore the plots in Fig. 3 show that for smaller values of the contact angle of the initially smaller drop, backflow is more readily observed. This shows that the wetting properties can be used as a method for active pumping.

Figure 1
figure 1

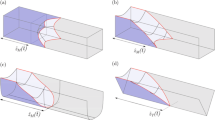
a) Picture of the cylindrical micro-channel in PDMS.b), c) The heights, d), e) the contact angles f), g) the contact radii of the smaller and the larger droplets respectively. The first phase change happens at t = 2.5 s and the second at t = 9 s. The initial values for the numerics are H1(t = 0) = 1.11 mm, H2(0) = 1.76 mm, Rw1(0) = 0.83 mm and Rw2(0) = 1.28 mm.

Full size image
Figure 2
figure 2

Illustration of the flow from the larger drop into a smaller one (connected by a rectangular microchannel).

The left drop is on glass, the right one on PTFE. a) t = 0.0 s, b) 6.6 s, c) 9.24 s. d) Evolution of the volumes of the two droplets in time. Rectangular channel of width w = 4.2 mm, height b = 0.1 mm and length L = 24.75 mm. We are in “phase 2”, with the constants Rw2 = 1.96 mm for the smaller drop and advancing angle on glass for the larger drop θ1 = θadv = 56°. Lines: numerics.

Full size image
Figure 3
figure 3

ΔP = P1 − P2 as a function of the ratio of the volumes.

The total volume is V1 + V2 = 25 μl and Rw1 = 1.6 mm for all the curves, we are in “phase 2”. For smaller contact angles of the initially smaller droplet (θ2), ΔP is positive in a wider range of V1/V2 > 1, so the backflow can be seen with a larger probability. The grey area corresponds to the range of parameters for which backflow is expected to occur.

Full size image

Electrowetting: bi-directional pumping

To be able to actively control the flow and its direction, we use electrowetting techniques to manipulate the wetting properties of a surface instantly and temporarily17,18,19,20,21,22,23, We use it here for building a bi-directional active pump. Directional control using this micropump with such a simple design can have many applications. For instance, due to its biological compatibility, it is suitable for practical applications in microfluidic systems including micro total analysis systems (μTAS) and lab-on-a-chip systems24,25,26.

Putting an electrode inside a droplet of water and another one underneath an insulating surface, one can apply a voltage difference between the electrodes, which leads to an instantaneous decrease of the contact angle and hence Laplace pressure of the drop. This happens because the charges makes it more attractive for the fluid to wet the surface, due to the polarizability of water molecules27. Therefore, turning the voltage on and off induces an abrupt change of the contact angle and can change the flow direction inside our microchannels.

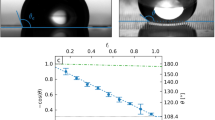
If we have two droplets but the smaller one (left hand side of Fig. 4(a)) has a larger curvature, the flow goes from the smaller droplet to the larger one. Turning on the voltage, due to the electrowetting effect the droplet will spread abruptly, have a larger contact radius and smaller contact angle and hence a smaller Laplace pressure. If we make the curvature small enough (smaller than that of the larger drop on the right hand side), a flow in the reverse direction is indeed observed. Fig. 4(b)–(e) show that at the beginning of the experiment, the drop on the left hand side is evidently smaller and has a smaller curvature than the drop on the right and a flow from left to right is observed. Turning on the voltage (900 V), the smaller drop spreads; the pressure difference ΔP changes sign followed by a change in flow direction. The results for the dynamics compared to the numerical solutions are shown in Fig. 4(f), for an experiment done in “phase 1” for which Rw2 = const and there are two different constant values for Rw1, before and after turning on the voltage.

Figure 4
figure 4

a) Schematic of the bi-directional pumping setup using electrowetting techniques.b) The two drops before turning on the electric potential at t = 0.1 s and c) t = 11.7 s. d) A potential difference of E = 900 V is applied, the contact angle and the direction of flow have changed, t = 15.4 s, e) t = 41.0 s. f) V1, V2 the volumes of the initially smaller and larger drops respectively. The dimensions of the rectangular channel are width w = 2.5 mm, height b = 0.12 mm and length L = 16.3 mm. The electrical potential E = 900 V is turned on at t = 15.2 s. Rw1(OFF) = 1.59 mm, Rw1(ON) = 1.83 mm, Rw2 = 1.69 mm. Lines: numerics.

Full size image

Discussion

In summary, we have shown experimentally that a system of two droplets of different sizes at the ends of a microchannel can behave in three different ways. Considering these different possibilities, we developed a numerical scheme needed for dealing with the system and the importance of the different phases for observing a flow from the larger droplet into the smaller one was shown. In addition, by changing the properties of the surface beneath each droplet we can generate situations in which we get a backflow by choosing the appropriate initial conditions. This provides a different possible interpretation of the experiments by Berthier, Beebe and Ju et al.28,29, who observed backflow in situations similar to the ones described here. They argue that inertia, originating from a rotating flow in the larger droplet, is responsible for the backflow. However, the Reynolds number in their experiment being , where U is the velocity, ρ the density and η the viscosity, casts some doubt on their interpretation of the experiments.

In addition, we have shown by taking advantage of dynamic manipulation of the effective surface properties by electrowetting, that a bidirectional micropump can be made. The possibility of changing the flow direction back and forth by simply turning the voltage off and on, can make the capillary pumping method a powerful tool in microfluidic technologies.

Methods

The first part of our experiments were performed on polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) blocks with a channel, made by pouring the uncured PDMS over a strained wire as a mold and baking it in an oven at 80° for 5 hours. After pulling out the wire through the PDMS, we close the two ends (where the wire was taken out) with small drops of instant glue. We punch two holes perpendicular to the channel through the PDMS for the inlet and outlet. By this method we manufactured cylindrical channels of length L = 25.5 mm and diameter D = 110 μm (Fig. 1(a)). After the channel was filled completely with water, using a syringe, we put two droplets with different sizes (each on the order of few μl) at the outlets of the channel. As the smaller droplet is emptying into the larger one, the height of the droplets and their contact radii were measured by analyzing the movies made with a CCD camera at 20 frames/s.

The backflow experiments were performed on channels made by sandwiching a Parafilm, with the channel carved out in it, between two microscope slides. We used a sand jet perforating technique to make in/outlets through one of the glass slides. To change the wetting properties we attached a layer of Teflon (PTFE) tape around one of the outlets, leaving the other side to be just glass.

The electrowetting setup is sketched in Fig. 4(a). We attach a layer of Teflon tape of thickness 0.25 mm to the upper glass surface, with an aluminized film under the Teflon tape around one of the outlets, that functions as one of the two electrodes.

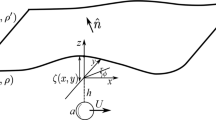
Experimentally, the shapes of the droplets are spherical caps of height H; we need not consider gravity because for all cases considered here the Bond number, is significantly smaller than unity; here g is the gravitational acceleration. For the numerics, we consider two droplets at the outlets of a channel of length L, with the Laplace pressures, P1 and P2 for drops of radii R1 and R2, we have:

For Poiseuille flow, the flow rate is then Q = KchΔP, where for a cylindrical channel and for a rectangular channel , with a channel height b and width w, where w ≫ b. Generally Kch depends on the geometry of the channel and the fluid viscosity. The larger the value of Kch the higher the average flow rate in the channel for a given drop pressure. Therefore this parameter can be used to tune the flux in the microchannel. To quantify the dynamics, we solve the problem numerically. The flow rate is equal to the rate of volume change for each drop, i.e. Q = −dV1/dt = dV2/dt, where generally V1 is the volume of the shrinking droplet (usually the smaller drop) and V2 is that of the growing one (usually the larger one). Combining the above equations we arrive at:

Using trigonometric relations for spherical caps, one can find expressions for the volume of a droplet in terms of two independent parameters such as the height H, the contact radius Rw or contact angle θ of the drop. Therefore, using Eq.(2) for each phase, we will end up with 2 coupled differential equations for the height of the droplet for each phase (see Supplementary). With the initial conditions given by the experiments, we can solve the equations numerically using Runge-Kutta methods.