Introduction

We perform extensive molecular dynamics (MD) simulations of ST2-water in the constant-temperature, constant-pressure ensemble. We equilibrate the system for ≈ 1000 ns for 127 state points in the supercooled liquid region of water. Pressure P ranges from 190 MPa to 240 MPa, while temperature T is as low as T = 230 K at high P and 244 K at low P. We make 624 different simulations, 341 as long as 1000 ns and for four system sizes, N = 216 (80 state points), 343 (75 state points), 512 (44 state points) and 729 molecules (46 state points). For the majority of state points studied we average our results over several (≤ 11) independent runs. We interpolate our data along isobars using the histogram reweighting method1. For , we find that the density ρ decreases sharply within a narrow temperature range, while at lower P it falls off with T continuously. This behavior is consistent with a discontinuous phase transition at high-P between a high-density liquid (HDL) and a low-density liquid (LDL) ending in a liquid-liquid (LL) critical point at lower P (Fig. 1a).

Figure 1
figure 1

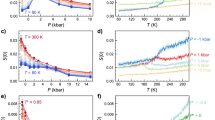
Phase diagram and finite size scaling analysis to locate the line of liquid-liquid (LL) phase transitions.

(a) State points in the P–T diagram simulated. Different symbols correspond to different sizes N. The high-T (red) region exhibits HDL-like states and the low-T (blue) region LDL-like states. In the intermediate (violet) region we observe flipping between HDL-like and LDL-like states. Below the black line Tg correlation times are larger than 100 ns, while above they are smaller and thus equilibrium is attained within reasonable simulation times. The white region, denoted CP, is our estimate of the location of the LL critical point in the thermodynamic limit. (b) Finite-size analysis of Πmin along isobars crossing the discontinuous LL phase transition (violet at high P in (a)) and the Widom line (within the violet region at low P in (a)). At P = 190 MPa, Πmin approaches 2/3 when N → ∞, indicating that the density distribution is unimodal and that one crosses the Widom line and not the line of discontinuous phase transition. At P = 200 MPa, Πmin approaches ≈ 2/3 − 0.001, consistent within its error bar with the value expected at coexistence20. At P = 210 MPa, Πmin tends to a smaller value clearly excluding 2/3 and therefore the distribution is bimodal, that is the fingerprint of a discontinuous LL phase transition. Πmin depends linearly on 1/N to the leading order, displaying deviations only for the smallest size N = 216. The inset shows Π along the isobar at P = 200 MPa as a function of T for all four system sizes (from bottom to top: N = 216, 343, 512, 729) displaying a clear minimum Πmin. Lines are interpolations obtained using histogram reweighting for up to eleven independent simulations of length 1000 ns.

Full size image

This LL critical point was hypothesized2 based on studies of the ST2 model and subsequently studied in detail by many others using, in addition to ST23,4, TIP5P5, TIP4P6, TIP4P-Ew7 and TIP4P/20058 as well as coarse-grained models9,10,11. The existence of the LL critical point allows one to understand X-ray spectroscopy results12,13,14,26 and explains the increasing correlation length in bulk water upon cooling as found experimentally15 and the hysteresis effects16. Holten et al.17,18 reviews available experimental information and shows that the assumption of a LL critical point in supercooled water provides an accurate account on the experimental thermodynamic properties.

Abrupt changes in the global density ρ are related to the appearance of different local structures. Among various parameters describing the local structures we identify d319 and ψ3, defined in the Methods Section, as good quantities to distinguish the LDL and the HDL phase and the best quantities to distinguish them from ice. The average values of ψ3 of the two phases differ by about 50%, the LDL phase being characterized by greater order in the second shell than in the HDL phase.

Liu et al.4, using histogram reweighed Monte Carlo methods in the grand canonical ensemble for only one but quite large system size, find an order parameter distribution function consistent with a critical point belonging to the universality class of a 3 dimensional (3d) Ising model. In Ref.31 Limmer and Chandler question this result using the umbrella sampling method to evaluate the free energy landscape of the ST2 model near a single state point and for a single system size (N = 216). They find two minima in the free energy landscape: one for liquids and one for crystalline structure. They do not find a third minimum corresponding to the LDL and conclude that the LDL does not exist as a metastable state, but only as a transitional state from HDL to crystal. However, Sciortino et al. in33 show, with an implementation of the umbrella sampling with variable number of particles 200 ≤ N ≤ 327 of the umbrella sampling that guarantees very high resolution in the exploration of the free energy landscape, the presence of the minimum corresponding to the LDL state metastable with respect to the crystal, reconfirming the results of Ref.4 and at variance with Ref.31,32. To contribute to the discussion, we present here a finite size scaling analysis of results from extremely long (1µs) MD simulations. We find that 1) LDL is a genuine liquid state, metastable with respect to the crystal, 2) LDL and HDL are separated by a first-order phase transition line ending in a critical point, 3) Close to the LLCP, LDL has relaxation times of the order of 100 ns, which show that 1000 ns runs are sufficient to equilibrate LDL, 4) the results are robust with respect to the finite size scaling analysis and show that the LDL-HDL critical point belongs to the 3 dimensional Ising model.

Results

To show that the LL phase transition exists in the thermodynamic limit, we perform a finite-size analysis along isobars within the supercooled liquid region. For this purpose, we calculate the Challa-Landau-Binder parameter for the bimodality of the density distribution function, 20,21. When is unimodal, Π adopts the value 2/3 in the thermodynamic limit N → ∞, while Π < 2/3 when is bimodal, since two phases coexist (Fig. 1b).

However, for a finite system Π < 2/3 whenever deviates from a delta function. This occurs in the region of the phase diagram where, for a finite system, the isothermal compressibility, KT, has a maximum, i.e., along a locus in the P–T plane that includes (i) the discontinuous (in the thermodynamic limit) phase transition at P > Pc, the LL critical pressure, (ii) the effective LL critical point at Pc(N), where the discontinuity vanishes and (iii) a line for P < Pc that emanates from the LL critical point into the supercritical region. Near Pc this line follows the locus of maxima of the correlation length, known as the Widom line22 and deviates from it at lower P23.

The finite-size behavior of Π allows us to distinguish whether an isobar is above or below Pc20,21 (Fig. 1b). When isobars cross the Widom line (P < Pc), Π displays a minimum Πmin (inset in Fig. 1b) that in leading order approaches 2/3 linearly with 1/N. When consists of two Gaussians of equal weight, i.e. at the coexistence line for , Πmin approaches, also linearly with 1/N, another limiting value where and are the densities of the two coexisting phases20. This limiting value progressively decreases as P increase above Pc, since ρH−ρL increases at coexistence as (P−Pc)β, where β ≈ 0.3 is the critical exponent of the 3d Ising universality class17.

To ensure that the system is in thermal equilibrium, we calculate the correlation time for the first maximum k1 of the oxygen-oxygen intermediate scattering function SOO(k, t), as used in Refs.24 and25 and defined in the Methods Section. While correlation times in the HDL phase are very short (≈ 0.01 ns), they become of the order of 100 ns in the LDL phase, implying that simulations of less than 1 µs are likely affected by poor statistical sampling (Fig. 2). For temperatures above the line Tg in Fig. 1a, correlation times are smaller than 100 ns and we can equilibrate the system within our simulation time.

Figure 2
figure 2

Definition of the correlation time τ0 using the intermediate scattering function.

The correlation time τ0 is calculated using the correlation function COO(k, t) of the intermediate scattering function of the oxygen atoms SOO(k, t). For the k vectors corresponding to the first three maxima k1, k2 and k3 (marked in red, blue and green in the inset), we calculate the evolution of the correlation function COO(ki, τ). We then define the correlation time as the time for which COO(ki, τ) decreases to 1/e for the slowest of the ki vectors. For nearly all the state points k1 has been the vector for which this decrease has been the slowest. We find τ = 10–100 ns for the LDL phase, so we can equilibrate this phase in our simulations of about 1000 ns. Data are for a system of N = 343 molecules at pressure P = 210 MPa and temperatures (from left to right) T = 244 K, 243 K, in the LDL phase and 242 K below the Tg line of Fig. 1a.

Full size image

Figure 3a shows a typical example of a simulation near the critical point for N = 343 molecules at P = 215 MPa and T = 244 K. Here the system exhibits phase flipping between LDL and HDL, with the life-time of each phase distributed from ≈ 20 ns to ≈ 300 ns. This nanoscale phase flipping results in a bimodal density distribution (Fig. 3b) and is observed for all temperatures and pressures around the LL phase transition in a region that shrinks with growing system size.

Figure 3
figure 3

Phase flipping between LDL and HDL at coexistence.

(a) The 1 µs time series shows how frequently, at constant P = 215 MPa and T = 244 K, N = 343 ST2-water molecules switch from LDL-like to HDL-like states. (b) The histogram for the sampled density values, in arbitrary units, after discarding the first 100 ns of the 1 µs time series. For LDL-like states ρ ≈ (0.89 ± 0.01) g/cm3 and for HDL-like states ρ ≈ (1.02 ± 0.03) g/cm3 corresponding to a difference of ≈ 13% in density. Dashed lines are Gaussian best fits of the histogram around the two maxima.

Full size image

Discussion

To estimate the critical exponents of the LL critical point we next investigate the distribution of the order parameter M of the LL phase transition. As for the liquid-gas phase transition27, the order parameter is not simply the density, but a linear combination of the density with another observable28. Here we choose the linear combination of density and energy M ≡ ρ + sE27 and find that it follows, as expected, the behavior of a liquid in the universality class of the 3d Ising model, as is also the case for the liquid-gas transition (Fig. 4). At P = 205 MPa the difference between the maxima and the central minimum of the order parameter distribution is smaller than for the 3d Ising case. At P = 210 MPa it is larger and the critical point therefore seems to be in between, consistent with the conclusion obtained from the analysis of Π. We get the best fit of the order parameter distribution function at a pressure of P = 206 ± 3 MPa and a temperature of T = 246 ± 1 K.

Figure 4
figure 4

The liquid-liquid critical point falls into the same universality class as the liquid-gas critical point.

(a) The distribution function of the rescaled order parameter x ≡ A(M−Mc) where M ≡ ρ + sE with , follows for P = (206 ± 3) MPa and T = (246 ± 1) K (triangles) the order parameter distribution function of the 3d Ising model (solid line)36. The data are from histogram reweighting of N = 343 molecules at P = 205 MPa and T = 246.6 K (squares), P = 206 MPa and T = 246 K (triangles) and P = 210 MPa and T = 245.1 K (circles). We repeat the analysis for (b) N = 512 and (c) N = 729. (d) For large sizes the amplitude A (triangles) scales as A ~ Lβ/v, where β/v ≈ 0.52, as in the 3d Ising universality class27. For corrections to scaling are strong. (e) Contour plot of the distribution of states in the density-energy plane, with red corresponding to the highest values and blue to the lowest. The distribution of the order parameter M ≡ ρ + sE is obtained from this two-dimensional distribution by integrating it with a delta-function δ(M−ρ−sE). We select the value of s for which the distribution of M best fits the distribution of the order parameter for the 3d Ising universality class.

Full size image

The same analysis for N = 512 and 729 yields estimates, consistent with N = 343, of the LL critical point to be Pc = 208 ± 3 MPa and Tc = 246 ± 1 K (Fig. 4b, c). The finite size scaling of the amplitudes of the order parameter distribution A ~ Lβ/v is consistent with the behavior predicted for the 3d Ising universality class with β/v ≈ 0.51827 and strong corrections to scaling for (Fig. 4d).

Finally, we investigate also the possibility of spontaneous crystal nucleation in the LDL phase using the structural order parameter d319. At temperatures below the region of phase flipping, the samples sometimes form large crystallites filling up to 10% of the system volume. Their structure exhibits a mixture of cubic and hexagonal symmetry. However, in approximately 99% of simulations these unstable crystallites vanish within the simulation time of 1000 ns, showing that the free-energy barrier for the crystallization process is significantly larger than kBT in the LDL phase (Fig. 5). We observe irreversible crystallization in only 3 out of 350 (1 µs)–runs, for only N = 343 and all corresponding to state points near the LL critical point (Fig. 1a). This is consistent with the general result that a metastable fluid-fluid phase transition favors the crystallization process in its vicinity29. We did not observe any crystallization events for N = 512 and N = 729 although the total simulation time for these systems is comparable to that of N = 343. The fact that the crystallization rate is not increasing with system size is evidence that LDL is the genuine metastable phase with respect to the stable crystal phase.

Figure 5
figure 5

Example of a simulation where the largest crystallite grows up to 35 molecules and then vanishes in a system having N = 343 molecules at a pressure of P = 200 MPa and T = 246 K.

A molecule i is considered to belong to a crystal if d3(i, j) ≤ dc = −0.87 for three out of its four bonds with nearest neighbors j.

Full size image

In conclusion, we use new methods to investigate both the statics and dynamics of deeply supercooled ST2-water. Specifically, we analyze static quantities (density and potential energy) using the framework of finite-size scaling theory and we analyze the dynamic structure factor over three orders of magnitude of time scales, from 1 to 1000 ns. We find definitive evidence of a first order LL phase transition line between two genuine phases that are each metastable with respect to crystal. The phase transition line terminates in a LL critical point and the exponents associated with this LL critical point are indistinguishable from those expected for a three-dimensional lattice-gas model which is used to describe the liquid-vapor critical point.

Methods

We performed MD simulations in the NPT ensemble using the Stillinger and Rahman34 five-point water model ST2, consisting of five particles interacting through electrostatic and Lennard-Jones forces with a cutoff of 7.8 Å. The pressure was not adjusted to correct for the effects of the Lennard-Jones cutoff, since it would originate from mean field calculations, which become rather poor near a critical point.

We apply the Shake algorithm to constrain the particles inside each molecule. The constant pressure is imposed by a Berendsen barostat and a Nosé-Hoover thermostat is applied to ensure constant temperature35. Periodic boundary conditions have been implemented and reaction field method with a cutoff of 0.78 nm is used for the Coulomb's interactions.

For the simulations we used the following protocol consisting of three steps: (1) For any given density, a constant volume simulation is performed at T = 300 K during 1 ns (first pre-run). (2) The ensemble is then changed to NPT by adding the Berendsen barostat with the desired pressure and the temperature is reduced to T = 265 K, ensuring that the system reaches the HDL phase after 1 ns of equilibration (second pre-run). (3) After these two preruns the system is quenched to the desired temperature, from which the first 100–200 ns are removed as thermalization time. The choice of the thermalization time will be discussed next.

To decide whether the equilibration time is sufficient, we perform two steps. First, we inspect the time series of energy and density to discard the possibility of spontaneous crystallization. In all our NPT simulations we observed only three crystallization events (≈ 1% of total number of runs) all of them in systems with N = 343 molecules. We use them as a reference for the crystal. In a second step we measure the correlation time using the intermediate scattering function.

MD simulations are performed for a finite numbers of state points (Fig. 1a). We use the histogram reweighting method1 to complement the statistics of each state point with the information from nearby state points. Histogram reweighting30 is a method that combines the overlapping histograms of quantities calculated at close-enough state points, reweighting them with an appropriate factor that takes into account the difference in thermodynamic parameters. It is a powerful method that allows to calculate the observables for a continuous range of thermodynamic parameters within those directly simulated.

The order parameter M ≡ ρ + sE is obtained from the distribution in the density–energy plane (Fig. 4e), by integrating it with a delta-function δ(M−ρ−sE). We select the value of s for which the distribution of M best fits the distribution of the order parameter for the 3d Ising universality class. The main effect found when changing s is a small shift in the estimated critical temperature TC of about 0.1 K, which is less than the error of 0.5 K originating from the histogram reweighting.

The oxygen-oxygen intermediate scattering function SOO (k, t) can be used to distinguish between phases of different structure, such as LDL and HDL. We also use it to estimate the correlation time. It is defined as

where denotes averaging over the simulation time t′, is the position vector of the oxygen of molecule l at time t′, k is the wave vector and k is its magnitude |k|. SOO(k, t) describes the time evolution of the spatial correlation along the wave vector k. Since the system has periodic boundaries, the components of k have discrete values 2πj/L, where L is the length of the simulation box and j = 1, 2, .... We define , where average is taken over all vectors k with magnitude k belonging to jth spherical bin , for j = 2, 3, …300.

The temporal decay of SOO(k,t) is characterized by two relaxation times: (i) a short time, τβ, after which SOO(k,t) reaches a plateau SOO(k, τβ) corresponding to the bouncing of the particles inside the cages formed by their neighbors and (ii) a long time, τα, corresponding to a particle escaping from its cage and diffusing away from its initial position. We define the correlation time τ = τα as the time for which , where COO(k, τ) is the structural correlation function (Fig. 2).

We define the bond order parameter d3 following Ref.19. The quantity d3(i, j) characterizes the bond between molecules i and j and is designed to distinguish between a fluid and a diamond structure. It uses the spherical harmonics to identify the tetrahedral symmetry of the diamond structure. In general, each molecule is characterized by a vector in the −dimensional Euclidean space with components and , with

If molecule j belongs to the first coordination shell ni (shell of four nearest neighbors) of molecule i, we define d3(i, j) as the cosine of the angle between two vectors and characterizing the first coordination shells of molecules j and i, respectively:

where

and .

In a perfect diamond crystal d3(i, j) = −1 for all bonds, while for a graphite crystal d3(i, j) = −1 only for bonds connecting atoms in the same layer. For bonds connecting atoms in different layers d3(i, j) = −1/9. Thus in graphite each atom has three out of four bonds having d3(i, j) = −1. In our simulations, the spontaneously grown crystals have many defects, with different parts of the crystals following diamond or graphite patterns (Fig. 6a). Therefore, we consider a molecule in a crystal to have either three or four bonds with d3(i, j) < dc = −0.87, where the value of dc = −0.87 is selected as two standard deviations from the peak of the crystal histogram corresponding to d3 = −1. This is exactly the same criterion to specify molecules in the crystal state as in Ref.19. We find separate crystallites using the percolation criterion, i.e., two molecules satisfying the crystalline criterion belong to the same crystallite if they belong to the first coordination shell of each other (Fig. 5).

Figure 6
figure 6

The equilibrium probability distributions of two different structural parameters that allow us to distinguish among three structures: HDL, LDL and crystal.

(a) For the size of N = 343, in the vicinity of the LL critical point in ≈ 1% of the runs our system spontaneously crystallizes, forming structures with diamond and graphite patterns and with many defects. This structure is well characterized by the probability distribution (line with full dots) of the parameter d3, displaying a large maxima close to d3 = −1, the value that corresponds to the perfect diamond crystal. Another small maximum at d3 = −1/9 corresponds to the bonds connecting different layers in the graphite crystal. For the sake of comparison with the other cases, we divide of the crystal by 10. In the 99% of our simulations we find distributions as those presented here for P = 215 MPa, a pressure above the LL crital point pressure and decreasing T (from right to left). shows an abrupt change when crossing the first-order LL phase transition region at T ≈ 244 K. In particular, displays a pronounced shoulder at higher d3 in the LDL phase and is very different from the crystal case. The arrow marks the value dc = −0.87 selected as two standard deviations from the peak of the crystal histogram corresponding to d3 = −1 as in Ref.19. (b) The equilibrium probability distribution of the single-molecule parameter ψ3 also distinguishes among HDL, LDL and crystal structures. The average values for fluid phases are ψ3 = −0.34 ± 0.19 in the HDL phase and ψ3 = −0.57 ± 0.16 in the LDL phase.

Full size image

We finally observe that by defining as the average of d3 over the four bonds of each molecule, we introduce a single-molecule structural parameter that also can be used to distinguish among the HDL, the LDL and the crystal phase (Fig. 6b).