Introduction

Once only featured in sailors’—mostly disbelieved—stories, rogue waves were first measured only relatively recently: in 1995 at an oil rig in the North Sea1. The concept, namely ocean waves that seem to appear out of nowhere and whose size far exceeds what is considered typical, has been observed or predicted in multiple fields where the wave analogy is applicable: Bose–Einstein condensates2,3, plasmas4,5,6, atmospheric rogue waves7, superfluids8. Optical rogue waves were first reported in 20079. The focus of theoretical research has been on providing generating mechanisms for such extreme behavior10,11,12.

Although with different points of emphasis, extreme and hard-to-predict behavior has been reported and studied considerably longer in other areas of research (see, for example, Pareto’s seminal work on the distribution of wealth from 189613). Further examples include incomes13,14, insurance claims15,16, number of citations of scientific publications17,18,19, earthquake intensities20,21,22, avalanche sizes23, solar flares24, degree distributions of various social and biological networks25,26,27, and many more. Unsurprisingly, the mathematical background of extreme behavior has been most extensively studied with the motivation of mitigating financial risks28,29,30,31,32. This broader area of research is referred to as extreme value theory, and heavy-tailed distributions as well as their estimation play an important role in it.

A rogue wave is, by definition33, an unpredictably appearing wave with an amplitude at least twice as large than the significant wave height, with the tail of the amplitude probability density function (PDF) decaying slower than a Gaussian. While multiple sets of criteria exist33 for using the term rogue wave, a systematic way of estimating and comparing how extreme rogue waves are is needed. The simplest estimators for heavy tails34,35,36 build on the hypothesis that the distribution of interest is such that there exists a sharp, finite threshold beyond which the PDF decays exactly at a power-law rate. This is, of course, in most situations not true, and the basic estimators’ bias can be reduced by taking into account higher-order behavior37.

In comparison with more traditional uses of extreme value theory, non-linear optics38,39 has clear advantages in controllability, reproducibility, and statistical significance of the generated optical extreme events. Optical experiments producing light with heavy-tailed intensity distributions allow high repetition rates and, therefore, large samples to study unstable non-linear phenomena and their sources40,41,42,43. However, obtaining the correct statistics of rogue-wave events is, even so, a non-trivial problem44,45.

The aim of the experiment under consideration46 was to produce highly fluctuating intensities. The authors achieved this in the normal-dispersion regime with a fiber that had a relatively low non-linear refractive index, where such rogue events (without cascading12) were not expected. The reason for the observed level of fluctuations is mainly the super-Poissonian pumping that was applied to the single-mode fiber, which further enhanced intensity fluctuations through nonlinear frequency conversion.

What the literature is lacking is a focus on the essential quantitative description of the measured intensities. Since the size of rogue events can exceed the median by orders of magnitude, their detection is difficult. Any physical measurement device has its limits; this is also the case for optical detectors: the detector response becomes non-linear and saturates with the increase of light power47. For example, for commonly used biased photodiodes, the detector response cannot be larger than the reverse bias voltage; the further increase of input light power leads to the same output. Therefore, detector saturation will almost inevitably spoil the statistics of very energetic rogue events.

Furthermore, the efficiency of an optical non-linear process strongly depends on the intensity of its pump. This is also the case for the experiment under consideration46, where the amount of produced photons and the efficiency of the process depend exponentially on the pump intensity. Thus, the efficiency of supercontinuum generation usually increases with the increase of pump power. However, as soon as the amount of converted pump energy becomes significant (tens of percent), the remaining pump cannot feed the process efficiently anymore; it is already depleted. In this case, increasing input pump power does not increase the output intensity48,49.

The focus of the current work is to tackle the rich phenomenology of optical rogue waves from a non-conventional angle. Instead of concentrating on their origin, our study provides a quantitative description of the measured intensities of optical rogue waves. To this aim, we explore two approaches to adapting the general statistics toolkit for tail estimation (proposed by Rácz and et al.50) to the special case of rogue waves resulting from supercontinuum generation, using data collected during experiments similar to those reported by Manceau and colleagues46. In this reference, an infinite-mean power-law distribution for supercontinuum generation was observed for the first time. However, a detailed statistical analysis of such phenomena requires complementary approaches. Furthermore, we also describe the breakdown of the ideal behavior due to pump depletion and detector saturation.

Results

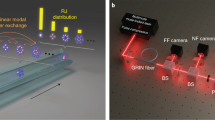
The primary focus of this paper is on estimating the exponent related to the power-law decay of the distribution of measured intensities in the experiment46 whose schematics are shown in Fig. 1. Highly fluctuating super-Poissonian light was used to pump a single-mode fiber in the normal-dispersion regime (see under Experiment in Methods). As a result of these large fluctuations in the pumping light, the observed intensity fluctuations at the other end of the fiber were also quite large in comparison to coherent pumping. In effect, fluctuations in the incoming light were drastically enhanced due to the non-linear effects present in the fiber. Depending on the the orientation of the barium borate (BBO) crystals, the experiment used either non-degenerate parametric down-conversion (PDC) producing light with thermal intensity statistics (exponentially distributed) or degenerate PDC producing bright squeezed vacuum (gamma-distributed intensities).

Fig. 1: Experimental setup.
figure 1

Pulsed 400 nm light is used to pump parametric down-conversion (PDC) in two cascaded barium borate (BBO) crystals. Depending on the phase-matching angle of the crystals, either (a) bright squeezed vacuum (BSV) is generated via degenerate PDC at 800 nm, or (b) thermal light is generated via non-degenerate PDC at 710 nm. These two types of light are filtered by a band-pass filter at 710 ± 5 nm for thermal light or at 800 ± 5 nm for BSV, and used to generate supercontinuum in a single-mode fiber. The resulting intensity is measured (PD) after spectrally filtering the supercontinuum by a monochromator.

Full size image

The current experiment exhibits a spectral broadening in the normal-dispersion regime51 (for further details, check under Experiment in Methods); we refer to this aspect as supercontinuum generation. While this produces less of a broadening effect than in the anomalous-dispersion case, since, to our knowledge, there is no consensus in the literature on exactly what level of broadening constitutes supercontinuum, we will go on using this term throughout the article. Furthermore, rather than spectral broadening, we focus on the amplification effect, which we attribute primarily to four-wave mixing (see Rogue wave generation in Methods). For more details regarding the experiment, see the first two subsections under Methods and the experimental study46.

We will discuss the results for both types of pumping and compare two different approaches to estimating the tail exponent:

  • First, a generalization of the Hill estimator34 introduced in Rácz et al.50, which directly estimates the exponent only (Direct estimation of the tail exponent);

  • Second, fitting a multi-parameter model to the observations (see Tail exponent estimation as part of a model fit), where one of the parameters corresponds to the exponent of interest.

We will also explore the validity of the two approaches and quantitatively describe the intensity distribution where it is affected by both pump depletion and detector saturation (see Supplementary Note 2).

Preliminaries

This section provides a brief summary of terminology and basic quantities; for further details, see Methods and Supplementary Note 3. The results are mainly presented in terms of exceedance probabilities (or complementary cumulative distribution function, or tail function). For a real-valued random variable X, the exceedance probability function (EPF) is defined as the probability that the value of the variable exceeds a pre-defined threshold x:

$$\overline{F(x)}:={{{{{{{\bf{P}}}}}}}}\left(X > x\right),$$
(1)

with \({{{{{{{\bf{P}}}}}}}}\left(\cdot \right)\) denoting the probability of an event. From a finite sample, one can obtain the empirical exceedance probability (EEPF) for any limit x simply as the fraction of observations that exceed x. Empirical exceedance probabilities have multiple advantages over histograms: there is no binning involved; it is smoother; tail behavior is visually more apparent.

The Pareto (or power-law) distribution is the archetype of heavy-tailed distributions and can be given with the PDF \(f(x)={x}_{0}^{-1}{\left(x/{x}_{0}\right)}^{-\alpha -1}\), for x0, α > 0, and x ≥ x0. The constant α is referred to as the tail exponent, and as a measure of tail heaviness, it can be generalized to a broader class of distributions referred to as Pareto-type, or regularly varying distributions. For such distributions, the exceedance probability plot is asymptotically a straight line on a doubly logarithmic scale. As Fig. 2 (yellow lines) shows, our data do not quite behave like this: power-law behavior has an upper limit, which is why alternative approaches are needed to estimate the exponent.

Fig. 2: Heavy tails in intensity fluctuations.
figure 2

We compare different fitting approaches for (a) thermal, and (b) BSV pumping. The yellow line shows the empirical exceedance probabilities (EEPF) from an experimental data set. The red line shows the result of applying the traditional Hill estimator (3) combined with Guillou & Hall’s estimator66 of the tail length k, the red dot marks the beginning of the line. The light blue line (and its dashed extension) shows the result of the generalized version (4) combined with a heuristic choice of the lower and upper cutoff parameters m and M, the light blue dots mark the ends of the interval. The dark blue line (and its dotted extension) show the result of fitting the model (5) to the sample; the value of the upper cutoff was the same as for the generalized Hill estimator and is marked by a dark blue triangle.

Full size image

Thermal pumping

Non-degenerate parametric down-conversion produces light with thermal intensity statistics; that is, in a continuous approximation, the distribution of pumping intensities is exponential.

First, we investigate the properties of the exceedance probability function for intensities observed in supercontinuum generation experiments using a thermal source as a pump (Fig. 2a). Experimental results show that under the investigated circumstances, the single-mode fiber produces exponential amplification, which can be explained in terms of four-wave mixing (see Rogue wave generation and the experimental work46). Since the intensity distribution of the pumping light decays exponentially, after exponential amplification, the resulting intensity distribution should decay at a power-law rate. Visually, the empirical exceedance probability function (at least for the largest values) should be linear on a log-log scale. However, the dependence of the EEPF from experimental data (yellow) seems linear only in the middle section. For low values (below m), this is due to the different types of noises, while for high values (above M), pump depletion affects the distribution in a significant way. It is worth noting that even though we have quite large sample sizes (~105), power-law behavior manifests itself only for the top few percent of observations, so the informative or effective sample size is considerably smaller (~103).

The standard Hill estimator (3) in a realistic experiment is not the best choice of estimation method (red line) since the distribution clearly does not decay at a power-law rate for the largest values, which introduces a significant bias. A better direct estimation can be achieved after discarding the largest observations affected by saturation or pump depletion (that is, estimating the value of the tail exponent from the middle section only) by using the generalized Hill estimator from (4) (light blue line). Finally, we have also used the modeling approach (see Tail exponent estimation as part of a model fit), consisting of constructing a detailed multi-parameter model of the process and estimating its parameters simultaneously, including the one that determines the value of the tail exponent (dark blue line). We can approximate the real process very accurately already with this simple model.

Bright squeezed vacuum

If one uses bright squeezed vacuum (BSV) as a pump instead of thermal light to generate the supercontinuum, the situation remains quite similar (Fig. 2b), but there are also a few significant differences. The difficulty comes from the fact that even though the asymptotic behavior is similar to the thermal case, the convergence to the asymptotics is slower. The Hill estimator (red line) is, as expected, biased as it includes the large, saturated values as well. But if we use the generalized Hill estimator (light blue line) with a properly chosen interval, we can obtain a reasonable estimate even in this case. Note, however, that for this specific measurement, the range within which power-law decay is a reasonable assumption is quite short, about 1%, of the data. The issue is that by using either version of the Hill estimator, one essentially estimates a gamma distribution with an exponential, which works well only asymptotically. However, the largest values are distorted as a result of pump depletion and detector saturation.

This is why the modeling approach can potentially provide more information. The fitted distribution (dark blue line) is not as close to the actual data as for a thermal source. This has a technical reason: in the thermal pumping version of the experiment, fluctuations in the mean intensity of the laser were accounted for by post-selecting the output intensity conditional on the value of the laser intensity. No such post-selection was done in the BSV case, and the model described in Tail exponent estimation as part of a model fit does not take into account fluctuations in the mean incoming intensity. Nevertheless, despite the inaccuracy close to the noise floor, the model sufficiently captures the stretching of the distribution’s tail, which we are ultimately interested in.

Method comparison

Let us highlight the sensitivities of the different methods to choosing the limit(s) of the application interval. Firstly, looking at the direct estimation methods (Fig. 3a) using different lower limits, it becomes more evident why the value of the Hill estimator is rather incidental. For an ideal, strictly power-law distributed sample, the expectancy of the Hill estimator is constant, with its standard deviation decreasing as the number of points taken into account increases. For distributions that are only asymptotically power-law, there is an ideal tail length corresponding to a trade-off between minimizing bias and standard deviation.

Fig. 3: Tail exponent estimates’ dependence on cutoff choices.
figure 3

a Direct fitting methods: \({\hat{\alpha }}_{{{{{{{{\rm{H}}}}}}}}}\left[k(m)\right]\) and \({\hat{\alpha }}_{{{{{{{{\rm{gH}}}}}}}}}\left[k(m),j=100\right]\). b Modeling approach results as a function of the upper cutoff M (all observations below M were taken into account). The blue circles indicate the estimates that were accepted at a 5% significance level by a binomial test, the estimates denoted by yellow circles were rejected (see Supplementary Note 1).

Full size image

A simple approach to estimating this ideal value is looking for a plateau in the Hill plot52, where the estimator’s value is stable. Unfortunately, in our case, the Hill estimator (yellow line in Fig. 3a) presents a clear trend throughout the plotted interval as a function of m due to the bias introduced by the fact that the largest observations are clearly not Pareto-distributed. As a consequence, tail length estimators produce somewhat random values (red points in Fig. 2).

In contrast, throwing out the top observations really makes a difference compared to the standard Hill estimator: the generalized Hill estimator (blue line in Fig. 3a) is much less sensitive to the choice of the lower bound, that is, it produces relatively stable estimates in a wide range of values for m. Note that compared to the traditional Hill estimator, the upper limit M is an extra parameter to choose, which makes this method somewhat more complicated. But in practice, the estimator is also relatively stable in regard of choosing that parameter too, so it is not necessary to have a very accurate estimate of the endpoints of the interval [m, M].

Looking at the sensitivity of the modeling approach (Fig. 3b), we see that the estimates are even more stable with regard to the endpoint of the interval (in this case we only have an upper limit, M). More precisely, this approach provides a similar range of estimates as the generalized Hill estimator, but in addition, we can quantify the fit of the model with the estimated parameters to the measured data, and one can reject the values which are not a good fit (yellow points). And if we only look at the remaining, accepted estimates (blue points), these range only between 1.33 and 1.38 (light blue area), which is a really narrow interval, especially comparing it to the fluctuation of the traditional Hill estimates.

Of course, there is no guarantee that the given estimators are unbiased, so even if they are stable they could give a wrong result. That is why it is generally very useful to have at least two independent estimation methods (which are biased in different ways) and check whether they provide consistent results. We can compare the results of different estimators and can conclude that the modeling approach provides estimates close to the generalized Hill estimator (see Supplementary Table 1). We were interested in seeing if an extended analysis that enables us to use a much larger part of the data can provide an improvement over the generalized Hill estimator, which discards both the smallest and largest observations. If we only look at the estimation of the tail exponent, the answer to this question is no; however, the results of fitting the detailed model provide an independent reference point for the generalized Hill estimator. The fact that the two approaches provide similar estimates increases the confidence in the results. So, in summary, the two approaches are not necessarily meant to compete but rather to complement each other. The advantage of the generalized Hill estimator is that it is easy to compute and is applicable in a broader range of situations as-is, without needing to know the details of the process. The modeling approach, on the other hand, gives us more insight into the specifics of the phenomenon, but at the same time, the exact model applied here is only applicable in a narrow context. This means that a new model should be worked out for the specifics of the process of interest, while the direct approach is applicable out of the box for any process that produces power-law tails.

Breakdown of power-law behavior

As Fig. 2 shows, power-law behavior eventually breaks down; using a semi-logarithmic scale instead of the original log-log (Fig. 4) reveals exactly how: the linear sections in the plots indicate exponential decay rather than power-law (i.e., EEPF ∝ e−λx for some λ > 0). This behavior can be attributed to pump depletion: in the case of a fluctuating pump, the depletion manifests itself not only in the power reduction and decrease of generation efficiency but also in the change of pump statistics46,53. In the presence of pump depletion, the most energetic bursts are not as strongly amplified as weaker ones. The result is that the empirical variance of the intensities is smaller than it would be in the absence of depletion. It is possible to account for this effect in the black-box approach taken in Tail exponent estimation as part of a model fit by altering the response of the fiber (by exchanging the \({\sinh }^{2}\) function for a function that increases exponentially for small values but is only linear for large values), but if one is only interested in the stretching caused by exponential amplification, it is easier to discard the values affected by it. This is what we have done in the previous section. Here, we will also look at the description of the distribution beyond the validity of the power-law functional form.

Fig. 4: Breakdown of power-law behavior.
figure 4

The plots show empirical exceedance probabilities on a semi-logarithmic scale; the samples are the same as shown in Fig. 2, with (a) thermal, and (b) BSV pumping. The same values for the power-law interval [m, M] are indicated by vertical lines. The dark blue solid lines show exponential fits, to observations above 5 ⋅ 104 in the thermal case, and between 2 ⋅ 105 and M* = 106 in the BSV case, providing exponential rate parameter estimates of \({\hat{\lambda }}_{a}=2.6\cdot 1{0}^{-5}\) and \({\hat{\lambda }}_{b}=1.9\cdot 1{0}^{-6}\), respectively. The brown dashed line shows the generalized Pareto fit of the observations beyond M*, with \({\hat{i}}_{\max }=1.58\cdot 1{0}^{6}\) and \(\hat{\gamma }=1.59\).

Full size image

Furthermore, as Fig. 4b shows, if intensities are high enough (beyond about M* = 106), the decay becomes even faster than exponential due to detector saturation. It can be shown (see Supplementary Note 2) that combining an exponential distribution with an exponentially saturating detector results in a generalized Pareto distribution. More accurately, the EEPF is \(\propto {\left({i}_{\max }-x\right)}^{\gamma }\). Here, \({i}_{\max }\) denotes the maximum output of the detector, and γ > 0 the related exponent.

The parameters of the exponential (λ) and the generalized Pareto distributions (\({i}_{\max }\) and γ) can be estimated in a similar fashion to the tail exponent via a conditional maximum likelihood approach (see Supplementary Note 2). The results of the exponential fits are shown in blue in Fig. 4, the result of the generalized Pareto fit is shown in Fig. 4b using a brown dashed line. Note that the parameter values obtained for Fig. 4b are in line with the direct measurement of the detector response shown in Supplementary Fig. 1: \(\hat{\gamma }/{\hat{\lambda }}_{b}/{\hat{i}}_{\max }=0.54\) versus 0.62 in the direct measurement.

As an interesting note, we mention that the generalized Pareto distribution (EEPF \(\propto {\left(1+\xi x\right)}^{-1/\xi }\)) includes the regular Pareto distribution (ξ > 0), the exponential distribution (ξ = 0), and the distribution derived for the observations beyond M* (ξ < 0) as well, so it should be possible to introduce a decreasing ξ(x) function to treat the three types of behavior at the same time. Moreover, in principle, one could include these aspects in the modeling approach of estimating the tail exponent as well; however, as the tail exponent has only little effect on the few observations beyond M, doing so would not likely improve the tail exponent estimation. On the contrary, introducing the extra parameters would negatively affect the stability of the numerical optimization.

Discussion

Optical rogue waves present an exciting direction of research and provide excellent means to study extreme statistical behavior in a controllable and reproducible fashion. In this study, we analyzed intensity data gathered from supercontinuum generation experiments fed by thermal light and bright squeezed vacuum. Even though optical experiments provide large amounts of data, they are highly affected by noise, pump depletion, and detector saturation. As a result, the effective sample size (observations that are not or are little affected by either issue) is much smaller than the total sample size, which makes the estimation problem non-trivial.

The rogueness of the observed intensity distributions comes from the fact that they display a power-law decay. We used two different, advanced methods to estimate the related exponent. Accurately estimating the rate of power-law decay is of both theoretical and practical importance. Knowing whether the theoretical distribution (unaffected by saturation issues) has a finite second moment or not determines whether, for example, calculating the correlation function g(2) is meaningful, and having a proper estimate of the tail exponent also helps with designing further experiments.

The first method estimates the value of the tail exponent directly and is the generalization of the well-known Hill estimator. As pump depletion and detector saturation have an effect on the largest values only, the estimation of the tail is much more precise if we discard these affected observations. This requires a modification of the Hill estimator but is otherwise quite straightforward. The second approach consists of devising a simplified physical model of the process (including noises and further limitations), and performing a maximum likelihood fit of its parameters based on the data. This approach is, of course, tailored to the specific problem at hand, and in a different context, requires setting up a different model. The largest values are discarded similarly to the first approach, which means that instead of having to add extra parameters to the model to describe pump depletion and the saturation curve of the detector, we only need to choose a limit beyond which values are discarded. Since the fit is quite good, this means we not only accurately estimated the parameters (including the tail exponent), but we also have a reasonably good grasp of the imperfections in the system. Using the two approaches in parallel is useful as well since they produce independent estimates. Consistent values indicate that our view of the process, and our implementation of the estimators are appropriate.

This dual approach is especially useful in the case of pumping with bright squeezed vacuum. We have a fundamental problem in both our estimation schemes: the direct method is better suited for an underlying exponential distribution than for gamma, while the modeling approach has problems with the fit as the physical process is more complex. Nevertheless, either method provides similar tail exponents, meaning that albeit the estimation procedures are more sensitive in the BSV case, we can still perform a consistent tail estimation.

Other than estimating the exponent of the power-law decay, we also showed how power-law behavior breaks down for the largest observations. The primary cause of this is pump depletion, turning the power-law decay into exponential. Furthermore, especially in the case of pumping with bright squeezed vacuum, high intensities beyond the detector’s linear response range were achieved, which additionally distorted the empirical distribution. We were able to provide a model to characterize this post-power-law range of observations through an exponential and a generalized Pareto distribution.

In summary, we have extensively addressed the problem of accurately describing rogue waves. In contrast to most publications related to rogue waves, we did not attempt to introduce a microscopic model to explain why our system produces extreme behavior. Instead, we applied a top-down approach: we used advanced statistical analysis of the available data, and from that, we obtained a quantitative description of the extreme behavior that also takes into account different physical imperfections of the system. Through investigating the particular case of supercontinuum generation, we provided a practical toolkit to analyze similar highly volatile processes that result in rogue waves.

Methods

Experiment

In the experiment (Fig. 1), the radiation of a titanium-sapphire laser is frequency doubled to generate pulses at 400 nm with a 1.4 ps pulse duration and up to 200 μJ of energy per pulse. This 400 nm radiation is used to pump two cascaded 3 mm BBO crystals in a type-I collinear parametric down-conversion (PDC) scheme. Depending on the crystal orientation, we can implement two processes54: (i) degenerate PDC, for which the signal and idler radiations have the same central wavelength (800 nm), (ii) non-degenerate PDC, for which the signal and idler radiations have different central wavelengths (signal 710 nm, idler 916 nm). To stress the different intensity statistics of these two types of light, in the following, we will call the signal radiation of the non-degenerate PDC at 710 nm thermal light and the result of the degenerate PDC at 800 nm bright squeezed vacuum (BSV). The radiation of non-degenerate PDC has intensity fluctuations identical to those of thermal light, larger than laser light55,56. The radiation of degenerate PDC (BSV) has even stronger intensity fluctuations46. The energy per pulse for BSV and thermal light was a few tens of nJ. These two light sources were filtered by bandpass filters: (i) at 710 ± 5 nm for thermal light, (ii) at 800 ± 5 nm for BSV, and were subsequently used to pump a 5 m single-mode fiber (SMF) with Ge-doped silica core (Thorlabs P3-780A-FC-5 patch cable with 780HP fiber) to generate a supercontinuum centered at 710 nm for thermal light pumping, and at 800 nm for BSV pumping. The fiber had normal dispersion in the studied range of wavelengths (from 700 –900 nm)57, and a nonlinear refractive index n2 around 3 × 10−20 m2/W58,59.

At the output of the fiber, the supercontinuum was spectrally filtered by a monochromator with 1 nm resolution and measured by a photodetector (PD) to reduce the averaging of statistics by the detector over different wavelengths. The filtering was performed at the extreme red part of the supercontinuum (830 nm) for thermal light and the extreme blue part of the supercontinuum (760 nm) for BSV. The photodetector was calibrated to convert its output voltage signal into the number of photons per pulse, which is the data used in our analysis. The upper limit to the detector’s linear response was ~106 photons per pulse, with a maximum output ~2 ⋅ 106 photons per pulse. Note that in some measurements, the data were post-selected to avoid pump intensity fluctuations in the right polarization for PDC generation. This means that the laser power was monitored continuously, and data corresponding to the power falling outside a certain window were discarded. In other cases, no post-selection was done in order to be able to check for temporal correlations. In either case, data was collected until the sample size of 105 was reached. Importantly, the decrease in pump power fluctuations did not have a large effect on the distribution of measured intensities, and, therefore, the applicability of our approach.

Rogue wave generation

In optical fibers, rogue waves are typically associated with solitons appearing under anomalous dispersion. However, the measurements by Manceau et al.46 (and also by Hammani et al.60 in a somewhat different regime) were done at wavelengths in the normal-dispersion regime. Moreover, the nonlinear refractive index of the fiber was also relatively low. Therefore, the appearance of very high-magnitude events was unexpected. The explanation, however, is simple: the super-Poissonian statistics of the pumping PDC light played the dominant role in the appearance of rogue waves under these conditions. In other words, the amplification effect is much more prominent if the pumping light is already highly fluctuating (compared to coherent pumping).

As a simple demonstration of rogue behavior, let us look at Fig. 5a, which shows a typical outcome of an experiment. The yellow points correspond to the top 1% of observations, the blue points to the bottom 99%. The histogram of the lower 99% is shown in Fig. 5b. From the histogram, one might mistakenly conclude that the interesting part of the distribution ends at about 5 × 103 photons per pulse. For example, for an exponential sample of 105 observations, the expectancy of the sample maximum is only about 2.6 times larger than the 99th percentile. In contrast, for the particular measurement depicted in Fig. 5, many observations are above this value, and the actual maximal value is about 41 times larger than the 99th percentile (i.e., an order higher than expected). This is the behavior that distinguishes these rogue waves from quieter processes, for which not much of interest happens regarding the largest observations. If one takes a look at the traditional criterion, namely an event whose magnitude exceeds twice the significant wave height, about 2% of observations in the sample shown in Fig. 5 are rogue.

Fig. 5: Sample time series.
figure 5

a Sample time series of the number of photons per pulse observed in an experiment. Time is shown in the number of observations; the sampling frequency was 5 kHz. The bottom 99% of photon number observations are colored blue, and the top 1% are colored yellow. b Histogram based on the blue dots in (a).

Full size image

Regarding the origin of rogue waves, the spectral broadening in the regime of normal group velocity dispersion with picosecond pulsing is usually explained by the combination of self- and cross-phase modulation (SPM and XPM) together with the four-wave-mixing (FWM) processes61. Similar to Takushima et al.62, our spectral broadening is symmetrical with respect to pump wavelength, see Fig. 6 (see also Manceau et al.46, Fig. 4 depicting similar spectra), which suggests that the stimulated Raman scattering should not dominate in our case.

Fig. 6: Typical single-pulse spectra of the generated supercontinuum.
figure 6

The violet, blue, yellow, orange, and red lines correspond to output spectra at a BSV pumping power of about 50 nJ; the BSV pump spectrum is shown in green. The supercontinuum spectra are symmetric with respect to pump wavelength and demonstrate high fluctuations at both edges.

Full size image

We are observing rogue waves well-detuned from the pump frequency; therefore, we can use four-wave mixing to explain the amplification effect. For normal group velocity dispersion, the main question is whether it is possible to get for our detuning Ω a positive parametric gain G and the corresponding \({\sinh }^{2}G\) power dependence, respectively. Indeed, following the works of Stolen63 and Wang64, the parametric gain is equal to

$$G=\sqrt{{\left(\frac{2\pi {n}_{2}{P}_{{{{{{{{\rm{p}}}}}}}}}}{{\lambda }_{{{{{{{{\rm{p}}}}}}}}}{A}_{{{{{{{{\rm{eff}}}}}}}}}}\right)}^{2}-{\left(\frac{{\beta }_{2}{\Omega }^{2}}{2}\right)}^{2}}\times {L}_{{{{{{{{\rm{coh}}}}}}}}},$$
(2)

where Pp and λp are the pumping peak power and wavelength, Aeff and β2 are effective mode area and group velocity dispersion of the fiber, Lcoh = 2π/∣β2Ω2∣ is the coherence length of the interaction. Taking into account the parameters of our fiber at λp = 800 nm, β2 = 40 fs2/mm and Aeff = 20 μm2, for the observation of FWM from BSV at 760 nm (Fig. 2b), we obtain a positive gain for BSV energy per pulse >33 nJ. It is somewhat smaller than the mean energy used for Fig. 2b (40 nJ), for which we are getting G around 2.1, taking into account Lcoh = 1.1 cm. However, the gain is much larger for more energetic pulses from the fluctuating BSV pump. Note that these estimates do not take into account the shift of the amplification band, which happens due to SPM and XPM.

In agreement with this estimate, the experiment demonstrates an exponential dependence of the output number of photons on the input pulse energy. Figure 7 shows the mean number of photons generated at 780 nm (blue points) as a function of the pulse energy of BSV pumping at 800 nm fitted by \({\sinh }^{2}(C\times {P}_{{{{{{{{\rm{p}}}}}}}}})\) function (red curve), where C is a constant. The estimate of parametric gain using Eq. (2) in this case gives a positive gain for BSV pump energies of >8 nJ per pulse, which is where we start observing some converted photons. The fit gives us the gain G = 3.4, which is close to the number estimated from Eq. (2).

Fig. 7: Exponential input-output relation.
figure 7

Number of photons at 780 nm as a function of BSV pump energy per pulse (blue points) together with the corresponding fit (red curve).

Full size image

Direct estimation of the tail exponent

In the supercontinuum intensity data to be analyzed, power-law behavior has both a lower and an upper limit. This upper limit is not considered in the statistical literature of tail exponent estimation because, in the usual contexts, it is much harder to attain. For example, as there is a finite amount of water on Earth, flood sizes are, of course, limited; however, no recorded flood size has ever come close to that limit. In our case, an upper limit exists because the values of the largest observations are affected by detector saturation and pump depletion. In other words, even though the observed data is strictly speaking not heavy-tailed, we posit that this is due only to experimental limitations and would like to minimize their effect on exponent estimates.

We refer to the first estimation approach as direct because it estimates the value of the tail exponent directly, supposing that there is a finite interval within the range of observed values in which the density of the intensity observations shows a power-law decay. The advantages of this approach are that it is straightforward and it is also more generally applicable than the current context of supercontinuum generation (it only assumes that there is an interval where the exceedance probability function decays at a power-law rate). However, it does not take into account deviations from exact power-law behavior (e.g., which might cause some bias for BSV source); nevertheless, it is an easy-to-implement tool that, in our case, has only little bias.

The standard option for directly estimating the value of the tail exponent is the Hill estimator34, defined as

$${\hat{\alpha }}_{{{{{{{{\rm{H}}}}}}}}}^{-1}(k)=\frac{1}{k}\mathop{\sum }\limits_{i=1}^{k}\ln {x}_{(i)}-\ln {x}_{(k+1)},$$
(3)

with x(i) denoting the ith largest element of the sample. Note that this formula is based on the k + 1 largest observations. However, since we have data that clearly do not decay at a power-law rate for large values, this method provides unreliable results (see Fig. 2, red line). Even if the tail of the distribution decays asymptotically at a power-law rate, for finite samples, the problem of choosing k is non-trivial and has an extensive literature65,66,67,68. The basic approach is visual and is referred to as the Hill plot: one has to look for a range of values of k where \({\hat{\alpha }}_{{{{{{{{\rm{H}}}}}}}}}^{-1}(k)\) is flat, that is, it is insensitive to the choice of k. Note that choosing the tail length is equivalent to choosing a lower limit m beyond which observations are taken into account. That is, the tail length k can be expressed as \(k(m)=\max \{i:{x}_{(i)} \, > \, m\}\). We prefer plotting the parameter estimate as a function of the limit m because it makes for an easy comparison of different estimators (see Fig. 3a).

In our previous work50, we proposed a generalization of (3) for distributions for which power-law behavior has both a lower limit m and a finite upper limit M. With \(k=\max \{i:{x}_{(i)} > m\}\) and \(j=\max \{i:{x}_{(i)} \, > \, M\}\), this generalized Hill estimator can be given as

$${\hat{\alpha }}_{{{{{{{{\rm{gH}}}}}}}}}^{-1}(k,j)= \,\frac{j}{k-j}(\ln {x}_{(j+1)}-\ln {x}_{(k+1)})\\ +\frac{1}{k-j}\mathop{\sum }\limits_{i=j+1}^{k}(\ln {x}_{(i)}-\ln {x}_{(k+1)}).$$
(4)

That is, out of the top k + 1 observations, one discards the j largest elements, and uses the remaining k + 1 − j observations to estimate the tail exponent; note that \({\hat{\alpha }}_{{{{{{{{\rm{H}}}}}}}}}^{-1}(k)\equiv {\hat{\alpha }}_{{{{{{{{\rm{gH}}}}}}}}}^{-1}(k,0)\).

Clearly, with no prior information on m and M, choosing their values based on the sample only is more involved than choosing the lower limit for the Hill estimator. We adapted an approach similar to the Hill plot, namely looking for an area where \({\hat{\alpha }}_{{{{{{{{\rm{gH}}}}}}}}}\) is not sensitive to the choice of [m, M]. This can, for example, be done by plotting the value of \({\hat{\alpha }}_{{{{{{{{\rm{gH}}}}}}}}}\) for several fixed values of M as a function of m. The likely ranges for the limits can be pinpointed by looking at the EEPF on a log-log scale. This visual approach is, of course, not feasible if one has a large number of samples to evaluate, but can be automated, for example, similarly to the heuristic algorithm proposed by Neves et al.69.

Tail exponent estimation as part of a model fit

The second approach, which we will refer to as the modeling approach, consists of fitting a multi-parameter model to the whole process, where the tail exponent is only one parameter out of a few.

As opposed to simulating the evolution of the non-linear Schrödinger equation, we take an opposite approach: we treat the process as a black box and fit a physically motivated functional form to the empirical distribution obtained from the measured data. This simplest model is based on four-wave mixing46, which we think is at the root of the amplification effect during the process. Due to the simplicity of the model, we can obtain a semi-analytic goodness of fit function, which helps with the stability and accuracy of the fit. Even though, similarly to the previously discussed direct approach, this procedure still takes a birds-eye view of the process, it also quantifies major experimental limitations. The model is the following:

$${I}_{{{{{{{{\rm{OUT}}}}}}}}}=R\left[K\cdot {\sinh }^{2}\left({I}_{{{{{{{{\rm{IN}}}}}}}}}+{\omega }_{1}\right)\right]+{\omega }_{2},$$
(5)

with

  • IOUT denoting the measured intensity at the end of the fiber;

  • IIN standing for the incoming intensity with a constant mean μ (further details on incoming light statistics are in Supplementary Note 3), which is

    • exponentially distributed for thermal(PDF \(\propto \exp \{-x/\mu \}\)),

    • gamma-distributed for a BSV source(PDF \(\propto {x}^{-1/2}\exp \left\{-x/2\mu \right\}\));

  • K: constant factor related to choosing the unit;

  • \({\omega }_{i} \sim {{{{{{{\mathcal{N}}}}}}}}\left(0,{\sigma }_{i}^{2}\right)\): independent Gaussian noises;

  • R( ⋅ ): detector response function.

The noise ω1 corresponds to additive noises that affect the incoming intensity even before the light enters the fiber (due to the \({\sinh }^{2}(\cdot )\) transformation, this is essentially a multiplicative noise), whereas ω2 is an additive detection noise. In order to avoid introducing extra parameters for the response function, we did not fit the model to the observations affected by detector saturation. This amounted to only taking into account the non-linearity of detector response about the noise floor l, through \(R(x)=\max \left\{l,x\right\}\), and discarding the largest observations.

In order to have a better understanding of how the individual parameters affect the output intensity distribution, let us look at the asymptotic exceedance probability for the thermal case in the absence of detection noise (σ2 = 0)50:

$${{{{{{{\bf{P}}}}}}}}\left({I}_{{{{{{{{\rm{OUT}}}}}}}}} > x\right)= \,{\left[{e}^{-\frac{{\sigma }_{1}^{2}}{\mu }}\cdot \frac{4x}{K}\right]}^{-\frac{1}{2\mu }}\\ \times \left[1-\frac{K}{4x\mu }+{{{{{{{\mathcal{O}}}}}}}}\left({x}^{-2}\right)\right].$$

This shows that the decay exponent is solely determined by the mean input intensity, whereas \({x}_{0}=K\cdot {e}^{{\sigma }_{1}^{2}/\mu }/4\) is a scaling factor.

This model can, of course, be further refined, but we were interested in the simplest version able to describe the observed process. This simplest version has five parameters: ϑ = (μ, l, K, σ1, σ2). The tail exponent of the output of this model is α = (2μ)−1 for the thermal, and α = (4μ)−1 for the BSV case.

The advantage of the model defined by (5) is that its density and distribution functions can be calculated semi-analytically. This gives us the opportunity to relatively easily perform a conditional (only observations below a pre-specified limit M are taken into account) maximum likelihood fit of its parameters. After the parameters are estimated, a simple binomial test can be performed to determine whether the fit should be rejected or not (further details of the method are discussed in Supplementary Note 1).