Abstract
Chemical graph theory, a subfield of graph theory, is used to investigate chemical substances and their characteristics. Chemical graph analysis sheds light on the connection, symmetry, and reactivity of molecules. It supports chemical property prediction, research of molecular reactions, drug development, and understanding of molecular networks. A crucial part of computational chemistry is chemical graph theory, which helps researchers analyze and manipulate chemical structures using graph algorithms and mathematical models. Beryllonitrene , a compound of interest due to its potential applications in various fields, is examined through the lens of graph theory and mathematical modeling. The study involves the calculation and interpretation of topological indices and graph entropy measures, which provide valuable insights into the structural and energetic properties of Beryllonitrene’s molecular graph. Logarithmic regression models are employed to establish correlations between these indices, entropy, and other relevant molecular attributes. The results contribute to a deeper understanding of Beryllonitrene’s complex characteristics, facilitating its potential applications in diverse scientific and technological domains. In this study, degree-based topological indices \(\text{TI}\) are determined, as well as the entropy of graphs based on these \(\text{TI}\).
Similar content being viewed by others
Introduction
Graph theory is a subfield of mathematics concerned with the study of graphs. A graph is a mathematical structure composed of a collection of objects known as vertices or nodes and a set of connections between these items known as edges. Relationships between distinct items are shown and analyzed using graphs1. The vertices of a graph represent items like cities, individuals, or molecules, while the edges reflect the connections or interactions between these entities. Edges can be directed (for a one-way connection) or undirected (for a two-way connection)2. Weights can also be added to graph edges to signify the strength or expense of the connections. the totla number of edges incident to a vertex is called the degree of that vertex and denoted by \(\S (\tau )\)3.
Graph theory provides a strong foundation for modeling and understanding complex systems and relationships. It provides tools and approaches for solving problems involving connectivity, optimization, and structure in graphs, and it has a wide range of real-world applications4. Topological indices are mathematical descriptors that analyze a molecule’s molecular graph to determine its connectivity and structural characteristics5. On the other hand, a compound’s physicochemical qualities are its physical and chemical characteristics that control how it behaves and interacts with other systems6. The connection between topological indices and a molecule’s physicochemical characteristics is supported by the idea that molecular structure affects molecular properties. Different topological indices capture distinct molecular structure components, which may affect or correlate with different physical properties7.
Topological indices such as the Wiener, Randic, and Zagreb indices reflect a molecule’s size or shape8,9. Higher values of these indices generally indicate larger or more complicated molecules, which can be related to qualities such as molecular weight, boiling temperature, or viscosity10,11. The topological polar surface area (TPSA) index measures the polar surface area of a molecule. Because of greater polarity, hydrogen bonding capacity, and interactions with solvent molecules, compounds with higher TPSA tend to have higher water solubility12. The logarithm of the octanol-water partition coefficient (logP) is a standard indicator of a compound’s lipophilicity or hydrophobicity. Some topological indices, such as the Balaban index and the connection index, have been discovered to correlate with logP values, implying a link between molecular structure and hydrophobic characteristics13.
Topological indices can reveal information about a molecule’s chemical reactivity. The Szeged index, for example, or the edge-connectivity index, can be used to predict a compound’s stability or reactivity. Liu et al.14,15 analyses of some structural properties of networks. Higher values of these indices may imply stronger chemical stability or resistance16. While topological indices can provide useful information about molecular structure and potential correlations with physicochemical features, they can not capture the full complexity of intermolecular interactions17,18. Nadeem et al.19 discussed the topological aspects of metal-organic structures. Ahmad et al.20,21 analysis the theoretical study of energy of phenylene and anthracene. Koam et.al22 computed the valency-based topological descriptor for Hexagon Star Networks. Liu et al.23,24 compute Hosoya index of some graphs based on connection number.They cannot predict all aspects of compound behavior. Other elements that influence physicochemical qualities include electronic structure, stereochemistry, and intermolecular forces25. As a result, a thorough understanding of compound properties frequently necessitates the consideration of many elements in addition to topological indices. Some Topological index are given in Table 1.
Topological indices for beryllonitrene \(BeN_4\)
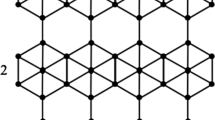
The structural organization of the chemical beryllonitrene is distinctive and fascinating. It is made up of a covalently linked network of beryllium (Be) and nitrogen (N) atoms. In a typical beryllonitrene molecule, four nitrogen atoms are connected to each beryllium atom, which forms the core of a tetrahedral coordination35. A crystal lattice or molecular network that resembles a three-dimensional honeycomb pattern is produced as a result of this arrangement shown in Fig. 1. Beryllonitrene has unique electrical and mechanical properties due to the alternation of beryllium and nitrogen atoms. Because of its extraordinary stability and electrical conductivity capabilities, beryllonitrene is of interest in a variety of sectors, including materials science and electronics. This is because beryllium, which is lightweight, forms strong covalent bonds with nitrogen36.
Beryllonitrene \(BeN_4\) sheet with unit cell35.
Let \(\text{G}=BeN_4\) be the molecular graph of Beryllonitrene having \(5mn+m+n+1\) number of vertices and \(8mn-n\) number of edges. The vertex division of the molecular graph is given in Table 2, while the edge division is given in Table 3.
-
General randic index
For \(\alpha =1\)
$$\begin{aligned} \text{R}_{1}\text {(BeN} _{4} ) &=(2)(1\times 2)+(2)(1\times 3)+(2n-2)(2\times 2)+(4m+4n-6)(2\times 3)\\&\quad +(4mn-3n)(3\times 3)+(4mn-4m-4n+4)(3\times 4)\\&=(2)(2)+(2)(3)+(2n-2)(4)+(4m+4n-6)(6)+(4mn-3n)(9)\\&\quad +(4mn-4m-4n+4)(12)\\&=84mn-24m-52n+14 \end{aligned}$$For \(\alpha =-1\)
$$\begin{aligned} \text{R}_{-1}\text {(BeN} _{4} ) &=(2)\left( \frac{1}{1\times 2} \right) +(2)\left( \frac{1}{1\times 3}\right) +(2n-2)\left( \frac{1}{2\times 2}\right) +(4m+4n-6)\left( \frac{1}{2\times 3}\right) \\&\quad +(4mn-3n)\left( \frac{1}{3\times 3}\right) +(4mn-4m-4n+4)\left( \frac{1}{3\times 4}\right) \\&=(2)\left( \frac{1}{2}\right) +(2)\left( \frac{1}{3}\right) +(2n-2)\left( \frac{1}{4}\right) +(4m+4n-6)\left( \frac{1}{6}\right) \\&\quad +(4mn-3n)\left( \frac{1}{9}\right) +(4mn-4m-4n+4)\left( \frac{1}{12}\right) \\&=0.7778mn+0.3333m+0.3889n+0.5 \end{aligned}$$For \(\alpha =\frac{1}{2}\)
$$\begin{aligned} \text{R}_{\frac{1}{2}}\text {(BeN} _{4} ) &=(2)(\sqrt{1\times 2})+(2)(\sqrt{1\times 3})+(2n-2)(\sqrt{2\times 2})+(4m+4n-6)(\sqrt{2\times 3})\\&\quad +(4mn-3n)(\sqrt{3\times 3})+(4mn-4m-4n+4)(\sqrt{3\times 4})\\&=(2)(\sqrt{2})+(2)(\sqrt{3})+(2n-2)(\sqrt{4})+(4m+4n-6)(\sqrt{6})\\&\quad +(4mn-3n)(\sqrt{9})+(4mn-4m-4n+4)(\sqrt{12})\\&=25.8564mn-4.0584m-12.0584n+1.4519 \end{aligned}$$For \(\alpha =-\frac{1}{2}\)
$$\begin{aligned} \text{R}_{-\frac{1}{2}}\text {(BeN} _{4} ) &=(2)\left( \frac{1}{\sqrt{1\times 2}}\right) +(2)\left( \frac{1}{\sqrt{1\times 3}}\right) +(2n-2)\left( \frac{1}{\sqrt{2\times 2}}\right) +(4m+4n-6)\left( \frac{1}{\sqrt{2\times 3}}\right) \\&\quad +(4mn-3n)\left( \frac{1}{\sqrt{3\times 3}}\right) +(4mn-4m-4n+4)\left( \frac{1}{\sqrt{3\times 4}}\right) \\&=(2)\left( \frac{1}{\sqrt{2}}\right) +(2)\left( \frac{1}{\sqrt{3}}\right) +(2n-2)\left( \frac{1}{\sqrt{4}}\right) +(4m+4n-6)\left( \frac{1}{\sqrt{6}}\right) \\&\quad +(4mn-3n)\left( \frac{1}{\sqrt{9}}\right) +(4mn-4m-4n+4)\left( \frac{1}{\sqrt{12}}\right) \\&=2.4880mn+0.4783m+0.1449n+0.2741 \end{aligned}$$The numerical and graphical representation of \(\text{R}_{1}\text {(BeN} _{4} ) \), \( {\text{R}}_{{ - 1}} ({\text{BeN}}_{4} ) \), \(\text{R}_{\frac{1}{2}}\text {(BeN} _{4} ) \) and \(\text{R}_{-\frac{1}{2}}\text {(BeN} _{4} ) \) is shown in Table 4 and Fig. 2, respectively.
Table 4 The numerical representation of \(\text{R}_{1}\text {(BeN} _{4} ) \), \(\text{R}_{-1}\text {(BeN} _{4} ) \), \(\text{R}_{\frac{1}{2}}\text {(BeN} _{4} ) \) and \(\text{R}_{-\frac{1}{2}}\text {(BeN} _{4} ) \). -
Atom bond connectivity index
$$\begin{aligned} {\text{ABC}}({\text{BeN}}_{4} ) &=(2)\left( \sqrt{\frac{1+2-2}{1\times 2}}\right) +(2)\left( \sqrt{\frac{1+3-2}{1\times 3}}\right) +(2n-2)\left( \sqrt{\frac{2+2-2}{2\times 2}}\right) +(4m+4n-6)\left( \sqrt{\frac{2+3-2}{2\times 3}}\right) \\&\quad +(4mn-3n)\left( \sqrt{\frac{3+3-2}{3\times 3}}\right) +(4mn-4m-4n+4)\left( \sqrt{\frac{3+4-2}{3\times 4}}\right) \\&=(2)\left( \sqrt{\frac{1}{2}}\right) +(2)\left( \sqrt{\frac{2}{3}}\right) +(2n-2)\left( \sqrt{\frac{2}{4}}\right) +(4m+4n-6)\left( \sqrt{\frac{3}{6}}\right) \\&\quad +(4mn-3n)\left( \sqrt{\frac{4}{9}}\right) +(4mn-4m-4n+4)\left( \sqrt{\frac{5}{12}}\right) \\&=5.2486mn+0.2464m-1.0060n-0.0276 \end{aligned}$$ -
Geometric arithmetic index
$$\begin{aligned} {\text{GA}}({\text{BeN}}_{4} ) &=(2)\left( \frac{2\sqrt{1\times 2}}{1+2}\right) +(2)\left( \frac{2\sqrt{1\times 3}}{1+3}\right) +(2n-2)\left( \frac{2\sqrt{2\times 2}}{2+2}\right) +(4m+4n-6)\left( \frac{2\sqrt{2\times 3}}{2+3}\right) \\&\quad +(4mn-3n)\left( \frac{2\sqrt{3\times 3}}{3+3}\right) +(4mn-4m-4n+4)\left( \frac{2\sqrt{3\times 4}}{3+4}\right) \\&=(2)\left( \frac{2\sqrt{2}}{3}\right) +(2)\left( \frac{2\sqrt{3}}{4}\right) +(2n-2)\left( \frac{2\sqrt{4}}{4}\right) +(4m+4n-6)\left( \frac{2\sqrt{6}}{5}\right) \\&\quad +(4mn-3n)\left( \frac{2\sqrt{9}}{6}\right) +(4mn-4m-4n+4)\left( \frac{2\sqrt{12}}{7}\right) \\&=7.9589mn-0.0793m-2.0397n-0.3021 \end{aligned}$$ -
First zagreb index
$$\begin{aligned} {\text{M}}_{1} ({\text{BeN}}_{4} ) &=(2)(1+2)+(2)(1+3)+(2n-2)(2+2)+(4m+4n-6)(2+3)\\&\quad +(4mn-3n)(3+3)+(4mn-4m-4n+4)(3+4)\\&=(2)(3)+(2)(4)+(2n-2)(4)+(4m+4n-6)(5)+(4mn-3n)(6)+(4mn-4m-4n+4)(7)\\&=52mn-8m-24n+4 \end{aligned}$$ -
Second zagreb index
$$\begin{aligned} {\text{M}}_{2} ({\text{BeN}}_{4} ) &=(2)(1\times 2)+(2)(1\times 3)+(2n-2)(2\times 2)+(4m+4n-6)(2\times 3)\\&\quad +(4mn-3n)(3\times 3)+(4mn-4m-4n+4)(3\times 4)\\&=(2)(2)+(2)(3)+(2n-2)(4)+(4m+4n-6)(6)+(4mn-3n)(9)+(4mn-4m-4n+4)(12)\\&=84mn-24m-52n+14 \end{aligned}$$The numerical and graphical representation of \( {\text{ABC}}({\text{BeN}}_{4} ) \), \( {\text{GA}}({\text{BeN}}_{4} ) \), \( {\text{M}}_{1} ({\text{BeN}}_{4} ) \) and \( {\text{M}}_{2} ({\text{BeN}}_{4} ) \) is shown in Table 5 and Fig. 3, respectively.
Table 5 The numerical representation of \( {\text{ABC}}({\text{BeN}}_{4} ) \), \( {\text{GA}}({\text{BeN}}_{4} ) \), \( {\text{M}}_{1} ({\text{BeN}}_{4} ) \) and \( {\text{M}}_{2} ({\text{BeN}}_{4} ) \). -
Harmonic zagreb index
$$\begin{aligned} {\text{HM}}({\text{BeN}}_{4} ) &=(2)(1+2)^2+(2)(1+3)^2+(2n-2)(2+2)^2+(4m+4n-6)(2+3)^2\\&\quad +(4mn-3n)(3+3)^2+(4mn-4m-4n+4)(3+4)^2\\&=(2)(3)^2+(2)(4)^2+(2n-2)(4)^2+(4m+4n-6)(5)^2+(4mn-3n)(6)^2+(4mn-4m-4n+4)(7)^2\\&=(2)(9)+(2)(16)+(2n-2)(16)+(4m+4n-6)(25)+(4mn-3n)(36)+(4mn-4m-4n+4)(49)\\&=340mn-96m-208n+64 \end{aligned}$$ -
Forgotton index
$$\begin{aligned} {\text{F}}({\text{BeN}}_{4} ) &=(2)(1^2+2^2)+(2)(1^2+3^2)+(2n-2)(2^2+2^2)+(4m+4n-6)(2^2+3^2)\\&\quad +(4mn-3n)(3^2+3^2)+(4mn-4m-4n+4)(3^2+4^2)\\&=(2)(1+4)+(2)(1+9)+(2n-2)(4+4)+(4m+4n-6)(4+9)+(4mn-3n)(9+9)\\&\quad +(4mn-4m-4n+4)(9+16)\\&=(2)(4)+(2)(10)+(2n-2)(8)+(4m+4n-6)(13)+(4mn-3n)(18)+(4mn-4m-4n+4)(25)\\&=172mn-48m-104n+36 \end{aligned}$$ -
Augmented zagreb index
$$\begin{aligned} {\text{AZI}}({\text{BeN}}_{4} ) &=(2)\left( \frac{1\times 2}{1+2-2}\right) ^3+(2)\left( \frac{1\times 3}{1+3-2}\right) ^3+(2n-2)\left( \frac{2\times 2}{2+2-2}\right) ^3+(4m+4n-6)\left( \frac{2\times 3}{2+3-2}\right) ^3\\&\quad +(4mn-3n)\left( \frac{3\times 3}{3+3-2}\right) ^3+(4mn-4m-4n+4)\left( \frac{3\times 4}{3+4-2}\right) ^3\\&=(2)(\frac{2}{1})+(2)\left( \frac{3}{2}\right) +(2n-2)\left( \frac{4}{2}\right) +(4m+4n-6)\left( \frac{6}{3}\right) \\&\quad +(4mn-3n)\left( \frac{9}{4}\right) +(4mn-4m-4n+4)\left( \frac{12}{5}\right) \\&=100.8585mn-23.2960m-52.8585n+14.0460 \end{aligned}$$ -
First redefined zagreb index
$$\begin{aligned} {\text{ReZG}}_{1} ({\text{BeN}}_{4} ) &=(2)(\frac{1+2}{1\times 2})+(2)(\frac{1+3}{1\times 3})+(2n-2)(\frac{2+2}{2\times 2})+(4m+4n-6)(\frac{2+3}{2\times 3})\\&\quad +(4mn-3n)(\frac{3+3}{3\times 3})+(4mn-4m-4n+4)(\frac{3+4}{3\times 4})\\&=(2)(\frac{3}{2})+(2)(\frac{4}{3})+(2n-2)(\frac{4}{4})+(4m+4n-6)(\frac{5}{6})\\&\quad +(4mn-3n)(\frac{6}{9})+(4mn-4m-4n+4)(\frac{7}{12})\\&=5mn+m+0.3333n+1 \end{aligned}$$The numerical and graphical representation of \( {\text{HM}}({\text{BeN}}_{4} ) \), \( {\text{F}}({\text{BeN}}_{4} ) \), \( {\text{AZI}}({\text{BeN}}_{4} ) \) and \( {\text{ReZG}}_{1} ({\text{BeN}}_{4} ) \) is shown in Table 6 and Fig. 4, respectively.
Table 6 The numerical representation of \( {\text{HM}}({\text{BeN}}_{4} ) \), \( {\text{F}}({\text{BeN}}_{4} ) \), \( {\text{AZI}}({\text{BeN}}_{4} ) \) and \( {\text{ReZG}}_{1} ({\text{BeN}}_{4} ) \). -
Second redefined zagreb index
$$\begin{aligned} {\text{ReZG}}_{2} ({\text{BeN}}_{4} ) &=(2)(\frac{1\times 2}{1+2})+(2)(\frac{1\times 3}{1+3})+(2n-2)(\frac{2\times 2}{2+2})+(4m+4n-6)(\frac{2\times 3}{2+3})\\&\quad +(4mn-3n)(\frac{3\times 3}{3+3})+(4mn-4m-4n+4)(\frac{3\times 4}{3+4})\\&=(2)(\frac{2}{3})+(2)(\frac{3}{4})+(2n-2)(\frac{4}{4})+(4m+4n-6)(\frac{6}{5})\\&\quad +(4mn-3n)(\frac{9}{6})+(4mn-4m-4n+4)(\frac{12}{7})\\&=12.8571mn-2.0571m-6.0571n+0.4905 \end{aligned}$$ -
Third redefined zagreb index
$$\begin{aligned} {\text{ReZG}}_{3} ({\text{BeN}}_{4} ) &=(2)((1+2)(1\times 2))+(2)((1+3)(1\times 3))+(2n-2)((2+2)(2\times 2))\\{} & {} +(4m+4n-6)((2+3)(2\times 3))\\{} & {} +(4mn-3n)((3+3)(3\times 3))+(4mn-4m-4n+4)((3+4)(3\times 4))\\{} & {} =(2)(3\times 2)+(2)(4\times 3)+(2n-2)(4\times 4)+(4m+4n-6)(5\times 6)\\{} & {} +(4mn-3n)(6\times 9)+(4mn-4m-4n+4)(7\times 12)\\{} & {} =(2)(6)+(2)(12)+(2n-2)(16)+(4m+4n-6)(30)\\{} & {} +(4mn-3n)(54)+(4mn-4m-4n+4)(84)\\{} & {} =544mn-208m-392n+152 \end{aligned}$$The numerical and graphical representation of \( {\text{ReZG}}_{2} ({\text{BeN}}_{4} ) \) and \( {\text{ReZG}}_{3} ({\text{BeN}}_{4} ) \) is shown in Table 7 and Fig. 5, respectively.
Table 7 The numerical representation of \( {\text{ReZG}}_{2} ({\text{BeN}}_{4} ) \) and \( {\text{ReZG}}_{3} ({\text{BeN}}_{4} ) \).
Graph entropy
Entropy is the measurement of disorders of a system while the measurement of unpredictability of information content or the measurement of uncertainty of a system also called the entropy of a system, the concept was introduce in 194837. The concept of graph entropy was applied in chemistry, biology, and other sciences38. There are different types of graphs for measuring entropy, for exploring the network the degree power is most significant.
where \(\varpi _{d}=\sum _{i=1}^{m}\Theta _{i}{I(\rho _{i}\varrho _{i})}\) is topological index \(\Theta _{i}\) is frequency m is number of edges \(I(\rho \varrho )\) is the weight of the edge \(\rho \varrho \) see37. By using Tables 1 and 3 and Eq. (1), we have following formulas and their calculation.
In chemistry and related sciences, topological indices are mathematical descriptors that describe the topology of molecular structures. In relation to these indices, entropy may be defined as the degree of randomness or disorder in the distribution of specific structural characteristics. The calculation of entropy using topological indices in the context of molecular structures can offer several benefits.
-
The structural diversity of molecular compounds can be quantitatively evaluated using entropy measures that are derived from topological indices. Greater structural diversity may be indicated by higher entropy values, which would add to a more varied chemical space.
-
Entropy measurements are correlated with a number of molecular properties, both chemical and physical. Properties like solubility, boiling points, and reaction rates can be predicted by using topological indices in entropy calculations.
-
Entropy makes it possible to compare various molecular sets or chemical databases according to the structural diversity of each set. Entropy values can be used by researchers to rank or screen compounds for additional testing.
-
Randic entropy
For \(\alpha =1\)
$$\begin{aligned} {\text{ENT}}_{{ {\text{R}}_{1} ({\text{BeN}}_{4} )}} &=\log (R_{1})-{\frac{1}{(R_{1})}}\sum _{i=1}^{6}\Theta {(\rho \times \varrho )}\log _{2}{(\rho \times \varrho )}\\&=\log (84mn-24m-52n+14)-\frac{(2)\log (2)^2}{84mn-24m-52n+14}-\frac{(2)\log (3)^3}{84mn-24m-52n+14}\\&\quad -\frac{(2n-2)\log (4)^4}{84mn-24m-52n+14}-\frac{(4m+4n-6)\log (6)^6}{84mn-24m-52n+14}-\frac{(4mn-3n)\log (9)^9}{84mn-24m-52n+14}\\&\quad -\frac{(4mn-4m-4n+4)\log (12)^{12}}{84mn-24m-52n+14}\\ \end{aligned}$$For \(\alpha =-1\)
$$\begin{aligned} {\text{ENT}}_{{{\text{R}}_{{ - 1}} ({\text{BeN}}_{4} )}} &=\log (R_{-1})-{\frac{1}{(R_{-1})}}\sum _{i=1}^{6}\Theta {\frac{1}{(\rho \times \varrho )}}\log _{2}{\frac{1}{(\rho \times \varrho )}}\\&=\log (0.7778mn+0.3333m+0.3889n+0.5)-\frac{(2)\log (\frac{1}{2})^{\frac{1}{2}}}{0.7778mn+0.3333m+0.3889n+0.5}\\&\quad -\frac{(2)\log (\frac{1}{3})^{\frac{1}{3}}}{0.7778mn+0.3333m+0.3889n+0.5}-\frac{(2n-2)\log (\frac{1}{4})^{\frac{1}{4}}}{0.7778mn+0.3333m+0.3889n+0.5}\\&\quad -\frac{(4m+4n-6)\log (\frac{1}{6})^{\frac{1}{6}}}{0.7778mn+0.3333m+0.3889n+0.5}-\frac{(4mn-3n)\log (\frac{1}{9})^{\frac{1}{9}}}{0.7778mn+0.3333m+0.3889n+0.5}\\&\quad -\frac{(4mn-4m-4n+4)\log (\frac{1}{12})^{\frac{1}{12}}}{0.7778mn+0.3333m+0.3889n+0.5}\\ \end{aligned}$$For \(\alpha =\frac{1}{2}\)
$$\begin{aligned} {\text{ENT}}_{{{\text{R}}_{{\frac{1}{2}}} ({\text{BeN}}_{4} )}} &=\log (R_{\frac{1}{2}})-{\frac{1}{(R_{\frac{1}{2}})}}\sum _{i=1}^{6}\Theta {\sqrt{(\rho \times \varrho )}}\log _{2}{\sqrt{(\rho \times \varrho )}}\\&=\log (25.8564mn-4.0584m-12.0584n+1.4519)-\frac{(2)\log (\sqrt{2})^{\sqrt{2}}}{25.8564mn-4.0584m-12.0584n+1.4519}\\&\quad -\frac{(2)\log (\sqrt{3})^{\sqrt{3}}}{25.8564mn-4.0584m-12.0584n+1.4519}-\frac{(2n-2)\log (\sqrt{4})^{\sqrt{4}}}{25.8564mn-4.0584m-12.0584n+1.4519}\\&\quad -\frac{(4m+4n-6)\log (\sqrt{6})^{\sqrt{6}}}{25.8564mn-4.0584m-12.0584n+1.4519}-\frac{(4mn-3n)\log (\sqrt{9})^{\sqrt{9}}}{25.8564mn-4.0584m-12.0584n+1.4519}\\&\quad -\frac{(4mn-4m-4n+4)\log (\sqrt{12})^{\sqrt{12}}}{25.8564mn-4.0584m-12.0584n+1.4519}\\ \end{aligned}$$For \(\alpha =\frac{1}{2}\)
$$\begin{aligned} {\text{ENT}}_{{{\text{R}}_{{ - \frac{1}{2}}} ({\text{BeN}}_{4} )}} &=\log (R_{-\frac{1}{2}})-{\frac{1}{(R_{-\frac{1}{2}})}}\sum _{i=1}^{6}\Theta {\frac{1}{\sqrt{(\rho \times \varrho )}}}\log _{2}{\frac{1}{\sqrt{(\rho \times \varrho )}}}\\&=\log (2.4880mn+0.4783m+0.1449n+0.2741)-\frac{(2)\log (\frac{1}{\sqrt{2}})^{\frac{1}{\sqrt{2}}}}{2.4880mn+0.4783m+0.1449n+0.2741}\\&\quad -\frac{(2)\log (\frac{1}{\sqrt{3}})^{\frac{1}{\sqrt{3}}}}{2.4880mn+0.4783m+0.1449n+0.2741}-\frac{(2n-2)\log (\frac{1}{\sqrt{4}})^{\frac{1}{\sqrt{4}}}}{2.4880mn+0.4783m+0.1449n+0.2741}\\&\quad -\frac{(4m+4n-6)\log (\frac{1}{\sqrt{6}})^{\frac{1}{\sqrt{6}}}}{2.4880mn+0.4783m+0.1449n+0.2741}-\frac{(4mn-3n)\log (\frac{1}{\sqrt{9}})^{\frac{1}{\sqrt{9}}}}{2.4880mn+0.4783m+0.1449n+0.2741}\\&\quad -\frac{(4mn-4m-4n+4)\log (\frac{1}{\sqrt{12}})^{\frac{1}{\sqrt{12}}}}{2.4880mn+0.4783m+0.1449n+0.2741}\\ \end{aligned}$$The numerical and graphical representation of \( {\text{ENT}}_{{ {\text{R}}_{1} ({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{R}}_{{ - 1}} ({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{R}}_{{\frac{1}{2}}} ({\text{BeN}}_{4} )}} \) and \( {\text{ENT}}_{{{\text{R}}_{{ - \frac{1}{2}}} ({\text{BeN}}_{4} )}} \) is shown in Table 8 and Fig. 6, respectively.
Table 8 The numerical representation of \( {\text{ENT}}_{{ {\text{R}}_{1} ({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{R}}_{{ - 1}} ({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{R}}_{{\frac{1}{2}}} ({\text{BeN}}_{4} )}} \) and \( {\text{ENT}}_{{{\text{R}}_{{ - \frac{1}{2}}} ({\text{BeN}}_{4} )}} \). Figure 6 The graphical representation of \( {\text{ENT}}_{{ {\text{R}}_{1} ({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{R}}_{{ - 1}} ({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{R}}_{{\frac{1}{2}}} ({\text{BeN}}_{4} )}} \) and \( {\text{ENT}}_{{{\text{R}}_{{ - \frac{1}{2}}} ({\text{BeN}}_{4} )}} \).
-
Atom bond connectivity entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{ABC}}({\text{BeN}}_{4} )}} &=\log (ABC)-{\frac{1}{(ABC)}}\sum _{i=1}^{6}\Theta {\sqrt{\frac{\rho +\varrho -2}{\rho \times \varrho }}}\log _{2}{\sqrt{\frac{\rho +\varrho -2}{\rho \times \varrho }}}\\ ENT_{ABC}&=\log (5.2486mn+0.2464m-1.0060n-0.0276)-\frac{(2)\log (\sqrt{\frac{1}{2}})^{\sqrt{\frac{1}{2}}}}{5.2486mn+0.2464m-1.0060n-0.0276}\\&\quad -\frac{(2)\log (\sqrt{\frac{2}{3}})^{\sqrt{\frac{2}{3}}}}{5.2486mn+0.2464m-1.0060n-0.0276}-\frac{(2n-2)\log (\sqrt{\frac{2}{4}})^{\sqrt{\frac{2}{4}}}}{5.2486mn+0.2464m-1.0060n-0.0276}\\&\quad -\frac{(4m+4n-6)\log (\sqrt{\frac{3}{6}})^{\sqrt{\frac{3}{6}}}}{5.2486mn+0.2464m-1.0060n-0.0276}-\frac{(4mn-3n)\log (\sqrt{\frac{4}{9}})^{\sqrt{\frac{4}{9}}}}{5.2486mn+0.2464m-1.0060n-0.0276}\\&\quad -\frac{(4mn-4m-4n+4)\log (\sqrt{\frac{5}{12}})^{\sqrt{\frac{5}{12}}}}{5.2486mn+0.2464m-1.0060n-0.0276}\\ \end{aligned}$$ -
Geometric arithmetic entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{GA}}({\text{BeN}}_{4} )}} &=\log (GA)-{\frac{1}{(GA)}}\sum _{i=1}^{6}\Theta {\frac{2\sqrt{\rho \times \varrho }}{\rho +\varrho }}\log _{2}{\frac{2\sqrt{\rho \times \varrho }}{\rho +\varrho }}\\&=\log (7.9589mn-0.0793m-2.0397n-0.3021)-\frac{(2)\log (\frac{2\sqrt{2}}{3})^{\frac{2\sqrt{2}}{3}}}{7.9589mn-0.0793m-2.0397n-0.3021}\\&\quad -\frac{(2)\log (\frac{2\sqrt{3}}{4})^{\frac{2\sqrt{3}}{4}}}{7.9589mn-0.0793m-2.0397n-0.3021}-\frac{(2n-2)\log (\frac{2\sqrt{4}}{4})^{\frac{2\sqrt{4}}{4}}}{7.9589mn-0.0793m-2.0397n-0.3021}\\&\quad -\frac{(4m+4n-6)\log (\frac{2\sqrt{6}}{5})^{\frac{2\sqrt{6}}{5}}}{7.9589mn-0.0793m-2.0397n-0.3021}-\frac{(4mn-3n)\log (\frac{2\sqrt{9}}{6})^{\frac{2\sqrt{9}}{6}}}{7.9589mn-0.0793m-2.0397n-0.3021}\\&\quad -\frac{(4mn-4m-4n+4)\log (\frac{2\sqrt{12}}{7})^{\frac{2\sqrt{12}}{7}}}{7.9589mn-0.0793m-2.0397n-0.3021}\\ \end{aligned}$$ -
First zagreb entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{M}}_{1} ({\text{BeN}}_{4} )}} &=\log (M_{1})-{\frac{1}{(M_{1})}}\sum _{i=1}^{6}\Theta {(\rho +\varrho )}\log _{2}{(\rho +\varrho )}\\&=\log (52mn-8m-24n+4)-\frac{(2)\log (3)^3}{52mn-8m-24n+4}-\frac{(2)\log (4)^4}{52mn-8m-24n+4}\\&\quad -\frac{(2n-2)\log (4)^4}{52mn-8m-24n+4}-\frac{(4m+4n-6)\log (5)^5}{52mn-8m-24n+4}-\frac{(4mn-3n)\log (6)^6}{52mn-8m-24n+4}\\&\quad -\frac{(4mn-4m-4n+4)\log (7)^7}{52mn-8m-24n+4}\\ \end{aligned}$$ -
Second zagreb entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{M}}_{2} ({\text{BeN}}_{4} )}}&=\log (M_{2})-{\frac{1}{(M_{2})}}\sum _{i=1}^{6}\Theta {(\rho \times \varrho )}\log _{2}{(\rho \times \varrho )}\\&=\log (84mn-24m-52n+14)-\frac{(2)\log (2)^2}{84mn-24m-52n+14}-\frac{(2)\log (3)^3}{84mn-24m-52n+14}\\&\quad -\frac{(2n-2)\log (4)^4}{84mn-24m-52n+14}-\frac{(4m+4n-6)\log (6)^6}{84mn-24m-52n+14}-\frac{(4mn-3n)\log (9)^9}{84mn-24m-52n+14}\\&\quad -\frac{(4mn-4m-4n+4)\log (12)^{12}}{84mn-24m-52n+14}\\ \end{aligned}$$The numerical and graphical representation of \( {\text{ENT}}_{{{\text{ABC}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{GA}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{M}}_{1} ({\text{BeN}}_{4} )}} \) and \({\text{ENT}}_{{{\text{M}}_{2} ({\text{BeN}}_{4} )}}\) is shown in Table 9 and Fig. 7, respectively.
Table 9 The numerical representation of \( {\text{ENT}}_{{{\text{ABC}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{GA}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{M}}_{1} ({\text{BeN}}_{4} )}} \) and \({\text{ENT}}_{{{\text{M}}_{2} ({\text{BeN}}_{4} )}}\). -
Harmonic zagreb entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{HM}}({\text{BeN}}_{4} )}} &=\log (HM)-{\frac{1}{(HM)}}\sum _{i=1}^{6}\Theta {(\rho +\varrho )^2}\log _{2}{(\rho +\varrho )^2}\\&=\log (340mn-96m-208n+64)-\frac{(2)\log (9)^9}{340mn-96m-208n+64}-\frac{(2)\log (16)^{16}}{340mn-96m-208n+64}\\&\quad -\frac{(2n-2)\log (16)^{16}}{340mn-96m-208n+64}-\frac{(4m+4n-6)\log (25)^{25}}{340mn-96m-208n+64}-\frac{(4mn-3n)\log (36)^36}{340mn-96m-208n+64}\\&\quad -\frac{(4mn-4m-4n+4)\log (49)^49}{340mn-96m-208n+64}\\ \end{aligned}$$ -
Forgotton entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{F}}({\text{BeN}}_{4} )}} &=\log (F)-{\frac{1}{(F)}}\sum _{i=1}^{6}\Theta {(\rho ^2+\varrho ^2)}\log _{2}{(\rho ^2+\varrho ^2)}\\&=\log (172mn-48m-104n+36)-\frac{(2)\log (4)^4}{172mn-48m-104n+36}-\frac{(2)\log (10)^{10}}{172mn-48m-104n+36}\\&\quad -\frac{(2n-2)\log (8)^8}{172mn-48m-104n+36}-\frac{(4m+4n-6)\log (13)^{13}}{172mn-48m-104n+36}-\frac{(4mn-3n)\log (18)^{18}}{172mn-48m-104n+36}\\&\quad -\frac{(4mn-4m-4n+4)\log (25)^{25}}{172mn-48m-104n+36}\\ \end{aligned}$$ -
Augmented zagreb entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{AZI}}({\text{BeN}}_{4} )}} &=\log (AZI)-{\frac{1}{(AZI)}}\sum _{i=1}^{6}\Theta {\left( \frac{\rho \times \varrho }{\rho +\varrho -2}\right) ^3}\log _{2}{\left( \frac{\rho \times \varrho }{\rho +\varrho -2}\right) ^3}\\&=\log (100.8585mn-23.2960m-52.8585n+14.0460)\\{} & {} -\frac{(2)\log ((\frac{2}{1})^3)^{(\frac{2}{1})^3}}{100.8585mn-23.2960m-52.8585n+14.0460}\\{} & {} -\frac{(2)\log ((\frac{3}{2})^3)^{(\frac{3}{2})^3}}{100.8585mn-23.2960m-52.8585n+14.0460}\\{} & {} -\frac{(2n-2)\log ((\frac{4}{2})^3)^{(\frac{4}{2})^3}}{100.8585mn-23.2960m-52.8585n+14.0460}\\{} & {} -\frac{(4m+4n-6)\log ((\frac{6}{3})^3)^{(\frac{6}{3})^3}}{100.8585mn-23.2960m-52.8585n+14.0460}\\{} & {} -\frac{(4mn-3n)\log ((\frac{9}{4})^3)^{(\frac{9}{4})^3}}{100.8585mn-23.2960m-52.8585n+14.0460}\\{} & {} -\frac{(4mn-4m-4n+4)\log ((\frac{12}{5})^3)^{(\frac{12}{5})^3}}{100.8585mn-23.2960m-52.8585n+14.0460}\\ \end{aligned}$$ -
First redefined zagreb entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{ReZG}}_{1} ({\text{BeN}}_{4} )}} &=\log (ReZG_1)-{\frac{1}{(ReZG_1)}}\sum _{i=1}^{6}\Theta {\left( \frac{\rho +\varrho }{\rho \times \varrho }\right) }\log _{2}{\left( \frac{\rho +\varrho }{\rho \times \varrho }\right) }\\ ReZG_1&=\log (5mn+m+0.3333n+1)-\frac{(2)\log (\frac{3}{2})^{\frac{3}{2}}}{5mn+m+0.3333n+1}\\{} & {} -\frac{(2)\log (\frac{4}{3})^{\frac{4}{3}}}{5mn+m+0.3333n+1}\\{} & {} -\frac{(2n-2)\log (\frac{4}{4})^{\frac{4}{4}}}{5mn+m+0.3333n+1}-\frac{(4m+4n-6)\log (\frac{5}{6})^{\frac{5}{6}}}{5mn+m+0.3333n+1}\\{} & {} -\frac{(4mn-3n)\log (\frac{6}{9})^{\frac{6}{9}}}{5mn+m+0.3333n+1}-\frac{(4mn-4m-4n+4)\log (\frac{7}{12})^{\frac{7}{12}}}{5mn+m+0.3333n+1}\\ \end{aligned}$$The numerical and graphical representation of \( {\text{ENT}}_{{{\text{HM}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{F}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{AZI}}({\text{BeN}}_{4} )}} \) and \( {\text{ENT}}_{{{\text{ReZG}}_{1} ({\text{BeN}}_{4} )}} \) is shown in Table 10 and Fig. 8, respectively.
Table 10 The numerical representation of \( {\text{ENT}}_{{{\text{HM}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{F}}({\text{BeN}}_{4} )}} \), \( {\text{ENT}}_{{{\text{AZI}}({\text{BeN}}_{4} )}} \) and \( {\text{ENT}}_{{{\text{ReZG}}_{1} ({\text{BeN}}_{4} )}} \). -
Second redefined zagreb entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{ReZG}}_{2} ({\text{BeN}}_{4} )}} &=\log (ReZG_2)-{\frac{1}{(ReZG_2)}}\sum _{i=1}^{6}\Theta {\left( \frac{\rho \times \varrho }{\rho +\varrho }\right) }\log _{2}{\left( \frac{\rho \times \varrho }{\rho +\varrho }\right) }\\&=\log (12.8571mn-2.0571m-6.0571n+0.4905)-\frac{(2)\log (\frac{2}{3})^{\frac{2}{3}}}{12.8571mn-2.0571m-6.0571n+0.4905}\\&\quad -\frac{(2)\log (\frac{3}{4})^{\frac{3}{4}}}{12.8571mn-2.0571m-6.0571n+0.4905}-\frac{(2n-2)\log (\frac{4}{4})^{\frac{4}{4}}}{12.8571mn-2.0571m-6.0571n+0.4905}\\&\quad -\frac{(4m+4n-6)\log (\frac{6}{5})^{\frac{6}{5}}}{12.8571mn-2.0571m-6.0571n+0.4905}-\frac{(4mn-3n)\log (\frac{9}{6})^{\frac{9}{6}}}{12.8571mn-2.0571m-6.0571n+0.4905}\\&\quad -\frac{(4mn-4m-4n+4)\log (\frac{12}{7})^{\frac{12}{7}}}{12.8571mn-2.0571m-6.0571n+0.4905}\\ \end{aligned}$$ -
Third redefined zagreb entropy
$$\begin{aligned} {\text{ENT}}_{{{\text{ReZG}}_{3} ({\text{BeN}}_{4} )}} &=\log (ReZG_3)-{\frac{1}{(ReZG_3)}}\sum _{i=1}^{6}\Theta {\left( ({\rho \times \varrho })({\rho +\varrho })\right) }\log _{2}{\left( ({\rho \times \varrho })({\rho +\varrho })\right) }\\&=\log (544mn-208m-392n+152)-\frac{(2)\log (6)^6}{544mn-208m-392n+152}-\frac{(2)\log (12)^{12}}{544mn-208m-392n+152}\\&\quad -\frac{(2n-2)\log (16)^{16}}{544mn-208m-392n+152}-\frac{(4m+4n-6)\log (30)^{30}}{544mn-208m-392n+152}-\frac{(4mn-3n)\log (54)^{54}}{544mn-208m-392n+152}\\&\quad -\frac{(4mn-4m-4n+4)\log (84)^{84}}{544mn-208m-392n+152}\\ \end{aligned}$$The numerical and graphical representation of \( {\text{ENT}}_{{{\text{ReZG}}_{2} ({\text{BeN}}_{4} )}} \), and \({\text{ENT}}_{{{\text{ReZG}}_{3} ({\text{BeN}}_{4} )}}\) is shown in Table 11 and Fig. 9, respectively.
Table 11 The numerical representation of \({\text{ENT}}_{{{\text{ReZG}}_{2} ({\text{BeN}}_{4} )}}\), and \({\text{ENT}}_{{{\text{ReZG}}_{3} ({\text{BeN}}_{4} )}}\).
Logarithmic regression model and its analysis
A dependent variable and one or more independent variables are modeled, and the connection between them is examined using the statistical approach known as regression analysis39. It is frequently used to comprehend the effects of independent factors on the dependent variable and create forecasts or estimates in various domains, including economics, finance, social sciences, and engineering40. Regression analysis’ fundamental premise is to identify the line or curve that best captures the connection between the variables. The variable you seek to predict or explain is the dependent variable, called the response variable. The variables expected to impact the dependent variable are referred to as independent variables, often known as predictor variables or explanatory variables41. We used the SPSS software for these analysis (https://www.ibm.com/products/spss-statistics). Regression analysis may have many different forms, but the most popular one is basic linear regression, which only requires one independent variable. The relationship between the variables is considered linear in basic linear regression42. The line’s equation is displayed as:
where, Y is the dependent variable, \(\beta _{0}\) is the Y-intercept, \(\beta _{i}\) is the Coefficients of independent variable for \(i=1...z\), X is the Independent variable and, \(\varepsilon \) is the Error.
To minimize the sum of squared differences between the observed values of Y and the anticipated values from the model, regression analysis aims to estimate the values of \(\beta _{0}\) and \(\beta _{1}\). The least squares method is commonly used for this estimating process. Regression analysis also offers several statistical measures to evaluate the model’s quality, such as the coefficient of determination \((R^2)\), which shows the percentage of the dependent variable’s variance that can be accounted for by the independent variables. Regression analysis is a potent tool for figuring out how variables relate to one another, formulating predictions, and investigating cause-and-effect relationships. It is widely used in many disciplines for data analysis, decision-making, and research43.
A statistical method for modeling the relationship between a dependent variable and one or more independent variables where a logarithmic scale may better represent the relationship is known as logarithmic regression analysis, logarithmic transformation, or log-linear regression44.
where, Y is the dependent variable, \(\beta _{0}\) is the Y-intercept, \(\beta _{i}\) is the Coefficients of independent variable for \(i=1 \ldots z\), X is the Independent variable, log() is the log function, and \(\varepsilon \) is the Error.
The logarithmic transformation enables the modeling of relationships in which the independent variables’ effects on the dependent variable are multiplicative rather than additive. It is frequently employed when the relationship between the variables is curvilinear, with declining returns or increasing rates of change45. Logarithmic regression can be applied to data analysis in various domains, including economics, finance, biology, and environmental sciences46. It enables researchers to record and evaluate non-linear correlations between variables, as well as make predictions or draw insights using the logarithmic scale.
Discussion on computed results
Using the SPSS software, basically two regression models (logarithmic and power) are applied to examine the relationship between \(\text{TI}\) and graph entropy. It is noticed that the curve of logarithmic model is more closer then the power model because curve of logarithmic model touches almost each point of the observed data set, so we conclude that logarithmic model is more significant then the power, that is why logarithmic regression is applied to check the relationship between graph topological indices and entropy. The basic purpose of applying regression is to check the best predictor, the variable having good relation are the best predictor. In this case variables are curvilinear, so the best model to show their relationship is logarithmic regression.. As curve of logarithmic model passes through exactly each point of \( {\text{GA}}({\text{BeN}}_{4} ) \), so we may say that the relationship between \( {\text{GA}}({\text{BeN}}_{4} ) \) and its corresponding entropy \( {\text{ENT}}_{{{\text{GA}}}} ({\text{G}}) \) is much more better than the other \(\text{TI}\). Here we use different symbols for indices and entropy in the Figures that are \(R1= {\text{R}}_{1} ({\text{BeN}}_{4} ) \), \(RN1= {\text{R}}_{-1} ({\text{BeN}}_{4} ) \), \(R12= {\text{R}}_{{\frac{1}{2}}} ({\text{BeN}}_{4} ) \), \(RN12= {\text{R}}_{{-\frac{1}{2}}} ({\text{BeN}}_{4} ) \), \(ABC= {\text{ABC}}({\text{BeN}}_{4} ) \), \( GA = {\text{GA}}({\text{BeN}}_{4} ) \), \(M1= {\text{M}}_{1} ({\text{BeN}}_{4} ) \), \(M2= {\text{M}}_{2} ({\text{BeN}}_{4} ) \), \(HM= {\text{HM}}({\text{BeN}}_{4} ) \), \(F= {\text{F}}({\text{BeN}}_{4} ) \), \(REZ1= {\text{ReZG}}_{1} ({\text{BeN}}_{4} ) \), \(REZ2= {\text{ReZG}}_{2} ({\text{BeN}}_{4} ) \) and, \(REZ3= {\text{ReZG}}_{3} ({\text{BeN}}_{4} ) \). Similarly, \(ENTR1= {\text{ENT}}_{{ {\text{R}}_{1} ({\text{BeN}}_{4} )}} \), \(ENTRN1= {\text{ENT}}_{{{\text{R}}_{{ - 1}} ({\text{BeN}}_{4} )}} \), \(ENTR12= {\text{ENT}}_{{{\text{R}}_{{\frac{1}{2}}} ({\text{BeN}}_{4} )}} \), \(ENTRN12= {\text{ENT}}_{{{\text{R}}_{{ - \frac{1}{2}}} ({\text{BeN}}_{4} )}} \), \(ENTABC= {\text{ENT}}_{{{\text{ABC}}({\text{BeN}}_{4} )}} \), \(ENTGA= {\text{ENT}}_{{{\text{GA}}({\text{BeN}}_{4} )}} \), \(ENTM1= {\text{ENT}}_{{{\text{M}}_{1} ({\text{BeN}}_{4} )}} \), \(ENTM2={\text{ENT}}_{{{\text{M}}_{2} ({\text{BeN}}_{4} )}}\), \(ENTHM= {\text{ENT}}_{{{\text{HM}}({\text{BeN}}_{4} )}} \), \(ENTF= {\text{ENT}}_{{{\text{F}}({\text{BeN}}_{4} )}} \), \(ENTREZ1= {\text{ENT}}_{{{\text{ReZG}}_{1} ({\text{BeN}}_{4} )}} \), \(ENTREZ2={\text{ENT}}_{{{\text{ReZG}}_{2} ({\text{BeN}}_{4} )}}\) and, \(ENTREZ3={\text{ENT}}_{{{\text{ReZG}}_{3} ({\text{BeN}}_{4} )}}\).
It can be seen that \( {\text{GA}}({\text{BeN}}_{4} ) \) and \( {\text{ENT}}_{{{\text{GA}}({\text{BeN}}_{4} )}} \) has best relationship having \(R=1\), \(R^2=1\), \(S_{E}=0.011\) and \(F=186557:243\). A model with maximum value of R, \(R^2\) and F, while minimum \(S_{E}\) is best model. So we may conclude that \( {\text{GA}}({\text{BeN}}_{4} ) \) is the best predictor of complexity of \(BeO_4\).
The statistical values for each model are depicted in Tables 12, 13, 14, 15, 16, 17, 18, and 19 while the graphical depiction in the Figs. 10, 11, 12, 13, 14, 15, and 16.
Conclusion
This study delved into the intricate realm of Beryllonitrene’s molecular structure through the lens of graph theory and mathematical modeling. The computation and analysis of topological indices and graph entropy have illuminated crucial insights into the compound’s unique structural and energetic attributes. By employing logarithmic regression models, we established meaningful correlations between these indices, entropy, and other molecular characteristics, offering a comprehensive perspective on Beryllonitrene’s complex properties.
The findings underscore the significance of computational methodologies in deciphering the properties of novel materials, such as Beryllonitrene, which holds promise for diverse applications. The successful application of logarithmic regression models showcases their utility in capturing nuanced relationships within complex systems. Furthermore, the insights gained from this study provide a valuable foundation for potential applications of Beryllonitrene in various scientific and technological domains.As we move forward, this research sets the stage for further investigations into the molecular properties of Beryllonitrene and similar compounds. Additionally, the methodologies employed here could be extended to the analysis of other novel materials, contributing to the advancement of materials science and fostering innovation across disciplines. Ultimately, the integration of computational techniques and mathematical models in this study serves as a testament to their pivotal role in unraveling the mysteries of emerging materials and compounds.
The degree-based topological indices \(\text{TI}\) are determined, as well as the entropy of graph based on these \(\text{TI}\) to the complexity of \(BeN_4\). It is noticed that by increasing the number of unit cell of \(BeN_4\) the value of \(\text{TI}\) and its corresponding entropy is also increasing which shows that as number of unit cell increases complexity of the \(BeN_4\) also increases. Using the SPSS software, logarithmic and power regression is applied to examine the relationship between \(\text{TI}\) and graph entropy. It is noticed that the line of logarithmic model is more closer then the power model because curve of logarithmic model touches almost each point of the observed data set so we conclude that logarithmic model is more significant then the power. As curve of logarithmic model passes through exactly each point of \( {\text{GA}}({\text{BeN}}_{4} ) \), so we may say that the relationship between \( {\text{GA}}({\text{BeN}}_{4} ) \) and its corresponding entropy \( {\text{ENT}}_{{{\text{GA}}}} ({\text{G}}) \) is much more better than the other \(\text{TI}\) e.g (\( {\text{R}}_{1} ({\text{BeN}}_{4} ) \), \( {\text{R}}_{-1} ({\text{BeN}}_{4} ) \), \( {\text{R}}_{{\frac{1}{2}}} ({\text{BeN}}_{4} \), \( {\text{R}}_{{ - \frac{1}{2}}} ({\text{BeN}}_{4} ) \), \( {\text{ABC}}({\text{BeN}}_{4} ) \), \( {\text{AZI}}({\text{BeN}}_{4} ) \), \( {\text{M}}_{1} ({\text{BeN}}_{4} ) \), \( {\text{M}}_{2} ({\text{BeN}}_{4} ) \), \( {\text{HM}}({\text{BeN}}_{4} ) \), \( {\text{F}}({\text{BeN}}_{4} ) \), \( {\text{ReZG}}_{1} ({\text{BeN}}_{4} ) \), \( {\text{ReZG}}_{2} ({\text{BeN}}_{4} ) \), and \( {\text{ReZG}}_{3} ({\text{BeN}}_{4} ) \)) because it has highest value of \(R=1\), \(R^2=1\) and \(F=186557:243\), while the vale of \(S_{E}=0.011\) is minimum as compared to the other \(\text{TI}\). So we may conclude that \( {\text{GA}}({\text{BeN}}_{4} ) \) is best predictor of complexity \(BeN_4\) of among all these indices.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Cai, Z. Q., Rauf, A., Ishtiaq, M. & Siddiqui, M. K. On ve-degree and ev-degree based topological properties of silicon carbide Si2C3-II [p, q]. Polycyclic Aromatic Compounds 42(2), 593–607 (2022).
Zhang, X. et al. On face index of silicon carbides. Discrete Dynamics Nat. Soc. 2020, 8 (2020).
Idrees, N., Naeem, M. N., Hussain, F., Sadiq, A. & Siddiqui, M. K. Molecular descriptors of benzenoid systems. Quimica Nova 40, 143–145 (2017).
Prathik, A., Uma, K. & Anuradha, J. An Overview of application of Graph theory. Int. J. ChemTech Res. 9(2), 242–248 (2016).
Mondal, S., Siddiqui, M. K., De, N. & Pal, A. Neighborhood M-polynomial of crystallographic structures. Biointerface Res. Appl. Chem. 11(2), 9372–9381 (2021).
Gutman, I. Degree-based topological indices. Croatica Chemica Acta 86(4), 351–361 (2013).
Gnanaraj, L. R. M., Ganesan, D., & Siddiqui, M. K. (2023). Topological indices and QSPR analysis of NSAID drugs. Polycyclic Aromatic Compounds. 1–17.
Zhang, X., Awais, H. M., Javaid, M. & Siddiqui, M. K. Multiplicative Zagreb indices of molecular graphs. J. Chem. 2019, 1–19 (2019).
Zhang, X., Jiang, H., Liu, J. B. & Shao, Z. The cartesian product and join graphs on edge-version atom-bond connectivity and geometric arithmetic indices. Molecules 23(7), 17–31 (2018).
Zhang, X. et al. Physical analysis of heat for formation and entropy of Ceria Oxide using topological indices. Combinatorial Chem. High Throughput Screening 25(3), 441–450 (2022).
Zhang, X., Naeem, M., Baig, A. Q. & Zahid, M. A. Study of hardness of superhard crystals by topological indices. J. Chem. 2021, 1–10 (2021).
Nagarajan, S., Priyadharsini, G., & Pattabiraman, K. (2022). QSPR modeling of status-based topological indices with COVID-19 drugs. Polycyclic Aromatic Compounds. 1–20.
Furtula, B. & Gutman, I. A forgotten topological index. J. Math. Chem. 53(4), 1184–1190 (2015).
Liu, J. B., Bao, Y. & Zheng, W. T. Analyses of some structural properties on a class of hierarchical scale-free networks. Fractals 30(7), 225–23 (2022).
Liu, J. B., Bao, Y., Zheng, W. T. & Hayat, S. Network coherence analysis on a family of nested weighted n-polygon networks. Fractals 29(08), 215–225 (2021).
Zhang, X. et al. On degree and distance-based topological indices of certain interconnection networks. Eur. Phys. J. Plus 137(7), 1–15 (2022).
Imran, M., Malik, M. A., Aslam, G. I. H., Ali, A., & Aqib, M. (2023). On Zagreb coindices and Mostar index of \(TiO_{2}\) nanotubes. 13, 13–32.
Ali Malik, M., Aqib, M., Batool, I. & Muhammad Humza, H. Distance-based topological descriptors of capra operation on some graphs. Polycyclic Aromatic Compounds 10, 1–15 (2023).
Nadeem, M. F. et al. Topological aspects of metal-organic structure with the help of underlying networks. Arab. J. Chem. 14(6), 103–123 (2021).
Ahmad, Z., Mufti, Z. S., Nadeem, M. F., Shaker, H. & Siddiqui, H. M. A. Theoretical study of energy, inertia and nullity of phenylene and anthracene. Open Chem. 19(1), 541–547 (2021).
Ahmad, Z. et al. Eccentric connectivity indices of titania nanotubes TiO2 [m; n]. Eurasian Chem. Commun. 2(6), 712–721 (2020).
Koam, A. N., Ahmad, A. & Nadeem, M. F. Comparative study of valency-based topological descriptor for hexagon star network. Comput. Syst. Sci. Eng. 36(2), 293–306 (2021).
Liu, J. B., Zhao, J., Min, J. & Cao, J. The Hosoya index of graphs formed by a fractal graph. Fractals. 27(08), 1–12 (2019).
Liu, J. B., Wang, C., Wang, S. & Wei, B. Zagreb indices and multiplicative zagreb indices of eulerian graphs. Bull. Malay. Math. Sci. Soc. 42, 67–78 (2019).
Raos, N. & Miličević, A. Estimation of stability constants of coordination compounds using models based on topological indices. Arhiv za higijenu rada i toksikologiju 60(1), 123–128 (2009).
Li, X., Gutman, I. & Randic, M. Mathematical aspects of Randic-type molecular structure descriptors (University, Faculty of Science, 2006).
Estrada, E., Torres, L., Rodriguez, L. & Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem 37A, 849–855 (1998).
Gao, W., Wang, W. F., Jamil, M. K., Farooq, R. & Farahani, M. R. Generalized atom-bond connectivity analysis of several chemical molecular graphs. Bulgarian Chem. Commun. 48(3), 543–549 (2016).
Vukicevic, D. & Furtula, B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 46(4), 1369–1376 (2009).
Das, K. C. & Gutman, I. Some properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem. 52(1), 3 (2004).
Gutman, I. & Trinajstic, N. Graph theory and molecular orbitals. Total electron energy of alternant hydrocarbons. Chem. Phys. Lett. 17(4), 535–538 (1972).
Gutman, I. et al. Graph theory and molecular orbitals. XII. Acyclic polyenes. J. Chem. Phys. 62(9), 3399–3405 (1975).
Shirdel, G. H., Rezapour, H. & Sayadi, A. M. The hyper Zagreb index of graph operations. Iranian J. Math. Chem. 4(2), 213–220 (2013).
Ranjini, P. S., Lokesha, V. & Usha, A. Relation between phenylene and hexagonal squeeze using harmonic index. Int. J. Graph Theory 1(4), 116–121 (2013).
Tong, Z. et al. Significant increase of electron thermal conductivity in Dirac semimetal beryllonitrene by doping beyond van hove singularity. Adv. Functional Mater. 32(17), 211–222 (2022).
Pu, A. & Luo, X. Li-doped beryllonitrene for enhanced carbon dioxide capture. RSC Adv. 11(60), 37842–37850 (2021).
Shannon, C. E. A mathematical theory of communication. Bell Syst. Tech. J. 27(3), 379–423 (1948).
Dehmer, M. & Grabner, M. The discrimination power of molecular identification numbers revisited. MATCH Commun. Math. Comput. Chem. 69(3), 785–794 (2013).
Myers, R. H., & Myers, R. H. Classical and modern regression with applications (Vol. 2, p. 488). (Duxbury Press, 1990).
Paliwal, M. & Kumar, U. A. Neural networks and statistical techniques: A review of applications. Expert Syst. Appl. 36(1), 2–17 (2009).
Gogtay, N. J., Deshpande, S. & Thatte, U. M. Principles of regression analysis. J. Assoc. Phys. India. 65(48), 48–52 (2017).
Yan, X., & Su, X. (2009). Linear regression analysis: theory and computing. World Scientific.
Twomey, P. J. & Kroll, M. H. How to use linear regression and correlation in quantitative method comparison studies. Int. J. Clin. Practice 62(4), 529–538 (2008).
Mehmanpazir, F., Khalili-Damghani, K. & Hafezalkotob, A. Modeling steel supply and demand functions using logarithmic multiple regression analysis (case study: Steel industry in Iran). Resources Policy 63, 101409 (2019).
Alexopoulos, E. C. Introduction to multivariate regression analysis. Hippokratia 14(Suppl 1), 23 (2010).
Kong, D., Zhao, J., Tang, S., Shen, W. & Lee, H. K. Logarithmic data processing can be used justifiably in the plotting of a calibration curve. Analyt. Chem. 93(36), 12156–12161 (2021).
Acknowledgements
This research project is supported by the Natural Science Research Project of Anhui Educational Committee (No. KJ2017B004), Major Project of online in Teaching Reform (No. 2020zdxsjg041), Humanities and Social Science Project of Anhui Provincial Education Department (No. SK2021A1094).
Author information
Authors and Affiliations
Contributions
Guofeng Yu contributed to Investigation, analyzing the data curation, and designing the experiments. Muhammad Kamran Siddiqui contributed to supervision, conceptualization, Methodology, project administration, and resources, and wrote the initial draft of the paper. Mazhar Hussain contributed for computation, and investigated and approved the final draft of the paper. Nazir Hussain contributes to Matlab calculations, Maple graphs improvement. Zohaib Saddique contributed to data analysis, computation, funding resources, calculation verifications. Fikre Bogale Petros contributes to formal analyzing experiments, software, validation and funding. All authors read and approved the final version.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yu, G., Siddiqui, M.K., Hussain, M. et al. On topological indices and entropy measures of beryllonitrene network via logarithmic regression model. Sci Rep 14, 7187 (2024). https://doi.org/10.1038/s41598-024-57601-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-57601-1
Keywords
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.