Introduction

The IP has received a lot of attention in recent years because of two essential components: high ordering and significant relationship, both of which are significant concerns in the control area. Moreover, the mechanism is unstable, nonlinear, and multivariable. Many processes in the military, aircraft, robotics, and general industries can benefit from using IP control techniques, including those that deal with robot walking balance challenges, rocket launch important considerations, and satellite flying control problems. Thus, it is extremely important to use this approach to investigate the IP scheme1,2,3. Furthermore, the mechanism for producing force based on the electromagnetic impact to preserve the IP in balancing is produced in the IP system by applying the force to the upper end of the IP and the electromagnetic influence on the IP. The IP is used in numerous engineering applications, including single-wheeled mobile robots, personal transporters, and walking robots4. Balanced management of an IP is a daunting challenge because the dynamics of IP are fundamentally open-loop unstable, nonlinear, underactuated, and non-minimum phase. It is frequently used as a reference point for developing and approving various control systems. The IP has been widely utilized in controlling education for many years due to its significance in control engineering.

Analytical calculations and actual observations were used to examine the nonlinear vibrational behavior of a linearly regulated rotary IP5. The fundamental coupled nonlinear equations of the structure, which were developed employing Lagrange's variational principle, were solved by developing the MSPT. Among the traditional systems where parameterized instability develops is the vertically propelled pendulum. Whenever the bob is a magnetic dipole, an extra electromagnetic relationship created by eddy currents in a neighboring thick conducting plate was investigated6. Studies addressing the scientific framework, recommending a hybrid control technique, and creating a workable model of an IP were examined7. Results from simulations and actual experiments were achieved, confirming the IP model performance and adaptability when combined with a suitable hybrid control method in a balanced situation. The IP was a straightforward and useful laboratory simulation of a mechanical system that was unstable. The explanation of the historical development of IP and the contrast between a number of its earlier procedures, which were carried out between 1960 and 1970 according to the earlier bibliography, were examined8. In order to comprehend how design decisions, affect balancing effectiveness, five areas of development for wheeling IP systems were examined9. Elasticity needs to be incorporated into mathematical models for the system of dynamics analysis. Elasticity was taken into consideration when a new type of IP, the elastic IP, was developed10. For a reaction wheel IP subject to biased angle measurements, a linear analysis was developed11. In this study, the stability issue was considered when there was an ongoing, unidentified bias in measurements of the pendulum angle. It has significant practical implications because it permits both a closer approximation of the control of robots and a less exact arrangement of sensors. A generalized mathematical model of IP was used to study how the pendulum factors and follower force affect the development of equilibrium situations. The parameter extension approach was used to plot equilibrium curves12.

Numerous engineering and physical phenomena are described via nonlinear differential equations. Most of those concerns, with the exception of a few numbers, lack obtaining an exact analytical solution. Really, this requires approximate methods to determine such equations because the HPM13 has better quality calculation than the earlier techniques. Additionally, it is a straightforward, strong, efficient, attractive, powerful, and promising approach. Therefore, scientists and engineers have given much attention to this methodology in application in nonlinear problems. The Laplace transforms dispersive heat radiation, integral heat conduction, nonlinear oscillators, nonlinear Schrodinger equations, nonlinear chemistry, and many other nonlinear issues have already been addressed by using the HPM14. In most situations, it results in a very quick convergence of the series solution, typically with just a few iterations leading to highly precise solutions. Consequently, HPM is efficient in resolving many types of nonlinear equations. A minor equational parameter has no bearing on the technique. The homotopy was built using the homotopy procedure in topology with an embedded parameter \(\rho \in \left[ {0,\,1} \right]\) that was regarded as a "small parameter". It has been used to approximately solve a wide range of nonlinear problems efficiently, quickly, and appropriately. These approximations quickly reach the correct answers as found earlier in15,16. A hybrid Rayleigh–Van der Pol–Duffing oscillator with an exciting exterior force and nonlinear terms was studied17. To reach an approximate solution, the method of Poincaré–Lindstedt was adopted during their approach.

In order to demonstrate that the vibration induced by the external force was suppressed, a time history comparison was made for both the uncontrolled and the controlled models. Three different types of controllers were added to study the best of them in damping the vibration occurring in the harmonic force Duffing oscillator system18. They used the MSPT to find the approximate solution for this system after connecting it to the nonlinear integrated positive position feedback (NIPPF) controller. The PPF controller dampens the vibration that occurred in a nonlinear exciting beam. To clarify the best conditions to reduce this vibration, they examined the effect of different parameters in the resonance case19. The influence of the PPF technique was utilized to analyze a solar panel prototype20. On the other hand, EL-Ganaini et al.21 used a PPF control to decrease the nonlinear vibration of a dynamical framework within a 1:1 internal resonance. The approximate solution was achieved by applying the MSPT. Moreover, EL-Sayed22 investigated a pair of delay PPF control that can minimize the vibration of double Van der Pol oscillators with external forces. The impacts of both the delayed feedback signal and the control gains were studied to demonstrate the low vibration amplitudes.

In light of the above-mentioned aspects, the current paper focuses on examining the problem of the motion of an IP. Furthermore, the main aim of this study is to suppress the harmful vibration in the IP system by using a PPF controller which has also been used in the previous references. The rest of the manuscript is structured as follows: The methodology of the problem is described in section "Methodology of the problem". In view of the HPM and the idea of the extended nonlinear frequency, an approximate uniform solution to the problem is described in section "Expanded frequency analysis". Section "Linearized stability of the autonomous equation" is dedicated to illustrating the linearized problem. The IP system with the controller is applied in section "IP system with PPF controller". The frequency response equations (FREs) and stability studies are shown in section "Linearized stability of the non-autonomous equation". Section "Results and discussions" introduces the results and discussions for the controller design. Finally, section "Conclusions" summarizes the key results.

Methodology of the problem

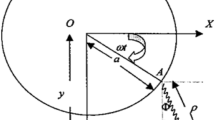
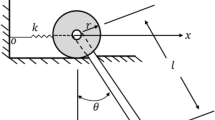
A magnetic IP is regarded as a mechanical system, where its bob has a point mass \(m\) and an electrical charge \(e\). It is connected to the length \(L\) of the weightless stiff rod. The other end of the rod swings vertically with a periodic displacement \(Q_{0} \cos \Omega t\) where \(Q_{0}\) and \(\Omega\) are the movement amplitude and frequency, respectively. The IP revolves around a fixed point \(0\). It rotates under the influence of a constant gravity force \(\underline{g}\) and a steady negative oriented magnetic field \(\underline{B}\) that acts in the negative z-direction. Because of the strong instability of the configuration of the IP, a light torsional spring of constant stiffness \(k\) is attached between its base and the y-axis. The sketch of the theoretical prototype of the IP may be exemplified in Fig. 1.

Figure 1
figure 1

Sketches the IP with a vertical periodic moving base.

Full size image
Figure 2
figure 2

Perturbed/numerical solutions of Eq. (14).

Full size image

As shown in this figure, the position vector of the bob of the IP is given as:

$$\underline{r} = L\,\sin \theta \,\underline{i} + (L\cos \theta + Q_{0} \cos \Omega t\,)\underline{j} ,$$
(1)

where \(\theta\) is measured between the IP and the y-axis.

It follows that velocity may be given by:

$$\underline{v} = L\dot{\theta }\,\cos \theta \,\underline{i} - (L\dot{\theta }\sin \theta \, + \Omega \,Q_{0} \sin \Omega t)\underline{j} ,$$
(2)

Subsequently, the kinetic energy becomes:

$$T = \frac{m}{2}\left[ {L^{2} \dot{\theta }^{2} + 2L\Omega Q_{0} \dot{\theta }\sin \theta \sin \Omega t + \Omega^{2} Q_{0}^{2} \sin^{2} \Omega t} \right].$$
(3)

The potential energy probably originated from a number of actions, which can be grouped into the following categories:

  • The energy in the relation to a gravitational field, or gravitational potential energy has a definition of \(mgL\cos \theta\).

  • The potential energy stored as a result of flexible body deformation, such as a spring expanding, is known as elastic energy. The effort put forth in stretching the spring could serve as its metaphor. It is based on the constricted length and the constant stiffness of the spring \(k\). It can be written as \(k\theta^{2} /2\).

  • The potential function of the issue, therefore, must include the magnetic term \(q\,\underline{P} \,.\,\underline{v}\), where \(\underline{P}\) is the magnetic vector potential; for example, see Eyal and Goldstein23, due to the charged IP traveling in a homogeneous magnetic field \(\underline{B} = B\,\underline{k}\). Remember that it determines the connection between the magnetic field \(\underline{B}\) and the magnetic potential \(\underline{P}\) and is given by \(\underline{B} = \nabla \wedge \underline{P}\). The practical significance of a homogenous magnetic field is widely established. One may demonstrate that one of the vector potential alternatives is provided by \(\underline{P} = \tfrac{1}{2}\left( {\underline{B} \wedge \underline{r} } \right)\). The sentence that follows can be expressed as follows24:

    $$\underline{P} = \tfrac{1}{2}B\left( {( - L\cos \theta - Q_{0} \cos \Omega t)\,\underline{i} + L\sin \theta \,\underline{j} } \right).$$
    (4)

The potential energy caused by the uniform magnetic field can be expressed by merging Eqs. (2) and (4) as follows:

$$\underline{P} .\,\underline{E}_{mag} = - \tfrac{1}{2}q\,L\,B\left[ {\left. {L\dot{\theta } + Q_{0} \,\dot{\theta }\,\cos \theta \cos \Omega t + \Omega \,Q_{0} \sin \theta \sin \Omega t} \right]} \right.,$$
(5)

Accordingly, the formulation for the total expected energy is as follows:

$$V = m\,g\,L\cos \theta + \tfrac{1}{2}k\,\theta^{2} - \tfrac{1}{2}q\,L\,B\left[ {L\dot{\theta } + Q_{0} \,\dot{\theta }\cos \theta \cos \Omega t + \Omega \,Q_{0} \sin \theta \sin \Omega t} \right].$$
(6)

Incorporating Eqs. (3) and (6), it is evident that the magnetic IP under consideration has the following Lagrangian function:

$$\begin{aligned} \Re & = T - V \\ & = \tfrac{1}{2}m\,\left[ {L^{2} \dot{\theta }^{2} + 2L\Omega Q_{0} \dot{\theta }\sin \theta \sin \Omega t + \Omega^{2} Q_{0}^{2} \sin^{2} \Omega t} \right] \\ & \,\,\,\,\,\, - \left\{ {m\,g\,L\cos \theta + \tfrac{1}{2}k\,\theta^{2} - \tfrac{1}{2}q\,LB\left( {L\dot{\theta } + Q_{0} \,\dot{\theta }\cos \theta \cos \Omega t + \Omega \,Q_{0} \sin \theta \sin \Omega t} \right)} \right\}. \\ \end{aligned}$$
(7)

However, the force under consideration becomes a non-conservative force when the air-dampening force is considered. This force can be expressed in the following way:

$$\underline{G}_{D} = - \delta \,\underline{v} .$$
(8)

Therefore, one gets

$$\underline{G}_{D} = \delta \left( {( - L\dot{\theta }\,\cos \theta )\,\underline{i} + (L\dot{\theta }\sin \theta + \Omega \,Q_{0} \sin \Omega t\,\underline{)j} } \right).$$
(9)

The structure has only one degree of freedom, and the generalized coordinate is expressed by an angle of measure \(\theta\). In addition to this explanation, the generalized force is described as:

$$Q = \underline{G}_{D} \,.\,\frac{{\partial \underline{r} }}{\partial \theta } = - \delta \,L^{2} \dot{\theta } - \delta \,\Omega \,LQ_{0} \sin \theta \sin \Omega t.$$
(10)

From the analytical mechanics perspective, Lagrange’s equation with the non-conservative system may be written as25:

$$\frac{d}{dt}\left( {\frac{\partial \Re }{{\partial \dot{\theta }}}} \right) - \frac{\partial \Re }{{\partial \theta }} = Q.$$
(11)

When Eqs. (7) and (10) are inserted into Eq. (11), the controlling dynamic model of the magnetic IP under consideration can be described as follows:

$$m\,L^{2} \ddot{\theta } + \delta \,L^{2} \dot{\theta } + k\theta + L\,(m\,\Omega^{2} Q_{0} \cos \Omega t - mg + \delta \,\Omega \,Q_{0} \sin \Omega t)\,\sin \theta - L\,q\,B\,Q_{0} \,\Omega \,\sin \Omega t\,\cos \theta = 0.$$
(12)

A second-order differential equation with a harmonic restoring force and multiple parameterized forces is represented by Eq. (12).

Now let us go back to the initial controlling equation found in Eq. (12). The stability requirements of the magnetic IP under consideration will be analyzed using a unique technique in the following sections. A non-dimensional approach will be required before dealing with the quantitative equations of the governing equation of the IP as stated in Eq. (12), for more convenience. For this purpose, the non-dimensional technique is performed in a wide range of ways which largely depend on the characteristics of length, duration, and mass. In the problem under consideration, the characteristics are taken as follows \(Q_{0} ,\,\,\sqrt {Q_{0} /g}\) and \(m\). Therefore, Eq. (12) may be transformed into the reduced communication form in addition to these features:

$$\,L^{2} \ddot{\theta } + \delta \,L^{2} \dot{\theta } + k\theta + L\,(\,\Omega^{2} \cos \Omega t - 1 + \delta \,\Omega \sin \Omega t)\,\sin \theta - L\,H\,\Omega \,\,\sin \Omega t\,\cos \theta = 0.$$
(13)

where the non-dimensional term of the magnetic contributions \(H\), which results from the multiplication \(qB\), is referred to as the parameterization of the magnetic field.

Expanded frequency analysis

The primary aim of this Section is to achieve a circumscribed analytical approximate solution for the second-order differential as given in Eq. (13). For this purpose, we will use an approximation of the circle functions as: \(\sin \,\theta \approx \theta - \frac{1}{6}\theta^{3} + ...\) and \(\cos \,\theta \approx 1 - \frac{1}{2}\theta^{2} + ...\). Therefore, Eq. (13) then becomes:

$$\ddot{\theta } + \delta \,\dot{\theta } + \omega^{2} \theta - \frac{\Omega \,H}{L}\,\sin \Omega t\,\,\left( {1 - \frac{{\theta^{2} }}{2}} \right) - \left( { - 1 + \Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta^{3} }}{6\,L} + \left( {\Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{\theta }{\,L} = 0,$$
(14)

where the natural frequency of the current prototype becomes \(\omega^{2} = \frac{1}{{L^{2} }}\left( {k - L} \right)\).

The following performance is primarily dependent on a few HPM and Laplace transforms (\(L_{T}\)). Equation (14) may be then interpreted as:

$$I(\theta ) = \ddot{\theta } + \omega^{2} \,\theta ,$$
(15)

and

$$N(\theta ) = \delta \,\dot{\theta } - \frac{\Omega \,H}{L}\,\sin \Omega t\,\,\left( {1 - \frac{{\theta^{2} }}{2}} \right) - \left( { - 1 + \Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta^{3} }}{6\,L} + \left( {\Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{\theta }{\,L}.$$
(16)

For this objective, it is appropriate to presume the initial condition listed below:

$$\theta (0) = 0,\quad {\text{and}}\quad \dot{\theta }(0) = 1.$$
(17)

Therefore, the Homotopy equation may be formulated as follows:

$$I(\theta ) + \rho \,N(\theta ) = 0;\,\,\rho \in \left[ {0,\,1} \right],$$
(18)

where \(\rho\) is a synthetic embedded factor. Occasionally, it is known as the Homotopy constraint.

The HPM can offer a variety of approximate solutions, as was clearly demonstrated in our earlier work26,27. One of these approaches results in a conventional solution with secular terms; the elimination of these secular terms produces a trivial solution, which is not appropriate. By using the expanded frequency conception, an alternative solution generates a solution that is consistently satisfactory; however, it does not satisfy the numerical solution. Therefore, the HPM must consequently be changed once more. In order to investigate the impacts of the delay parameter, which is better at avoiding bifurcations and reducing vibration, we may therefore re-analyze the basic Homotopy equation using a novel expansion in replacement of the conventional expansion. In light of our previous work23, we believe that \(\theta \left( {t,\rho } \right)\) needs to be further developed. The following are the procedures to obtain the required solution:

Throughout this process28, the time-dependent parameter may be formulated as:\(\theta (t) = \theta (t;\rho )\) and

$$\theta (t;\rho ) = e^{ - \delta \rho t/2} \left( {\theta_{0} (t) + \rho \,\theta_{1} (t) + \cdots } \right).$$
(19)

As earlier stated, the homotopy formula for the equation under consideration is provided by Eq. (18). The expanded frequency analysis will serve as the foundation for the instability analysis. This method necessitates the following equation, see Moatimid26,27:

$$\sigma^{2} = \omega^{2} + \sum\limits_{j = 1}^{\infty } {\rho^{j} \sigma_{j} } .$$
(20)

where the factors \(\sigma_{i}\) will be calculated later on after being combined with the initial features of the problem. By doing so, secular terms will be made meaningless.

When Eqs. (18–20) are combined, the Laplace transform is applied, the initial conditions from Eq. (17) are considered, and the outcome then becomes:

$$L_{T} \left\{ {\theta (t;\,\rho )} \right\} = \frac{1}{{s^{2} + \sigma^{2} }}\, - \frac{\rho }{{s^{2} + \sigma^{2} }}L_{T} \left\{ \begin{gathered} - \sigma_{1} \theta_{0} - \delta \,\dot{\theta }_{0} - \frac{\delta }{2}t\,\ddot{\theta }_{0} - \frac{\delta }{2}t\sigma^{2} \,\theta_{0} + \delta \,\dot{\theta }_{0} - \frac{\Omega \,H}{L}\,\sin \Omega t\,\,\left( {1 - \frac{{\theta_{0}^{2} }}{2}} \right) \hfill \\ - \left( { - 1 + \Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta_{0}^{3} }}{6\,L} + \left( {\Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta_{0} }}{\,L} \hfill \\ \end{gathered} \right\}.$$
(21)

Findings are obtained by employing the inverse transform to both sides of Eq. (21).

$$\theta (t;\,\rho ) = \frac{1}{\sigma }\sin (\sigma \,t) - L_{T}^{ - 1} \left\{ {\frac{\rho }{{s^{2} + \sigma^{2} }}L_{T} \left\{ \begin{gathered} - \sigma_{1} \theta_{0} - \delta \,\dot{\theta }_{0} - \frac{\delta }{2}t\,\ddot{\theta }_{0} - \frac{\delta }{2}t\sigma^{2} \,\theta_{0} + \delta \,\dot{\theta }_{0} - \frac{\Omega \,H}{L}\,\sin \Omega t\,\,\left( {1 - \frac{{\theta_{0}^{2} }}{2}} \right) \hfill \\ - \left( { - 1 + \Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta_{0}^{3} }}{6\,L} + \left( {\Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta_{0} }}{\,L}. \hfill \\ \end{gathered} \right\}} \right\}.$$
(22)

By producing the development of the dependent variable \(\theta (t;\rho )\) as presented in Eq. (22), and then recognizing the coefficients of comparable powers \(\rho\) on each side, one obtains

$$\rho^{0} :\,\,\theta_{0} (t) = \frac{1}{\sigma }\sin \sigma \,t,$$
(23)

and

$$\rho :\,\,\,\,\theta_{1} (t) = - L_{T}^{ - 1} \left\{ {\frac{1}{{s^{2} + \sigma^{2} }}L_{T} \left\{ \begin{gathered} - \sigma_{1} \theta_{0} - \delta \,\dot{\theta }_{0} - \frac{\delta }{2}t\,\ddot{\theta }_{0} - \frac{\delta }{2}t\sigma^{2} \,\theta_{0} + \delta \,\dot{\theta }_{0} - \frac{\Omega \,H}{L}\,\sin \Omega t\,\,\left( {1 - \frac{{\theta_{0}^{2} }}{2}} \right) \hfill \\ - \left( { - 1 + \Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta_{0}^{3} }}{6\,L} + \left( {\Omega^{2} \cos \Omega t + \delta \,\Omega \,\sin \Omega t} \right)\,\frac{{\theta_{0} }}{\,L}. \hfill \\ \end{gathered} \right\}} \right\}.$$
(24)

Characteristically, the consistent logical statement goes out from the removal of the secular terms. For this purpose, the coefficient of the function \(\sin \sigma \,t\) should be disregarded. This implementation goes to create the parameter \(\sigma_{1}\) as follows:

$$\sigma_{1} = \frac{1}{{8L\,\sigma^{2} }}.$$
(25)

The periodical response at this point in time is provided by

$$\begin{aligned} \theta_{1} (t) & = \theta_{11} \cos \,\sigma \,t + \theta_{12} \,\cos \,(\sigma - \Omega )\,t + \theta_{13} \,\cos \,(\sigma + \Omega )\,t + \theta_{14} \,\,\cos \,(3\,\sigma - \Omega )\,t + \theta_{15} \,\cos \,(3\,\sigma + \Omega )\,t \\ & \quad + \theta_{16} \,\sin \,\Omega \,t + \theta_{17} \sin \,\sigma \,t + \theta_{18} \,\sin \,3\,\sigma \,t + \theta_{19} \,\sin \,(\sigma - \Omega )\,t + \theta_{20} \,\sin \,(\sigma + \Omega )\,t + \theta_{21} \,\sin \,(2\,\sigma - \Omega )\,t \\ & \quad + \theta_{22} \,\sin \,(2\,\sigma + \Omega )\,t + \theta_{23} \,\sin \,(3\,\sigma - \Omega )\,t + \theta_{24} \,\sin \,(3\,\sigma + \Omega )\,t, \\ \end{aligned}$$
(26)

where \(\theta_{ij}\) are given in the Appendix to follow the paper easily.

Consequently, the circumscribed approximate solution of the equation of motion provided in Eq. (14) may be expressed as follows:

$$\theta (t) = \mathop {\lim }\limits_{\rho \to 1} e^{ - \delta \rho t/2} \left( {\theta_{0} (t) + \rho \,\theta_{1} (t) + \cdots } \right).$$
(27)

In reality, the constrained approximate solution as provided in Eq. (27) requires that the arguments of the trigonometric functions should be of real significance. For this objective, Eq. (25) is inserted into Eq. (20), and it follows that the characteristic nonlinear frequency fulfills a particular equation. To this approximation, the computation indicates that this equation exemplifies a polynomial of fourth degree in the nonlinear frequency. This equation may be written as:

$$\sigma^{4} - \omega^{2} \,\sigma^{2} - \frac{1}{8L} = 0.$$
(28)

It is convenient to match this procedure with the numerical approach that is identified as RK-4 to evaluate the practicality of the previously expanded frequency implications. The requirements for implementation are listed below. Consequently, in what follows, the analytic approximate solution as provided by Eq. (28) is drawn in blue. Additionally, the RK-4 of the considered structure as offered by Eq. (14) is highlighted in red. The following figure is a graph of a scheme receiving the following specifics:

$$k = 0.9,\,\,L = 0.5,\,\,,\,H = 0.2,\,\,\Omega = 0.01\,\,\,{\text{and}}\,\,\,\delta = 0.1.$$

The computations demonstrate that the synthetic frequency has the amount \(\sigma = 1.32038\) and other roots (two are complex conjugate and the third is negative. It is also helpful to compare the numerical solution of the original Eq. (14) generated by RK-4 with the corresponding linear ODE solution. Equation (27) provides the approximate analytical solution. In this comparison, the structure is displayed, as seen in Fig. 2. For an appropriate sample with the provided details, the two figures are obtained in light of the previous data. The findings are reasonably reliable with one another, as can be observed. Further, the mathematical software demonstrated that the absolute difference between the analytical and numerical results, up to a time of 100 units, is 0.186645.

Linearized stability of the autonomous equation

For more convenience, the linearized stability of the IP may be derived in the special case, in the absence of the periodicity of the pin motion (\(\Omega = 0\)). In this situation, the governing equation of motion then becomes

$$\ddot{\theta } + \delta \,\dot{\theta } + \omega^{2} \,\theta + \frac{1}{6\,L}\,\theta^{3} = 0.$$
(29)

Contemplating the conversion: \(\dot{\theta } = \phi\), it follows that Eq. (29) may be transformed to the following equation

$$\dot{\theta } = g(\theta ,\phi ),\quad \dot{\phi } = h(\theta ,\phi ),$$
(30)

where

$$g(\theta ,\phi ) = \phi ,\quad \dot{\phi } = h(\theta ,\phi ) = - \delta \,\phi - \omega^{2} \,\theta - \frac{1}{6\,L}\,\theta^{3} .$$
(31)

The fixed points (equilibrium points) occur at the points \((\theta_{0} ,\phi_{0} )\),where

$$g(\theta_{0} ,\phi_{0} ) = 0,\quad h(\theta_{0} ,\phi_{0} ) = 0.$$
(32)

It follows that

$$\phi_{0} = 0,$$
(33)

and

$$\delta \,\phi_{0} + \omega^{2} \,\theta_{0} + \frac{1}{6\,L}\,\theta_{0}^{3} = 0.$$
(34)

Consequently, the only fixed point is \((0,0)\). Here, the Jacobian matrix is defined as

$$J = \left( {\begin{array}{*{20}c} 0 & 1 \\ { - \omega^{2} - \frac{1}{2\,L}\,\theta_{0}^{2} } & { - \delta } \\ \end{array} } \right).$$
(35)

The eigenvalues \(\lambda_{r}\), (\(r = 1,\,2\)) are given by \(J - \lambda_{r} \,I_{2 \times 2} = 0\). Therefore, these eigenvalues are provided by

$$\lambda_{1,2} = \frac{1}{2}\left( { - \delta \pm \sqrt {\delta^{2} - 4\,\left( {\omega^{2} + \frac{1}{2\,L}\,\theta_{0}^{2} } \right)} \,} \right).$$
(36)

When the Jacobian eigenvalues have a negative real portion, the equilibrium point is typically transformed into a stable state. On the contrary, if at least one of the eigenvalues has a positive real portion, the equilibrium point is unstable. As demonstrated by He et al.17 and Ghaleb et al.29, it is more acceptable to consider a sample system to indicate the stability/instability arrangement in light of the equilibrium points. As a result, the condition is determined by the type of the eigenvalues. Table 1 below provides a summary of this process.

Table 1 Equilibria classification of the eigenvalues and their stability/instability.
Full size table
Figure 3
figure 3

Dynamical performance (stable center) with certain factors recorded in Table 1.

Full size image
Figure 4
figure 4

Dynamical performance (stable spiral) with certain factors recorded in Table 1.

Full size image
Figure 5
figure 5

Dynamical behavior (stable spiral) with given factors recorded in Table 1.

Full size image
Figure 6
figure 6

Dynamical performance (stable proper node) with certain parameters listed in Table 1.

Full size image
Figure 7
figure 7

Dynamical performance (unstable spiral) with certain factors recorded in Table 1.

Full size image
Figure 8
figure 8

Dynamical performance (unstable proper node) with specified factors recorded in Table 1.

Full size image

IP system with PPF controller

Returning again to the fundamental equation of motion as given in (14) and letting \(F_{1} = H\,\Omega \,/L\),\(F_{2} = \Omega^{2} /L\),\(\,F_{3} = \delta \,\Omega \,/L\),\(\,\beta = 1/6\,L\), one gets

$$\,\ddot{\theta } + \delta \,\dot{\theta } + \omega^{2} \,\theta + \beta \,\theta^{3} = F_{1} \,\,\sin \Omega \,t\,\left( {1 - \theta^{2} /2} \right) - \left( {\,F_{2} \cos \Omega \,t + F_{3} \sin \Omega \,t} \right)\,\left( {\theta - \theta^{3} /6} \right).$$
(37)

Adding the PPF controller as previously shown19,20,21 to the preceding equation of motion, the following equations are established as follows:

$$\,\ddot{\theta } + \varepsilon \,\tilde{\delta }\,\dot{\theta } + \omega^{2} \,\theta + \varepsilon^{ - 1} \tilde{\beta }\,\theta^{3} = \varepsilon^{2} \,\tilde{F}_{1} \,\,\sin \Omega t\,\left( {1 - \theta^{2} /2} \right) - \varepsilon \left( {\,\tilde{F}_{2} \cos \Omega t + \tilde{F}_{3} \sin \Omega t} \right)\,\left( {\theta - \theta^{3} /6} \right)\, + \varepsilon \,\tilde{q}_{1} \,v\,,$$
(38)

and

$$\,\ddot{v} + \varepsilon \,\tilde{\delta }_{1} \,\dot{v} + \omega_{1}^{2} \,v = \varepsilon \,\tilde{q}_{2} \,\theta \,.$$
(39)

where the coefficients scale are as follows: \(\delta = \varepsilon \,\tilde{\delta },\beta = \varepsilon^{ - 1} \tilde{\beta },F_{1} = \varepsilon^{2} \,\tilde{F}_{1} ,F_{2} = \varepsilon \,\tilde{F}_{2} ,F_{3} = \varepsilon \,\tilde{F}_{3} ,q_{1} = \varepsilon \,\tilde{q}_{1}\), \(\delta_{1} = \varepsilon \,\tilde{\delta }_{1} \,,{\text{and}}\,\,q_{2} = \varepsilon \,\tilde{q}_{2}\).

\(\theta\) and \(v\) are the amplitudes of the model of the IP and controller, respectively. \(\delta\) and \(\delta_{1}\) are the coefficients of damping, \(\omega\) and \(\omega_{1}\) are natural frequencies, \(\beta\) is the coefficients of the nonlinear parameter, \(\Omega\) is the excitation frequency, \(F_{1}\), \(F_{2}\) and \(F_{3}\) are the parametric excitations, \(q_{1}\) and \(q_{2}\) are the parameters of control signals sign.

Numerical simulation with time history

In what follows, the numerical RK-4 is employed to graph the time history curve as well as the phase portrait before and after combining the PPF control at the primary resonance (\(\Omega \cong \omega\)) and the internal resonance (\(\omega_{1} \cong \omega\)). These calculations are performed based on MATLAB® computer program control. For this purpose, the sample chosen system is taken as follows:

$$\delta = 0.02,\,\,\omega = 1.0,\beta = 0.3,F_{1} = 0.5,F_{2} = 0.1,F_{3} = 0.1,q_{1} = 0.2,\delta_{1} = 0.02,q_{2} = 0.5.$$

The time history is illustrated through Fig. 9a for the steady state amplitude of IP system before adding the control. As shown from this figure, the amplitude reaches 1.074. Simultaneously, Fig. 9b represents the phase portrait between the velocity and amplitude for the same case, which shows the chaotic attractor and approximately multi-limit cycle. In addition, the response of the IP with and without the PPF controller is depicted as a Poincare map diagram in Fig. 9c. This figure is depicted to mention the type of motion of the system and the controller. On the other hand, Fig. 10a depicts the amplitude of the considered structure after combining the PPF control. It is found that that amplitude becomes 0.103. Therefore, according to this controller, the amplitudes have been reduced by the ratio 90.5%. Additionally, Fig. 10b displays the phase portrait between the velocity and amplitude after adding the PPF controller, which shows improvement of the chaotic attractor and limited cycle numbers. Finally, the effectiveness of the PPF controller \(E_{a}\) is defined as (\(E_{a} =\) steady-state amplitude of the structure before PPF separated by after controlling) and is of 10.43. Similar results were obtained earlier in our previous work19. As previously shown, Fig. 9c introduced Poincaré map for detecting chaos behavior in IP system before adding PPF controller. Furthermore, Fig. 10c presented the Poincaré map to show that the IP system after applying the PPF controller is no longer chaotic, which indicates a better quality of this controller.

Figure 9
figure 9

Time history, phase portrait and Poincare map of style without controller at \(\Omega = \omega\).

Full size image
Figure 10
figure 10

Time history, phase portrait and Poincare map of controlled style at \(\Omega = \omega\) and \(\omega_{1} = \omega\) .

Full size image

Perturbation analysis with MSPT

The MSPT19,20,21,25,30,31,32 is applied to obtain an approximate solution of Eqs. (38) and (39) as follows:

$$\theta (t;\varepsilon ) = \varepsilon \,\theta_{0} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{2} \,\theta_{1} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{3} \,\theta_{2} (T_{0} ,T_{1} ,T_{2} ) + O(\varepsilon^{4} ),$$
(40)

and

$$v(t;\varepsilon ) = \varepsilon \,v_{0} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{2} \,v_{1} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{3} \,v_{2} (T_{0} ,T_{1} ,T_{2} ) + O(\varepsilon^{4} ).$$
(41)

The time derivatives may be transformed as follows:

$$\frac{d}{d\,t} \equiv D_{0} + \varepsilon \,D_{1} + \varepsilon^{2} D_{2} ,$$
(42)

and

$$\frac{{d^{2} }}{{d\,t^{2} }} \equiv D_{0}^{2} + 2\,\varepsilon \,D_{0} D_{1} + \varepsilon^{2} (D_{1}^{2} + 2D_{0} D_{2} ),$$
(43)

where \(T_{k} = \varepsilon^{k} \,t\) and \(D_{k} \equiv \frac{\partial }{{\partial T_{k} }}\), (\(k = 0,1,2\)).

Substituting from Eqs. (40)–(43) into Eqs. (38) and (39), and then equating the similar powers for \(\varepsilon\) in the two sides, one obtains the following equations:

Order (\(\varepsilon\)):

$$(D_{0}^{2} + \omega^{2} )\,\theta_{0} = 0,$$
(44)

and

$$(D_{0}^{2} + \omega_{1}^{2} )\,v_{0} = 0.$$
(45)

Order (\(\varepsilon^{2}\)):

$$\begin{aligned} (D_{0}^{2} + \omega^{2} )\,\theta_{1} & = i\,\tilde{F}_{1} (e^{{ - i\Omega T_{0} }} - e^{{i\Omega T_{0} }} )/2 - \tilde{F}_{2} \,\theta_{0} (e^{{ - i\Omega T_{0} }} + e^{{i\Omega T_{0} }} )/2 - i\,\tilde{F}_{3} \,\theta_{0} (e^{{ - i\Omega T_{0} }} - e^{{i\Omega T_{0} }} )/2 \\ & \,\,\,\,\,\, + \tilde{q}_{1} \,v_{0} - \tilde{\beta }\,\theta_{0}^{3} - \tilde{\delta }\,D_{0} \theta_{0} - 2\,D_{0} D_{1} \theta_{0} , \\ \end{aligned}$$
(46)

and

$$(D_{0}^{2} + \omega_{1}^{2} )\,v_{1} = \tilde{q}_{2} \,\theta_{0} - \tilde{\delta }_{1} \,D_{0} v_{0} - 2\,D_{0} D_{1} v_{0} .$$
(47)

Order (\(\varepsilon^{3}\)):

$$\begin{aligned} (D_{0}^{2} + \omega^{2} )\,\theta_{2} & = \tilde{q}_{1} \,v_{1} - \tilde{F}_{2} \,\theta_{1} (e^{{ - i\Omega T_{0} }} + e^{{i\Omega T_{0} }} )/2 - i\,\tilde{F}_{3} \,\theta_{1} (e^{{ - i\Omega T_{0} }} + e^{{i\Omega T_{0} }} )/2 - 3\,\tilde{\beta }\,\theta_{0}^{2} \theta_{1} - \tilde{\delta }\,D_{1} \theta_{0} \\ & \,\,\,\,\,\, - \,D_{1}^{2} \theta_{0} - \tilde{\delta }\,D_{0} \theta_{1} - 2\,D_{0} D_{2} \theta_{0} - 2\,D_{0} D_{1} \theta_{1} , \\ \end{aligned}$$
(48)

and

$$(D_{0}^{2} + \omega_{1}^{2} )\,v_{2} = \tilde{q}_{2} \,\theta_{1} - \tilde{\delta }_{1} \,D_{1} v_{0} - \,D_{1}^{2} v_{0} , - \tilde{\delta }_{1} \,D_{0} v_{1} - 2\,D_{0} D_{2} v_{0} - 2\,D_{0} D_{1} v_{1} .$$
(49)

The solutions of Eqs. (44) and (45) may be formulated in the following forms:

$$\theta_{0} = A(T_{1} ,T_{2} )\,e^{{i\omega \,T_{0} }} + \overline{A}(T_{1} ,T_{2} )\,e^{{ - i\omega \,T_{0} }} ,$$
(50)

and

$$v_{0} = B(T_{1} ,T_{2} )\,e^{{i\omega_{1} \,T_{0} }} + \overline{B}(T_{1} ,T_{2} )\,e^{{ - i\omega_{1} \,T_{0} }} .$$
(51)

where \(A(T_{1} ,T_{2} )\) and \(B(T_{1} ,T_{2} )\) are arbitrary complex functions of \(T_{1}\), and \(T_{2}\).

Substituting Eqs. (50) and (51) into Eqs. (46) and (47), one gets the next equations:

$$\begin{aligned} (D_{0}^{2} + \omega^{2} )\,\theta_{1} & = - \,\tilde{\beta }\,A^{3} \,e^{{3i\omega \,\,T_{0} }} + \tilde{q}_{1} \,B\,e^{{i\omega_{1} \,T_{0} }} - i\,\tilde{F}_{1} \,e^{{i\Omega T_{0} }} /2 - (\tilde{F}_{2} \, - i\,\tilde{F}_{3} )\,A\,e^{{i(\omega + \Omega )\,T_{0} }} /2 \\ & \,\,\,\, - (\tilde{F}_{2} \, - i\,\tilde{F}_{3} )\,\overline{A}\,e^{{i(\Omega - \omega )\,T_{0} }} /2 + ( - 3\,\tilde{\beta }\,A^{2} \overline{A} - i\,\tilde{\delta }\,\omega \,A - 2\,i\omega \,D_{1} A\,)\,e^{{i\omega \,\,T_{0} }} + c.c, \\ \end{aligned}$$
(52)

and

$$(D_{0}^{2} + \omega_{1}^{2} )\,v_{1} = \tilde{q}_{2} \,A\,e^{{i\omega \,T_{0} }} + ( - i\,\tilde{\delta }_{1} \,\omega_{1} B - 2\,i\omega_{1} \,D_{1} B\,)\,e^{{i\omega_{1} T_{0} }} + c.c.$$
(53)

where \(c.c\) signifies the complex conjugates of the previous terms.

To this end, the purpose of the study is to reduce the vibration of the considered prototype. Consequently, the non-resonance case will be omitted. So, the following investigation focuses only on the resonance cases. It should be noticed that the resonance cases must be determined for Eqs. (52) and (53), namely, the primary resonance (\(\Omega = \omega\)) and the internal resonance (\(\omega_{1} = \omega\)). Subsequently, the detuning parameters \(\sigma_{1}\) and \(\sigma_{2}\) as a closeness to the described frequencies are assumed as follows:

$$\Omega = \omega + \sigma_{1} = \omega + \varepsilon \,\tilde{\sigma }_{1} ,\quad \omega_{1} = \omega + \sigma_{2} = \omega + \varepsilon \,\tilde{\sigma }_{2} .$$
(54)

Substituting Eq. (54) into Eqs. (52) and (53), the solvability conditions may be formulated as:

$$2\,i\omega \,D_{1} A = - i\,\tilde{F}_{1} \,e^{{i\,\,\tilde{\sigma }_{1} \,T_{1} }} /2 + \tilde{q}_{1} \,B\,e^{{i\,\tilde{\sigma }_{2} T_{1} }} - 3\,\tilde{\beta }\,A^{2} \overline{A} - i\,\tilde{\delta }\,\omega \,A,$$
(55)

and

$$2\,i\omega_{1} \,D_{1} B = \tilde{q}_{2} \,A\,e^{{ - i\,\tilde{\sigma }_{2} \,T_{1} }} - i\,\tilde{\delta }_{1} \,\omega_{1} B.$$
(56)

Consequently, the specific solutions of Eqs. (52) and (53), after removing the terms of the secular terms, become

$$\theta_{1} = \left[ {\frac{{\tilde{\beta }\,A^{3} }}{{8\,\omega^{2} }}} \right]\,e^{{3i\omega \,\,T_{0} }} + \,\left[ {\frac{{( - \tilde{F}_{2} \, + i\tilde{F}_{3} )\,\overline{A}}}{{2\,\left( {\omega^{2} - \,(\Omega - \omega )^{2} } \right)}}} \right]e^{{i(\Omega - \omega )\,T_{0} }} + \left[ {\frac{{( - \tilde{F}_{2} \, + i\tilde{F}_{3} )A}}{{2\,\left( {\omega^{2} - \,(\Omega + \omega )^{2} } \right)}}} \right]e^{{i(\omega + \Omega )\,T_{0} }} + c.c,$$
(57)

and

$$v_{1} = 0.$$
(58)

Again, Substituting Eqs. (50), (51), (57) and (58) into Eqs. (48) and (49), the second order equations may be reduced to the following equations:

$$\begin{aligned} (D_{0}^{2} + \omega^{2} )\,\theta_{2} & = \theta_{25} \,e^{{i\omega T_{0} }} + \theta_{26} \,e^{{3\,i\omega \,\,T_{0} }} + \theta_{27} \,e^{{5i\omega \,\,T_{0} }} + \theta_{28} \,e^{{i(\Omega + \omega )\,\,T_{0} }} + \theta_{29} \,e^{{i(\Omega - \omega )\,\,T_{0} }} \\ & \,\,\,\,\,\, + \theta_{30} \,e^{{i(\Omega + 3\omega )\,\,T_{0} }} + \theta_{31} \,e^{{i(\Omega - 3\omega )\,\,T_{0} }} + \theta_{32} \,e^{{i(2\,\Omega + \omega )\,\,T_{0} }} + \theta_{33} \,e^{{i(2\,\Omega - \omega )\,\,T_{0} }} + c.c, \\ \end{aligned}$$
(59)

and

$$(D_{0}^{2} + \omega_{1}^{2} )\,v_{2} = \theta_{34} \,e^{{i(\Omega - \omega )\,T_{0} }} + \theta_{35} \,e^{{i(\omega + \Omega )\,T_{0} }} + \theta_{36} \,e^{{3i\omega \,T_{0} }} + \theta_{37} \,e^{{i\omega_{1} T_{0} }} + c.c.$$
(60)

where \(\theta_{ij}\) are given in the Appendix to follow the paper easily.

Once more, the solvability condition for Eqs. (59) and (60) is

$$2i\omega \,D_{2} A = \frac{{ - 3\,\,\tilde{\beta }^{2} \,A^{3} \,\overline{A}^{2} }}{{8\,\omega^{2} }} + \frac{{A\,(\tilde{F}_{2}^{2} \, + \tilde{F}_{3}^{2} )}}{{4\,(\omega^{2} - (\Omega + \omega )^{2} )}} + \frac{{A\,(\tilde{F}_{2}^{2} \, + \tilde{F}_{3}^{2} )}}{{4\,(\omega^{2} - (\Omega - \omega )^{2} )}} - \tilde{\delta }\,D_{1} A - D_{1}^{2} + \frac{{\overline{A}(\tilde{F}_{2} - i\,\tilde{F}_{3} )^{2} }}{{4\,(\omega^{2} - (\Omega - \omega )^{2} )}}\,e^{{2\,i\,\tilde{\sigma }_{1} \,T_{1} }} ,$$
(61)

and

$$2\,i\omega_{1} \,D_{2} B = - \tilde{\delta }_{1} \,D_{1} B - \,D_{1}^{2} B.$$
(62)

Consequently, the solutions of Eqs. (59) and (60) after removing the secular terms are

$$\begin{aligned} \theta_{2} & = \frac{{ - \,\theta_{26} }}{{8\,\omega^{2} }}\,e^{{3\,i\omega \,\,T_{0} }} - \frac{{\theta_{27} }}{{24\,\omega^{2} }}\,e^{{5i\omega \,\,T_{0} }} + \frac{{\theta_{28} }}{{(\omega^{2} - (\Omega + \omega )^{2} )}}\,e^{{i(\Omega + \omega )\,\,T_{0} }} + \frac{{\theta_{29} }}{{(\omega^{2} - (\Omega - \omega )^{2} )}}\,e^{{i(\Omega - \omega )\,\,T_{0} }} \\ & \,\,\, + \frac{{\theta_{30} }}{{(\omega^{2} - (\Omega + 3\,\omega )^{2} )}}\,e^{{i(\Omega + 3\omega )\,\,T_{0} }} + \frac{{\theta_{31} }}{{(\omega^{2} - (\Omega - 3\,\omega )^{2} )}}\,e^{{i(\Omega - 3\omega )\,\,T_{0} }} + \frac{{\theta_{32} }}{{(\omega^{2} - (2\,\Omega + \omega )^{2} )}}\,e^{{i(2\,\Omega + \omega )\,\,T_{0} }} + c.c, \\ \end{aligned}$$
(63)

and

$$v_{2} = \frac{{\theta_{34} }}{{(\omega_{1}^{2} - (\Omega - \omega )^{2} )}}\,e^{{i(\Omega - \omega )\,T_{0} }} + \frac{{\theta_{35} }}{{(\omega_{1}^{2} - (\Omega + \omega )^{2} )}}\,e^{{i(\omega + \Omega )\,T_{0} }} + \frac{{\theta_{34} }}{{(\omega_{1}^{2} - 9\,\omega^{2} )}}\,e^{{3i\omega \,T_{0} }} + c.c.$$
(64)

The general approximate solution of Eqs. (38) and (39) can be obtained by exchanging Eqs. (50), (51), (57), (58), (63) and (64) into Eqs. (40)-(41). Additionally, in the next section, we will study the stability of the measured resonance case.

Linearized stability of the non-autonomous equation

Considering Eq. (42), the combinations of Eqs. (55) and (61), then Eqs. (56) and (62) yield the following equations:

$$\begin{aligned} 2\,i\omega \,\frac{dA}{{d\,t}} & = \varepsilon \,\left( { - i\,\tilde{F}_{1} \,e^{{i\,\,\tilde{\sigma }_{1} \,T_{1} }} /2 + \tilde{q}_{1} \,B\,e^{{i\,\tilde{\sigma }_{2} T_{1} }} - 3\,\tilde{\beta }\,A^{2} \overline{A} - i\,\tilde{\delta }\,\omega \,A) + \varepsilon^{2} \,\left\{ {\frac{{ - 3\,\,\tilde{\beta }^{2} \,A^{3} \,\overline{A}^{2} }}{{8\,\omega^{2} }} + \frac{{A\,(\tilde{F}_{2}^{2} \, + \tilde{F}_{3}^{2} )}}{{4\,(\omega^{2} - (\Omega + \omega )^{2} )}}} \right.} \right. \\ & \,\,\,\,\,\,\,\,\, + \left. {\frac{{A\,(\tilde{F}_{2}^{2} \, + \tilde{F}_{3}^{2} )}}{{4\,(\omega^{2} - (\Omega - \omega )^{2} )}}} \right) - \tilde{\delta }\,\left( {\frac{{ - \tilde{F}_{1} \,e^{{i\,\,\tilde{\sigma }_{1} \,T_{1} }} }}{4\,\omega } - \frac{{i\,\tilde{q}_{1} \,B}}{2\,\omega }\,e^{{i\,\tilde{\sigma }_{2} T_{1} }} + \frac{{3\,i\,\tilde{\beta }\,A^{2} \overline{A}}}{2\,\omega } - \frac{{\,\tilde{\delta }\,A}}{2\,}} \right) - \left( {\frac{{\tilde{\delta }^{2} \,A}}{4\,} - \frac{{3\,i\,\tilde{\delta }\,\tilde{\beta }\,A^{2} \,\overline{A}}}{\omega }} \right. \\ & \,\,\,\,\,\,\,\,\, - \frac{{9\,\tilde{\beta }^{2} \,A^{3} \,\overline{A}^{2} }}{{4\,\omega^{2} }} - \frac{{\tilde{q}_{1} \,\tilde{q}_{2} \,A}}{{4\,\omega \,\omega_{1} }} + \left( {\frac{{\tilde{\delta }\,\tilde{F}_{1} }}{8\,\omega } - \frac{{3\,i\,\tilde{\beta }\,\tilde{F}_{1} \,A\,\overline{A}}}{{4\,\omega^{2} }} - \frac{{i\,\tilde{F}_{1} \,\tilde{\sigma }_{1} }}{4\,\omega }} \right)\,e^{{i\,\,\tilde{\sigma }_{1} \,T_{1} }} + \left( {\frac{{i\,\tilde{q}_{1} \,B\,(\tilde{\delta } + \tilde{\delta }_{1} )}}{4\,\omega } + \frac{{3\,\tilde{\beta }\,\tilde{q}_{1} \,B\,A\,\overline{A}}}{{2\,\omega^{2} }}} \right. \\ & \,\,\,\,\,\,\,\,\, + \left. {\left. {\frac{{\tilde{q}_{1} \,\tilde{\sigma }_{2} \,B}}{2\,\omega }} \right)e^{{i\,\tilde{\sigma }_{2} T_{1} }} - \left( {\frac{{3\,i\,\tilde{\beta }\,\tilde{F}_{1} \,A^{2} }}{{8\,\omega^{2} }}} \right)\,e^{{ - i\,\,\tilde{\sigma }_{1} \,T_{1} }} - \left. {\left( {\frac{{3\,\tilde{\beta }\,\tilde{q}_{1} \,\overline{B}\,A^{2} }}{{4\,\omega^{2} }}} \right)\,e^{{ - i\,\,\tilde{\sigma }_{2} \,T_{1} }} } \right) + \frac{{\overline{A}(\tilde{F}_{2} - i\,\tilde{F}_{3} )^{2} }}{{4\,(\omega^{2} - (\Omega - \omega )^{2} )}}\,e^{{2\,i\,\tilde{\sigma }_{1} \,T_{1} }} } \right\}, \\ \end{aligned}$$
(65)

and

$$\begin{aligned} 2\,i\omega_{1} \,\frac{dB}{{d\,t}} & = \varepsilon \left( {\tilde{q}_{2} \,A\,e^{{ - i\,\,\sigma_{2} \,T_{1} }} - i\,\tilde{\delta }_{1} \,\omega_{1} B) + \,\varepsilon^{2} \left\{ { - \tilde{\delta }_{1} \,\left( {\frac{{ - i\,\tilde{q}_{2} \,A}}{{2\,\omega_{1} }}\,e^{{ - i\,\tilde{\sigma }_{2} \,T_{1} }} - \frac{{\tilde{\delta }_{1} \,}}{2\,}B} \right) - \left( {\frac{{\tilde{\delta }_{1}^{2} \,B}}{4} - \frac{{\tilde{q}_{1} \,\tilde{q}_{2} \,B}}{4\,\omega \,\omega }} \right.} \right.} \right. \\ & \,\,\,\,\, + \left. {\left. {\left( {\frac{{i\,\tilde{q}_{2} \,(\tilde{\delta } + \tilde{\delta }_{1} )\,A}}{{4\,\omega_{1} }} + \frac{{3\,\tilde{q}_{2} \,\tilde{\beta }\,A^{2} \,\overline{A}}}{{4\,\omega \,\omega_{1} }} - \frac{{\tilde{\sigma }_{2} \,\tilde{q}_{2} \,A}}{{2\,\omega_{1} }}} \right)\,e^{{ - i\,\tilde{\sigma }_{2} \,T_{1} }} + \frac{{i\,\tilde{q}_{2} \,\tilde{F}_{1} }}{{8\,\omega \,\omega_{1} }}e^{{i\,(\tilde{\sigma }_{1} - \tilde{\sigma }_{2} )\,T_{1} }} } \right)} \right\}. \\ \end{aligned}$$
(66)

The coupled system of Eqs. (65) and (66) is first order nonlinear ordinary differential equations of \(A\) and \(B\) of complex coefficients. To study the solution of Eqs. (65) and (66), it is appropriate to use the polar form for the complex functions \(A(T_{1} ,T_{2} )\) and \(B(T_{1} ,T_{2} )\) as:

$$A = \frac{{\tilde{a}_{1} }}{2}e^{{i\rho_{1} }} \quad {\text{and}}\quad B = \frac{{\tilde{a}_{2} }}{2}e^{{i\rho_{2} }} ,$$
(67)

where \(\,\tilde{a}_{1} ,\,\,\,\tilde{a}_{2} ,\,\,\rho_{1}\) and \(\,\,\rho_{2}\) are real functions on the time \(\,\,t\).

We may investigate these functions as \(a_{1} = \varepsilon \,\tilde{a}_{1}\), \(a_{2} = \varepsilon \,\tilde{a}_{2}\).The direct differentiation of the previous functions provides

$$\dot{A} = \frac{{\dot{\tilde{a}}_{1} }}{2}e^{{i\rho_{1} }} + i\frac{{\tilde{a}_{1} }}{2}\dot{\rho }_{1} e^{{i\rho_{1} }} \quad {\text{and}}\quad \dot{B} = \frac{{\dot{\tilde{a}}_{2} }}{2}e^{{i\rho_{2} }} + i\frac{{\tilde{a}_{2} }}{2}\dot{\rho }_{2} e^{{i\rho_{2} }} .$$
(68)

Using Eqs. (67) and (68) into Eqs. (65) and (66), with the restoration of each scaled factor to its basic form, then distinguishing the real and imaginary elements yield the following

$$\begin{aligned} \dot{a}_{1} & = - \frac{\delta }{2}a_{1} + \frac{3\beta \,\delta }{{16\,\omega^{2} }}a_{1}^{3} + \frac{{F_{1} \,(9\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{1} - 2\omega ))}}{{32\,\omega^{3} }}\cos \psi_{1} + \frac{{\,\delta \,F_{1} }}{{8\,\omega^{2} }}\,\sin \psi_{1} + \frac{{q_{1} \,(\delta - \,\delta_{1} )}}{{8\,\omega^{2} }}a_{2} \,\cos \psi_{2} \\ & \,\,\,\,\, + \frac{{q_{1} \,( - 9\beta \,a_{1}^{2} + 8\,\omega \,( - \sigma_{2} + 2\omega ))}}{{32\,\omega^{3} }}\,a_{2} \,\sin \psi_{2} - \frac{{F_{2} \,F_{3} }}{4\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\cos 2\,\psi_{1} + \frac{{(F_{2}^{2} - F_{3}^{2} )}}{8\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\sin 2\,\psi_{1} , \\ \end{aligned}$$
(69)
$$\begin{aligned} a_{1} \,\dot{\rho }_{1} & = - \frac{{\delta^{2} }}{8\,\omega }\,a_{1} - \frac{{q_{1} \,q_{2} }}{{8\,\omega_{1} \,\omega^{2} }}\,a_{1} + \frac{3\,\beta }{{8\,\omega }}\,a_{1}^{3} - \frac{{15\,\beta^{2} }}{{256\,\omega^{3} }}\,a_{1}^{5} - \frac{{(\,F_{2}^{2} + F_{3}^{2} )}}{4\,\omega \,(2\,\omega - \Omega )\,(2\,\omega + \Omega )}\,a_{1} - \frac{{\delta \,F_{1} }}{{8\,\omega^{2} }}\,\cos \psi_{1} \\ & \,\,\,\,\,\,\,\,\,\, + \frac{{F_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{1} - 2\omega ))}}{{32\,\omega^{3} }}\sin \psi_{1} - \frac{{(F_{2}^{2} \, - F_{3}^{2} )}}{8\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\cos 2\,\psi_{1} - \frac{{F_{2} \,F_{3} }}{4\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\sin 2\psi_{1} \\ & \,\,\,\,\,\,\,\,\,\, + \frac{{q_{1} \,(\delta - \,\delta_{1} )}}{{8\,\omega^{2} }}a_{2} \,\sin \psi_{2} + \frac{{q_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{2} - 2\omega ))}}{{32\,\omega^{3} }}\,a_{2} \,\cos \psi_{2} , \\ \end{aligned}$$
(70)
$$\dot{a}_{2} = - \frac{1}{2}\,\delta_{1} \,a_{2} - \frac{{q_{2} (\delta - \,\delta_{1} )}}{{8\,\omega_{1}^{2} }}\,a_{1} \,\cos \psi_{2} + \frac{{q_{2} (3\beta \,a_{1}^{2} - 8\omega \,\sigma_{2} - 16\,\omega \,\omega_{1} )}}{{32\,\omega \,\omega_{1}^{2} }}\,a_{1} \,\sin \psi_{2} - \frac{{F_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} }}\,\cos (\psi_{1} - \psi_{2} ),$$
(71)
$$\begin{aligned} a_{2} \,\dot{\rho }_{2} & = - \frac{{q_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} }}\,a_{2} - \frac{{\delta_{1}^{2} }}{{8\,\omega_{1} }}\,a_{2} + \frac{{q_{2} (\delta - \,\delta_{1} )}}{{8\,\omega_{1}^{2} }}\,a_{1} \,\sin \psi_{2} + \frac{{q_{2} (3\,\beta \,a_{1}^{2} - 8\,\omega \,\sigma_{2} - 16\,\omega \,\omega_{1} )}}{{32\,\omega \,\omega_{1}^{2} }}\,a_{1} \,\cos \psi_{2} \\ & \,\,\,\,\,\,\,\,\,\,\,\, - \frac{{F_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} }}\,\sin (\psi_{1} - \psi_{2} ). \\ \end{aligned}$$
(72)

where \(\psi_{1} = \sigma_{1} t - \rho_{1}\) and \(\psi_{2} = \sigma_{2} t - \rho_{1} + \rho_{2}\), therefore \(\dot{\psi }_{1} = \sigma_{1} - \dot{\rho }_{1}\) and \(\dot{\psi }_{2} = \sigma_{2} - \dot{\rho }_{1} + \dot{\rho }_{2} = \sigma_{2} - \sigma_{1} + \dot{\psi }_{1} + \dot{\rho }_{2}\), one finds

$$\begin{aligned} \dot{\psi }_{1} & = \sigma_{1} + \frac{{\delta^{2} }}{8\,\omega } + \frac{{q_{1} \,q_{2} }}{{8\,\omega_{1} \,\omega^{2} }} - \frac{3\,\beta }{{8\,\omega }}\,a_{1}^{2} + \frac{{15\,\beta^{2} }}{{256\,\omega^{3} }}\,a_{1}^{4} + \frac{{(\,F_{2}^{2} + F_{3}^{2} )}}{4\,\omega \,(2\,\omega - \Omega )\,(2\,\omega + \Omega )} \\ &\quad- \frac{{F_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{1} - 2\omega ))}}{{32\,\omega^{3} \,a_{1} }}\sin \psi_{1} + \frac{{\delta \,F_{1} }}{{8\,\omega^{2} \,a_{1} }}\,\cos \psi_{1} \\ &\quad + \frac{{(F_{2}^{2} \, - F_{3}^{2} )}}{8\,\omega \,\Omega \,(2\,\omega - \Omega )}\,\cos 2\psi_{1} + \frac{{F_{2} \,F_{3} }}{4\,\omega \,\Omega \,(2\,\omega - \Omega )}\,\sin 2\psi_{1} \\ &\quad- \frac{{q_{1} \,(\delta - \,\delta_{1} )}}{{8\,\omega^{2} }}\,\frac{{a_{2} }}{{a_{1} }}\,\sin \psi_{1} \, - \frac{{q_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{2} - 2\omega ))}}{{32\,\omega^{3} }}\,\frac{{a_{2} }}{{a_{1} }}\,\cos \psi_{2} \\ \end{aligned}$$
(73)
$$\begin{aligned} \dot{\psi }_{2} & = \sigma_{2} + \frac{{\delta^{2} }}{8\,\omega } + \frac{{q_{1} \,q_{2} }}{{8\,\omega_{1} \,\omega^{2} }} - \frac{3\,\beta }{{8\,\omega }}\,a_{1}^{2} + \frac{{15\,\beta^{2} }}{{256\,\omega^{3} }}\,a_{1}^{4} + \frac{{(\,F_{2}^{2} + F_{3}^{2} )}}{4\,\omega \,(2\,\omega - \Omega )\,(2\,\omega + \Omega )} \\ &\quad- \frac{{F_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{1} - 2\omega ))}}{{32\,\omega^{3} \,a_{1} }}\sin \psi_{1} + \frac{{\delta \,F_{1} }}{{8\,\omega^{2} \,a_{1} }}\,\cos \psi_{1} + \frac{{(F_{2}^{2} \, - F_{3}^{2} )}}{8\,\omega \,\Omega \,(2\,\omega - \Omega )}\,\cos 2\,\psi_{1} \\ & \quad + \frac{{F_{2} \,F_{3} }}{4\,\omega \,\Omega \,(2\,\omega - \Omega )}\,\sin 2\,\psi_{1} - \frac{{q_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{2} - 2\omega ))}}{{32\,\omega^{3} }}\,\frac{{a_{2} }}{{a_{1} }}\,\cos \psi_{2} - \frac{{q_{1} \,(\delta - \,\delta_{1} )}}{{8\,\omega^{2} }}\,\frac{{a_{2} }}{{a_{1} }}\,\sin \psi_{2} \\ & \,\,\,\,\,\, - \frac{{q_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} }} - \frac{{\delta_{1}^{2} }}{{8\,\omega_{1} }} + \frac{{q_{2} (\delta - \,\delta_{1} )}}{{8\,\omega_{1}^{2} }}\,\frac{{a_{1} }}{{a_{2} }}\,\sin \psi_{2} + \frac{{q_{2} (3\,\beta \,a_{1}^{2} - 8\,\omega \,\sigma_{2} - 16\,\omega \,\omega_{1} )}}{{32\,\omega \,\omega_{1}^{2} }}\,\frac{{a_{1} }}{{a_{2} }}\,\cos \psi_{2} \\ & \quad - \frac{{F_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} \,a_{2} }}\,\sin (\psi_{1} - \psi_{2} ) \\ \end{aligned}$$
(74)

Equations (69), (71), (73) and (74) are defined as autonomous amplitude-phase modulating equations. We will use these equations to investigate the linearized stability in case of the presence of periodic fields in the governing equation of IP before adding the controller (i.e. putting \(a_{2} = 0\), \(\psi_{2} = 0\)). The following procedure comes out from He et al.17 and Hao et al.33. For this purpose, Eqs. (69) and (73) are used and the following assumptions are considered:

$$\dot{a}_{1} = f(a_{1} ,\psi_{1} ),\quad a_{1} \,\dot{\psi }_{1} = u(a_{1} ,\psi_{1} ).$$
(75)

The critical points are determined from the following equations:

$$f(a_{1} ,\psi_{1} ) = 0,\quad u(a_{1} ,\psi_{1} ) = 0,$$
(76)

Here, the Jacobian matrix is defined as

$$\Gamma = \left( {\begin{array}{*{20}c} {\frac{\partial f}{{\partial a_{1} }}} & {\frac{\partial f}{{\partial \psi_{1} }}} \\ {\frac{\partial u}{{\partial a_{1} }}} & {\frac{\partial u}{{\partial \psi_{1} }}} \\ \end{array} } \right).$$
(77)

The eigenvalues \(\Lambda_{r}\), (\(r = 1,\,2\)) are given from the characteristic equation \(\Gamma - \Lambda_{r} \,I_{2 \times 2} = 0\). Actually, the use of the Mathematica software 13.0.0.0 yields several characteristic values. They are not included here to keep the paper from getting too long. Additionally, in our earlier work29, a characterization of the connection between the nature of these roots and the various forms of stability was provided. Table 2 offers a review of the results of the previous operations with regard to various amounts of the system factors.

Table 2 Equilibria classification of the eigenvalues and their stability/instability.
Full size table
Figure 11
figure 11

Phase portrait at \(\delta = 0.02\).

Full size image
Figure 12
figure 12

Phase portrait at \(\omega = 0.2\).

Full size image
Figure 13
figure 13

Phase portrait at \(\delta = 0.3\).

Full size image
Figure 14
figure 14

Phase portrait at \(\delta = - \,0.3\).

Full size image
Figure 15
figure 15

Phase portrait at \(F_{1} = 5\).

Full size image
Figure 16
figure 16

Phase portrait at \(F_{3} = 2\).

Full size image

For more convenience, the corresponding phase portraits are shown below.

Linearized stability of the non-autonomous system

The steady-state solution of the system through the PPF controller associated to the fixed point of as given in Eqs. (69)–(72) is achieved by considering \(\dot{a}_{m} = 0\), and \(\dot{\psi }_{m} = 0\),\((m = 1,\,2)\). Therefore, the FREs of the existing case (\(a_{1} \ne 0,a_{2} \ne 0\)) are given by solving the following algebraic equations:

$$\begin{aligned} 0 & = - \frac{\delta }{2}a_{1} + \frac{3\beta \,\delta }{{16\,\omega^{2} }}a_{1}^{3} + \frac{{F_{1} \,(9\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{1} - 2\omega ))}}{{32\,\omega^{3} }}\cos \psi_{1} + \frac{{\,\delta \,F_{1} }}{{8\,\omega^{2} }}\,\sin \psi_{1} + \frac{{q_{1} \,(\delta - \,\delta_{1} )}}{{8\,\omega^{2} }}a_{2} \,\cos \psi_{2} \\ & \quad \, + \frac{{q_{1} \,( - 9\beta \,a_{1}^{2} + 8\,\omega \,( - \sigma_{2} + 2\omega ))}}{{32\,\omega^{3} }}\,a_{2} \,\sin \psi_{2} - \frac{{F_{2} \,F_{3} }}{4\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\cos 2\,\psi_{1} + \frac{{(F_{2}^{2} - F_{3}^{2} )}}{8\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\sin 2\,\psi_{1} , \\ \end{aligned}$$
(78)
$$\begin{aligned} \sigma_{1} \,a_{1} & = - \frac{{\delta^{2} }}{8\,\omega }\,a_{1} - \frac{{q_{1} \,q_{2} }}{{8\,\omega_{1} \,\omega^{2} }}\,a_{1} + \frac{3\,\beta }{{8\,\omega }}\,a_{1}^{3} - \frac{{15\,\beta^{2} }}{{256\,\omega^{3} }}\,a_{1}^{5} - \frac{{(\,F_{2}^{2} + F_{3}^{2} )}}{4\,\omega \,(2\,\omega - \Omega )\,(2\,\omega + \Omega )}\,a_{1} - \frac{{\delta \,F_{1} }}{{8\,\omega^{2} }}\,\cos \,\psi_{1} \\ & \,\,\,\,\,\,\,\,\,\, + \frac{{F_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{1} - 2\omega ))}}{{32\,\omega^{3} }}\sin \psi_{1} - \frac{{(F_{2}^{2} \, - F_{3}^{2} )}}{8\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\cos 2\,\psi_{1} - \frac{{F_{2} \,F_{3} }}{4\,\omega \,\Omega \,(2\,\omega - \Omega )}\,a_{1} \,\sin 2\psi_{1} \\ & \,\,\,\,\,\,\,\,\,\, + \frac{{q_{1} \,(\delta - \,\delta_{1} )}}{{8\,\omega^{2} }}a_{2} \,\sin \psi_{2} + \frac{{q_{1} \,(3\beta \,a_{1}^{2} + 8\,\omega \,(\sigma_{2} - 2\omega ))}}{{32\,\omega^{3} }}\,a_{2} \,\cos \psi_{2} , \\ \end{aligned}$$
(79)
$$0 = - \frac{1}{2}\,\delta_{1} \,a_{2} - \frac{{q_{2} (\delta - \,\delta_{1} )}}{{8\,\omega_{1}^{2} }}\,a_{1} \,\cos \psi_{2} + \frac{{q_{2} (3\beta \,a_{1}^{2} - 8\omega \,\sigma_{2} - 16\,\omega \,\omega_{1} )}}{{32\,\omega \,\omega_{1}^{2} }}\,a_{1} \,\sin \psi_{2} - \frac{{F_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} }}\,\cos (\psi_{1} - \psi_{2} ),$$
(80)
$$\begin{aligned} (\sigma_{1} - \sigma_{2} )\,a_{2} & = - \frac{{q_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} }}\,a_{2} - \frac{{\delta_{1}^{2} }}{{8\,\omega_{1} }}\,a_{2} + \frac{{q_{2} (\delta - \,\delta_{1} )}}{{8\,\omega_{1}^{2} }}\,a_{1} \,\sin \psi_{2} + \frac{{q_{2} (3\,\beta \,a_{1}^{2} - 8\,\omega \,\sigma_{2} - 16\,\omega \,\omega_{1} )}}{{32\,\omega \,\omega_{1}^{2} }}\,a_{1} \,\cos \psi_{2} \\ & \,\,\,\,\,\,\, - \frac{{F_{1} \,q_{2} }}{{8\,\omega \,\omega_{1}^{2} }}\,\sin (\psi_{1} - \psi_{2} ). \\ \end{aligned}$$
(81)

To construct the stability configuration of the steady-state solution, consider the following expectations:

$$a_{m} = a_{m\,0} + a_{m\,1} ,\quad \psi_{m} = \psi_{m\,0} + \psi_{m\,1} ,\quad (m = 1,\,2),$$
(82)

where \(a_{m\,0}\) and \(\psi_{m\,0}\) are the solutions of Eqs. (69), (71), (73) and (74), and the very small, perturbed quantities are defined by \(\psi_{m1}\), and \(a_{m1}\). Substituting from Eq. (82) into Eqs. (69), (71), (73) and (74), then keeping only the linear terms of \(a_{m\,1}\) and \(\psi_{m\,1}\), one gets the following matrix equation:

$$\left[ {\begin{array}{*{20}c} {\dot{a}_{11} } \\ {\dot{\psi }_{11} } \\ {\dot{a}_{21} } \\ {\dot{\psi }_{21} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {r_{11} } & {r_{12} } & {r_{13} } & {r_{14} } \\ {r_{21} } & {r_{22} } & {r_{23} } & {r_{24} } \\ {r_{31} } & {r_{32} } & {r_{33} } & {r_{34} } \\ {r_{41} } & {r_{42} } & {r_{43} } & {r_{44} } \\ \end{array} } \right]\,\left[ {\begin{array}{*{20}c} {a_{11} } \\ {\psi_{11} } \\ {a_{21} } \\ {\psi_{21} } \\ \end{array} } \right],$$
(83)

where the above square matrix is called the Jacobian matrix \({\rm X}\). The coefficients values \(r_{i\,j}\), (\(i,j = 1,2,3,4\)) are listed in the Appendix. Therefore, the eigenvalues \(\gamma_{r}\), (\(r = 1,2,3,4\)) are given by \({\rm X} - \gamma_{r} \,I_{4 \times 4} = 0\) and lead to the following equation:

$$\gamma^{4} + R_{1} \,\gamma^{3} + R_{2} \,\gamma^{2} + R_{3} \,\gamma + R_{4} = 0,$$
(84)

where the coefficients \(R_{1}\),\(R_{2}\), \(R_{3}\) and \(R_{4}\) are known from the context. In light of the Routh–Hurwitz criterion28, if the real part of the eigenvalue is negative, then the periodic solution is stable; otherwise, it is unstable.

Results and discussions

Frequency response curve (FRC) and effect of different factors

In the following Figs. 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 and 27, it should be noted that the thick curves refer to the stable regions. Otherwise, the thin ones represent the unstable regions.

Figure 17
figure 17

FRC comparison between a controlled system and an uncontrolled system.

Full size image
Figure 18
figure 18

FRC of PPF controlled system ( stable r region), ( unstable region) at σ2 (a) (a1 against σ1) and (b) (a2 against σ2)

Full size image
Figure 19
figure 19

Effects of \(\delta\) on FRC.

Full size image
Figure 20
figure 20

Effects of \(\delta_{1}\) on FRC.

Full size image
Figure 21
figure 21

Effects of \(\beta\) on FRC.

Full size image
Figure 22
figure 22

Effects of \(\omega\) on FRC.

Full size image
Figure 23
figure 23

Effects of \(\sigma_2\) on FRC.

Full size image
Figure 24
figure 24

Effects of \(F_1\) on FRC.

Full size image
Figure 25
figure 25

Effects of \(q_1\) on FRC.

Full size image
Figure 26
figure 26

Effects of \(q_2\) on FRC.

Full size image
Figure 27
figure 27

FRC comparison between both RK-4 ( ) and analytic solution ( ).

Full size image

To clarify the importance of adding the control, we make a comparison between the FRC for the system before and after adding the controller as represented in the Fig. 17. From this comparison, at the region near to \(\sigma_{1} = 0\), the steady-state amplitude for the uncontrolled structure is very high as indicated by the black curve. In the same region, the amplitude of the system after adding PPF control decreases completely as indicated by the red curve. This demonstrates the quality of the controller in reducing the vibration at the considered resonance situation. Consequently, when adding the controller, the area around \(\sigma_{1} = 0\) is called the vibration bandwidth region because it is located between two peaks as shown earlier17,34.

The steady-state solution of the model FREs, as given by Eqs. (78)–(81), is described by plotting the FRC at the current case (\(a_{1} \ne 0\),\(a_{2} \ne 0\)) as shown in Fig. 18. For this purpose, Fig. 18a displays the amplitude model \(a_{1}\) versus \(\sigma_{1}\). Simultaneously, Fig. 18b depicts the controller amplitude \(a_{2}\) versus \(\sigma_{1}\). Moreover, from Fig. 18a it appears that the vibrations after being connected to the PPF controller are damped in the region of the frequency bandwidth. Consequently, we can say that the optimal mode of vibration reduction is \(\sigma_{1} = \sigma_{2} = 0\). Earlier examples were included21,34.

Figure 19 illustrates the effects of various amounts of \(\delta\) on the FRC. When the values of \(\delta\) have increased, the amplitude of the structure has increased around the region \(\sigma_{1} = 0\). This is called the jump phenomenon, which was displayed earlier35,36. Additionally, the areas of instability and the heights of the two peaks are decreased.

By improving the amounts of \(\delta_{1}\), the bandwidth region in Fig. 20a,b are expanded. Moreover, the height of the left peak as well as the instability regions decrease. Finally, the jump phenomenon of the controller decreases as indicated in Fig. 20b. Examples from the previous phenomenon were included in17.

From Fig. 21, it is clear that as the values of \(\beta\) increase, the amplitude decreases, and the right peak is more bent to the right. Instances from the earlier occurrence were provided earlier29.

Figure 22 shows that when the \(\omega\)-values decrease, the bandwidth region expands, and the regions of instability increase. Additionally, the height of the left peak increases, while the right peak gradually continues to bend to the right. Examples from the first incident were given earlier in17,21.

When changing the values of \(\sigma_{2}\) as shown in Fig. 23, we note that the lowest values of the steady-state amplitude of the IP occur at \(\sigma_{2} = \sigma_{1}\). This establishes that the vibration has been damped at the resonance case. There have already been examples provided from the first instance17.

Figure 24 depicts the change of the different values of \(F_{1}\) on the FRC curve. It is found that the higher amounts of \(F_{1}\) produces the higher amounts of the amplitude and vice-versa for the bandwidth area. Illustrations from the previous situation were already supplied34. Therefore, the presence of the magnetic field suppresses the instability of the system.

In what follows, the influences of the parameters \(q_{1}\) and \(q_{2}\) on the curve FRC will be discussed throughout Figs. 25 and 26. The bandwidth region expands and the left peak goes up when the value of \(q_{1}\) and \(q_{2}\) are enhanced as displayed in Figs. 25a and 26a. Simultaneously, in Figs. 25b and 26b, the left peak decrease down with an increase of \(q_{1}\), while it grows with an increase in \(q_{2}\). Similar results were obtained earlier17,21.

In the following two figures, a comparison will be made to graphically verify the validation of the theoretical and numerical approaches. For this objective, the comparison of FRC between both analytic and numerical solutions. The solid red lines represent the former, while the blue circles represent the latter as shown in Fig. 27. Fairly good results were obtained (look Tables 3 and 4). It is shown that the analytical solution is very consistent with the numerical one. In Fig. 28, a comparison between the perturbation procedure as given in Eqs. (69), (71), (73) and (74), and the numerical simulation as described in Eqs. (38)–(39) along with the time history was performed. The blue dashed lines show the modulation of the amplitude of the generalized coordinate. Moreover, the red solid lines refer to the time history of vibrations which are simulated numerically of the solutions of the system with PPF-controller. As observed, we found acceptable harmony between numerical and analytical producers, which confirmed our solution as done in Fig. 27.

Table 3 Comparison of the obtained results between the RK-4 solution and the analytic solution in Fig. 27a.
Full size table
Table 4 Comparison of the obtained results between the RK-4 solution and the analytic solution in Fig. 27b.
Full size table

Figure 29 presents a comparison between different controllers to verify the good performance of the vibration reduction which appears in the IP without a controller described with the red line. The comparison is made with a green line for the nonlinear saturation control (NSC), and with a yellow line for the proportional derivative control (PD), and with a blue line for the PPF.

Figure 28
figure 28

Time history comparison between numerical solution ( ) and an analytic solution ( ) at \(\Omega = \omega\) and \(\omega_{1} = \omega\).

Full size image
Figure 29
figure 29

Time history comparison between different controllers.

Full size image

Conclusions

In the current work, the vibrating IP system is analyzed analytically and numerically without and with a PPF controller. The approximate solution before the PPF controller is accomplished by applying a modified HPM. A numerical method based on the RK-4 is employed to validate the prior approximate solution. Furthermore, both the phase portraits and the linearized stability are plotted. On the other side, the vibration reduction for IP model via PPF controller is proposed in one of the worst resonance cases. The MSPT technique is used for getting a second-order approximate solution of the controlled measured system. The stability analysis of the situations \(\Omega \cong \omega\) and \(\omega_{1} \cong \omega\), with the aid of the Routh–Hurwitz criterion, is examined. Moreover, a collection of drawings is made to demonstrate the FRC and different factors using the MATLAB program. The main outcomes of the whole work may be summed in the subsequent points:

  1. 1.

    For both autonomous and non-autonomous examples, phase portraiture and the linearized stability of IP near fixed locations are displayed.

  2. 2.

    The stability of IP is improved by the presence of the magnetic field.

  3. 3.

    The PPF controller is succeeded in reducing vibrations for the considered IP system with a reduced rate of 90.5%.

  4. 4.

    The amplitude of the IP system is increased as the following parameters: \(F_{1} ,\omega \,\,{\text{and}}\,\,\delta\) increase, and the bandwidth region progressively decreases for \(F_{1} ,\,\omega \,\) and progressively disappears for \(\delta\). Additionally, the unstable regions are decreased.

  5. 5.

    The increasing the values of the following parameters \(q_{1} ,q_{2} ,\beta \,\,{\text{and}}\,\,\delta_{1}\) leads to a decrease in the amplitude of the IP system progressively.

  6. 6.

    The IP system with a PPF controller is reached to the smallest values on the frequency response curve at \(\sigma_{1} = \,\sigma_{2}\).

  7. 7.

    A comparison between the analytical and the numerical scheme provides an appropriate agreement between them before and after adding the PPF controller as presented in Figs. 2 and 28.

  8. 8.

    For validation response curves, there exist great agreements between the approximation FRC and RK-4 solutions as presented in Fig. 27.

For progress works, the topic of IP can be analyzed in different situations: Concerning the approximate analytical solution, and away from the weakness of expanding the restoring forces, a relatively new methodology which is known as the He’s frequency37,38,39 can be applied. Another effective controller could be adopted like a proportional integral derivative (PID) controller or nonlinear integral positive position feedback (NIPPF) controller to decrease the high vibration amplitude of the systems in a small time.