Abstract
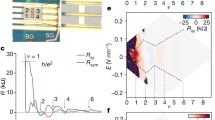
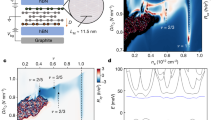
The integer quantum anomalous Hall (QAH) effect is a lattice analogue of the quantum Hall effect at zero magnetic field1,2,3. This phenomenon occurs in systems with topologically non-trivial bands and spontaneous time-reversal symmetry breaking. Discovery of its fractional counterpart in the presence of strong electron correlations, that is, the fractional QAH effect4,5,6,7, would open a new chapter in condensed matter physics. Here we report the direct observation of both integer and fractional QAH effects in electrical measurements on twisted bilayer MoTe2. At zero magnetic field, near filling factor ν = −1 (one hole per moiré unit cell), we see an integer QAH plateau in the Hall resistance Rxy quantized to h/e2 ± 0.1%, whereas the longitudinal resistance Rxx vanishes. Remarkably, at ν = −2/3 and −3/5, we see plateau features in Rxy at \(\frac{3}{2}h/{e}^{2}\pm 1 \% \) and \(\frac{5}{3}h/{e}^{2}\pm 3 \% \), respectively, whereas Rxx remains small. All features shift linearly versus applied magnetic field with slopes matching the corresponding Chern numbers −1, −2/3 and −3/5, precisely as expected for integer and fractional QAH states. Additionally, at zero magnetic field, Rxy is approximately 2h/e2 near half-filling (ν = −1/2) and varies linearly as ν is tuned. This behaviour resembles that of the composite Fermi liquid in the half-filled lowest Landau level of a two-dimensional electron gas at high magnetic field8,9,10,11,12,13,14. Direct observation of the fractional QAH and associated effects enables research in charge fractionalization and anyonic statistics at zero magnetic field.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper.
References
Chang, C.-Z., Liu, C.-X. & MacDonald, A. H. Colloquium: quantum anomalous Hall effect. Rev. Mod. Phys. 95, 011002 (2023).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 61, 2015–2018 (1988).
Sheng, D.N., Gu, Z.-C., Sun, K. & Sheng, L. Fractional quantum Hall effect in the absence of Landau levels. Nat. Commun. 2, 389 (2011).
Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011).
Tang, E., Mei, J.-W. & Wen, X.-G. High-temperature fractional quantum Hall states. Phys. Rev. Lett. 106, 236802 (2011).
Regnault, N. & Bernevig, B. A. Fractional Chern insulator. Phys. Rev. X 1, 021014 (2011).
Willett, R. et al. Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776 (1987).
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).
Halperin, B. I., Lee, P. A. & Read, N. Theory of the half-filled Landau level. Phys. Rev. B 47, 7312 (1993).
Willett, R. L., Ruel, R. R., West, K. W. & Pfeiffer, L. N. Experimental demonstration of a Fermi surface at one-half filling of the lowest Landau level. Phys. Rev. Lett. 71, 3846–3849 (1993).
Kang, W., Stormer, H. L., Pfeiffer, L. N., Baldwin, K. W. & West, K. W. How real are composite fermions? Phys. Rev. Lett. 71, 3850–3853 (1993).
Goldman, V. J., Su, B. & Jain, J. K. Detection of composite fermions by magnetic focusing. Phys. Rev. Lett. 72, 2065–2068 (1994).
Halperin, B. I. & Jain, J. K. (eds) Fractional Quantum Hall Effects: New Developments (World Scientific, 2020).
Klitzing, K. V., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559 (1982).
Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395 (1983).
Halperin, B. I. Statistics of quasiparticles and the hierarchy of fractional quantized Hall states. Phys. Rev. Lett. 52, 1583–1586 (1984).
Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723 (1984).
Zhang, S. C., Hansson, T. H. & Kivelson, S. Effective-field-theory model for the fractional quantum Hall effect. Phys. Rev. Lett. 62, 82–85 (1989).
Moore, G. & Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 360, 362–396 (1991).
Wen, X. G. Non-Abelian statistics in the fractional quantum Hall states. Phys. Rev. Lett. 66, 802–805 (1991).
Nakamura, J., Liang, S., Gardner, G. C. & Manfra, M. J. Direct observation of anyonic braiding statistics. Nat. Phys. 16, 931–936 (2020).
Bartolomei, H. et al. Fractional statistics in anyon collisions. Science 368, 173–177 (2020).
Deng, Y. et al. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 367, 895–900 (2020).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Li, T. et al. Quantum anomalous Hall effect from intertwined moiré bands. Nature 600, 641–646 (2021).
Cai, J. et al. Signatures of fractional quantum anomalous Hall states in twisted MoTe2. Nature https://doi.org/10.1038/s41586-023-06289-w (2023).
Foutty, B. A. et al. Mapping twist-tuned multi-band topology in bilayer WSe2. Preprint at https://doi.org/10.48550/arXiv.2304.09808 (2023).
Xie, Y. et al. Fractional Chern insulators in magic-angle twisted bilayer graphene. Nature 600, 439–443 (2021).
Spanton, E. M. et al. Observation of fractional Chern insulators in a van der Waals heterostructure. Science 360, 62–66 (2018).
Anderson, E. et al. Programming correlated magnetic states with gate-controlled moiré geometry. Science 381, 325–330 (2023).
Zeng, Y. et al. Thermodynamic evidence of fractional Chern insulator in moiré MoTe2. Nature https://doi.org/10.1038/s41586-023-06452-3 (2023).
Wang, C. et al. Fractional Chern insulator in twisted bilayer MoTe2. Preprint at https://doi.org/10.48550/arXiv.2304.11864 (2023).
Li, H., Kumar, U., Sun, K. & Lin, S.-Z. Spontaneous fractional Chern insulators in transition metal dichalcogenide moiré superlattices. Phys. Rev. Res. 3, L032070 (2021).
Wu, F., Lovorn, T., Tutuc, E., Martin, I. & MacDonald, A. Topological insulators in twisted transition metal dichalcogenide homobilayers. Phys. Rev. Lett. 122, 086402 (2019).
Yu, H., Chen, M. & Yao, W. Giant magnetic field from moiré induced Berry phase in homobilayer semiconductors. Natl Sci. Rev. 7, 12–20 (2020).
Zhang, Y.-H., Mao, D., Cao, Y., Jarillo-Herrero, P. & Senthil, T. Nearly flat Chern bands in moiré superlattices. Phys. Rev. B 99, 075127 (2019).
Devakul, T., Crépel, V., Zhang, Y. & Fu, L. Magic in twisted transition metal dichalcogenide bilayers. Nat. Commun. 12, 6730 (2021).
Reddy, A. P., Alsallom, F. F., Zhang, Y., Devakul, T. & Fu, L. Fractional quantum anomalous Hall states in twisted bilayer MoTe2 and WSe2. Phys. Rev. B 108, 085117 (2023).
Crépel, V. & Fu, L. Anomalous Hall metal and fractional Chern insulator in twisted transition metal dichalcogenides. Phys. Rev. B 107, L201109 (2022).
Dong, J., Wang, J., Ledwith, P. J., Vishwanath, A. & Parker, D. E. Composite Fermi liquid at zero magnetic field in twisted MoTe2. Preprint at https://doi.org/10.48550/arXiv.2306.01719 (2023).
Wang, T., Devakul, T., Zalatel, M. P. & Fu, L. Topological magnets and magnons in twisted bilayer MoTe2 and WSe2. Preprint at https://doi.org/10.48550/arXiv.2306.02501 (2023).
Wei, H. P., Chang, A. M., Tsui, D. C. & Razeghi, M. Temperature dependence of the quantized Hall effect. Phys. Rev. B 32, 7016–7019 (1985).
Shahar, D., Tsui, D. C., Shayegan, M., Bhatt, R. N. & Cunningham, J. E. Universal conductivity at the quantum Hall liquid to insulator transition. Phys. Rev. Lett. 74, 4511–4514 (1995).
Chang, C.-Z. et al. Observation of the quantum anomalous Hall insulator to Anderson insulator quantum phase transition and its scaling behavior. Phys. Rev. Lett. 117, 126802 (2016).
Goldman, H., Reddy, A. P., Paul, N. & Fu, L. Zero-field composite Fermi liquid in twisted semiconductor bilayers. Preprint at https://arxiv.org/abs/2306.02513 (2023).
Winkler, R., Kotthaus, J. & Ploog, K. Landau band conductivity in a two-dimensional electron system modulated by an artificial one-dimensional superlattice potential. Phys. Rev. Lett. 62, 1177 (1989).
Ghiotto, A. et al. Quantum criticality in twisted transition metal dichalcogenides. Nature 597, 345–349 (2021).
Wang, L. et al. Correlated electronic phases in twisted bilayer transition metal dichalcogenides. Nat. Mater. 19, 861–866 (2020).
Kane, C. L. & Mele, E. J. Z2 Topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Acknowledgements
Measurements of the FQAH states are supported by DoE BES under award DE-SC0018171. Measurements of the integer QAH state are supported by the AFOSR FA9550-21-1-0177. Device fabrication and electrical transport measurements are partially supported by the Center on Programmable Quantum Materials, an Energy Frontier Research Center funded by DOE BES, under award DE-SC0019443. The understanding of magnetism and the topological phase diagram is partially supported by AFOSR Multidisciplinary University Research Initiative (MURI) programme, grant no. FA9550-19-1-0390. We also acknowledge the use of the facilities and instrumentation supported by the NSF MRSEC DMR-1719797. E.A. acknowledges support from the National Science Foundation Graduate Research Fellowship Program under grant no. DGE-2140004. W.Y. acknowledges support from the Research Grants Council of Hong Kong SAR (AoE/P-701/20, HKU SRFS2122-7S05) and the Croucher Foundation. C.-Z.C. also acknowledges the support from Gordon and the EPiQS Initiative of the Betty Moore Foundation (GBMF9063). K.W. and T.T. acknowledge support from the JSPS KAKENHI (grant nos 20H00354, 21H05233 and 23H02052) and the World Premier International Research Center Initiative (WPI), MEXT, Japan. This research acknowledges the use of the millikelvin optoelectronic quantum material laboratory supported by the M. J. Murdock Charitable Trust. J.-H.C. and X.X. acknowledge support from the Clean Energy Institute funded by the State of Washington.
Author information
Authors and Affiliations
Contributions
X.X. conceived and supervised the project. H.P., J.C. and E.A. fabricated and characterized the samples, assisted by Y.Z., J.Z., W.H., Z.L., C.H. and J.-H.C. H.P. and J.C. performed the transport measurements with inputs from C.Z.C. E.A. performed the magnetic circular dichroism measurements. J.C., D.C. and X.X. provided dilution fridge measurement support and designed the contact schemes. H.P., J.C., E.A., D.C., C.-Z.C., T.C., L.F., W.Y., D.X. and X.X. analysed and interpreted the results. X.L., C.W., T.C. and D.X. performed the Hartree–Fock calculations. T.T. and K.W. synthesized the hBN crystals. H.P., J.C., E.A., L.F., C.-Z.C., D.C., D.X. and X.X. wrote the paper with input from all authors. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
X.X., E.A., H.P. and J.C. have applied for a patent partially based on this work. The other authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Reproducibility of the quantum anomalous Hall effect.
a, Optical microscope images of three Hall bar devices studied in this work. Twist angles are indicated. Scale bar, 10 μm. b, Atomic force microscopy image of the device before contact gate fabrication. Scale bar, 2 μm. c, Contact geometry used in the main figures for the respective devices unless otherwise specified. The electrodes in dashed lines are floated. d, Magnetic field dependence of Rxx and Rxy at 100 mK. The quantization of Rxy and concomitant nearly vanishing Rxx demonstrates the robustness of the quantum anomalous Hall effect in tMoTe2 across a large range of twist angles.
Extended Data Fig. 2 Electric field dependence of v = −1 QAHE in device D(3.52°).
All data in the main panel are taken at 500 mK. a, Antisymmetrized |Rxy| (blue) and symmetrized Rxx (red) at |µoH| = 100 mT as a function of electric field (D/ε0) at v = −1. As D/ε0 is decreased below Dc/ε0 ≈ −50 mV/nm, Rxy quickly drops from the quantized value while Rxx increases rapidly to above 100 kΩ. This demonstrates an electric field induced transition from a QAH insulator to topologically trivial correlated insulator. Inset, symmetrized Rxx at |µoH| = 100 mT versus electric field D swept down and up near the phase transition. The absence of hysteresis implies a continuous topological phase transition. The data in the inset are taken at 1.6 K to minimize electrical noise from the contacts. b, Illustration of fitting used to extract the energy gap \(\Delta \) at selected electric field values. The Arrhenius equation and extracted \(\Delta \) are shown for D/ε0 = −70 and 0 mV/nm. At the critical field Dc/ε0 ≈ −50 mV/nm, the longitudinal resistance is nearly constant versus temperature. c, Energy gap as a function of electric field. Error bars are obtained from fitting variance. Grey dashed lines are guides to the eye. The closing and reopening of the gap versus D/ε0 are evidence for a continuous topological quantum phase transition between the QAH state and a topologically trivial correlated insulator. d, Antisymmetrized Rxy at magnetic field |µoH| = 100 mT as a function D/ε0 and carrier density (n) at 1.6 K. The filling factor (v) is shown on the top axis. Black regions denote areas with resistance too large to be reliably measured. The yellow dashed line bounds the region where Rxy is > 95 % of h/e2. e, Reflective magnetic circular dichroism (RMCD) signal versus D/ε0 and v at µoH = 100 mT and 1.6 K. The comparison with panel d shows that the critical electric field DFM/ε0 for suppressing the ferromagnetic state is larger than Dc/ε0 for the QAH insulator (the yellow dashed line is as in panel d). Therefore, the topologically trivial state is a ferromagnetic insulator. f, Hartree-Fock calculations of the out-of-plane spin (Sz) and energy gap normalized to the hopping t1 as a function of electric field. The system is in a topologically trivial ferromagnetic insulating state between Dc and DFM, and becomes non-valley polarized and hence non-ferromagnetic above DFM. The calculated Chern number is C = −1 (blue region) and 0 (grey region) for below and above Dc, respectively.
Extended Data Fig. 3 Electric field and temperature dependent QAH effect at v = −1.
Data are taken from device D(3.9°). a, ΔRxy versus magnetic field and electric field. Here, ΔRxy is obtained by taking the difference of Rxy between sweeping magnetic field up and down. ΔRxy starts to vanish around 150 mV/nm, signifying a topological phase transition. Large negative electric field values cannot be reached due to gate limits. b, Magnetic field dependence of Rxx and Rxy at selected temperatures. Rxy is nearly quantized even at 8 K. c, Rxx as a function of temperature at selected electric fields. Rxx is unsymmetrized and taken at 100 mT to avoid magnetic instability. d, Temperature dependent δRxy = |h/e2-Rxy| at selected electric fields, where Rxy is the antisymmetrized Hall resistance at ±100 mT. e, Colour plot of δRxy showing a phase transition near 150 mV/nm. f, Estimated thermal activation gap from the data in e. An energy gap of 35(2) K near zero electric field can be extracted, which is consistent with the value obtained from Rxx measurements, 32(2) K (see Fig. 2e).
Extended Data Fig. 4 Measurement configurations for Figs. 3 and 4, and characterization of electrical contacts for device D(3.7°).
We find that the contacts 7, 8, 11, and 12 isolate a single FQAH domain. a, Configuration for measuring Rxy. Current flows from contacts 8 to 12, and Hall voltage is measured between contacts 7 and 11. b, c, Reciprocal configurations for measuring Rxx. The symmetrized data (\({R}_{{\rm{xx}}}^{1}+{R}_{{\rm{xx}}}^{2}\))/2 from these configurations result in Rxx. The electrodes in dashed lines are floated. d, Configuration for two terminal measurements sourcing current from one contact while keeping all remaining contacts grounded (using contact 8 as a representative case). e, Doping dependence of contact conductance at 500 mK for the contacts used in the experiment. All contacts remain under 500 kΩ until resistance starts to increase near v = −1/2 as the system enters an insulating state.
Extended Data Fig. 5 Estimation of energy gap of the −2/3 FQAH state.
Data are taken from device D(3.7°) using the contact configuration in Extended Data Fig. 4. a, Arrhenius plot of Rxx. Solid line is the fit to equation \({R}_{0}{e}^{-\triangle /2{k}_{B}T}\). b, Arrhenius plot of δRxy = (3h/2e2-Rxy). Solid line is the fit to \({R}_{0}{e}^{-\triangle /{k}_{B}T}\). Extracted energy gaps from Rxx and Rxy measurements are similar, with values of 23(7)K and 21(4)K, respectively.
Extended Data Fig. 6 Temperature dependent measurements of the −3/5 state.
Data are taken from device D(3.7°). a, Magnetic field dependence of Rxx (top) and Rxy (bottom) at selected temperatures and D/ε0 = 0. Rxy is measured in the configuration described in Extended data Fig. 4a, while Rxx is obtained from the configurations in Extended Data Figs. 4b and c. b, Arrhenius plot of Rxx. Solid line is the fit to equation \({R}_{0}{e}^{-\triangle /2{k}_{B}T}\). c, Arrhenius plot of δRxy = (5h/3e2-Rxy). Solid line is the fit to \({R}_{0}{e}^{-\triangle /{k}_{B}T}\). Extracted energy gaps from Rxx and Rxy measurements are similar, with values of 15(3) K and 14(2) K, respectively. The nonvanishing Rxx at base temperature can arise from large contact resistance, twist angle disorder, or interlayer electric polarization domains that connect probing contacts.
Extended Data Fig. 7 Anomalous Hall state at half-filling in an additional device D(3.9°).
a, Rxx and Rxy versus magnetic field near v = −1/2, D/ε0 = 0, and at a temperature of 100 mK. b, Magnetic field dependent Rxx (top) and Rxy (bottom) at selected temperatures. c, ΔRxy versus magnetic field and temperature. Here, ΔRxy is the difference between Rxy for magnetic field swept up and down. d, Temperature dependent symmetrized Rxx and antisymmetrized Rxy at ±5 mT and v near −1/2. A phase transition between 2–4 K is evident.
Extended Data Fig. 8 Temperature dependent transport for −1/2 anomalous Hall state from D(3.7°).
Data are taken from device D(3.7°) using the contact configuration in Extended Data Fig. 4. a, Magnetic field dependent Rxx and Rxy at different temperatures near v = −1/2 and D/ε0 = 0. b, ΔRxy versus magnetic field and temperature. Here, ΔRxy is the difference between Rxy for magnetic field swept up and down.
Source data
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Park, H., Cai, J., Anderson, E. et al. Observation of fractionally quantized anomalous Hall effect. Nature 622, 74–79 (2023). https://doi.org/10.1038/s41586-023-06536-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-023-06536-0
This article is cited by
-
Flat bands, strange metals and the Kondo effect
Nature Reviews Materials (2024)
-
Weird new electron behaviour in stacked graphene thrills physicists
Nature (2024)
-
Uncovering the spin ordering in magic-angle graphene via edge state equilibration
Nature Communications (2024)
-
Evidence of the fractional quantum spin Hall effect in moiré MoTe2
Nature (2024)
-
Manipulation of chiral interface states in a moiré quantum anomalous Hall insulator
Nature Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.