Introduction

In the past few decades, quantum bits implemented as superconducting circuits have become promising candidates for building blocks of large-scale quantum computers1,2,3,4. To increase the scalability of these architectures, robust methods of generating single photons for quantum computation in the propagating modes and for transferring information between multiple superconducting qubits over relatively long distances are of recent interest. In the optical domain, different photonic qubit encodings have been demonstrated before for such purposes5. However, optical single-photon generation protocols are often probabilistic rather than deterministic, limiting success probability6. Moreover, conversion of quantum information stored in superconducting qubits operated in the microwave regime to optical photons suffers from low efficiency and limited bandwidth7,8. Schemes focused on generating photons at microwave frequencies and their characterization are therefore of great interest.

Photonic qubit encoding can be realized by constructing a set of computational basis states with one or more orthogonal modes of light. In the microwave regime, single-rail (single-mode) encoding has been demonstrated by using the photon number states of a propagating microwave qubit to transfer information between two superconducting qubits over a transmission line with fidelity close to 0.89,10,11,12. However, photon loss reduces the transfer fidelity greatly, as decayed photon states cannot be distinguished readily. In addition, the phase information in a single-rail photonic qubit state is stored as the relative phase between the propagating qubit mode and a separate phase reference. Thus, the reference must be shared between any hardware operating the nodes of a quantum network that the photonic qubit will interact with, reducing the practicality of single-rail encoding in large networks.

As an alternative to the single-rail encoding, dual-rail (dual-mode) encoding has been demonstrated in the optical regime in the form of polarization13,14,15 and time-bin qubits16,17. Occupation of a single photon in one of two orthogonal temporal modes functions as the basis of the time-bin qubit. Time-bin encoding allows one to readily determine loss of information during transfer with a photon number parity measurement5,18, and the qubit state is more robust against dephasing, as the phase information is stored in the relative phase between the two temporal modes. Thus, time-bin qubits do not require sharing of a phase reference19. Owing to these favorable properties, a linear optical scheme for quantum computation with time-bin qubits has been proposed5. However, only the loss-robustness of the microwave time-bin qubit has been demonstrated. The demonstration was based on discrete-variable measurements of superconducting qubits as a part of a transfer protocol, thus being limited to a single qubit of information20. A different approach is necessary for full state tomography of a general two temporal mode state or cluster states with multiple modes and qubits of information. Ideally, for a scalable characterization method, only a single detector should be necessary regardless of the number of modes.

In this work, we experimentally demonstrate on-demand generation of microwave time-bin qubits with a superconducting transmon qubit21 and show how the time-bin qubit retains phase information and can be loss-corrected. Our scheme allows us to generate and shape the single-photon wave packet as well as to generate any superposition state of the time-bin qubit with variable spacing between the temporal modes. We perform Wigner tomography of microwave signal in two temporal modes by measuring the quadrature distributions with a flux-driven Josephson parametric amplifier22 and a single heterodyne detector23. With the Josephson parametric amplifier (JPA), we can rapidly change the measurement quadrature for each temporal mode independently in a single shot. We reconstruct the quantum state of the signal with a maximum-likelihood method23,24. We compare the state preparation fidelity of the dual-rail time-bin qubit with a single-rail number-basis qubit and a transmon qubit. We demonstrate that correcting photon loss of the time-bin qubit state improves the fidelity significantly. By removing the phase-locking between the single-photon source and the detector, we observe that the single-rail photonic qubit state dephases completely owing to the lack of a stable phase reference, whereas the time-bin qubit state is unaffected. This demonstrates that the phase information of the dual-rail qubit is contained in the relative phase between the two modes and that using the time-bin qubit in a quantum network does not require a shared phase reference.

Results

System

To generate a single photon, we consider a coherently driven circuit quantum electrodynamical setup where a superconducting transmon qubit is dispersively coupled to a 3D microwave cavity with a resonance frequency ωc∕2π = 10.619 GHz. The dynamics of the system are described in the rotating frame of the drive by the Hamiltonian

$$\begin{array}{ll}{\mathcal{H}}/\hslash =({\omega }_{{\rm{c}}}-{\omega }_{{\rm{d}}}){a}^{\dagger }a+({\omega }_{{\rm{ge}}}-{\omega }_{{\rm{d}}}){b}^{\dagger }b+\frac{\alpha }{2}{b}^{\dagger }{b}^{\dagger }bb\\ \,+\,g({a}^{\dagger }b+a{b}^{\dagger })+\frac{1}{2}\left[\Omega (t){a}^{\dagger }+{\Omega }^{* }(t)a\right].\end{array}$$
(1)

The qubit is coupled to the cavity with coupling strength g∕2π = 156.1 MHz and it is driven by coherent microwaves at frequency ωd with time-dependent complex amplitude Ω(t) through the cavity. In Eq. (1), a and b are defined as the cavity and transmon annihilation operators, and ωge∕2π = 7.813 GHz is the qubit \(\left|{\rm{g}}\right\rangle\)−\(\left|{\rm{e}}\right\rangle\) transition frequency separated from the \(\left|{\rm{e}}\right\rangle\)−\(\left|{\rm{f}}\right\rangle\) transition frequency ωef = ωge + α by the transmon anharmonicity α∕2π = −340 MHz. The cavity and qubit are dispersively coupled, i.e., \(\left|{\omega }_{{\rm{ge}}}-{\omega }_{{\rm{c}}}\right|\gg g\), which allows us to readout the qubit state based on the qubit state-dependent dispersive shift of the cavity resonance frequency. The cavity is coupled to an external transmission line with an external coupling rate κex∕2π = 2.91 MHz. The relaxation and coherence times between the \(\left|{\rm{g}}\right\rangle\)–\(\left|{\rm{e}}\right\rangle\) and \(\left|{\rm{e}}\right\rangle\)–\(\left|{\rm{f}}\right\rangle\) states are \({T}_{1}^{{\rm{ge}}}=\) 26 μs, \({T}_{1}^{{\rm{ef}}}=\) 15 μs, and \({T}_{2}^{{\rm{ge}}}=\) 15 μs, \({T}_{2}^{{\rm{ef}}}=\) 16 μs, respectively.

Dynamics of time-bin qubit generation

The state of two time-bin modes can be represented in the photon number basis in two orthogonal temporal modes

$$\left|{\psi }_{{\rm{TL}}}\right\rangle =\mathop{\displaystyle\sum }\limits_{n,m = 0}^{\infty }{C}_{nm}\left|nm\right\rangle ,$$
(2)

where \(\left|nm\right\rangle := {\left|n\right\rangle }_{{\rm{E}}}\otimes {\left|m\right\rangle }_{{\rm{L}}}\) represents the photon number states of the earlier (E) and later (L) modes, respectively, with \(\mathop{\sum }\nolimits_{n,m = 0}^{\infty }| {C}_{nm}{| }^{2}=1\).

The protocol for quantum state transfer from a superconducting qubit to a time-bin qubit is shown in Fig. 1a. We prepare the superconducting qubit in a superposition state \({\alpha }_{{\rm{q}}}\left|{\rm{g}}\right\rangle +{\beta }_{{\rm{q}}}\left|{\rm{e}}\right\rangle\) and transfer the state to \({\alpha }_{{\rm{q}}}\left|{\rm{e}}\right\rangle +{\beta }_{{\rm{q}}}\left|{\rm{f}}\right\rangle\) with a sequence of πef and πge pulses at frequencies ωef and ωge, respectively.

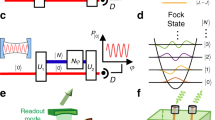
Fig. 1: Dynamics of time-bin qubit generation and measurement setup.
figure 1

a Driven interaction between a superconducting qubit and 3D cavity for the generation of a microwave time-bin qubit propagating along a transmission line. The two energy diagrams for the qubit–cavity system describe the generation protocol. b Simplified configuration for generating and measuring a time-bin qubit at frequency \({\omega }_{{\rm{c}}}^{{\rm{g}}}\) with Josephson parametric amplifier (JPA) realized heterodyne measurement. Three different microwave sources are used in the experiment to generate signal at the qubit control frequencies ωge and ωef, \(\left|{\rm{f}}0\right\rangle\)−\(\left|{\rm{g}}1\right\rangle\) transition frequency ωf0g1, dispersive cavity readout frequency ωRO, JPA pump frequency ωp, and demodulation local oscillator frequency \({\omega }_{{\rm{c}}}^{{\rm{LO}}}\). c Measured marginal distribution of a single-rail single-photon qubit state (red histogram) as a function of a given quadrature of the generated signal. The dark blue dashed line represents a theoretical fit to the data with 95% confidence intervals (light blue zone). d Reconstructed Wigner function of the signal with quadratures q and p defined corresponding to [q, p] = i. The data in the figures has not been corrected for detection inefficiency.

Full size image

We induce the transition between the \(\left|{\rm{f}}0\right\rangle\) and \(\left|{\rm{g}}1\right\rangle\) states of the combined qubit–cavity system with a drive pulse to generate a shaped single photon inside a transmission line25. The \(\left|{\rm{f}}0\right\rangle\)–\(\left|{\rm{g}}1\right\rangle\) transition frequency is defined as ωf0g1 = 2ωge + α − ωc. When the drive frequency matches this transition, the microwave-induced effective coupling between \(\left|{\rm{f}}0\right\rangle\) and \(\left|{\rm{g}}1\right\rangle\) can be derived from the system Hamiltonian in Eq. (1)

$${g}_{{\rm{eff}}}(t)=\frac{\sqrt{2}\alpha {g}^{2}}{4{({\omega }_{{\rm{c}}}-{\omega }_{{\rm{ge}}})}^{3}}\Omega (t).$$
(3)

Here, the complex amplitude \(\Omega (t)=\exp [i\phi (t)]| \Omega (t)|\) has a phase degree of freedom ϕ(t). By applying this coupling pulse to the sample we can generate a photon inside the cavity. The photon in the cavity will decay to the waveguide at the external coupling rate κex. Thus, the coefficient βq is transferred to the photon in the E mode of the time-bin qubit. The second coefficient, αq, is transferred to the propagating microwave mode by driving the qubit with a πef pulse and the coupling pulse once afterwards.

If the generation protocol has ideal efficiency, the coefficients αq and βq are transferred to the modes \(\left|01\right\rangle\) and \(\left|10\right\rangle\) as C01 = αq and C10 = βq. As the original qubit state is normalized, \({\left|{C}_{{\rm{01}}}\right|}^{2}+{\left|{C}_{{\rm{10}}}\right|}^{2}=1\), and all of the other coefficients in Eq. (2) become zero. Thus, the transfer process of the qubit state to propagating microwave mode in the temporal mode basis represents the mapping \({\alpha }_{{\rm{q}}}\left|{\rm{g}}\right\rangle +{\beta }_{{\rm{q}}}\left|{\rm{e}}\right\rangle \mapsto {\alpha }_{{\rm{q}}}\left|01\right\rangle +{\beta }_{{\rm{q}}}\left|10\right\rangle\). We can therefore define the temporal modes \(\left|01\right\rangle \equiv \left|{\rm{L}}\right\rangle\) and \(\left|10\right\rangle \equiv \left|{\rm{E}}\right\rangle\) as the basis states of a dual-rail time-bin qubit. One should note that the time-bin qubit basis states have a single photon, meaning that a valid qubit state can be confirmed with a parity measurement of the total photon number in the two temporal modes.

Characterization of the experimental setup

A schematic of the experimental configuration for generating and measuring the propagating time-bin qubit state is shown in Fig. 1b. We input the qubit control pulses, qubit state readout pulse, and coupling pulse, to the cavity cooled down to 30 mK inside a dilution refrigerator. We amplify the generated time-bin qubit signal with a flux-driven JPA operated in the degenerate mode by driving the JPA with two successive microwave pulses at frequency \({\omega }_{{\rm{p}}}=2{\omega }_{{\rm{c}}}^{{\rm{g}}}\) where \({\omega }_{{\rm{c}}}^{{\rm{g}}}/2\pi =\) 10.628 GHz is the dressed cavity frequency when the qubit is in the ground state. The measured signal is demodulated with a local oscillator at frequency \({\omega }_{{\rm{c}}}^{{\rm{LO}}}\) shifted from \({\omega }_{{\rm{c}}}^{{\rm{g}}}\) by the sideband frequency −2π × 50 MHz.

We estimate the measurement efficiency for our generation and characterization system by measuring the marginal distribution along a given quadrature in phase space and reconstructing the Wigner function of a single-rail single-photon state \(\left|1\right\rangle\) in Fig. 1c, d. We only consider measurements where the qubit is in the ground state both before and after the measurement. In the marginal distribution of the measured signal, we extract from a theoretical fit26 a single-photon probability of \({P}_{\left|1\right\rangle }=\mathrm{0.591 \pm 0.038}\) with 95% confidence intervals. We obtain a fidelity of 0.556 ± 0.009 for the reconstructed Wigner function and observe a negative region in the quasiprobability distribution near the origin of the phase space (Fig. 1d), demonstrating negativity of the measured state without loss correction for detection inefficiency. We define the error interval of the fidelity as three times the standard deviation obtained from bootstrapping27 of the tomography data. We obtain from an analytical calculation (see Section 2 of Supplementary Methods) the possible maximum generation efficiency of ηgen = 0.83 ± 0.02 with the parameters in our system, resulting in the minimum measurement efficiency of ηmeas = 0.67 ± 0.01, comparable to recent experiments in similar systems28,29,30 and mostly explained by the insertion loss of the circulators and isolators.

Quadrature distribution of microwave time-bin qubit signal

The pulse sequence used in the experiment for time-bin qubit generation is shown as a quantum circuit in Fig. 2a and as temporal waveforms with different angular frequencies in Fig. 2b. We perform a z-basis dispersive readout on the qubit state28,31 with an assignment fidelity of 0.99 to initialize the qubit, and at the end of the generation sequence to measure whether the transfer sequence results in the qubit being in the ground state or not.

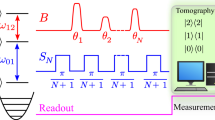
Fig. 2: Time-bin qubit generation and characterization sequence.
figure 2

a Quantum circuit representation of time-bin qubit generation. (i) Preparation of an arbitrary transmon qubit state. (ii) Transfer of the transmon qubit state to the first temporal mode of a time-bin qubit and measurement of the first quadrature. (iii) Transfer of the remaining transmon qubit population to the second temporal mode and measurement of the second quadrature. (iv) The process ends with a measurement of the qubit state. b Corresponding time-domain pulse sequence. The pulses are generated at five different frequencies depicted in Fig. 1. The JPA pump pulses have phases φE and φL. c Measured (orange line) and numerically simulated (black dashed line) mean field amplitude squared of the generated time-bin qubit. d Measured distribution of quadratures (qφE, qφL) for the two temporal modes of a time-bin qubit prepared in state \((1/\sqrt{2})(\left|{\rm{L}}\right\rangle +\left|{\rm{E}}\right\rangle )\). Each of the three distributions correspond to 72637 post-selected samples measured for quadratures with phase difference ΔφEL = φE − φL conditioned on the transmon qubit being in the ground state both before and after the time-bin generation.

Full size image

In Fig. 2c, we show the measured and simulated mean field amplitude squared ∣〈aout(t)〉∣2 of the state \((1/\sqrt{2})\left|00\right\rangle +(1/2)\left|10\right\rangle +(1/2)\left|01\right\rangle\) as a function of time. The magnitude is calculated according to the theory in Section 2 of the Supplementary Methods. The measured amplitude is normalized to match the simulated amplitude by defining that the integrals calculated over the time interval for the squared amplitudes must be equal. We only consider here measurement events where the transmon qubit was measured as being in the ground state both before and after the generation sequence. We utilize the shape of the measured temporal mode amplitudes to calculate the quadrature distributions of the time-bin qubit. The correlation between the measurements changes based on the selected quadratures, as shown in Fig. 2d.

Characterization of microwave photonic qubit states

We experimentally prepare the transmon, single-rail number basis and time-bin qubits in the six cardinal states of the Bloch sphere, as shown in Fig. 3a. We define the number-basis qubit state basis as \(\left|0\right\rangle \equiv {\left|0\right\rangle }_{{\rm{S}}}\) and \(\left|1\right\rangle \equiv {\left|1\right\rangle }_{{\rm{S}}}\), corresponding to no excitation or a single excitation in a single mode. The number-basis qubit states are generated with a sequence similar to the time-bin generation sequence in Fig. 2, but with only the first two qubit control pulses and the first coupling and JPA pump pulses. A series of qubit state readouts along the three Bloch sphere axes are performed to reconstruct the transmon qubit state. All of the measurements are performed in single-shot.

Fig. 3: Reconstructed qubit states.
figure 3

a Reconstructed six cardinal states and their state preparation fidelities measured for a transmon qubit (T) (basis: \(\left|{\rm{g}}\right\rangle\) and \(\left|{\rm{e}}\right\rangle\)), a photonic number-basis qubit (S) (basis: \({\left|0\right\rangle }_{{\rm{S}}}\) and \({\left|1\right\rangle }_{{\rm{S}}}\)), and a time-bin qubit (TB) (basis: \(\left|{\rm{L}}\right\rangle\) and \(\left|{\rm{E}}\right\rangle\)). The states \(\left|0\right\rangle\) and \(\left|1\right\rangle\) correspond to the basis states of each qubit in the respective order. The time-bin qubit fidelity is shown both without and with photon loss correction (LC). The measured transmon qubit, number-basis qubit, and loss-corrected time-bin qubit states are shown inside the Bloch sphere. b Average fidelity calculated over all of the six states for each qubit. The error estimates correspond to three times the standard deviation (99.7% confidence interval) obtained from bootstrapping of the tomography data.

Full size image

We calculate the fidelity of each prepared state as

$${\mathcal{F}}=\left\langle {\psi }_{{\rm{t}}}\right|\rho \left|{\psi }_{{\rm{t}}}\right\rangle ,$$
(4)

where the pure target state is defined as \(\left|{\psi }_{{\rm{t}}}\right\rangle\) and ρ is the measured qubit state.

Transmon qubit tomography

For the transmon qubit states, we only consider measurement events where the qubit is initially measured to be in the ground state. On average, 87.5% of our measurement events fulfill this condition. The relatively high initial excited state population may be explained by noise from the qubit control line32. The population can be reduced with cooling techniques33,34. Given the above condition, we measure a state preparation fidelity of \({{\mathcal{F}}}_{{\rm{T}}}^{{\rm{avg}}}=\mathrm{0.987 \pm 0.001}\) averaged over the six cardinal states (Fig. 3b), limited mainly by the qubit control pulse fidelity and readout assignment fidelity.

Single-rail number-basis qubit tomography

For the single-rail states, we post-select the measurement events where both of the readouts before and after the generation sequence result in the qubit state being assigned to the ground state. On average, we keep 82.6% of all data in the tomography process.

We prepare the single-rail number-basis qubit states with a fidelity of \({{\mathcal{F}}}_{{\rm{SR}}}^{{\rm{avg}}}=\mathrm{0.781 \pm 0.003}\), noticeably lower than the transmon qubit states. The difference in fidelity is caused by relaxation and dephasing of the transmon qubit state during single-photon generation and photon loss during photon transfer from the qubit to the JPA and heterodyne detector. The effect of photon loss can be observed in the Bloch sphere as a bias towards the \(\left|0\right\rangle\) state for all of the six cardinal states.

Time-bin qubit tomography

We post-select the time-bin measurement events where both of the readouts result in the transmon qubit being in the ground state corresponding to 80.4% of all measurements. We discuss the other measurement events in more detail in Section 7 of the Supplementary Methods.

Without loss correction, we measure an average state preparation fidelity of \({{\mathcal{F}}}_{{\rm{TB}}}^{{\rm{avg}}}=\mathrm{0.434 \pm 0.001}\). As the generation sequence is longer than that of the single-rail qubit, the effect of qubit control pulse infidelity and qubit dephasing and relaxation on the state preparation fidelity also becomes stronger. Furthermore, we emulate an effective photon number parity measurement on the time-bin qubit density matrices by projecting the full two-mode density matrix to the time-bin qubit subspace spanned by \(\left|{\rm{E}}\right\rangle\) and \(\left|{\rm{L}}\right\rangle\), as detailed in Section 6 of the Supplementary Methods. After the effective parity measurement, we obtain a loss-corrected time-bin qubit average state fidelity of \({{\mathcal{F}}}_{{\rm{TB,LC}}}^{{\rm{avg}}}=\mathrm{0.910 \pm 0.002}\).

Phase robustness of the time-bin qubit

We measure and reconstruct the density matrices of the single-rail qubit and time-bin qubits for the coherent superposition states \((1/\sqrt{2})({\left|0\right\rangle }_{{\rm{S}}}+{\left|1\right\rangle }_{{\rm{S}}})\) and \((1/\sqrt{2})(\left|{\rm{L}}\right\rangle +\left|{\rm{E}}\right\rangle )\) when the photon source does and does not share the same relative phase reference with the detector, as shown in Fig. 4a, b, respectively. To experimentally realize this condition, we use a separate reference clock for the microwave source, which generates the coupling pulse carrier signal than for the other two microwave sources used for qubit control, JPA operation, and demodulation of single-photon signal. We also perform photon loss correction on the time-bin qubit density matrices.

Fig. 4: Effect of the lack of a shared phase reference on photonic qubit generation.
figure 4

Measured real parts of density matrix elements for a single-rail number-basis qubit (basis: \({\left|0\right\rangle }_{{\rm{S}}}\) and \({\left|1\right\rangle }_{{\rm{S}}}\)) and a loss-corrected time-bin qubit (basis: \(\left|{\rm{L}}\right\rangle\) and \(\left|{\rm{E}}\right\rangle\)). a All of the microwave sources used share the same reference clock (phase reference). b There is no shared reference clock. The Bloch spheres refer to the stability of the phase between each measured state. In the bar plots, the rectangles indicate the ideal values and the error bars describe three times the standard deviation obtained from bootstrapping.

Full size image

When all of the microwave sources share the same external rubidium clock (Fig. 4a), phase coherence is maintained between the generated photons, and the tomography results in a single-rail qubit state fidelity of \({{\mathcal{F}}}_{{\rm{SR}},X}^{{\rm{shared}}}=\mathrm{0.811 \pm 0.007}\) and time-bin qubit state fidelity of \({{\mathcal{F}}}_{{\rm{TB}},X}^{{\rm{shared}}}=\mathrm{0.901 \pm 0.006}\). The time-bin qubit is slightly more coherent than the single-rail qubit, because of a slow phase reference drift, which occurs even with a shared external clock and perhaps also in-part owing to the photon loss correction. In Fig. 4b, we disconnect the microwave source for the coupling pulse from the shared clock. Owing to the phase drift between the two clocks, the single-photon signal generated by the coupling pulse has a different phase reference each time. Thus, as we observe in the measured off-diagonal matrix elements, the measured single-rail qubit is dephased completely, resulting in a single-rail preparation fidelity of \({{\mathcal{F}}}_{{\rm{SR}},X}^{{\rm{sep}}}=\mathrm{0.500 \pm 0.008}\). In contrast, for the time-bin qubit, the phase information is not lost since the relative phase between the two temporal modes determines the phase information of the qubit, resulting in a time-bin qubit state fidelity of \({{\mathcal{F}}}_{{\rm{TB}},X}^{{\rm{sep}}}=\mathrm{0.899 \pm 0.006}\).

Discussion

We successfully performed on-demand generation of microwave time-bin qubits by driving a 3D circuit-QED system in dispersive regime and characterized the resulting quantum states with maximum-likelihood estimation of two-mode signal amplified by a JPA in heterodyne measurement. Our tomography method allowed us to perform Wigner tomography of a general two temporal mode microwave state with a single detector by switching the measurement quadrature in time between the temporal modes. We measured an average time-bin qubit state preparation fidelity of 0.910 after loss correction. We also demonstrated that the phase information of the time-bin qubit is stored in the relative phase of the temporal modes and that the lack of a shared phase reference does not cause the time-bin qubit to dephase. By performing a quantum non-demolition measurement of the photon number parity in the time-bin qubit with the method in refs 23,29,35, it is possible to perform loss-detection on the time-bin qubits to increase the fidelity of information transfer and distributed computation in a superconducting qubit network by an amount corresponding to the photon loss. Our tomography method can also be extended to microwave cluster states with an arbitrary number of temporal modes without any additional detector hardware by adding a new JPA pump pulse for each additional temporal mode. The quadrature detection can be used to realize remote state preparation schemes36,37. It is also possible to combine our method with an entanglement witness38 or select the measurement quadratures adaptively to characterize the entanglement and state with minimal number of measurements.

Methods

Pulse calibration

We define the qubit control pulses as Gaussian-shaped pulses while the shape of the coupling pulse is defined as a cosine pulse \([1-\cos (2\pi t/w)]/2\) with width w for t ∈ [0, w]. We optimize the width, separation, amplitude, phase, and frequency of all pulses in parameter sweep experiments by maximizing the assignment and state preparation fidelities for each parameter separately. The experimental setup used for pulse generation is detailed in Section 1 of the Supplementary Methods. In addition, we apply DRAG39 to the qubit control pulses and chirp the coupling pulses to limit the effect of the \(\left|{\rm{f}}\right\rangle\)-state Stark shift affecting the phase of the generated photon wave packet9. We also add a constant phase shift to the second coupling pulse relative to the first to reduce the effect of \(\left|{\rm{e}}\right\rangle\)-state Stark shift. The optimization of the coefficients for DRAG and chirping is detailed in Sections 3, 4, and 6 of the Supplementary Methods.

Wigner tomography of two temporal modes

We use JPA phase-sensitive amplification together with heterodyne measurement to reconstruct the full quantum state of the single-rail number basis and time-bin qubits with iterative maximum-likelihood estimation performed on measured quadrature distributions of the temporal modes based on refs 24,40.

To change the quadrature of amplification independently for two temporal modes, we select pairs of JPA pump pulse phases (φE, φL) ∈ [0, 2π] × [0, 2π] corresponding to amplification of each temporal mode. For a single phase pair, we obtain measured quadrature values (qE, qL). A measured two-mode state ρEL matches a given set of the four values above with a probability amplitude \({\rm{Tr}}[{\rho }_{{\rm{EL}}}\Pi ({\varphi }_{{\rm{E}}},{q}_{{\rm{E}}},{\varphi }_{{\rm{L}}},{q}_{{\rm{L}}})]\). Here, we have defined the projection operator

$$\Pi ({\varphi }_{{\rm{E}}},{q}_{{\rm{E}}},{\varphi}_{{\rm{L}}},{q}_{{\rm{L}}}) =\left|{\varphi}_{{\rm{E}}},{q}_{{\rm{E}}},{\varphi}_{{\rm{L}}},{q}_{{\rm{L}}}\right\rangle \left\langle {\varphi}_{{\rm{E}}},{q}_{{\rm{E}}},{\varphi}_{{\rm{L}}},{q}_{{\rm{L}}}\right|.$$
(5)

In order to find the optimal density matrix ρopt that matches the measured probabilities of all outcomes \(\left({\varphi }_{{\rm{E}},{\rm{j}}},{q}_{{\rm{E}},{\rm{j}}},{\varphi }_{{\rm{L}},{\rm{j}}},{q}_{{\rm{L}},{\rm{j}}}\right)\) in our experiment, we iteratively search for the density matrix that maximizes the logarithm of the likelihood function

$$\mathrm{ln}\,[L(\rho )]=\mathop{\displaystyle\sum }\limits_{j}\mathrm{ln}\,\left\{{\rm{Tr}}\left[\rho \Pi \left({\varphi }_{{\rm{E}},j},{q}_{{\rm{E}},j},{\varphi }_{{\rm{L}},j},{q}_{{\rm{L}},j}\right)\right]\right\},$$
(6)

where we have assumed that the set \(\left({\varphi }_{{\rm{E}},{\rm{j}}},{q}_{{\rm{E}},{\rm{j}}},{\varphi }_{{\rm{L}},{\rm{j}}},{q}_{{\rm{L}},{\rm{j}}}\right)\) forms a dense parameter space. We perform the maximization by defining an iterative operator

$$R(\rho )=\mathop{\displaystyle\sum }_{j}\frac{\Pi ({\varphi }_{{\rm{E}},{\rm{j}}},{q}_{{\rm{E}},{\rm{j}}},{\varphi }_{{\rm{L}},{\rm{j}}},{q}_{{\rm{L}},{\rm{j}}})}{{\rm{Tr}}[\rho \Pi ({\varphi }_{{\rm{E}},{\rm{j}}},{q}_{{\rm{E}},{\rm{j}}},{\varphi }_{{\rm{L}},{\rm{j}}},{q}_{{\rm{L}},{\rm{j}}})]},$$
(7)

which has a property R(ρopt)ρoptR(ρopt) ∝ ρopt. This property allows us to iteratively calculate ρopt by \({\rho }_{k+1}=R({\rho }_{k}){\rho }_{k}R({\rho }_{k})/{\rm{Tr}}[R({\rho }_{k}){\rho }_{k}R({\rho }_{k})]\). We start the iteration from an initial state \({\rho }_{0}=I/{\rm{Tr}}(I)\) and calculate the logarithm of the likelihood for each density matrix in the iteration until convergence.

We perform the above iteration numerically and solve the reconstructed density matrix in the Fock basis of two temporal modes by calculating the two-mode matrix elements \(\left\langle {n}_{{\rm{E}}},{n}_{{\rm{L}}}\right|R(\rho )\left|{m}_{{\rm{E}}},{m}_{{\rm{L}}}\right\rangle\) of the iterative operator for photon numbers nE, nL, mE, and mL in the two modes.

We measured a JPA gain of 26.8 dB for the single-photon signal (See Section 5 of the Supplementary Methods). To reduce the amount of measurements, we perform the tomography for 12 × 12 different quadratures in the two modes. For each quadrature pair, we measure 104 samples. We truncate the two-mode density matrix in the tomography by limiting the maximum amount of photons in a single temporal mode to two.

Bootstrapping of the reconstructed density matrices

We estimate the error of the reconstructed density matrices and state preparation fidelity of the qubit states by bootstrapping the tomography measurement events27. We resample the data measured for each qubit state and perform maximum-likelihood estimation on the resampled data set to obtain a bootstrapped density matrix. By performing this procedure for a number of bootstrapping samples, we can calculate the distribution and standard deviation of the reconstructed density matrix elements. We use 250 bootstrapping samples for each tomography measurement.