Characterization and control of open quantum systems beyond quantum noise spectroscopy

Abstract

The ability to use quantum technology to achieve useful tasks, be they scientific or industry related, boils down to precise quantum control. In general it is difficult to assess a proposed solution due to the difficulties in characterizing the quantum system or device. These arise because of the impossibility to characterize certain components in situ, and are exacerbated by noise induced by the environment and active controls. Here, we present a general purpose characterization and control solution making use of a deep learning framework composed of quantum features. We provide the framework, sample datasets, trained models, and their performance metrics. In addition, we demonstrate how the trained model can be used to extract conventional indicators, such as noise power spectra.

Introduction

Accurately controlling the dynamics of open quantum systems is a central task in the successful implementation of quantum-enhanced technologies. Doing so to the highest possible level of accuracy involves a two-stage approach: first, quantum noise spectroscopy (QNS)^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21} protocols are used to infer characteristics of the open quantum system that affect the open quantum system dynamics, and then optimal control routines (OC) exploit this information to minimize the effect of noise and produce high-quality gates^22,23.

In this work, we go beyond the aforementioned approach and pose the problem in a machine-learning (ML) context. By doing so, we provide a common language in which the “learning” (equivalent to QNS) and “validation” (the precursor to OC) cycles are directly related to the objective of controlling an open quantum system. Notably, we show that doing so considerably extends the real-world applicability of the aforementioned two-stage strategy, as one can forgo some of the non-trivial control and model assumptions necessary for the implementation of sufficiently general QNS protocols. The success of the approach relies on the fact that the ML algorithm learns about the dynamics relative to a given set of control capabilities, which effectively reduces the complexity of the problem in a way meaningful to experimental constraints (see also²⁴ for a formal analysis of this problem).

The guiding principles of this work were to develop a framework that enables us to have models that are independent on any assumptions. It has to be suitable for estimating physically relevant quantities. Moreover finally, it should have the capacity to do standard tasks such as decoherence suppression and quantum control.

The proposed method is based on a graybox approach, where all the known relations from quantum mechanics are implemented as custom whitebox layers—quantum features—while the parts that depend on assumptions on noise and control are modeled by standard blackbox machine-learning layers. In this paper, we show how to construct such a model. The proposed model can be trained from experimental data consisting of sets of control pulses, and corresponding quantum observables. However, in this paper, we do not have access to an actual experiment, and thus we train the algorithm and asses its performance using synthesized datasets, obtained by computer simulations of a noisy qubit system. The results show high accuracy in terms of prediction error. We also show the possibility of utilizing the trained model to do basic quantum control operations. This paper opens the door for a number of possible novel machine-learning methods in the fields of quantum dynamics and control.

This work complements the existing literature applying classical machine-learning to the quantum domain. Recently, machine-learning and its deep learning framework²⁵ have been applied to many areas of quantum information, and physics more generally. Application areas include quantum control^26,27,28, characterization of quantum systems^29,30,31,32, experiment design^33,34,35, quantum cryptography³⁶, and quantum error correction^37,38,39. A related approach is Bayesian learning that was applied for Hamiltonian learning^40,41, quantum noise spectroscopy⁴², and characterization of devices⁴³.

In broad terms, our objective is to effectively characterize and accurately predict the dynamics of a two-level open quantum system, i.e., a qubit interacting with its environment, undergoing user-defined control picked from a fixed set, e.g., consistent with the control capabilities available to a given experimental platform. In what follows we make this statement precise.

For concreteness we start by choosing a model for our dynamics. We will consider a qubit evolving in the presence of both quantum and classical noise¹⁰ via a time-dependent Hamiltonian of the form,

$$H(t)=\mathop {\sum}\limits_{\alpha = x,y,z}{\sigma }_{\alpha }\otimes {B}_{\alpha }(t)+{H}_{\text{ctrl}}(t),$$

(1)

where ${B}_{\alpha }(t)={\tilde{B}}_{\alpha }(t)+{\beta }_{a}(t){I}_{B}$ is an operator capturing the effect of a quantum bath, via the operator ${\tilde{B}}_{\alpha }(t)$ typically resulting by working in the interaction picture with respect to the bath internal Hamiltonian, and classical noise, via the stochastic process β_a(t). Control is implemented via the Hamiltonian

$${H}_{\text{ctrl}}(t)=\Omega \frac{{\sigma }_{z}}{2}+\mathop {\sum}\limits_{\alpha = \{x,y,z\}}{f}_{\alpha }(t)\frac{{\sigma }_{\alpha }}{2},$$

(2)

where Ω denotes the energy gap of the qubit, f_α(t) implements the user-defined control pulses along the α-direction, and σ_α is the α Pauli matrix. Notice that this generic model can accommodate classical noise process simply by making B_α(t) = β_α(t)I_B, with β_α(t) an stochastic process. In all equations and simulations in this paper, we work with units, where $\hbar$ = 1. Since we are interested in predicting the dynamics of the qubit in a time interval [0, T], we will be interested in the expectation value ${\mathbb{E}}{\{O(T)\}}_{\rho }$ of observables O at time T given an arbitrary initial state of the system ρ and a choice of {f_α(t)}.

While these expectation values contain the necessary information, it will be convenient to further isolate the effect of the noise. To this end we proceed as follows. Our starting point is the usual expression,

$${\mathbb{E}}{\{O(T)\}}_{\rho }={\langle {\rm{tr}}[U(T)(\rho \otimes {\rho }_{B})U{(T)}^{\dagger }O]\rangle }_{c},$$

(3)

where $U(T)={\mathcal{T}}{e}^{-i\mathop{\int}\nolimits_{0}^{T}dsH(s)}$ and ${\left\langle \cdot \right\rangle }_{c}$ denotes classical averaging over the noise realizations of the random process β_α(t), and ρ_B is the initial state of the bath. One can then move to a toggling-frame with respect to the control Hamiltonian H_ctrl(t), inducing a control unitary U_ctrl(T) via,

$${U}_{\text{ctrl}}(T)={{\mathcal{T}}}_{+}{e}^{-i\mathop{\int}\nolimits_{0}^{T}{H}_{\text{ctrl}}(s)ds},$$

(4)

which enables the decomposition,

$$U(T)={\tilde{U}}_{I}(T){U}_{{\rm{ctrl}}}(T),$$

(5)

with,

$${\tilde{U}}_{I}(T)={{\mathcal{T}}}_{+}{e}^{-i\mathop{\int}\nolimits_{0}^{T}{U}_{\text{ctrl}}(T){H}_{I}(s){U}_{\text{ctrl}}^{\dagger }(T)ds},$$

(6)

the (modified) interaction picture evolution (see Supplementary Note 2 for details), and H_I(t) is defined as

$${H}_{I}(t)={U}_{\text{ctrl}}^{\dagger }(t){H}_{1}(t){U}_{\text{ctrl}}(t),\, {H}_{1}(t)={\sum \limits_{\alpha = x,y,z}}{\sigma }_{\alpha }\otimes {B}_{\alpha}(t).$$

(7)

In turn, this allows us to rewrite,

$${\mathbb{E}}{\{O(T)\}}_{\rho }={\rm{tr}}[{V}_{O}(T){U}_{{\rm{ctrl}}}(T)\rho {U}_{{\rm{ctrl}}}{(T)}^{\dagger }O],$$

(8)

where the operator

$${V}_{O}(T)=\left\langle {O}^{-1}{\tilde{U}}_{I}^{\dagger }(T)O{\tilde{U}}_{I}(T)\right\rangle ,$$

(9)

where $\langle \cdot \rangle ={\langle {{\rm{tr}}}_{B}[\cdot {\rho }_{B}]\rangle }_{c}$ conveniently encodes the influence of the noise. As such, this operator is central to understanding the dynamics of the open quantum system. If our objective is, as is common in optimal control protocols and imperative when quantum-technology applications are considered, to minimize the effect of the noise, e.g., via a dynamical decoupling^44,45,46 or composite pulses^47,48, then one needs to determine a set of controls for which V_O → I. Notice that ${\rm{tr}}[O\langle {\tilde{U}}_{I}^{\dagger }O{\tilde{U}}_{I}\rangle ]$ can be interpreted as the “overlap” between the observable O and its time evolved version $\langle {{\tilde{U}}_{I}}^{\dagger }O{\tilde{U}}_{I}\rangle$, which is maximum when the evolution is noiseless. If additionally one wants to implement a quantum gate G, then we further require that ${U}_{\text{ctrl}}\rho {U}_{\text{ctrl}\,}^{\dagger }\to G\rho {G}^{\dagger }$. Regardless of our objective, it is clear that one needs to be able to predict V_O(T) given (i) the actual noise affecting the qubit and (ii) a choice of control. However, realistically the information available about the noise is limited, and by the very definition of an open quantum system is something that cannot typically be measured directly.

Fortunately, this limitation can in principle be overcome by quantum noise spectroscopy (QNS) protocols^{1,2,3,4,5,6,7,8,9,10,11,12,13}. These protocols exploit the measurable response of the qubit to a known and variable control and the noise affecting it, in order to infer information about the noise. The type of accessible information is statistical in nature. That is, without any other information, e.g., about the type of stochastic noise process, the best one can hope to learn are the bath correlation functions $\langle {\beta }_{{\alpha }_{1}}({t}_{1})\cdots {\beta }_{{\alpha }_{k}}({t}_{k})\rangle$. If the QNS protocol is sufficiently powerful to characterize the leading correlation functions and matches the model, in principle the inferred information can be plugged into a cumulant expansion or a Dyson series expansion of V_O(t) to successfully obtain an estimate of the operator for any choice of f_α(t), as desired. This has led to a proliferation of increasingly more powerful QNS protocols, including those capable of characterizing the noise model described here¹⁰, some of which have even been experimentally verified^{1,2,3,4,7,8,13,49,50}. More generally, the idea of optimizing control procedures to a known noise spectrum²² is behind some of the most remarkable coherence times available in the literature⁵¹.

QNS protocols, however, are not free of complications. The demonstrated success of these protocols relies on the assumptions, which support them being satisfied. Different protocols have different assumptions, but they can be roughly grouped into two main flavors:

• Assumptions on the noise—Existing protocols assume that the only a certain subset of the correlation functions effectively influence the dynamics or, equivalently that a perturbative expansion of V_O(t) can be effectively truncated to a fixed order. In practice, this is enforced in various ways. For example, demanding that the noise is Gaussian and dephasing or, more generally, that one is working in an appropriately defined “weak coupling” regime^5,9,11.

• Assumptions on the control— Many QNS protocols, especially those based around the so-called ‘frequency-comb’^2,5,9,10, rely on specific control assumptions, such as that pulses are instantaneous. This assumption facilitates the necessary calculations, which ultimately allow the inferring of the noise information. However, it enforces constraints on the control that translate into limitations on the QNS protocol, e.g., a maximum frequency sampling range^2,5. Moreover, experimentally one cannot realize instantaneous pulses, so comb-based QNS protocols are necessarily an approximation with an error that depends on how far the experiment is from satisfying the instantaneous pulse assumption.

This work overcomes these limitations by bypassing the step of inferring the bath correlation functions. We maintain the philosophy of QNS regarding characterizing the open quantum system dynamics, but pose it in a machine-learning context. Thus, we address the question:

Can an appropriately designed machine-learning algorithm ‘learn’ enough about the open quantum system dynamics (relative to a given set of control capabilities), so as to be able to accurately predict its dynamics under an arbitrary element of the aforementioned set of available controls?

We answer positively to this question by implementing such ML-based approach. Concretely our ML algorithm (i) learns about the open quantum system dynamics and (ii) is capable of accurately estimating—without assuming a perturbative expansion—the operator V_O(T), and consequently measurement outcomes, resulting from a control sequence picked from the family control pulses {f_α(t)} specified by an assumed (but in principle arbitrary) set of control capabilities.

The “Results” section is organized as follows. We start by giving an overall summary of our proposed solution. Next, we present some of the mathematical properties of the V_O operator. This will allow us to find a suitable parameterization that will be useful to build the architecture of the ML model. After that, we present exactly the architecture of the ML model followed by an overview on how to construct datasets in order to train and test the model, as well as the training and testing procedures. Finally, we discuss the numerical implementation of the proposed solution followed by the presenting the numerical results. We show the results of training and testing the ML model, as well as using the trained model to perform dynamical decoupling, quantum control, and quantum noise spectroscopy.

Results

Overview

The ML approach naturally matches our control problem, which becomes clear from the following observation. For most optimal control applications, e.g., achieving a target fidelity for a gate acting on an open quantum system, one does not need to have full knowledge of the noise. To see this consider a hypothetical scenario where the available control is band limited^8,11,52, i.e., whose frequency domain representation F(ω) is compactly supported in a fixed frequency range ∣ω∣ ≤ Ω₀. If the response of the open quantum system to the noise⁵³ is captured by a convolution of the form $I=\mathop{\int}\nolimits_{-\infty }^{\infty }d\omega F(\omega)S(\omega)$, where S(ω) represents the noise power spectrum, then it is clear that one only needs to know S(ω) for ∣ω∣ ≤ Ω₀. While this statement can be formalized and made more general²⁴, the above example captures a key point: only the ‘components’ of the noise that are relevant to the available control need to be characterized. Conversely, this means that a fixed set of resources, e.g., a set of control capabilities, can only provide information about the ‘components’ of the noise relevant to them. The above observations make the ML approach particularly well suited for the problem: it is natural to draw the connection between the control problem of ‘characterizing a system with respect to a restricted set of control capabilities in order to predict the dynamics under any control such capabilities can generate’ and the fact that the training and testing datasets typical in ML make sense when the datasets are generated in the same way, i.e., by the same ‘control capabilities’. Of course, the details of the ML approach that can seamless integrate with the quantum control equations are important, and we now provide them.

In order to address the question presented in the Introduction section, we are going to use an ML graybox-based approach similar to the one presented in³². The basic idea of a graybox is to divide the ML model into two parts, a blackbox part and a whitebox part. The blackbox part is a collection of standard ML layers, such as neural networks (see Supplementary Note 3 for an overview), that allows us to learn maps between variables without any assumptions on the actual relation. The whitebox part is a collection of customized layers that essentially implement mathematical relations that we are certain of. This approach is better than a full blackbox, because it allows us to estimate physically relevant quantities, and thus enables us to understand more about the physics of the system. In other words, the blackboxes are enforced to learn some abstract representations, but when combined with the whiteboxes we get physically significant quantities. In the parlance of machine-learning, these whitebox layers are ‘quantum features’, which extract the expect patterns in the data fed to the network.

In the case of the problem under consideration, we are going to use the blackbox part to estimate some parameters for reconstructing the V_O operators. The reason behind the use of a blackbox for this task is because the calculation of the V_O operators depends on assumptions on the noise and control signals. So, by using a blackbox we get rid of such assumptions. Whereas the whitebox parts would be used for the other standard quantum calculations that we are certain of, such as the time-ordered evolution, and quantum expectations. Thus, we end up with an overall graybox that essentially implements Eq. (8), with input representing the control pulses, output corresponding to the classical expectation of quantum observable over the noise, and internal parameters modeling abstractly the noise and its interaction with the control. With this construction, we would be able to estimate important quantities such as V_O, and U_ctrl. Now, since we are using machine-learning, then we will need to perform a training step to learn the parameters of the blackboxes. Thus, the general protocol would be as follows:

• 1. Prepare a dataset consisting of pairs of random input pulse sequences applied to the qubit (chosen from a fixed and potentially infinite set of allowed sequences), and the measured outcomes after evolution.

• 2. Initialize the internal parameters of the graybox model.

• 3. Train the model for some number of iterations until convergence.

• 4. Fix the trained model and use it to predict measurement outcomes for new pulse sequences, as well as the V_O operators.

It should be noted the nature of quantum information enforces characterization of quantum systems of large dimension to blow-up. This is a common problem in any characterization protocol, including quantum state tomography, quantum process tomography, quantum noise spectroscopy, and even quantum control unless some simplifying assumptions are made. However, in most practical situations, a full characterization may not be required. A full characterization of a set of small subsystems can be sufficient. This is the case for quantum computing where arbitrary multi-qubit quantum gates are compiled into 1- and 2-qubit gates. Alternatively, a partial characterization of the whole system can be sufficient. This is the case for quantum error correction where only a small subset of observables (error syndromes) are of interest. In either case, using the proposed machine-learning framework will remain feasible.

Mathematical properties of the V_O operator

If we look back into the definition of the V_O operator, we find that it is convenient to express it as

$${V}_{O}={O}^{-1}\left\langle {\tilde{U}}_{I}^{\dagger }O{\tilde{U}}_{I}\right\rangle \equiv {O}^{-1}{\langle {W}_{O}\rangle }_{c},$$

(10)

because the observable is independent of the noise. As a result we can see that W_O is a system-only operator with the following properties. Namely, for a given realization of the classical noise process and recalling that O is a traceless qubit-only (system-only) observable, one has that

• 1. The trace of W_O is bounded. This follows by noting that ${\rm{tr}}[{W}_{O}]={{\rm{tr}}}_{S}[O{{\rm{tr}}}_{B}[{\tilde{U}}_{I}({I}_{S}\otimes {\rho }_{B}){\tilde{U}}_{I}^{\dagger }]]={{\rm{tr}}}_{S}[O{\mathcal{E}}({I}_{S})]\in [-1,1],$ where ${\mathcal{E}}(\cdot)={{\rm{tr}}}_{B}[{\tilde{U}}_{I}(\cdot \otimes {\rho }_{B}){\tilde{U}}_{I}^{\dagger }]$ is a Completely-Positive Trace-Preserving map. In the special case where the noise generates a unital channel, i.e., when ${\mathcal{E}}({I}_{S})={I}_{S}$, as is the case for classical-only noise, then ${\rm{tr}}[{W}_{O}]=0,$ since O is a traceless observable.

• 2. W_O is Hermitian. One can see this by noting that W_O can always be written as ${W}_{O}={\sum }_{\alpha = 0,x,y,z}{{\rm{tr}}}_{S}[{\sigma }_{\alpha }{{\rm{tr}}}_{B}[{\tilde{U}}_{I}^{\dagger }O{\tilde{U}}_{I}({I}_{S}\otimes {\rho }_{B})]]\ {\sigma }_{\alpha }/2$. Since ${{\rm{tr}}}_{S}[{\sigma }_{\alpha }{{\rm{tr}}}_{B}[{\tilde{U}}_{I}^{\dagger }O{\tilde{U}}_{I}({I}_{S}\otimes {\rho }_{B})]]={{\rm{tr}}}_{SB}[O{\tilde{U}}_{I}({\sigma }_{\alpha }\otimes {\rho }_{B}){\tilde{U}}_{I}^{\dagger }]={{\rm{tr}}}_{S}[O{\mathcal{E}}({\sigma }_{\alpha })]={{\rm{tr}}}_{S}[O\left(\right.{\mathcal{E}}(\frac{{I}_{S}+{\sigma }_{\alpha }}{2})-{\mathcal{E}}(\frac{{I}_{S}-{\sigma }_{\alpha }}{2})]\in {\mathbb{R}},$ it follows that ${W}_{O}={W}_{O}^{\dagger }$.

• 3. Given the above and observing that ${{\rm{tr}}}_{S}[{\sigma }_{\alpha }{W}_{O}]={{\rm{tr}}}_{S}[O{\mathcal{E}}({\sigma }_{\alpha })]\in [-1,1],$ it follows that W_O has real eigenvalues λ₁, λ₂ ∈ [− 1, 1].

If one also considers the effect of the average over realizations of the stochastic process, one further finds that the full average (including classical and quantum components) satisfies the following properties

• 1. Its trace is bounded, i.e., ${\rm{tr}}[{\left\langle {W}_{O}\right\rangle }_{c}]\in [-1,1]$.

• 2. It is Hermitian, i.e., ${\langle {W}_{O}\rangle }_{c}^{\dagger }={\langle {W}_{O}^{\dagger }\rangle }_{c}={\langle {W}_{O}\rangle }_{c}.$

• 3. Since for any realization W_O has real eigenvalues in [− 1, 1], the average over realizations of that process will also have that property, i.e., its eigenvalues are such that $-1\,\le \,\lambda ({\langle {W}_{O}\rangle }_{c})\,\le \,1$. This can be proved as follows. Suppose for the sake of convenience that the probability distribution of the W_O with respect to the noise is finite and discrete. That is it can only take values ${\tilde{W}}_{i}$ with probability _Pi. Then

  $${\lambda }_{\max }\left({\left\langle {W}_{O}\right\rangle }_{c}\right)={\lambda }_{\max }\left(\mathop{\sum }\limits_{i = 1}^{{i}_{\max }}{P}_{i}{\tilde{W}}_{i}\right)$$

  (11)
  $$={\lambda }_{\max }\left({P}_{1}{\tilde{W}}_{1}+\mathop{\sum }\limits_{i = 2}^{{i}_{\max }}{P}_{i}{\tilde{W}}_{i}\right)$$

  (12)
  $$\le {\lambda }_{\max }\left({P}_{1}{\tilde{W}}_{1}\right)+{\lambda }_{\max }\left(\mathop{\sum }\limits_{i = 2}^{{i}_{\max }}{P}_{i}{\tilde{W}}_{i}\right)$$

  (13)
  $$={P}_{1}{\lambda }_{\max }\left({\tilde{W}}_{1}\right)+{\lambda }_{\max }\left(\mathop{\sum }\limits_{i = 2}^{{i}_{\max }}{P}_{i}{\tilde{W}}_{i}\right)$$

  (14)
  $$\le {P}_{1}+{\lambda }_{\max }\left(\mathop{\sum }\limits_{i = 2}^{{i}_{\max }}{P}_{i}{\tilde{W}}_{i}\right).$$

  (15)

  The third line follows from Weyl’s inequality since all the terms of the form ${P}_{i}\tilde{{W}_{i}}$ are Hermitian. Now, if we repeat recursively the same steps on the second remaining term, we get

  $${\lambda }_{\max }\left({\left\langle {W}_{O}\right\rangle }_{c}\right)\le {P}_{1}+{P}_{2}+\cdots {P}_{{i}_{\max }}$$

  (16)
  $$=1,$$

  (17)

  as the P_i’s form a probability distribution. Similarly, we can show that

  $${\lambda }_{\text{min}}\left({\left\langle {W}_{O}\right\rangle }_{c}\right)\ge {\lambda }_{\text{min}}\left(\mathop{\sum }\limits_{i = 1}^{{i}_{\max }}{P}_{i}{\tilde{W}}_{i}\right)$$

  (18)
  $$\ge -1.$$

  (19)

  and so by combining the two results we get

  $$-1\le \lambda \left({\left\langle {W}_{O}\right\rangle }_{c}\right)\le 1$$

  (20)

This proof can be extended to the more realistic situation when the noise distribution is continuous. Thus, by specifying a diagonal matrix D whose entries are real numbers in the interval [−1, 1] adding up to a number that lies in the [−1, 1], and by choosing a general unitary matrix Q, we can reconstruct any V_O operator in such a way that satisfies its mathematical properties, using the eigendecomposition

$${V}_{O}=\left\langle {O}^{-1}{U}_{I}^{\dagger }O{U}_{I}\right\rangle ={O}^{-1}QD{Q}^{\dagger }.$$

(21)

In particular for the case of qubit presented in this paper (i.e., d = 2), we can completely specify the V_O operator using six parameters, which we would refer to as ψ, θ, Δ, λ₁, and λ₂ such that

$$Q=\left(\begin{array}{ll}{e}^{i\psi }&0\\ 0&{e}^{-i\psi }\end{array}\right)\left(\begin{array}{ll}\cos \theta &\sin \theta \\ -\sin \theta &\cos \theta \end{array}\right)\left(\begin{array}{ll}{e}^{i\Delta }&0\\ 0&{e}^{-i\Delta }\end{array}\right),$$

(22)

where we neglected a degree of freedom that represents an overall global phase shift, and

$$D=\left(\begin{array}{ll}{\lambda }_{1}&0\\ 0&{\lambda }_{2}\end{array}\right),$$

(23)

satisfying ∣Λ∣ = ∣λ₁ + λ₂∣ ≤ 1. The parameters ψ, θ, and Δ can take any real values as they are arguments of periodic functions.

In this paper we will focus on the unital case, i.e., λ₁ + λ₂ = 0, since we will validate our ML approach via simulated experiments using classical-only noise. In this case, we we can write the eigenvalue matrix as

$$D=\left(\begin{array}{ll}\mu &0\\ 0&-\mu \end{array}\right),$$

(24)

and μ ∈ [0, 1]. In what follows, when building our ML machinery, we will specify how this constraint is implemented and how it can be obviated in each layer. Note that in an actual experiment, where no assumption on the classicality of the noise is valid a priori, the general, non-unital, case should be considered.

Model architecture

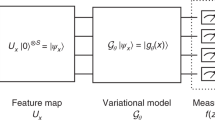
The proposed graybox ML model is shown in Fig. 1. We shall explain in detail the structure as follows.

Fig. 1: The proposed graybox architecture for modeling the noisy qubit following Eq. (8).

The inputs of the model are the sequence of control signal parameters {α_n}, and the actual time-domain waveform f(t). The outputs of the model are the expectations over the noise for all the Pauli eigenstates as initial states, and all Pauli’s as measurement operators. The blackbox part of the model consist of two layers of GRU followed by a neuron layer. The output of this layer represents the parameters that can be used to construct the “V_O” operator. There are three different branches corresponding to each of the three possible Pauli observables. The whitebox part of the model is formed from the layers that implement specific formulas known from quantum mechanics. This includes layers for constructing the V_O operators from the parameters generated from the blackbox, constructing the control Hamiltonian from the time-domain representation of the control pulse sequence, the time-ordered evolution to generate the control unitary, and the quantum measurement layer. The model is trained using a set of pairs of control pulse sequence and corresponding expectation values of the observables. After training, the model can be used to predict the measurements for new pulse sequences. It can also be probed to estimate one of the “V_O” operators, and thus can be used as a part of a quantum control algorithm to achieve a desired quantum gate.

The purpose of the proposed architecture is to have a model that relates the control pulses applied on the qubit (which we have control over in an experiment) to the classical average of the quantum observables (which we can physically measure). The model internal parameters will act as an abstract representation for the noise, as well as how it affects the measurement outcomes. The model inputs represents different “features” extracted from the control pulse sequence. In this paper, we make use of two independently processed features, and thus the model has two inputs. The first feature is a global feature of the control pulse: the parameterization of the pulse. The other is a local feature: the time-domain representation of the pulse. These two features are explained as follows.

The first feature represents the set of parameters defining the control pulse sequence. We assume in this paper that the control signal can be parameterized by a finite set of parameters. This still allows having infinitely large number of possible control signals since each of the parameters can take infinitely many values. For example a train of N Gaussian pulses can be completely defined by 3N parameters: the amplitude, mean, and variance of each of the N pulses. Similarly, a train of square pulses can be defined by each of the pulse positions, pulse widths, and pulse amplitudes. Now, these parameters have to be represented in a way that is suitable for the subsequent blocks (standard ML blackboxes) to process. So, the first step is to normalize each of signal parameters to be in the range of [0, 1] across all the examples. For instance, the pulse locations can be normalized with respect to the the total evolution time T since there will be no pulses beyond this point in time. The pulse amplitudes could also be normalized such that the maximum amplitude for any pulse sequence is 1. The second is step is the proper formatting of these parameters. We choose to organize the signal parameters of an ${n}_{\max }$ pulse train in the form of a sequence of vectors ${\{{{\boldsymbol{\alpha }}}_{n}\}}_{n = 1}^{{n}_{\max }}$, where each vector represents the n^th pulse and has r entries representing the normalized pulse parameters (example: Gaussian pulse train will have r = 3). For the case of multi-axis control, we concatenate the parameterization along each direction into one vector assuming the controls are independent along each direction. We emphasize here that we take Gaussian and square pulses as examples to demonstrate our ideas, but in general any waveform with any suitable parameterization could be used. This feature is considered global since every parameter affects the whole waveform shape of control sequence.

The second feature used for the model is the actual time-domain representation of the pulse sequence, discretized into M steps. In other words, the amplitude of the pulse at each time step. This feature is considered local, since a change in one of the parameters does not affect the whole sequence. This input is only processed by customized whiteboxes. Although in principle we can calculate the time-domain representation from the signal parameters in the first input, it turns out that the overall algorithm performs better if we do not do this calculation directly. In other words treat both features as two “independent inputs” to the model.

The output of the model should be the measurement outcomes. If we initialize our qubit to each of the eigenstates (“up/down”) of each Pauli operators (that is a total of 6 states), and measure the three Pauli operators, then we have enough information (tomographically complete) to predict the dynamics for other configurations. So, we need to perform a total of 18 “prepare-measure” experiments and collect their results. Moreover so, our model will have 18 outputs corresponding to each of the measurement settings.

As discussed previously, there are lots of known relations from quantum mechanics that we are certain of. It is better in terms of the overall performance to directly implement as much as possible of these relations in non-standard customized layers. This saves the machine from essentially having to learn everything about quantum mechanics from the data, which would be hard and could decrease the overall accuracy. Moreover, this allows us to evaluate physically significant quantities, which is one of the most important general advantages of the graybox approach. In our proposed model, we make use of the following whiteboxes.

• Hamiltonian construction: this layer takes the discretized time-domain representation of the control pulses (which is exactly the second input to the model), and outputs the control Hamiltonian H_ctrl evaluated at each of the M time steps using Equation (2). The layer is also parameterized by the energy gap Ω, which we fix at the beginning.

• Quantum evolution: this layer follows the “Hamiltonian Construction” layer, and thus it takes the control Hamiltonian at each time step as input and evaluates the time-ordered quantum evolution as output (i.e., Eq. (4)). Numerically, this is calculated using the approximation of an infinitesimal product of exponentials

  $${U}_{\text{ctrl}}={{\mathcal{T}}}_{+}{e}^{-i\mathop{\int}\nolimits_{0}^{T}{H}_{\text{ctrl}}(s)ds}$$

  (25)
  $$=\mathop{\rm{lim}}\limits_{M\to \infty }{e}^{-i{H}_{\text{ctrl}}({t}_{M})\Delta T}{e}^{-i{H}_{\text{ctrl}}({t}_{M-1})\Delta T}\cdots {e}^{-i{H}_{\text{ctrl}}({t}_{0})\Delta T}$$

  (26)
  $$\approx {e}^{-i{H}_{\text{ctrl}}({t}_{M})\Delta T}{e}^{-i{H}_{\text{ctrl}}({t}_{M-1})\Delta T}\cdots {e}^{-i{H}_{\text{ctrl}}({t}_{0})\Delta T},$$

  (27)

  where t_k = kΔT and $\Delta T=\frac{T}{M}$. The last line follows if M is large enough.

• V_O construction: this layer is responsible for reconstructing the V_O operator. It takes the parameters ψ, θ, Δ, and μ as inputs and outputs the V_O following the reconstruction discussed previously. The blackboxes of the overall model are responsible for estimating those parameters. The output of this layer can be probed to estimate the V_O operator given a control pulse. This allows us to do further operations, including noise spectroscopy and quantum control. In the general case for non-unital dynamics, the reconstruction will require the two parameters λ₁ ∈ [−1, 1] and Λ = λ₁ + λ₂ ∈ [−1, 1], instead of the parameter μ ∈ [0, 1].

• Quantum measurement: this layer is essentially the implementation of Eq. (8). So, it takes the V_O operator as input, together with the control unitary, and outputs the trace value. It is parameterized by the initial state of the qubit, as well as the observable to measure. Therefore, in order to calculate all possible 18 measurements, we need 18 of such layers in the model, each with the correct combination of inputs and parameterization. The outputs of all 18 layers are concatenated finally and they represent the model’s output.

The exact calculation of the measurement outcomes requires assumptions on both the noise and control pulse sequence. So, by using the standard ML blackbox layers, such as neural networks (NN) and gated reccurent units (GRU) (see Supplementary Note 3 for an overview), we can have an abstract assumption-free representation of the noise and its interaction with the control. This would allow us to estimate the required parameters for reconstructing the V_O operators using a whitebox. The power of such layers comes from their effectiveness in representing unknown maps due to their highly non-linear complex structure. In our proposed model we have three such layers explained as follows.

• Initial GRU: this layer is connected to the first input of the model, i.e., the parameters of the control pulse sequence. The purpose behind this layer is to have an initial pre-processing of the input features. Feature transformation is commonly used in ML algorithms, to provide a better feature space that would essentially enhance the learning capability of the model. In the modern deep learning paradigm, instead of doing feature transformation at the beginning, we actually integrate it within the overall algorithm. In this way, the algorithm learns the best optimal transformation of features that increases the overall accuracy. In our application, the intuition behind this layer is to have some sort of abstract representation of the interaction unitary U_I. This would depend on the noise, as well as the control. In this sense, the input of the layer represents the control pulses, the output represents the interaction evolution operator, and the weights of the layer represent the noise. This does not mean that probing the output layer is exactly related to the actual U_I as the algorithm might have a completely different abstract representation, which is a general feature of blackboxes. In the proposed model, we choose the GRU unit to have ten hidden nodes. The reason behind choosing the GRU, which is a type of a recurrent neural network (RNN), rather than a standard neural network, is to make use of the feedback mechanism. We would like to have a structure that processes a sequence not only term by term, but taking into account previous terms. An RNN-like structure would accomplish this kind of processing. In this sense, we can abstractly model relations that involve convolution operations, which is exactly the type of relations obtained when we do theoretical calculations of the dynamics of open quantum systems.

• Final GRU: this is another GRU layer that is connected to the output of the initial GRU layer. The purpose of this layer is to increase the complexity of the blackboxes so that the overall structure is complex enough to represent our relations. For our application, this layer serves as a way to estimate the operator $\langle {U}_{I}^{\dagger }O{U}_{I}\rangle$ in some abstract representation. Moreover, thus we need actually three of such layers to correspond to the three Pauli observables. We choose to have 60 hidden nodes for each of these layers.

• Neural network: this is a fully connected single neural layer consisting of four nodes. The output of the final GRU layer is connected to each of the nodes. The first three nodes have linear activation function and their output represent the actual parameters ψ, θ, and Δ that are used to construct the V_O operator. The last node has a sigmoid activation function and its output corresponds exactly to the μ parameter of the V_O operator. As discussed before the μ parameter has to be in the range [0, 1], which is exactly the range of the sigmoid function. Since the parameters will differ for each of the three observables, we need three of such layers each connected to one of the final GRU layers. In the case of non-unital dynamics, the neural network will change as follows. First, the fourth node will have a hyperbolic tangent (tanh) activation (whose range is [−1, 1]) and would represent the parameter λ₁ instead of μ. Second, a fifth node with a hyperbolic tangent activation will be needed to represent the parameter Λ. In this way, the constraints of the V_O operators will be satisfied, and hence the architecture would be suitable for modeling the non-unital dynamics.

Dataset construction

For any ML algorithm, we need a dataset for training it and testing its performance. A dataset is a collection of “examples” (instances), where each example is a pair of inputs (that should be fed to the algorithm) and corresponding actual outputs or “labels” (that the algorithm is required to predict). The dataset is usually split into two parts, one part is used for training the algorithm while the other part is used for testing its performance. The examples belonging to the testing portion of the dataset are not used in the training process at all. In the application presented in this paper, the dataset would be a collection of control pulse sequences applied to a quantum system, and the corresponding measured quantum observables. In the experimental situation such a dataset can be constructed as follows. We prepare the qubit in an initial state, apply some a control sequence, then measure the observable. This is repeated for all 18 possible configurations of initial states/observables. The pair consisting of the control pulse sequence parameterization and time-domain representation, and the value of the 18 measurements would correspond to one example in the dataset. To generate more examples, we choose different control sequences and repeat the whole process. In this paper, we do not have access to an actual experiment. However, we need to validate the proposed algorithm, so we generate datasets by computer simulation of a noisy qubit (details are given later in this section, and also in Supplementary Note 1). In a practical application of the algorithm with experimental data, there is no need to use simulated datasets. The algorithm will be trained directly from the acquired data.

An important aspect of this discussion is how to choose the examples constituting the dataset and how large the dataset should be. This is an empirical process, but there are general principles to follow. First, any ML algorithm should be able to generalize, i.e., predict the outcomes for examples that were not in the training portion of the dataset. The way to ensure this is to have the training subset large enough to represent wide range of cases. For instance, consider constructing a dataset of CPMG-like sequences⁵⁴, i.e., sequences composed of equally spaced pulses. Then, in order for the model to have the capability of predicting the correct outcomes if the pulses are shifted (maybe due to some experimental errors), we have to provide training examples in which the control pulses are randomly shifted. Similarly, if we want accurate predictions for control pulses that have powers other than π, then we need to include such examples for training. Additionally, the prediction would work for example of the same pulse shape. This means that if all training examples are square pulses then the predictions would be accurate only for square pulses. In case we need the trained algorithm to predict outcomes corresponding to pulses of different shapes, then we must include examples of all desired shapes in the dataset (for example, square and Gaussian pulses). This would result in an increase in the complexity of training due to two reasons. First, more computations will be required as we have to increase the size of the dataset to include examples of the different pulse shapes. The second reason is that consequently we need to increase the learning capacity of the blackboxes (by increasing the number of nodes in the neural networks, GRU’s,...etc.). However, this is not a problem in practice specially in actual physical experiments. The reason is that usually there are constraints about what types of control sequences can be generated. This would depend on the specifications of the available hardware in the experiment. For example, it might be only possible to generate square pulses with some maximum amplitude, or Gaussian pulses with a fixed pulse duration. In such cases, we will be interested to predict and control the dynamics of a quantum system driven by that particular kind of pulses only. Therefore, the dataset needs to consist of examples of control sequences whose pulse shape is of interest. This would result in a smaller dataset and the training complexity decreases. Thus, experimental constraints arising from the specifications of the available hardware defines what control capabilities are available, which in turn simplifies the process of training the ML algorithm. In this paper, we do not consider training the algorithm on datasets consisting of different pulse shapes. However, we construct different datasets and train different ‘instances’ of the algorithm on each dataset independently. This is done for the purpose of proving the concept, and showing that the proposed algorithm works with different pulse shapes. Later in this section, we give details about the different datasets we constructed in this paper, as well as the results of training and testing the algorithm on each of the datasets individually.

The size of the dataset (i.e., the number of instances) is usually chosen empirically. The general rule of thumb is that the more training examples are used, the better the generalization of the algorithm is. Moreover, the more testing examples are used in the assessment process, the better the assessment is. So, usually the procedure is iterative where we start with some size for the dataset, train the algorithm, assess the performance, and then decide whether the size is sufficient or not. Note, however, that we might be constrained by some upper limit on the dataset size before the process of data collection becomes infeasible. This is one of the main challenges facing the design of modern ML algorithms.

Training and testing

The second step after constructing the dataset, is to choose a loss function for the model. This a function that measures how accurate the outputs predicted by the model compared to the true outputs. This choice depends on the application under consideration. In our case, we shall use the mean-square-error (MSE), averaged over all 18 measurement outcomes. The weights of the model are chosen such that the loss function is minimized. Ideally, we seek a global minimum of the loss function but in practice this might be hard and we probably end up with a local minimum. However, practically, this usually provides sufficient performance.

The third step is to choose an optimization algorithm. The optimization is for finding the weights of the model that minimizes the loss function averaged over all training examples. The standard method used in ML is backpropagation that is essentially a gradient descent-based method combined with an efficient way of calculating the gradients of the loss function with respect to the weights. There are many variants of the backprogation method in the literature, the one we choose to use in this paper is the Adam algorithm⁵⁵. There exist also other gradient-free approaches such as genetic algorithm (GA)-based optimization³⁹.

The fourth step is to actually perform the training. In this case, we initialize the weights of the model to some random values, then apply enough iterations of the optimization algorithm till the loss function reaches a sufficiently small value. In the case of MSE, we would like it ideally to be as close as possible to 0, but this could require infinite number of iterations. So, practically we stop either when we reach sufficient accuracy or we exceed a maximum number of steps.

A final thing to mention is that because the whiteboxes do not have any trainable parameters, the blackboxes are enforced through the training to generate outputs that are compatible with the whiteboxes, so that we end up with the correct physical quantities.

After executing the aforementioned steps for training the algorithm, it will be able to predict accurately the outputs of the training examples. In our application, this by itself is useful because we can easily probe the output of the V_O layers and use that prediction for various purposes. However, we have to ensure the model is also capable of generalizing to new examples. This is where the portion of the dataset used for testing comes in place. The trained algorithm is used to predict the outcomes of the control pulse sequences of the testing subset, and the average MSE is calculated. Next, the testing MSE is compared to the training MSE. If the testing MSE is sufficiently low then this indicates the model has good predictive power. Ideally, we need the MSE of the testing subset to be as close as possible to the MSE of the training subset. Sometimes this does not happen and we end up with the testing MSE being significantly higher than that of the training MSE. This is referred to as overfitting. In order to diagnose this behavior we usually plot the MSE of both subsets evaluated at each training iteration on the same axes, versus the iteration number. Note, that the testing examples or the testing MSE do not contribute at all to the training process of the algorithm, they are just used for performance evaluation. If both curves decrease as the number of iterations increase, until reaching a sufficiently low level, then the model has a good fit. If the testing MSE saturates eventually or worse starts increasing again, then the algorithm is overfitting. There are many methods proposed in the classical machine-learning literature to overcome overfitting, including decreasing the model complexity, increasing the number of training examples, and early stopping (i.e., stop the iterations before the testing MSE of the testing starts to increase). On the other hand, the significance of overfitting on the performance of a model depends on the application, and the required level of accuracy. This means that a model might be experiencing some overfitting behavior, but the prediction accuracy is still sufficient.

Implementation

We implemented the proposed protocol using the “Tensorflow” Python package⁵⁶, and its high-level API package “Keras”⁵⁷. We also implemented a simulator of a noisy qubit, to generate the datasets for training and testing. It simulates the dynamics of the qubit using Monte Carlo method rather than solving a master equation, to be general enough to simulate any type of noise. The details of the design and implementation of this simulator are presented in Supplementary Note 1. We chose the simulation parameters as shown in Table 1.

Table 1 The different simulation parameters used for generating the datasets.

We created three categories of datasets using the simulator, summarized in Table 2, as follows.

• 1. Qubit with noise on a single-axis and control pulses on an orthogonal axis.

  The Hamiltonian in this case takes the form

  $$H=\frac{1}{2}\left(\Omega +{\beta }_{z}(t)\right){\sigma }_{z}+\frac{1}{2}{f}_{x}(t){\sigma }_{x}.$$

  (28)

  We chose the noise to have the following power spectral density (PSD) (single-side band representation, i.e., the frequency f is non-negative)

  $${S}_{Z}(f)=\left\{\begin{array}{ll}\frac{1}{f+1}+0.8{e}^{-\frac{{(f-20)}^{2}}{10}}&0\,< \,{f}\,\le \,{50}\\ 0.25+0.8{e}^{-\frac{{(f-20)}^{2}}{10}}&{f}\,>\,{50}\end{array}\right.$$

  (29)

  Figure 2a shows the plot of this PSD. The reason for choosing such a form is to ensure that the resulting noise is general enough, while also covering some special cases (such as 1/f noise). Also, the total power of the noise is chosen such the effect of noise is evident on the dynamics (i.e., having coherence < 1). In this category, we generated two datasets. The first one is for CPMG pulse sequences with Gaussian pulses instead of the ideal delta pulses. So, the control function takes the form

  $$f(t)=\mathop{\sum }\limits_{n = 1}^{{n}_{\max }}A{e}^{-\frac{{(t-{\tau }_{n})}^{2}}{2{\sigma }^{2}}},$$

  (30)

  where $\sigma =\frac{6T}{M}$, and $A=\frac{\pi }{\sqrt{2\pi {\sigma }^{2}}}$, and ${\tau }_{n}=\left(\frac{{n}\,-\,{0.5}}{{n}_{\max }}\right)T$. The highest order of the sequence was chosen to be ${n}_{\max }=28$. Now, this means we have a set of 28 examples only in the dataset. In order to introduce more examples in the dataset, we randomize the parameters of the signal as follows. The position of the n^th pulse of a given sequence is randomly shifted by a small amount δ_τ chosen at uniform from the interval [−6σ, 6σ]. As a result, we lose the CPMG property that all pulses are equally spaced. However, this can be useful experimentally when there is jitter noise on the pulses. Additionally, we also randomize the power of the pulse. In this case, we vary the amplitude A by scaling it with randomly by amount δ_A chosen at uniform from the interval [0, 2]. For this randomization, we scale all the pulses in the same sequence with the same amount. Again we lose the property of CPMG sequences that they are π- pulses, but this is needed so that the algorithm can have sufficient generalization power. With these two sources of randomness, we generate 100 instances of the same order resulting in a total of 2800 examples. Finally, we split randomly the dataset following the 75:25 ratio convention into training and testing subsets.

  Fig. 2: Powers spectral density of the noise signals that were used to generate the datasets in categories 1 and 2.

  

  The plot in a is for S_Z(f) and the plot in b is for S_X(f).

  The second dataset in this category is very similar with the only difference being the shapes of the pulses. Instead of Gaussian pulses we have square pulses with finite width. The control function takes the form

  $$f(t)=\mathop{\sum }\limits_{n = 1}^{{n}_{\max }}Au(t-{\tau }_{n}-0.5\sigma)u({\tau }_{n}+0.5\sigma-t),$$

  (31)

  where u(⋅) is the Heaviside unit step function, $\sigma =\frac{6T}{M}$, and $A=\frac{\pi }{\sigma }$. The same scheme for randomization and splitting is used in this dataset.

• 2. Qubit with multi-axis noise, and control pulses on two orthogonal directions.

  The Hamiltonian in that category takes the form

  $$H=\frac{1}{2}\left(\Omega +{\beta }_{z}(t)\right){\sigma }_{z}+\frac{1}{2}\left({f}_{x}(t)+{\beta }_{x}(t)\right){\sigma }_{x}+\frac{1}{2}{f}_{y}(t){\sigma }_{y}$$

  (32)

  We chose the noise along z-axis to have the same PSD as in Eq. (33), while the noise along the x-axis has the PSD

  $${S}_{X}(f)=\left\{\begin{array}{ll}\frac{1}{{(f+1)}^{1.5}}+0.5{e}^{-\frac{{(f-15)}^{2}}{10}}&{0}\,< \,{f}\, \le \,{20}\\ (5/48)+0.5{e}^{-\frac{{(f-15)}^{2}}{10}}&{f}\,>\,{20}\end{array}\right.$$

  (33)

  Figure 2b shows the plot of this PSD. This category consists of two datasets. The first one consists of CPMG sequences of maxmimum order of 7 for the x- and y- directions. We take all possible combinations of orders along each direction. This leaves us with 49 possible configurations. We follow the same randomization scheme discussed before applied to the pulses along the x- and y-directions separately. We generate 100 examples per each configuration and then split into training and testing subsets. The second dataset is similar with the only difference that the we do not randomize over the pulse power, we just randomize over the pulse positions.

• 3. Qubit without noise (i.e., a closed quantum system), and pulses on two orthogonal directions.

  The Hamiltonian takes the form

  $$H=\frac{1}{2}\Omega {\sigma }_{z}+\frac{1}{2}{f}_{x}(t){\sigma }_{x}+\frac{1}{2}{f}_{y}(t){\sigma }_{y}$$

  (34)

  This category has only datasets as well which follow the same scheme of pulse configuration and randomization as the second category dataset. The only difference is that the absence of noise.

Table 2 The datasets generated by computer simulations of a noisy qubit for training and assessing the performance of the proposed machine-learning algorithm.

It is worth emphasizing here that since we are generating the datasets by simulation, we had to arbitrarily chose some noise models and pulse configurations. In a physical experiment however, we do not assume any noise models and just directly measure the different outcomes. Moreover, the pulse configurations should be chosen according to the capability of the available experimental setup.

Numerical results

The proposed algorithm was trained on each of the different datasets to assess its performance in different situations. The number of iterations is chosen to be 3000. Table 3 summarizes the MSE evaluated at the end of the training stage for both training and testing examples. Figure 3 shows the history of the training procedure for each of the datasets. The plot shows the MSE evaluated after each iteration for both the training and testing examples. For the testing examples, the MSE evaluated is just recorded and does not contribute to the calculation of the gradients for updating the weights. Figure 4 shows a violin plot of the MSE compared across the different datasets; while Supplementary Figure 2 shows the boxplot. Supplementary Figures 3 to 8 show the square of the prediction errors for measurement outcome in the best case, average case, and worst-case examples of the testing examples of each dataset.

Table 3 The average MSE evaluated for the various datasets at the end of the training process.

Fig. 3: The average MSE evaluated for the training and testing examples versus the iteration number for the various datasets.

The first row is for a CPMG_G_X_28 and b CPMG_S_X_28. The second row is for c CPMG_G_XY_7 and d CPMG_G_XY_pi_7. The final row is for e CPMG_G_XY_7_nl and f CPMG_G_XY_pi_7_nl. The plots show a “good fit” model since both lines are close for each datasets, and they are decreasing as the number of iterations increase. The small fluctuations at the end of the plots result from the gradients of the loss function being noisy, and are exaggerated due to the logarithmic scale of the plot.

Fig. 4: Comparison between the MSE of the various datasets at the end of the training phase, evaluated over the testing subsets only.

The plot depicts an empirical kernel density estimate of data distribution, which is referred to as a Violin plot. The bottom horizontal line represents the minimum value, the middle line represents the median, and the top line represents the maximum. The plot shows how the data is “concentrated” with respect to its order statistics.

Dynamical decoupling and quantum control

For the model trained on the single-axis Gaussian dataset CPMG_G_X_28, we tested the possibility of using it perform some quantum control tasks. Particularly, we implemented a simple numerical optimization-based controller that aims to find the optimal set of signal parameters to achieve some target quantum gate G. We used the cosine similarity as an objective function, which is defined for two d × d matrices U and V as

$$\tilde{F}(U,V)={\left|\frac{{\rm{tr}}[{U}^{\dagger }V]}{\sqrt{{\rm{tr}}[{U}^{\dagger }U]{\rm{tr}}[{V}^{\dagger }V]}}\right|}^{2},$$

(35)

satisfying that $0\le \tilde{F}(U,V)\le 1$. This is a generalized definition for fidelity that reduces to the standard definition of gate fidelity when U and V are unitary,

$$F(U,V)=\frac{1}{{d}^{2}}| {\rm{tr}}[{U}^{\dagger }V]{| }^{2}.$$

(36)

Ideally, we target four objectives listed as follows:

$$\tilde{F}({V}_{O},I)=1,\ \forall O\in \{X,Y,Z\}$$

(37)

$$\tilde{F}({U}_{\text{ctrl}},G)=1,$$

(38)

where V_O and U_ctrl are estimated from the trained model. The first three conditions are equivalent to getting rid of the effects of noise, while the last one is equivalent to having achieve evolution described by quantum gate G. Practically, it is hard to completely remove the noise effects, so what we want to do is to find the set of optimal pulse parameters $\{{{\boldsymbol{\alpha }}}_{n}^{* }\}$ such that

$${\boldsymbol{\alpha}}^{\ast}=\mathop{\arg \min }\limits_{{\boldsymbol{\alpha }}}{(\tilde{F}({V}_{X}[{\boldsymbol{\alpha }}],I)-1)}^{2}+{(\tilde{F}({V}_{Y}[{\boldsymbol{\alpha }}],I)-1)}^{2}+{(\tilde{F}({V}_{Z}[{\boldsymbol{\alpha }}],I)-1)}^{2}+{(\tilde{F}({U}_{\text{ctrl}}[{\boldsymbol{\alpha }}],G)-1)}^{2}.$$

(39)

Then using this objective function we can numerically find the optimal pulse sequence. Utilizing this formulation allows us to treat the problem of dynamical decoupling exactly the same, with G = I. It is important to mention that this is just one method to do quantum control, which might have some drawbacks because of its multi-objective nature. For instance, the optimization could result in one or more of the objectives having sufficient performance, while the others are not. An example of this case is where U_ctrl becomes so close to G, while the V_O operators are still far from the identity. This means that the overall evolution will not be equivalent to G. There are ways to overcome this problem. For example, we can optimize over the observables instead of the operators or optimize over the overall noisy unitary U. However, this is a separate issue, and we defer it to the future work of this paper. We present these results as a proof of concept that it is possible to use the trained model as a part of a quantum control algorithm. We tested this idea to implement a set of universal quantum gates for a qubit. The resulting fidelities are shown in Table 4. The control pulses obtained from the optimization procedures are shown in Fig. 5 and Supplementary Fig. 9.

Table 4 The resulting generalized infidelity between the predicted and target operators using the trained machine-learning model.

Fig. 5: The control pulses to implement some examples of quantum gates.

The plot in a is for the identity (G = I) gate, and the plot in b is for the Pauli X gate (G = X). The pulses are obtained by numerical optimization of the cost function taken to be the average of the generalized infidelity between the V_X, V_Y, V_Z, and U_ctrl and the target operators I, I, I, and G, respectively. The trained model of the CPMG_G_X_28 dataset is utilized.

Quantum noise spectroscopy

It is also possible to use the trained model to estimate the PSD of the noise using the standard Alvarez-Suter (AS) method². In this case, we use the trained model to predict the coherence of the qubit (that is the expectation of the X observable for the X + initial state ${\mathbb{E}}{\{X(T)\}}_{\rho = X+}$) for a set of CPMG sequences at the correct locations and powers. Then, from the predicted coherence we can find the power spectrum that theoretically produces these values. In order to do so we have to assume the noise is stationary and Gaussian. Here, we have trained a separate model with CPMG sequences up to order 50. Since the evolution time T is fixed, the higher the order of the sequence is, the higher the accuracy of the estimated spectrum would be specially at high frequencies. On the other hand, because the pulses still have finite width, there is a maximum we could apply during the evolution time and thus we can only probe the spectrum up to some frequency. Figure 6 shows the plot of the estimated PSD of the noise versus the theoretical one, as well as the coherences obtained from predictions of the model, as well as the theoretical ones. We emphasize here that the point of presenting this work is to develop a method that is more general than the standard QNS method. However, we show in this application that we can still utilize the conventional methods combined with our proposed one. Also, in this experiment the focus was on showing the possibility of doing spectrum estimation. We did not use the trained models discussed in the previous section as they are limited to 28 pulses, which prevents the probing of the spectrum using the AS method to high frequencies.

Fig. 6: The estimated and actual theoretical coherence measurements and noise power spectrum using model trained on the CPMG_G_X_28 dataset.

The plot in a is for the coherences, while the plot in b is for the power spectrum. 50 CPMG sequences with finite width pulses were used to measure the Pauli X observable with the positive Pauli X eigenstate as initial state. The power spectrum is reconstructed using Alvarez-Suter method using the predicted coherences from the trained model.

Discussion

The plots presented in the “Results” section are useful to assess the performance of the proposed method. First, we can see that for all datasets, the average MSE curve evaluated over the training examples versus iterations decreases on average with the number of iterations. This means that the structure is able to learn some abstract representation of the each of the V_O operators as function of the input pulses. For the testing subsets, we see that the MSE curves goes down following the training MSE curves. This indicates that the model is able to predict the observables for the training and testing examples, and thus the fitting is good.

Second, the violin plot and boxplot of the MSE of the testing subsets show that there exists some minor outliers, which we would expect anyway from a machine-learning-based algorithm. However, most of the points are concentrated at or below the median. This indicates that for most testing examples, the prediction was accurate (Note, the lower the MSE the better the prediction is). The best performing cases of the algorithm in terms of the spread of the testing MSE around the median was category 3 datasets. This is expected since in that category the quantum system is closed. Category 2 datasets had a slightly higher median compared to category 1 datasets. This can be explained due to the fact that in category 2, the qubit had multi-axis noise, which means the overall noise strength is higher than the category 1 datasets. This is a general observation that we would expect that the stronger the noise is, the harder it is to predict the outcomes.

Finally, if we look into the worst-case examples, we see that they are actually performing well in terms of accuracy for the different datasets. The overall conclusion from this analysis is that proposed model is able to learn how to predict the measurement outcomes with high accuracy. The noisy multi-axis datasets had slightly less accuracy than the single-axis and the noiseless datasets, which might be worth investigation and is subject to the future work.

The results of the applications of the trained model are also very promising. The fidelities obtained for the different quantum gates are above 99% including the identity gate, which is equivalent to dynamical decoupling. This indicates that we can use numerical quantum control methods combined with our proposed one. We were also able to show the possibility of estimating the spectrum of the noise using the AS method. These results could be enhanced by including longer pulse sequences, which requires increasing the overall time of evolution. Thus, the proposed framework is general enough to be used for different tasks in quantum control.

In this paper, we presented a machine-learning-based method for characterizing and predicting the dynamics of an open quantum system based on measurable information. Expressing the quantum evolution in terms of the V_O operators instead of a master equation (such as the Lindblad master equation) allows our method to work with general non-Markovian dynamics. We followed a graybox approach that allows us to estimate the V_O operators, which are generally difficult to calculate analytically without assumptions on noise and control signals. We showed the method is applicable to the general case where the noise is defined by a non-unital quantum map, but restricted the numerical experiments in this paper on the case of classical noise (unital dynamics). The numerical results show good performance in terms of prediction accuracy of the measurement outcomes. However, this is not the end of the story. There are lots of points to explore as an extension of this work.

In terms of our control problem, there are two direct extensions. The first relates to that generality of the model used in the whiteboxes. We chose here to study a classical bath because its dynamics was amenable to simulations. However, the learning algorithm itself does not depend on the details of the noise Hamiltonian, and indeed one only needs that Eq. (8) holds—essentially that what we know about about open quantum systems holds—and that given {f_α(t)} one can write U_ctrl(T). A more important direction our results allow, however, is related to the observation that we are characterizing the open quantum system relative to the given set of control capabilities. Here, we chose a simple set to demonstrate how our algorithm learned about the open quantum system dynamics it relative to them (see also ref. ²⁴ for a formal analysis of this observation) and is capable of predicting the dynamics under control functions {f_α(t)} achievable by those capabilities. However, our algorithm is generic, in the sense that it can be applied to a set of control capabilities that is relevant to a specific experimental setup, e.g., when convex sums of Gaussian or Slepian pulses are available or when certain timing constraints must be obeyed, etc. Similar to what we showed here in the sample applications, one can then implement optimal control routines tailored to a specific platform. We are currently working on such targeted result.

On the ML side, the blackboxes can be further optimized to increase the accuracy specially for the noisy multi-axis datasets. There are lots of architectures that one could exploit. We tried to present the problem in a way that that would facilitate for researchers from the machine-learning community to explore and contribute to this field. we emphasize on the importance of understanding the theory so one can know limitations and assumptions of various tools. This is the essence of using the graybox approach, as opposed to using only a blackbox (which is often criticized in the physics community). Moreover, one could make use of existing results in machine-learning that deals with incomplete training data^58,59,60,61. These could be leveraged to reduce the number of required experiments, which would be useful particularly for higher dimensional systems.

In summary, we have established a general ML tool that integrates the concept of a graybox with the problem of characterizing (and eventually controlling) an open quantum system relative to a set of given control capabilities. We made every effort to present the result in a way that is palatable for both the physics and the ML community, with the hopes of establishing a bridge between the two communities. We believe this interaction to be necessary in order to achieve efficient and robust protocols that can tackle the extremely relevant problem of high-quality control of multiple qubits in Noisy Intermediate-Scale Quantum era machines and beyond.