Introduction

Quantum technology promises to deliver exponentially faster computation, provably secure communications, and high-precision sensing1. However, during the fabrication and operation of a quantum device, there are many factors that can significantly impact its functionality, requiring characterization and control techniques to achieve high-level performance. Generally, we are interested in uncovering the unknown relation between the control and the Hamiltonian governing the device, and then utilizing this information to drive the device toward a desired target. Typical targets include unitary gates, a specific Hamiltonian, or certain output probability distributions.

Approaches that directly aim to control the quantum device without first identifying it, includes dynamical decoupling and dynamically corrected gates2,3,4,5, as well as direct gradient-based optimization, such as the commonly used GRAPE algorithm6 and its variants7,8,9,10,11,12,13,14. These techniques only work when the dependence of the Hamiltonian on the control is known, because they are based on optimizing the fidelity to some target with respect to control. In situations where this dependence is unknown, the fidelity (and, in general other cost functions) and/or its gradient, can be computed iteratively from experimental data. The control is optimized after each iteration and directly applied to the system for the next iteration. The physical system becomes part of a feedback architecture for designing the pulses without a need for a model. Examples of this approach are in14,15,16,17, and are sometimes referred to as ‘learning quantum control’18. Evolutionary algorithms, such as Genetic Algorithm (GA) have also been proposed19, as optimization techniques with the advantage of being gradient-free and are more likely to find global minima. These techniques can also be applied with a known model or directly from experimental measurements. Reinforcement learning methods20,21,22,23, are also model-free and have been recently explored for the purposes of removing the reliance on assumptions on the physical system and have been successfully applied to controlling quantum systems.

In many situations, it is important to reconstruct a mathematical model of the system from experimental data, a process referred to as ‘system identification’. An identified model can be used to compare the behavior of a fabricated device to its design, or to understand the underlying noise process affecting the system. As the model can predict the behavior of the system, it can be used for control as well.

The traditional approach to characterizing and controlling physical devices is based on theoretical models of the underlying processes governing the relationship between input and output signals. Example of fitting data to a physical model include24,25. These ‘whitebox’ (WB) models are based on parameter estimation via curve fitting and can be computationally expensive, inaccurate, or incomplete. For example, they do not consider unexpected input parameters or dynamics. Moreover, the models commonly used to describe the dynamics of an open quantum system (such as Lindblad’s master equation), is valid only under strict assumptions and approximations of the noise (such as Markovianity) and the control (such as being ideal impulses). These assumptions do not hold for many quantum platforms, making the use of fixed a priori WB models inaccurate.

To increase accuracy and remove some of the limitations of the WB method, supervised machine learning techniques are proving useful for modeling and controlling complex physical systems. In particular, techniques such as neural networks are, in many cases, superior if not the only viable approach. However, this approach, referred to as ‘blackbox’ (BB), does not provide any information about the underlying physics of the system. Nonetheless, it has been used in many applications such as quantifying Non-Markovianity of quantum systems26, characterizing qubits and environments27,28,29,30, quantum control31,32,33, quantum error correction34,35, optimization of experimental quantum measurements36,37, and calibration of quantum devices38. A closely related approach to system identification is the ‘Hamiltonian Learning’ problem39,40, where a fixed time-independent Hamiltonian (control is fixed) is inferred from quantum measurements.

In situations where the quantities of interest, such as Hamiltonians, unitaries, and noise operators, cannot be directly accessed from the model, the use of a hybrid WB-BB or ‘graybox’ (GB) approach allows for both identify and control of these quantities beyond the measurable dataset. Following the standard control engineering definition41, the aim of GB models is to merge an abstract mathematical structure, such as a neural network, with physical laws. While direct control methods, such as GRAPE, are sometimes referred to as grayboxes, because they are data-driven and may rely on prior knowledge, these methods do not identify a useful mathematical description of the system. The graybox architecture provides access to any physical quantity available from the physical part (WB) of the model.

GB has been proposed to model electrical drift in quantum photonic circuits42, as well as open quantum systems subject to classical43 and quantum noise44, covering the case of a time-dependent Hamiltonian problem. The GB model was also applied in the context of noise detection in the presence of a spectator qubit that acts as a sensor of the environment45, and to geometric quantum gate synthesis46. While GB has been used experimentally to characterize superconducting qubits47, to date, no quantum device has been characterized using a GB model where the identified model was then used to design optimal quantum control.

Here, we experimentally demonstrate how to model and control a quantum device using the GB architecture when the Hamiltonian dependence on the control is unknown. We report high-fidelity preparation of arbitrary unitaries and output probability distributions of a reconfigurable three-mode integrated photonic device and uncover the Hamiltonian dependence on the control. Our GB approach outperforms the traditional model fitting methods and can successfully prepare unitary operations, which are not accessible from the structure of a BB. Our results show a promising approach to enhance quantum control by understanding the physical processes, and open the way to improve the engineering of quantum devices.

Results

Modeling quantum devices

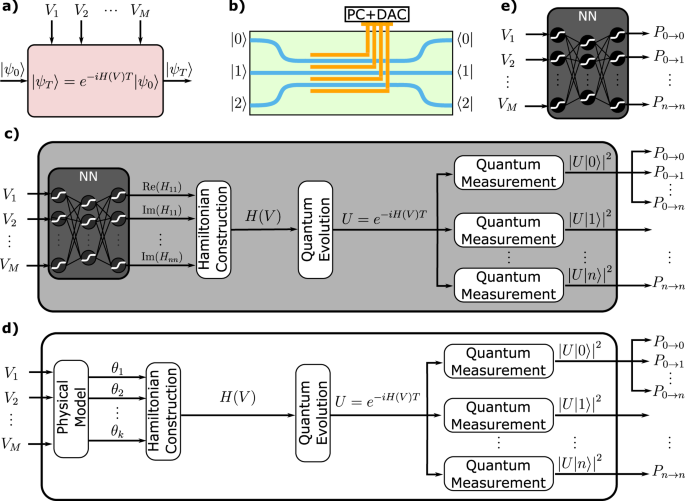
We consider the class of quantum devices, shown in Fig. 1a, described by a time-independent Hamiltonian undergoing a closed-system evolution (i.e., in the absence of quantum noise). Photonic devices are examples of this class when the Hamiltonian is not modulated faster than the evolution time of a propagating photon. We focus on the case where the system is described by a finite N-dimensional Hilbert space (i.e., a qudit). The Hamiltonian governing the dynamics of the system can be represented in the most general form as an N × N complex Hermitian matrix that depends on a set of external controls. We encode the set of controls in a M × 1-dimensional vector \({{{\bf{V}}}}={[{V}_{1},{V}_{2},\cdots {V}_{M}]}^{T}\), where Vk is the kth control. We assume that during the system evolution, the control vector is fixed. An example of such controls is the voltages applied to a reconfigurable photonic chip, schematically shown in Fig. 1b. The system starts in an initial state \(\left\vert {\psi }_{0}\right\rangle\) and evolves to the state \(\left\vert {\psi }_{T}\right\rangle\) at time t = T. The state is then measured on some basis to obtain a set of probability outcomes. A more general form of time-dependent evolution in the presence of unwanted interactions with the environment has been considered in our previous work43.

Fig. 1: Physical and machine learning models of the class of quantum devices considered in this paper.
figure 1

These are described by a time-independent Hamiltonian in the absence of interaction with the environment. a Representation of the class of quantum devices considered in this work. b A schematic of an integrated photonic voltage-controlled reconfigurable waveguide array chip, implementing a noiseless time-independent Hamiltonian. Photons enter from the input port (on the left), undergo a voltage-controlled propagation along the chip, and are then measured at the output port of the chip (on the right). c The structure of the proposed graybox model. The input to the model is the set of M controls, while the outputs are the quantum measurements for the set of computational basis as initial states. Pa→b indicates the transition probability from input port a to output port b. The graybox is a combination of black and white boxes. The blackbox estimates the real and imaginary components of each matrix element of the Hamiltonian. The whitebox layers construct the Hamiltonian matrix and perform the quantum evolution and measurements. d A fully whitebox architecture where a physical model is utilized. The first layer generates predefined Hamiltonian parameters that follow a known analytical dependence. The remaining layers perform the quantum evolution and measurements. e A fully blackbox model where only a generic neural network is utilized with no physical model.

Full size image

Our aim is to obtain an ML model that describes the behavior of the device given a set of controls V and use it for controlling the device. The input to the ML model is the M-dimensional control vector V, while the output is the set of measured outcomes of the state after evolution. Generally, it is required to have informationally-complete measurements to fully characterize a quantum system. Here, we restrict the initial states as well as the measurement basis to the set of computational basis states \(\{\left\vert 0\right\rangle ,\left\vert 1\right\rangle ,\cdots \left\vert N\right\rangle \}\) in order to be compatible with our experimental setup. For each of these N-initial states, we have N possible outcomes with an associated probability Pj→k corresponding to the jth input and kth output, giving a total of N2 outputs. The approach, however, is independent of this choice, and any set of states can be used. In Supplementary Note 4, we discuss a more general measurement scheme. It is important to emphasize that the model input is the set of controls V applied to the system, and not the initial state \(\left\vert {\psi }_{0}\right\rangle\).

Graybox architecture

Our starting point is our theoretical proposal42 for modeling and controlling quantum photonic circuits using a GB architecture. The work aimed at stabilizing the effect of electrical drift and preparing quantum gate sequences at the same time. In order to model such an effect, a GB was desgined to capture variations over a ‘classical’ time scale (i.e. slower than the evolution time of a single photon). So, a recurrent neural network was used, particularly a Gated-Recurrent Unit (GRU) as the black part of the model. The inputs and outputs of the model are slowly time-varying waveforms. However, this resulted in optimal voltage pulses that did not belong to the class of pulses in the training set, which is not available in our experimental device, and may not, in general, be available.

Here, we focus only on modeling the unknown Hamiltonian-voltage dependence, and stabilize the drift in hardware using fast pulsing, a well-known technique in integrated photonics. The pulses have fixed frequency and duty cycle, so the only controllable parameters are the amplitude on each electrode. This makes it possible to restrict the controller solution to the space of training pulses. Therefore, in what follows in this paper, we use standard feed-forward neural networks as opposed to recurrent neural networks, as there is no need to model a sequence over time.

The GB structure we propose, shown in Fig. 1c, consists of a BB (in the form of a neural network) followed by a WB part that processes the outputs of the BB into measurable physical quantities. The purpose of the blackbox is to map the controls V (the model inputs) to the Hamiltonian of the system. The output of the BB then represents the elements of the Hamiltonian matrix. A general N × N complex matrix has 2N2 degree of freedom (N2 components with real and imaginary parts).

Thus, the output layer of the BB must consist of 2N2 neurons. The other BB layers can be designed arbitrarily, and are custom engineered to provide the best performance for a given dataset.

The second layer is a Hamiltonian construction layer that arranges the outputs of the BB into an N × N matrix. A valid Hamiltonian has to be Hermitian (i.e., H† = H) and this is ensured by calculating the Hermitian part of the constructed matrix and discarding the anti-Hermitian part. This can be done simply by adding the matrix to its Hermitian conjugate. The output of this layer is a valid control-dependent Hamiltonian. We did not enforce any structure or constraint on the Hamiltonian, to enable the best fitting allowed by the rules of quantum mechanics for a given dataset.

The Hamiltonian is then followed by subsequent layers that transform the Hamiltonian matrix into the set of probability outcomes–which can be measured experimentally–utilizing the laws of quantum mechanics. Starting from a valid Hamiltonian, there is no need to further use a BB since the dynamical equations are known. This saves the algorithm from trying to learn the rules of quantum mechanics from experimental data, which would complicate the process and result in a less accurate model. We use WB layers for the remaining steps. In particular, there is a layer that calculates the evolution unitary by the matrix exponentiation of the Hamiltonian U = e−iHT, which is the solution of Schrödinger’s time-independent equation. The final part of the GB model is a concatenation of N-layers representing the quantum measurement operation for each of the N input \(\left\vert j\right\rangle\). In each layer we calculate \(\left\vert {\psi }_{T}\right\rangle =U\left\vert j\right\rangle\), where \(\left\vert j\right\rangle\) is the initial state of the system. After evolving the state to \(\left\vert {\psi }_{T}\right\rangle\), the probabilities Pj→k are calculated by taking the absolute value squared of each entry of the state, that is, applying the Born’s rule for quantum expectation values.

The added WB layers do not include any trainable parameter; they only exist in the BB part. Therefore, when we train the model on a dataset, the only updates occur in the BB, generating a set of outputs that can be interpreted as a Hamiltonian.

An important aspect of the GB architecture is that it is independent of the physics of the system, i.e., it provides the most general form of a map between the control vector and the quantum measurements while keeping the most important physical quantities accessible via software, namely Hamiltonian, unitary and evolved state. This is the key aspect needed to perform quantum control as we are usually interested in implementing a quantum gate represented by the unitary or Hamiltonian and not by the measured evolved state. Having access to those quantities, even though the model is trained with quantum measurements, is the key feature of the GB architecture.

Whitebox and blackbox architectures

We benchmark the performance of our GB model against the fully WB and fully BB architectures. The WB approach (Fig. 1d) is equivalent to the standard model (curve) fitting and the details of the architecture depend on the physical system. The assumption is that all the relations between different dynamical variables are exactly known except for the parameters we are fitting. Generally, a WB consists of several layers. The first layer represents the mathematical relations between the controls and the Hamiltonian, with a set of unknown parameters. The input of this layer is the control vector, and the output is a mathematically valid Hamiltonian. The remaining layers are identical to those of the GB and represent quantum evolution and quantum measurements. For some systems, we might need more layers (e.g., to model the fan-in/out in photonic devices48). The WB provides the same access to hidden quantities as the GB and even provides more physics as we know exactly the analytical relations between Hamiltonian and control. However, if we do not know these relations, or they do not match the physical reality, the WB will fail and will not be useful for further applications.

The BB architecture (Fig. 1e) is largely different from the WB model since the relation between the control vector and the quantum measurement is modeled by a neural network. While any structure can be used, in this paper, we consider fully connected neural networks with a softmax output layer of N neurons. This enforces the outputs to form a probability distribution (i.e., positive numbers in [0, 1] whose sum is equal to 1). This is consistent with what the model outputs represent, which are the probability amplitudes of the evolved quantum state. Since we are characterizing with N-initial basis states, we need N of such layers with the initial state chosen accordingly. This will give a total of N2 outputs. The structure of the other hidden layers can only be determined and optimized by examining the performance on an actual dataset. No other physical quantities can be accessed through this architecture, but it is very good in fitting a dataset since it gives the maximum freedom in terms of representation. If we are only interested in controlling the outputs, a BB would be an efficient solution. But, if the goal is to estimate physical quantities (like unitary gates), then a BB model is not useful at all.

Protocol for training, testing, and controlling

Our protocol for training and testing models and controllers is schematically depicted in Fig. 2. It starts with preparing a dataset that will be used to train and test the ML BB. The dataset consists of examples. Each example is made of the M control inputs V and the N2 outputs of the model Pj→k. So we start by generating random values for our control, let the system evolve, then perform the measurements and obtain the probabilities Pj→k. We repeat this for the N input states we consider to obtain all the outputs. The procedure is repeated for multiple examples. The number of examples of the dataset depends on the particular structure of the ML model, the noise level in the experiment, and the acceptable performance level. Generally, the larger dataset is, the better the ML algorithm will perform. In our previous work42, only computer-simulated datasets were considered. In this paper, we create and test experimental datasets. This comes with many challenges including performing the experiment itself, the limited dataset size (to be feasible to collect), and the presence of noise not modeled by the quantum dynamics. In particular, initially, we found that statistical noise caused inconsistencies in the dataset, resulting in a poor performance of the method. As a result, we modified the dataset collection protocol, in particular the normalization of output power measurements as discussed in Supplementary Note 3. This extra step improved the performance of the ML significantly.

Fig. 2: Protocol schematic.
figure 2

The first step is to construct an experimental dataset by applying controls to the system and measuring the corresponding outputs. The dataset is then used to train the machine learning models (1). Next, the trained models are tested (2) for generalization by comparing their output predictions against a different experimental testing dataset. After that, the trained models can be used to optimize controls (3) to achieve a certain target, which could be a Hamiltonian, a unitary gate, or an output probability distribution. Finally, the obtained controls are tested (4) experimentally and the controlled system output is compared against the desired target.

Full size image

After the dataset is collected, it is split into the training and testing subsets, and the ML model is trained. The purpose of training is to minimize a loss function that measures the distance between the predictions and actual outputs from the training dataset. In42, the loss function measured the similarity between waveforms, because the model was modeling drift, and the RMSprop algorithm49 was used for the training. Here, we use the standard mean square error (MSE) as a loss function and use the ADAM algorithm50 for training. Once the model is trained, its parameters are fixed and do not change in any of the remaining protocol stages. Next, the model is evaluated using the testing dataset, and its predictions are compared to the true corresponding values. The testing examples are not included in the optimization procedure, so they provide an unbiased evaluation of the performance of the model.

Let’s now consider the trained model for control purposes. In this case, the model acts as a replacement for the actual experimental setup and can be probed via software for any purpose. In42, the controller was designed to be a GRU, and therefore the optimal control was not restricted to any class of pulses. Here, we use a different controller that is designed to directly obtain the parameters of a fixed pulse shape (i.e. the voltage amplitudes). We consider two types of applications. The first is for obtaining the values of the control V to achieve a target output (i.e., probability amplitudes). In this case, we use the MSE as the control cost function, and the optimal control vector V* can be expressed as

$${{{{\bf{V}}}}}^{* }=\mathop{\arg \min }\limits_{{{{\bf{V}}}}\in {{{\mathcal{I}}}}}{({\hat{{{{\bf{y}}}}}}_{P}({{{\bf{V}}}})-{{{{\bf{y}}}}}_{d})}^{T}({\hat{{{{\bf{y}}}}}}_{P}({{{\bf{V}}}})-{{{{\bf{y}}}}}_{d})$$
(1)

where \({\hat{{{{\bf{y}}}}}}_{P}(\cdot )\) is the ML output predictions, yd is the desired target, and \({{{\mathcal{I}}}}\) is the control domain, which reflects the maximum allowed range for the controls. To get accurate results, the ML model should be trained with dataset examples that lie in the same control domain as well. Note that the internal ML model parameters that define \({\hat{{{{\bf{y}}}}}}_{P}(\cdot )\) are not allowed to change during the optimization as they have been fixed after the training.

The other case is for achieving a target quantum gate (i.e., a target unitary). For this application, we use the gate fidelity as the control cost function for the controller defined as

$$F(U,W)=\frac{{\left\vert {{{\rm{tr}}}}({U}^{{\dagger} }W)\right\vert }^{2}}{{N}^{2}},$$
(2)

where U and W are two unitary matrices, and N is their dimension. The gate fidelity lies in the range [0, 1], with 1 representing the maximum overlap between the two gates. The optimal control voltages can then be represented as

$${{{{\bf{V}}}}}^{* }=\mathop{\arg \max }\limits_{{{{\bf{V}}}}\in {{{\mathcal{I}}}}}F({\hat{y}}_{U}({{{\bf{V}}}}),{U}_{d})$$
(3)

where \({\hat{y}}_{U}(\cdot )\) is the evolution unitary obtained from the ML model, and Ud is the desired target gate. In this case, we can only use the GB and WB models, since a BB does not provide access to unitaries as discussed earlier. With this modular approach, the optimization algorithm of the controller can be chosen arbitrarily. While we choose a gradient-based method in this paper, other techniques such as genetic algorithms could also be used.

Finally, the optimal controls for a set of targets are applied experimentally, and the system is measured to construct the ‘control’ dataset. This dataset is then assessed and compared against the desired targets. Our main goal is to control a quantum system, and thus the assessment of any model should not just rely on its prediction capabilities, but also on how it performs in conjunction with a controller when tested experimentally.

Experimental results

We tailor the design of the models described above around the device used for the experimental verification for our proposal, a voltage-controlled quantum photonic circuit of continuously coupled waveguides based on lithium niobate technology, and schematically shown in Fig. 1b. The details about the chip’s fabrication and its physical model are given in Supplementary Notes 1 and 2. The chip has 3 waveguides, corresponding to a qutrit system, and is controlled by 4 electrodes and their respective voltages. In principle, there is no or negligible cross-talk in our device. This is guaranteed by the confinement of the electric field within the material due to the shielding effect from neighboring electrodes, as opposed to other technologies such as thermo-optic switching51. Thus, the electrodes can be activated simultaneously, which is how we perform the experiments in this paper. We implemented the ML models using the TensorFlow Python package52,53, applied the protocol for training the three models, and then verified the performance of the controllers. The details of the implementations are also given in Supplementary Note 3. Moreover, we provide independent results of applying our method to a simulated synthetic dataset in Supplementary Note 4 including a showcase for a 32-mode chip with 33 electrodes.

The results of the models training and testing as well as the control performance, are reported in Table 1. The MSE evaluated at each iteration for training and testing sets are shown in Fig. 3a, b.

Table 1 Comparison of the performance of each model on the training, testing, and control experimental datasets, as well as the experimental fidelities (average and instances greater than 99%) for 1000 randomly prepared output distributions and unitary gates.
Full size table
Fig. 3: Experimental performance of the machine learning models.
figure 3

The whitebox model consists of fan-in, reconfigurable, and fan-out sections, each modeled as a real-valued tri-diagonal Hamiltonian in addition to a linear dependence on voltage for the reconfigurable section. a Results of training the different models on the experimental dataset. The MSE is plotted versus iteration number. b The results of evaluating the different models on the testing set.

Full size image

Discussion

The plot of the learning curve in Fig. 3a shows the superior performance of the GB in terms of accuracy compared to the WB. This is due to the constraints imposed by the physical model that is used to construct the Hamiltonian in the case of the WB. As detailed in Supplementary Note 2, the commonly used device Hamiltonian is assumed to be tri-diagonal, real-valued, and linearly dependent on voltages. Our results show that these assumptions do not hold for a real device, and thus the degradation of the WB performance. On the other hand, the GB learns a general mathematically valid Hamiltonian and thus is able to better fit the experimental data. Initially, we designed the GB to enforce the Hamiltonian to be real-valued but otherwise arbitrary, and the fitting was not good. When we relaxed this assumption to allow a complex-valued Hamiltonian, the results were improved. Here we note that the Hamiltonian remains Hermitian to allow a unitary evolution, and thus it does not model losses. The normalization procedure (detailed in Supplementary Note 3) that we perform on the power measurements makes it unnecessary to model losses. The BB had a similar performance to GB, with the main drawback of losing the physical picture. In terms of the testing performance, Fig. 3b shows that the three models do not overfit, as the final MSE of the testing set is close to the final MSE of the training set. This means that the models do not memorize the examples of the training set. In other words, the model generalizes–there’s no significant loss in prediction accuracy–confirming that the dataset, the model structure, and the training algorithm are well designed. Furthermore, the GB and BB clearly perform better than the WB.

The performance of the models is limited by the size of the dataset. Because the experimental data always suffer from some level of noise, the minimum MSE obtainable without overfitting is limited as well. Usually, the acceptable level of MSE depends on the specific application. In this paper, our application is to control the chip to obtain target power distributions as well as target unitary operations. The ML models then act as a replacement/simulator of the actual setup. The experimental assessment of the optimal control will determine whether the model performance is accepted or needs improvement. In general, the way to improve models is by constructing very large datasets, which is the standard approach in most typical ML applications. For engineering applications, where we characterize and control a physical device, we are limited by how many measurements we can obtain. Thus, it becomes a tradeoff between the amount of time and resources needed to construct the dataset experimentally and the accuracy of the trained models, which will also affect the performance of the controller.

The histogram of the controller fidelities between the desired target and the experimental measurements for 1000 randomly prepared output power distributions and 1000 randomly prepared unitary gates are shown in Fig. 4a, b, respectively. The plots show that the WB is particularly skewed towards lower fidelities (minimum is 80.53% compared to a minimum of approximately 91% for GB and BB for the output controller). Similarly, for the gate controller, the minimum fidelity is 86.6% and 94.95% for WB and GB. In Fig. 4c, we summarize the statistics of the MSE between the ML model predictions and actual outputs for the training and testing datasets, in comparison with the MSE between the experimentally controlled measurements and the targets for each of the two controllers.

Fig. 4: Experimental quantum control performance.
figure 4

The distribution of the fidelity between the experimentally measured output power distribution and the desired target distribution for the three models. The whitebox model utilizes a real-valued tri-diagonal Hamiltonian with linear dependence on voltages, in addition to fan-in and fan-out sections. The results are for a the output controller, and b the unitary controller. The reported values are the average over the three distributions corresponding to each possible initial state. c Violin plot showing the statistics of the MSE obtained for the training, testing, and control datasets. The error bars depicted as the horizontal lines represent from bottom to top, the minimum, median, and maximum, respectively. The plot also shows an estimated kernel density for the data.

Full size image

The results of the controller for obtaining a target power distribution show once again the superior performance of the GB and BB over the WB in terms of both MSE and average fidelity. The same controller/optimization algorithm and cost function are used for the three models. Thus, the lower performance comes from the lower accuracy of the WB model itself. When considering the controller for target unitary, it is only possible to use a WB or a GB as they are the only models that can give access to the overall unitary evolution matrix. A BB cannot be utilized in this case since it only encodes the dynamics in an abstract machine-suitable format, and does not provide any physical picture.

The performance assessment of ML-based algorithms on real rather than synthetic datasets is critical. Different noise sources could affect the data in unpredicted ways, which may also be difficult to simulate. This can affect the performance of the ML algorithm. We see that the final MSE of training and testing for the experimental dataset is two orders of magnitude less than that of the synthetic dataset (shown in Supplementary Note 4). However, the control performance on the experimental dataset is accepted and thus, we also accept the model prediction performance. In other situations, this might not be the case, and the ML design has to be modified to achieve higher performance. Therefore, using a design based on simulations such as ref. 42 and applying it directly to an experimental dataset would not result in adequate performance, and so the whole workflow needs to be re-executed.

Determining the required dataset size, as well as NN architecture and complexity for higher-dimensional systems, is generally difficult and has to be studied case by case. In Supplementary Note 4, we show promising results for a simulated 32-mode chip. And while the dataset and neural network sizes had to be increased, the overall protocol was still feasible to execute.

Finally, the GB provides sufficient physical insights for most purposes, for example, in Fig. 5a, b, where the tunability of the Hamiltonian as a function of a single electrode voltage is explored. The figure shows the GB prediction of the different Hamiltonian elements as a function of the voltage applied to a single electrode. We can use these predictions more generally when more than one electrode is tuned (although it would be more difficult to plot in this situation) for unitary control. We can use the GB to predict the unitary given the set of voltages even though the dataset originally did not include this information but rather the power distribution. Another advantage of using the GB, compared to WB, is the incorporation of unmodelled effects such as cross-talk. While the effect is negligible in our technology, in other situations, it can be difficult to have an exact/accurate WB model.

Fig. 5: Dependence of the Hamiltonian elements on a subset of input voltages, as predicted by the graybox model.
figure 5

a Real and b imaginary parts of the Hamiltonian matrix elements as a function of voltage when all electrodes are grounded except the first electrode. It should be noted that the imaginary parts of H11, H22, and H33 are by definition equal to zero. The non-linear dependence, the second off-diagonal elements, and the imaginary components indicate an effective Hamiltonian being estimated for a time-dependent system, attributed to the non-homogeneity of the chip along the propagation direction.

Full size image

It is also important to realize that this predicted Hamiltonian, besides not being unique mathematically, represents physically an effective quantity, and so it will differ in structure (such as the existence of an imaginary part) from the ideal Hamiltonian that one may expect for a system. Depending on the purpose of the use of the GB we can control how much we make it ‘blacker’ or ‘whiter’. For control applications, the best architecture is to have this effective Hamiltonian. In another application, such as modeling a device for the purpose of completely understanding the physics, the architecture of the GB might need to be modified to allow Hamiltonians that are closer to some expected structure. In Supplementary Note 5, we explore this idea in more detail. In particular, we explore the relaxation of the WB assumptions gradually until we reach the structure of the GB. The results show that the best architecture that fits the experimental data is a complex non-tri-diagonal Hamiltonian with non-linear dependence on the control voltage. This suggests that the reconfigurable section of the chip has variations along the propagation direction, which could be the result of fabrication imperfections. In other words, the estimated Hamiltonian effectively represents a time-dependent system. Finally, it is worth mentioning that reaching this conclusion was based on interpreting the mathematical structure obtained from the GB. Thus, the GB approach helped us understand better the behavior of our system.

In summary, we have shown how a GB model can be designed for a general quantum device, trained on experimental data, and verified by generating target unitary operations and output distributions with high fidelity. The performance was benchmarked against WB and BB models, showing the superior performance of our approach. Our approach is general and can be applied to any quantum system, it can be extended to time-dependent and open quantum systems with the need to modify the ML structure and dedicated dataset-taking process for specific hardware or quantum systems43,44,45. There are many possible extensions to this work as well. One possibility is to design a GB for other physical models, such as a Lindblad master equation for Markovian open quantum systems. One could also consider a hybrid approach between Hamiltonian learning using Genetic Algorithms (such as ref. 54,55) and our numerical GB for the purpose of obtaining more detailed physical models. In terms of the ML aspects of this application, a study about the scaling requirements for the NN structures of the GB in relation to the dimensionality of the system would be interesting. However, it will be challenging because asymptotic analysis of ML algorithms is difficult or might be impossible. On the other hand, relying on numerical analysis might not be sufficient since the analysis will be restricted to a particular range of the scaling parameter and cannot be generalized outside that range. Another aspect related to any ML algorithm is the requirements of the training dataset size. For complex devices, it can be challenging to collect a large-sized dataset. However, some emerging techniques can facilitate this process, including incremental learning56, transfer learning57, and adaptive online learning58. While these techniques are constantly developing in classical ML literature, there is still a gap in porting such methods to physics-based applications, especially quantum applications.