Abstract
Quantum data are susceptible to decoherence induced by the environment and to errors in the hardware processing it. A future fault-tolerant quantum computer will use quantum error correction to actively protect against both. In the smallest error correction codes, the information in one logical qubit is encoded in a two-dimensional subspace of a larger Hilbert space of multiple physical qubits. For each code, a set of non-demolition multi-qubit measurements, termed stabilizers, can discretize and signal physical qubit errors without collapsing the encoded information. Here using a five-qubit superconducting processor, we realize the two parity measurements comprising the stabilizers of the three-qubit repetition code protecting one logical qubit from physical bit-flip errors. While increased physical qubit coherence times and shorter quantum error correction blocks are required to actively safeguard the quantum information, this demonstration is a critical step towards larger codes based on multiple parity measurements.
Similar content being viewed by others
Introduction
A recent roadmap1 for fault-tolerant quantum computing marks a transition from storing quantum data in physical qubits to protection of logical qubits by quantum error correction (QEC)2,3,4,5,6 as the fourth of the seven development stages. Experimental demonstrations of QEC to date, using nuclear magnetic resonance7, trapped ions8,9, photons10, superconducting qubits11 and nitrogen–vacancy centres in diamond12,13, have circumvented stabilizers at the cost of decoding at the end of a QEC cycle. This decoding leaves the quantum information vulnerable to physical qubit errors until re-encoding, violating a basic requirement for fault tolerance. Following steady improvements in qubit coherence, coherent control and measurement over 15 years, superconducting quantum circuits are well poised to face this outstanding challenge common to all quantum computing platforms. Initial experiments using superconducting processors include one round of either bit-flip or phase-flip QEC with decoding11, and the stabilization of one Bell state using dissipation engineering14. Independent, parallel work15 demonstrates the detection of general errors on a single Bell state using stabilizer measurements.
By analogy to the classical repetition code that maps bit 0 (1) to 000 (111), the quantum version maps the one-qubit superposition state α|0〉+β|1〉 to the entangled Greenberger–Horne–Zeilinger-type (GHZ) state α|0t0m0b〉+β|1t1m1b〉 of three data qubits (labelled top, middle and bottom)16. The stabilizers of this code consist of two-qubit parity measurements described by Hermitian operators ZtZm and ZmZb. While GHZ-type states are eigenstates of both stabilizers with eigenvalue +1, their corruption by a bit-flip error on one data qubit produces eigenstates with a unique pattern of −1 eigenvalues. Measuring stabilizers can thus discretize and signal single bit-flip errors without affecting the encoded information (that is, the probability amplitudes α and β). Depending on the error signalled, the logical qubit is transformed to an orthogonal two-dimensional subspace. It is both sufficient and better to keep track of this subspace transformation rather than attempt to return to the original subspace using correcting π pulses, which are not perfect and thus introduce errors.
In this work, we construct these stabilizers as parallelized indirect measurements using ancillary qubits, and evidence their non-demolition character by generating three-qubit entanglement from the superposition states. We demonstrate stabilizer-based QEC on the minimal unit of encoded quantum information, a logical qubit, restricting to bit-flip errors.
Results
Stabilizer measurements in a superconducting processor
This realization of bit-flip QEC with stabilizer measurements employs a superconducting quantum processor with 12 quantum elements (Fig. 1a) exploiting resonant and dispersive regimes of circuit quantum electrodynamics17. Three data transmon qubits (Dt, Dm and Db) encode the logical qubit. Two ancillary transmons (At and Ab), two bus resonators (Bt and Bb) and two dedicated ancilla readout resonators are used for the stabilizer measurements. Dedicated readout resonators on data qubits are used to quantify performance (fidelity measures, entanglement witnessing and state tomography). All readout resonators couple to one feedline used for all qubit control and readout pulses. The feedline output couples to a single amplification chain allowing readout of all qubits by frequency-division multiplexing18. Ancilla readout fidelity is boosted by a Josephson parametric amplifier19 with a bandwidth covering both ancilla readout frequencies (9 MHz apart).
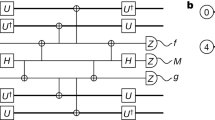
(a) Photograph of the processor (scale bar on the bottom-right indicates 1 mm) showing the position and interconnections of data qubits (Dt, Dm and Db), ancilla qubits (At and Ab), buses (Bt and Bb) and dedicated readout resonators. These resonators couple to one common feedline to which all readout and microwave control pulses are applied18. Flux-bias lines (ports 2–5 and 7) allow control of the qubit transition frequencies on nanosecond timescale (Supplementary Fig. 1). Details of the processor, including fabrication, parameters and performance benchmarks are provided in Methods and Supplementary Table 1. (b) Block diagram for characterizing bit-flip QEC by parallelized parity measurements of pairs (Dt, Dm) and (Dm, Db). The Dm state  is first encoded into the logical qubit state
is first encoded into the logical qubit state  . Coherent or incoherent bit-flip errors are then introduced on data qubits with independent single-bit-flip probability perr. Parallelized ZtZm and ZmZb stabilizer measurements discretize these errors and the two-bit measurement result PtPb is interpreted as signalling either no error or error on one qubit. (c) Gate sequence implementing the stabilizer measurements by parallelized interaction with ancilla qubits and projective ancilla measurements. Each ancilla is prepared in a superposition state that is transferred to the respective bus with an iSWAP gate (diagonal lines). Consecutive CPHASE gates between each bus and the coupled data qubits (vertical lines) encode the data-qubit parity in the quantum phase of the bus superposition state. The final iSWAP transfers this state to the ancilla, and the latter is then projectively measured in the |±〉 basis. Halfway through the interaction step, a refocusing π pulse is applied to Dm to reduce inhomogeneous dephasing.
. Coherent or incoherent bit-flip errors are then introduced on data qubits with independent single-bit-flip probability perr. Parallelized ZtZm and ZmZb stabilizer measurements discretize these errors and the two-bit measurement result PtPb is interpreted as signalling either no error or error on one qubit. (c) Gate sequence implementing the stabilizer measurements by parallelized interaction with ancilla qubits and projective ancilla measurements. Each ancilla is prepared in a superposition state that is transferred to the respective bus with an iSWAP gate (diagonal lines). Consecutive CPHASE gates between each bus and the coupled data qubits (vertical lines) encode the data-qubit parity in the quantum phase of the bus superposition state. The final iSWAP transfers this state to the ancilla, and the latter is then projectively measured in the |±〉 basis. Halfway through the interaction step, a refocusing π pulse is applied to Dm to reduce inhomogeneous dephasing.
Building on recent developments20,21, we construct quantum non-demolition stabilizer measurements in a two-step process combining entanglement with ancilla qubits and their projective measurement. Measuring the stabilizer ZtZm involves an iSWAP gate between At and Bt, two CPHASE gates between Bt and each of Dt and Dm, and a final iSWAP transferring the Bt state onto At. These interactions correlate the joint states of Dt and Dm with even/odd (e/o) number of excitations with orthogonal states of At. Subsequently, At is measured by interrogating its dispersively coupled resonator. Conveniently, the interaction and measurement steps needed for both the stabilizers can be partially parallelized (Fig. 1c). (Note that a refocusing π pulse is applied to Dm after its interactions to minimize its inhomogeneous dephasing.)
We begin characterizing these stabilizer measurements by testing their ability to detect the parities of the computational states |itjmkb〉, i,j,k∈{0,1}. Because all of these states are eigenstates of ZtZm and ZmZb, a fixed two-bit measurement outcome PtPb∈{ee,eo,oe,oo} is expected for each one. Histograms of declared double parities clearly reveal the correlation (Fig. 2). The average assignment fidelity of 71%, defined as the probability of correct double-parity assignment averaged over the eight states, is limited by errors in the interaction step. An upper bound of 91% is set by the combined readout error for the two ancilla measurements (Supplementary Table 1).
Single-shot histograms for top (a) and bottom (b) ancilla readout signals Vt and Vb at the end of the sequence implementing the parallelized stabilizer measurements, with data-qubit computational states as input. The chosen thresholds for discretization of Vt and Vb (dashed vertical lines) maximize the parity assignment fidelities. (c) Double-parity assignment probabilities for each computational state input. The dashed horizontal line at 0.91 marks the loss of average assignment fidelity exclusively from ancilla readout errors.
Two- and three-qubit entanglement by stabilizer measurements
The next test probes the ability of each stabilizer to discern two-qubit parity subspaces while preserving coherence within each. Specifically, we target the generation of two- and three-qubit entanglement (2QE and 3QE) via single and double stabilizer measurements on a maximal superposition state. The gate sequence in Fig. 1c is executed with Dt and Db both prepared in  and Dm in
and Dm in  . First, we activate one stabilizer by performing the initial π/2 rotation only on the corresponding ancilla, and measure the data-qubit-pair witness operators
. First, we activate one stabilizer by performing the initial π/2 rotation only on the corresponding ancilla, and measure the data-qubit-pair witness operators  ,
,  (ref. 22) based on fidelity to even- and odd-parity Bell states, respectively. Each of these operators witnesses 2QE whenever the expectation value
(ref. 22) based on fidelity to even- and odd-parity Bell states, respectively. Each of these operators witnesses 2QE whenever the expectation value  . With postselection on result o, either one of
. With postselection on result o, either one of  or
or  witnesses 2QE at almost all values of
witnesses 2QE at almost all values of  (Fig. 3a,b). A dual result is obtained with postselection on e, for which
(Fig. 3a,b). A dual result is obtained with postselection on e, for which  witness entanglement (data not shown). Note that in both cases the parity of the generated entanglement differs from the detected one due to the refocusing π pulse on Dm.
witness entanglement (data not shown). Note that in both cases the parity of the generated entanglement differs from the detected one due to the refocusing π pulse on Dm.
Starting with the data qubits in the state  , we selectively perform stabilizer measurements by activating the corresponding ancilla, i.e., preparing it in a maximal superposition state. (a,b), Performing one parity measurement generates entanglement between the paired data qubits. Measured average
, we selectively perform stabilizer measurements by activating the corresponding ancilla, i.e., preparing it in a maximal superposition state. (a,b), Performing one parity measurement generates entanglement between the paired data qubits. Measured average  of the four witness operators
of the four witness operators  and
and  involving the data qubits paired by activating the top (a) or bottom (b) ancilla only and postselection on Pt=o and Pb=o, respectively. Entanglement is witnessed whenever
involving the data qubits paired by activating the top (a) or bottom (b) ancilla only and postselection on Pt=o and Pb=o, respectively. Entanglement is witnessed whenever  (shaded area). The weak oscillations in
(shaded area). The weak oscillations in  result from false positives, which we have partially reduced here by postselecting more strongly than the threshold maximizing the average parity assignment fidelity. Standard deviations of
result from false positives, which we have partially reduced here by postselecting more strongly than the threshold maximizing the average parity assignment fidelity. Standard deviations of  (∼0.007, smaller than the symbol size) are estimated by bootstrapping 31. (c), Measured average of the Mermin operator
(∼0.007, smaller than the symbol size) are estimated by bootstrapping 31. (c), Measured average of the Mermin operator  with both ancillas activated and data strongly postselected on PtPb=oo (black circles). Three-qubit entanglement is witnessed whenever
with both ancillas activated and data strongly postselected on PtPb=oo (black circles). Three-qubit entanglement is witnessed whenever  (shaded area). A stronger violation of the Mermin inequality is observed when targeting the GHZ state
(shaded area). A stronger violation of the Mermin inequality is observed when targeting the GHZ state  using unitary gates only (white circles). The average standard deviations of 0.1 (encoding by measurement) and 0.08 (encoding by gates) are smaller than the symbol size. (d), Tomography (absolute value of the density matrix elements) of the
using unitary gates only (white circles). The average standard deviations of 0.1 (encoding by measurement) and 0.08 (encoding by gates) are smaller than the symbol size. (d), Tomography (absolute value of the density matrix elements) of the  -maximizing state generated by double-parity measurement. The fidelity F=〈GHZ|ρ|GHZ〉 is 73%. For comparison, targeting this state with gates achieves F=82%.
-maximizing state generated by double-parity measurement. The fidelity F=〈GHZ|ρ|GHZ〉 is 73%. For comparison, targeting this state with gates achieves F=82%.
We continue building multi-qubit entanglement by activating both parity measurements and postselecting on the two-bit result (Fig. 3c,d, and Supplementary Fig. 2). Ideally, PtPb=oo collapses the maximal superposition onto the GHZ-type state  . Genuine 3QE is witnessed whenever
. Genuine 3QE is witnessed whenever  , where
, where  is the Mermin operator XtXmXb−YtYmXb−YtXmYb−XtYmYb (ref. 23). With postselection on PtPb=oo,
is the Mermin operator XtXmXb−YtYmXb−YtXmYb−XtYmYb (ref. 23). With postselection on PtPb=oo,  versus
versus  reaches 2.5 (best fit, Fig. 3c). Full state tomography at the optimal
reaches 2.5 (best fit, Fig. 3c). Full state tomography at the optimal  reveals a fidelity 〈GHZ(0)|ρ|GHZ(0)〉=73% to the ideal GHZ state (Fig. 3d).
reveals a fidelity 〈GHZ(0)|ρ|GHZ(0)〉=73% to the ideal GHZ state (Fig. 3d).
This 3QE-by-measurement protocol can also be used to perform the encoding step of bit-flip QEC. Ideally, the state |+t〉 (α|0m〉+β|1m〉) |+b〉 is mapped onto α|1t1m1b〉+β|0t0m0b〉 up to the transformation XtXb, Xt, Xb, I signalled by PtPb=ee, eo, oe, oo, respectively (the amplitudes α and β, in addition to the parities, are also exchanged by the refocusing π pulse on Dm). Postselection on PtPb=oo (Supplementary Fig. 3) encodes with 73% fidelity, averaged over the six cardinal input states of Dm,  ). For comparison, implementing the standard unitary encoding11,24,25 using our gate toolbox (Supplementary Fig. 4) achieves 82% average fidelity.
). For comparison, implementing the standard unitary encoding11,24,25 using our gate toolbox (Supplementary Fig. 4) achieves 82% average fidelity.
QEC of bit-flip errors
Finally, we use this encoding by gates to demonstrate bit-flip QEC by parallelized stabilizer measurements (Fig. 4a). Bit-flip errors are coherently added via X rotations by an angle θ, yielding a single-qubit bit-flip probability perr=sin2(θ/2) (adding incoherent errors at this stage yields very similar results, see Methods and Supplementary Fig. 5). While the three-bit code is by design only resilient to errors on a single qubit, we also consider the realistic case where such error can occur with the same probability on any of the three qubits. Therefore, we consider two scenarios: the errors added on only one data qubit and the errors added independently on all the three. In both scenarios, we assume no prior knowledge of error probability and literally interpret the stabilizer measurement results as though they were perfect. We first quantify QEC performance using the average fidelity F3Q to the ideal three-qubit state accounting for the subspace transformation  signalled by PtPb=ee,eo,oe,oo (in order):
signalled by PtPb=ee,eo,oe,oo (in order):
(a) Sequence used to assess performance of bit-flip QEC. After encoding by gates, either coherent (θ∈[0,π]) or incoherent (θ=0 or π) errors are introduced with single-qubit bit-flip probability perr. Next, parallelized stabilizer measurements are either performed or replaced by an equivalent idling period. Partial tomography at this point is used to obtain the three-qubit fidelity F3Q and the logical fidelity FL. The calculation of FL assumes incoherent second-round errors with the same perr and a perfect decoding (dashed boxes). (b) Three-qubit fidelity F3Q as a function of perr with and without QEC under two scenarios: coherent errors applied on Dm (squares) and on all data qubits (circles). Standard deviations (0.005 for squares, 0.004 for circles) estimated by bootstrapping are smaller than the symbol size. The dashed line indicates the fidelity ceiling imposed by encoding errors. (c) FL as function of perr, obtained from the same data as in b. The average standard deviation of 0.005 is smaller than the symbol size. The individual contributions of the six cardinal states  to F3Q and FL are shown in Supplementary Fig. 7. (d) FL for all combinations of one and zero incoherent errors on all data qubits before and after QEC or idling. Error combinations are labelled m/n, with m (n) the number of errors before (after) QEC or idling. The case 1/1 is divided in two: errors on the same data qubit (1/1a) or on different qubits (1/1b).
to F3Q and FL are shown in Supplementary Fig. 7. (d) FL for all combinations of one and zero incoherent errors on all data qubits before and after QEC or idling. Error combinations are labelled m/n, with m (n) the number of errors before (after) QEC or idling. The case 1/1 is divided in two: errors on the same data qubit (1/1a) or on different qubits (1/1b).

Here,  is the ideal encoded cardinal state, ppq is the measured probability of PtPb=pq, and ρ(j,pq) is the experimental pq-conditioned density matrix. The near constancy of F3Q(perr) with errors on one qubit and the second-order dependence with errors on all three qubits (Fig. 4b) reflect the ability of the stabilizers to discretize and signal single-qubit bit-flip errors without decoding.
is the ideal encoded cardinal state, ppq is the measured probability of PtPb=pq, and ρ(j,pq) is the experimental pq-conditioned density matrix. The near constancy of F3Q(perr) with errors on one qubit and the second-order dependence with errors on all three qubits (Fig. 4b) reflect the ability of the stabilizers to discretize and signal single-qubit bit-flip errors without decoding.
To assess the ability of QEC to detect added errors without unfairly penalizing for intrinsic decoherence and encoding errors, we compare F3Q with the stabilizer interactions replaced by idling for equal duration (with a refocusing Dm pulse):

Without QEC, one expects a linear decrease in F3Q with errors on one qubit as one bit flip orthogonally transforms the encoded state. The slight curvature observed reflects residual coherent errors in encoding. The non-monotonicity of F3Q with errors on all qubits reflects that triple errors perform a logical bit flip, which leaves |+L〉 and |−L〉 unchanged. Comparing the curves suggests that QEC provides net gains for perr≳15% in the first case and for perr≳10% in the second (Fig. 4b).
Discussion
However, the true merit of QEC hinges on the ability to suppress the accumulation of errors. We believe that a better comparison is the logical state fidelity FL following two rounds of errors with QEC or idling in between. FL is defined as the fidelity to the initial unencoded Dm state following an ideal decoder  (Fig. 4a) that is resilient to a bit-flip error remaining in any one qubit. For example, with QEC and a second-round error
(Fig. 4a) that is resilient to a bit-flip error remaining in any one qubit. For example, with QEC and a second-round error  ,
,

Here we consider the scenario with errors on all three qubits and only incoherent second-round errors. We expect QEC to win over idling in select cases, such as single errors on both rounds but on different qubits, all of which we observe (Fig. 4d and also Supplementary Fig. 6). Weighing in all the possible cases (from 0 to 3 errors in each round) according to their probability, we find that the current fidelity of the stabilizer measurements precludes boosting FL for the cardinal states using this quantum repetition code at any perr (Fig. 4c). This stricter comparison sets the benchmark for gauging future improvements in QEC.
In summary, we have realized parallel stabilizer measurements with ancillary qubits and used them to perform a quantum repetition code on a superconducting circuit. Stabilizer-based QEC can detect bit-flip errors on data qubits while maintaining the encoding at the logical level, thus meeting a necessary condition for fault-tolerant quantum computing. Evidently, it remains a priority to extend qubit coherence times and shorten the QEC step to boost logical fidelity. In the longer term, parallelized ancilla-based parity measurements as demonstrated here may be used to protect a logical qubit against general errors with a Steane6,26 or small surface code27.
Methods
Processor fabrication
The integrated circuit is fabricated on a c-plane sapphire substrate. A NbTiN film (80 nm) is reactively sputtered at 3 mTorr in a 5% N2 in Ar atmosphere, resulting in a superconducting critical temperature of 15.5 K and normal-state resistivity of 110 μΩcm. This film is e-beam patterned using SAL601 resist and etched by SF6/O2 RIE to define all coplanar waveguide structures: feedline, resonators and flux-bias lines. The transmon Josephson junctions and shunting interdigitated capacitors are patterned using PMGI/PMMA e-beam lithographed resist and double-angle shadow evaporation of Al with intermediate oxidization. Air bridges are added to suppress slot-line propagation modes, to connect ground planes and to allow the crossing of transmission lines (Supplementary Fig. 8). Bridge fabrication starts with a 6-μm-thick PMGI layer, which is patterned and then reflowed at 220 °C for 5 min, producing a gently arched profile. A second MAA/PMMA resist layer is spun and e-beam patterned to define the bridge geometry. Finally, Ti (5 nm) and Al (450 nm) are e-beam evaporated. The 2 mm by 7 mm chip is diced and cleaned in 88 °C NMP for 30 min.
Experimental setup
The quantum processor is anchored to the mixing chamber plate of a dilution refrigerator with 15–20 mK base temperature. A detailed schematic of the experimental setup at all temperature stages is shown in Supplementary Fig. 8. The single coaxial line for readout and microwave control has in-line attenuators and absorptive low-pass filters providing thermalization, noise reduction and infrared radiation shielding. Coaxial lines for flux control are broadband attenuated and bandwidth limited (1 GHz) with reactive and absorptive low-pass filters.
Qubit control
Most microwave pulses for X and Y qubit rotations have a Gaussian envelope in the main quadrature (5 ns sigma and 20 ns total duration), and a derivative-of-Gaussian envelope in the other (DRAG pulses28). Wah–Wah pulses29 combining DRAG with sideband modulation are used for Dt and Ab to avoid leakage in Dm and Db, respectively. Taking advantage of the proximity in frequency between Dt and At, and between Dm and Ab, we coherently control the five qubits by sideband modulation of three carriers (Supplementary Fig. 8).
Flux pulses for iSWAPs are sudden (12 ns duration), while those for CPHASEs are mostly fast adiabatic30 (40 ns). The pulse for CPHASE between Dm and Bt is kept sudden (19 ns) to avoid leakage during the crossing of Dm through Bb. Pulse distortion resulting from the flux control bandwidth is minimized by manual optimization of convolution kernels.
Qubit readout
The five qubits are readout by frequency division multiplexing18. The readout pulses for data and ancilla qubits are separately generated by sideband modulation of the two carriers.
The amplitude and duration of readout pulses are chosen to maximize assignment fidelity. Dt, Dm and Db readout pulses have 1,200, 1,000 and 700 ns duration, respectively. The signal-to-noise boost provided by the Josephson parametric amplifier allows shorter ancilla qubit readouts, 600 ns (550 ns) for At (Ab). The amplified feedline output is split and downconverted with two local oscillators. The two signals are amplified, digitized, demodulated and integrated to yield one voltage for each qubit measured. The low crosstalk between the qubit readouts is evidenced by simultaneous measurement immediately following preparation of the 32 combinations of the five qubits in either |0〉 or |1〉 (Supplementary Fig. 9).
Using the method of ref. 20 based on Hahn echo sequences, we have bound the dephasing of each data qubit induced by the ancilla measurements to <1% (data not shown). Since data-qubit fidelity loss during ancilla measurements is dominated by intrinsic decoherence and our main interest is to quantify the ability of stabilizers to detect the intentionally added errors, we have opted to advance the data qubit measurements, making them simultaneous to those of ancillas (Supplementary Fig. 4).
Initialization
The four qubits {Dt, Db, At and Ab} and two buses {Bt and Bb} are initialized to their ground state by postselection on six measurements performed before any encoding or manipulation protocol. The buses are initialized by swapping states with their coupled ancilla immediately after initialization of the latter. Dm is initialized by swapping its excitation (∼10%) with that of Bb (∼1%). The postselected fraction of runs (50–60%) have a residual excitation of 1–2% in every quantum element.
Gate sequence
Gates are parallelized as much as possible. We note two important exceptions. Because of frequency crowding and the common feedline, pulses targeting one qubit induce ac Stark shifts on untargeted qubits. We serialize single-qubit control to restrict the effect of these shifts to residual phase rotations on unaddressed qubits. Also, the first iSWAP between Bt and At and CPHASE between Bt and Dm (Fig. 1c) are applied before populating Bb to avoid a strong dispersive shift of Dm. All others iSWAPS, CPHASE gates and ancilla measurements are simultaneous.
Incoherent errors
We have also tested stabilizer-based QEC with incoherent first-round errors generated using π rotations (Supplementary Fig. 5). Following encoding of a Dm cardinal input state  , we apply the eight combinations of error/no error on the three data qubits. We calculate F3Q and FL for each combination and weigh by the corresponding probability.
, we apply the eight combinations of error/no error on the three data qubits. We calculate F3Q and FL for each combination and weigh by the corresponding probability.
Additional information
How to cite this article: Ristè, D. et al. Detecting bit-flip errors in a logical qubit using stabilizer measurements. Nat. Commun. 6:6983 doi: 10.1038/ncomms7983 (2015).
References
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496 (1995).
Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098–1105 (1996).
Bennett, C. H., DiVincenzo, D. P., Smolin, J. A. & Wootters, W. K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824–3851 (1996).
Laflamme, R., Miquel, C., Paz, J. P. & Zurek, W. H. Perfect quantum error correcting code. Phys. Rev. Lett. 77, 198–201 (1996).
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).
Cory, D. G. et al. Experimental quantum error correction. Phys. Rev. Lett. 81, 2152–2155 (1998).
Chiaverini, J. et al. Realization of quantum error correction. Nature 432, 602–605 (2004).
Schindler, P. et al. Experimental repetitive quantum error correction. Science 332, 1059–1061 (2011).
Pittman, T. B., Jacobs, B. C. & Franson, J. D. Demonstration of quantum error correction using linear optics. Phys. Rev. A 71, 052332 (2005).
Reed, M. D. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382–385 (2012).
Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014).
Taminiau, T. H., Cramer, J., van der Sar, T., Dobrovitski, V. V. & Hanson, R. Universal control and error correction in multi-qubit spin registers in diamond. Nature Nanotech 9, 171–176 (2014).
Shankar, S. et al. Autonomously stabilized entanglement between two superconducting quantum bits. Nature 504, 419–422 (2013).
Córcoles, A. D. et al. Detecting arbitrary quantum errors via stabilizer measurements on a sublattice of the surface code. arXiv:quant-ph/1410.6419 (2014).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information Cambridge Univ. Press (2000).
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Jerger, M. et al. Frequency division multiplexing readout and simultaneous manipulation of an array of flux qubits. Appl. Phys. Lett. 101, 042604 (2012).
Castellanos-Beltran, M. A., Irwin, K. D., Hilton, G. C., Vale, L. R. & Lehnert, K. W. Amplification and squeezing of quantum noise with a tunable Josephson metamaterial. Nat. Phys. 4, 929–931 (2008).
Saira, O.-P. et al. Entanglement genesis by ancilla-based parity measurement in 2D circuit QED. Phys. Rev. Lett. 112, 070502 (2014).
Chow, J. M. et al. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nat. Commun. 5, 4015 (2014).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Mermin, N. D. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 65, 1838–1840 (1990).
DiCarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010).
Neeley, M. et al. Generation of three-qubit entangled states using superconducting phase qubits. Nature 467, 570–573 (2010).
Nigg, D. et al. Quantum computations on a topologically encoded qubit. Science 345, 302–305 (2014).
Tomita, Y. & Svore, K. M. Low-distance surface codes under realistic quantum noise. Phys. Rev. A 90, 062320 (2014).
Motzoi, F., Gambetta, J. M., Rebentrost, P. & Wilhelm, F. K. Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 103, 110501 (2009).
Vesterinen, V., Saira, O.-P., Bruno, A. & DiCarlo, L. Mitigating information leakage in a crowded spectrum of weakly anharmonic qubits. arXiv:cond-mat/1405.0450 (2014).
Martinis, J. M. & Geller, M. R. Fast adiabatic qubit gates using only σ z control. Phys. Rev. A 90, 022307 (2014).
Efron, B. Bootstrap methods: another look at the jacknife. Ann. Statist. 7, 1–26 (1979).
Acknowledgements
We thank K.W. Lehnert for providing the parametric amplifier, D.J. Thoen and T.M. Klapwijk for sputtering of NbTiN films, K.M. Svore, T.H. Taminiau, D.P. DiVincenzo, E. Magesan and J.M. Gambetta for fruitful discussions, and N.K. Langford, G. de Lange, L.M.K. Vandersypen and R. Hanson for helpful comments on the manuscript. We acknowledge the funding from the Netherlands Organization for Scientific Research (NWO), the Dutch Organization for Fundamental Research on Matter (FOM) and the EU FP7 project ScaleQIT.
Author information
Authors and Affiliations
Contributions
A.B. fabricated the processor, with design input from O.-P.S. and L.D.C. O.-P.S. and V.V. performed the initial tune-up. D.R., M.-Z.H. and S.P. performed measurements and data analysis. S.P., D.R. and L.D.C. prepared the manuscript with feedback from all the other authors. L.D.C. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-9 and Supplementary Table 1 (PDF 22064 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ristè, D., Poletto, S., Huang, MZ. et al. Detecting bit-flip errors in a logical qubit using stabilizer measurements. Nat Commun 6, 6983 (2015). https://doi.org/10.1038/ncomms7983
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7983
This article is cited by
-
Overcoming leakage in quantum error correction
Nature Physics (2023)
-
Factorization by quantum annealing using superconducting flux qubits implementing a multiplier Hamiltonian
Scientific Reports (2022)
-
Logical-qubit operations in an error-detecting surface code
Nature Physics (2022)
-
Performance of superconducting quantum computing chips under different architecture designs
Quantum Information Processing (2022)
-
Experimental QND measurements of complementarity on two-qubit states with IonQ and IBM Q quantum computers
Quantum Information Processing (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.