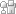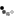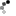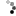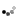« Prev Next »
A central question in biology is whether observed variation in a particular trait is due to environmental or to biological factors, sometimes popularly expressed as the "nature versus nurture" debate. Heritability is a concept that summarizes how much of the variation in a trait is due to variation in genetic factors. Often, this term is used in reference to the resemblance between parents and their offspring. In this context, high heritability implies a strong resemblance between parents and offspring with regard to a specific trait, while low heritability implies a low level of resemblance.
Quantifying Heritability
Phenotypes that vary between the individuals in a population do so because of both environmental factors and the genes that influence traits, as well as various interactions between genes and environmental factors. Unless they are genetically identical (e.g., monozygotic twins in humans, inbred lines in experimental populations, or clones), the individuals in a population tend to vary in the genotypes they have at the loci affecting particular traits. The combined effect of all loci, including possible allelic interactions within loci (dominance) and between loci (epistasis), is the genotypic value. This value creates genetic variation in a population when it varies between individuals. In fact, heritability is formally defined as the proportion of phenotypic variation (VP) that is due to variation in genetic values (VG).
Genotypes or genotypic values are not passed on from parents to progeny; rather, it is the alleles at the loci that influence the traits that are passed on. Therefore, to predict the average genotypic value of progeny and their predicted average phenotype, investigators need to know the effect of alleles in the population rather than the effect of a genotype. The effect of a particular allele on a trait depends on the allele's frequency in the population and the effect of each genotype that includes the allele. This is sometimes termed the average effect of an allele. The additive genetic value of an individual, called the breeding value, is the sum of the average effects of all the alleles the individual carries (Falconer & Mackay, 1996). According to the principles of Mendelian segregation, one allele from each locus is present in each gamete, and in this way, additive genetic values are passed on from parents to progeny. Indeed, because each offspring receives a different set of alleles from its parents, half of the additive genetic variance in the population occurs within families.
Broad-sense heritability, defined as H2 = VG/VP, captures the proportion of phenotypic variation due to genetic values that may include effects due to dominance and epistasis. On the other hand, narrow-sense heritability, h2 = VA/VP, captures only that proportion of genetic variation that is due to additive genetic values (VA). For definitions and decomposition of components of variation, you can read more about phenotypic variance. Note that often, no distinction is made between broad- and narrow-sense heritability; however, narrow-sense h2 is most important in animal and plant selection programs, because response to artificial (and natural) selection depends on additive genetic variance. Moreover, resemblance between relatives is mostly driven by additive genetic variance (Hill et al., 2008).
Given its definition as a ratio of variance components, the value of heritability always lies between 0 and 1. For instance, for height in humans, narrow-sense heritability is approximately 0.8 (Macgregor et al., 2006). For traits associated with fitness in natural populations, heritability is typically 0.1–0.2 (Visscher et al., 2008).
Heritability Estimation
In Figure 1, examples are given of a scatterplot of progeny phenotypes (y-axis) and the average of two parental phenotypes (x-axis), for traits with high (0.9) and low (0.1) heritability. The straight line is the best-fit linear relationship between y and x, obtained from a statistical technique called linear regression. The slope of the regression line is an estimate of narrow-sense heritability. For the high heritability of 0.9 (Figure 1b), there still is a lot of variation around the regression line, because the correlation between offspring phenotype and mid-parent value is √(½)h2, which is only 0.64 for h2 = 0.9. Even when the heritability is 1.0 (i.e., there is no environmental variation), the phenotypes of offspring and parents are not identical because of random segregation of alleles from parents to progeny. This explains, for example, why human siblings can vary considerably in height, despite the heritability of height being very large.
When phenotypic measures are available on individuals with a mixture of relationships, both within and across multiple generations, or when the design is unbalanced (e.g., there are unequal numbers of observations per family), estimates of additive genetic variance and environmental components are most efficiently calculated via statistical methods that use all data simultaneously and take account of the exact properties of the data. Such methods are iterative and computationally more intensive than estimates of heritability that are based upon regression or correlation coefficients.
Estimating Heritability: Caveats
When estimating heritability from the observed and expected resemblance between relatives, a model is necessary to specify the expected resemblance in terms of genetic and environmental factors. Sometimes this model is straightforward; for example, it may posit that the observed resemblance between half-sibling dairy cows on different farms is due solely to additive genetic factors inherited from the common parent. In other cases, a model's assumptions may be open to questioning. For example, in human twin analysis, it is usually assumed that the resemblance between monozygotic and dizygotic twin pairs due to shared environment is the same.
Recently, new methods that exploit the use of genetic marker data have been proposed and applied to estimate heritability essentially free of such assumptions regarding the nature of between-family variation (Visscher et al., 2006). These methods are based upon the correlation between phenotypic and genetic similarity within families. They exploit the fact that there is variation in identity (defined here as the proportion of the genome that is shared identical-by-descent) between pairs of individuals that have the same expected value and that this variation can be measured with genetic markers. Variation in identity arises because of the random segregation of chromosomes during meiosis. For full siblings in humans, the mean identity is 50%, with a standard deviation of approximately 4%. Hence, some full siblings share only 40% of their genome by descent, while others share 60%. If those siblings who share more of their genome than average are phenotypically more similar to each other than those siblings who share less than average, then this similarity is most likely due to genetic factors. This assumption was the basis of a study by Visscher et al. (2006), who estimated a narrow-sense heritability of height in humans of 0.8 using pairs of full siblings, without making any assumption about the variation between families.
Heritability Is Not Necessarily Constant
Interestingly, heritabilities are not constant. For example, estimates of heritability for first lactation milk yield in dairy cattle nearly doubled from approximately 25% in the 1970s to roughly 40% in recent times. Heritability can change over time because the variance in genetic values can change, the variation due to environmental factors can change, or the correlation between genes and environment can change. Genetic variance can change if allele frequencies change (e.g., due to selection or inbreeding), if new variants come into the population (e.g., by migration or mutation), or if existing variants only contribute to genetic variance following a change in genetic background or the environment. The same trait measured over an individual's lifetime may have different genetic and environmental effects influencing it, such that the variances become a function of age. For example, variance in weight at birth is influenced by maternal uterine environment, and variance in weight at weaning depends on maternal milk production, but variance of mature adult weight is unlikely to be influenced by maternal factors, which themselves have both a genetic and environmental component. Heritabilities may be manipulated by changing the variance contributed by the environment. Empirical evidence for morphometric traits suggests lower heritabilities in poorer environments, but not for traits more closely related to fitness (Charmantier & Garant, 2005). Understanding how heritability changes with environmental stressors is important for understanding evolutionary forces in natural populations (Charmantier & Garant, 2005).
Misconceptions of the Heritability Concept
There are a number of common misconceptions on the exact meaning and interpretation of heritability (Visscher et. al., 2008). Heritability is not the proportion of a phenotype that is genetic, but rather the proportion of phenotypic variance that is due to genetic factors. Heritability is a population parameter and, therefore, it depends on population-specific factors, such as allele frequencies, the effects of gene variants, and variation due to environmental factors. It does not necessarily predict the value of heritability in other populations (or other species). Nevertheless, it is surprising how constant heritabilities are across populations and species (Visscher et. al., 2008).
Applications of heritability estimation are broad and cross a range of disciplines, from evolutionary biology to agriculture to human medicine. In humans, estimation of heritability has been applied to diseases and behavioral phenotypes (e.g., IQ), and it has helped establish that a substantial proportion of variation in risk for many disorders, like schizophrenia, autism, and attention deficit/hyperactivity disorder, is genetic in origin.
References and Recommended Reading
Charmantier, A., & Garant, D. Environmental quality and evolutionary potential: Lessons from wild populations. Proceedings of the Royal Society, Biological Sciences 272, 1415–1425 (2005)
Falconer, D. S., & Mackay, T. F. C. Introduction to Quantitative Genetics (Harlow, UK, Longman, 1996)
Hill, W. G., et al. Data and theory point to mainly additive genetic variance for complex traits. PLoS Genetics 4, e1000008 (2008)
Macgregor, S., et al. Bias, precision and heritability of self-reported and clinically measured height in Australian twins. Human Genetics 120, 571–580 (2006)
Visscher, P. M., et al. Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. Public Library of Science Genetics 2, e41 (2006)
———. Heritability in the genomics era—Concepts and misconceptions. Nature Reviews Genetics 9, 255–266 (2008) (link to article)



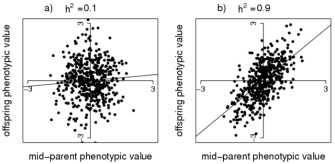
 Figure 1: Heritability estimation.
Figure 1: Heritability estimation.