« Prev Next »
Sampling Basics
Why we sample.
How many samples?
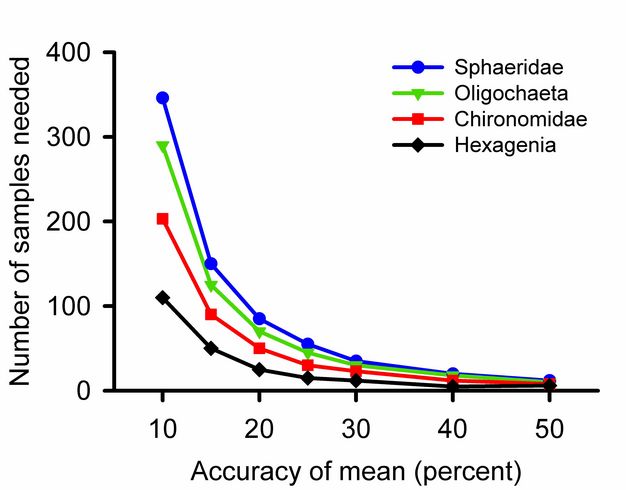
For most parameters a single sample provides an unbiased guess at the average. The first measured length of a nail, height of a person, or abundance of birds may be higher, lower, or equal to the true parameter. Adding samples increases the accuracy of a calculated average. Three is the minimum number of samples required for most statistical tests, but will not detect small differences among groups. Excellent community ecology has been done with five replicates per treatment or fewer. If one can take more replicates, however, the effort will reveal more subtle differences.
Keep individual samples separate.
Diversity Sampling
Samples underestimate community-wide richness.
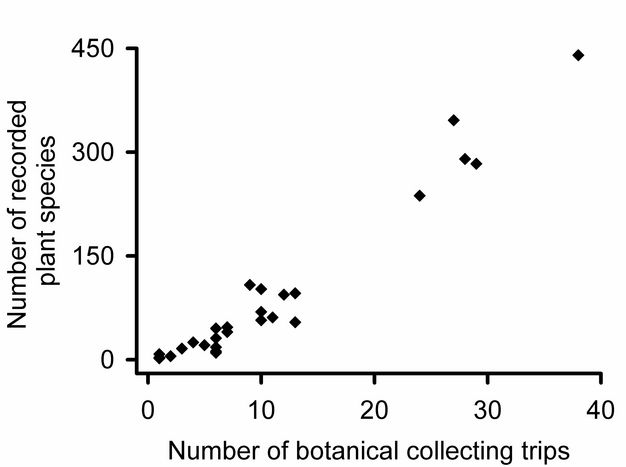
How many community samples?
Sample-based comparisons.
What to record.
|
Species |
Burned |
Control |
|
American beech |
1 | 0 |
|
Black cherry |
7 | 0 |
| Black oak | 0 | 1 |
|
Grey birch |
11 | 0 |
|
Pitch pine |
3 | 22 |
| Red maple | 0 | 35 |
| Red oak | 14 | 0 |
|
Service berry |
2 | 3 |
|
White oak |
0 | 3 |
|
White pine |
12 | 1 |
| Table 1. Numbers of trees greater than 1.4 m tall recorded by Saint Michael’s College students in 20 x 20 m quadrats in Camp Johnson in Colchester Vermont in September 2007. The ‘Burned’ treatment had been subjected to a controlled burn in 1998 and the ‘Control’ represents an adjacent fire-suppressed area. | ||
What are we measuring?
Which community is more diverse?
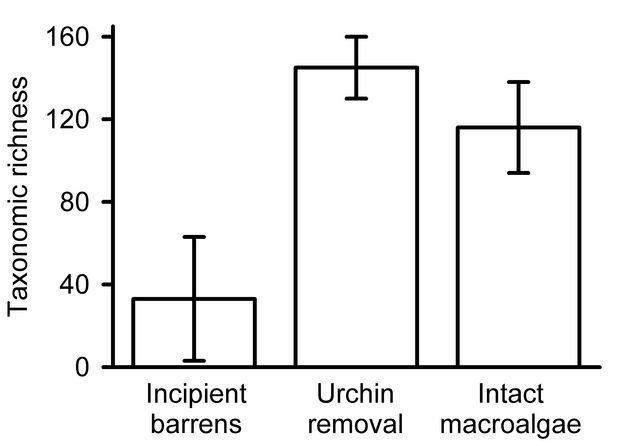
Estimating and presenting overall diversity.
Confounded by abundance?
Removing abundance effects: Rarefaction.
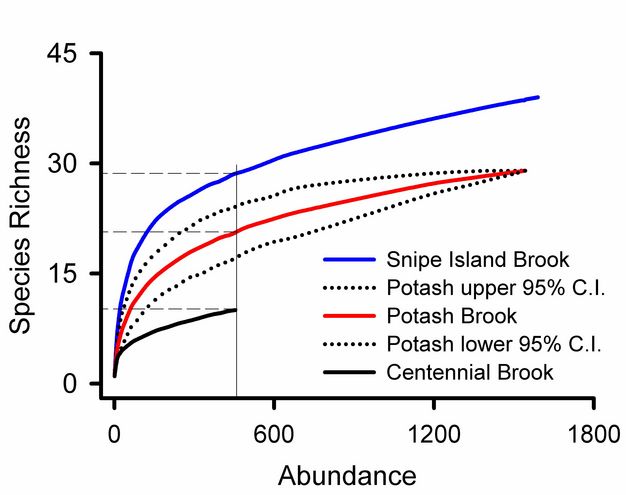
Because diversity reflects richness and evenness, a number of other measurement and presentation approaches have been devised. Each approach has advantages that can reveal useful and interesting data patterns.
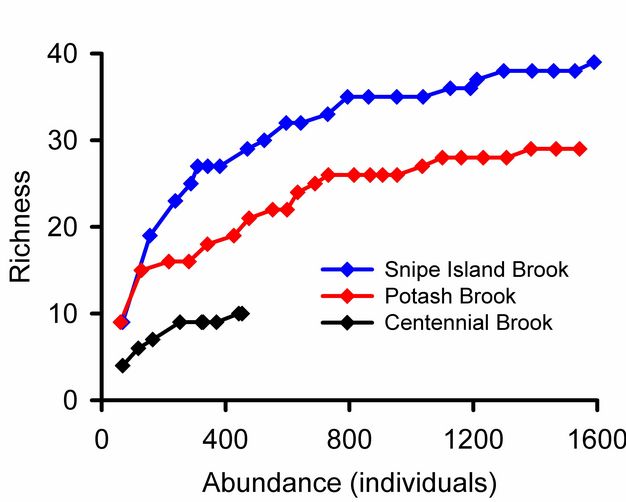
Collector’s curves.
Collector’s curves rise rapidly when the relative abundances of the species are even (Gotelli & Coleman 2001). A sample from a community dominated by one species may contain only that dominant species and we might sample many individuals before observing more species. A collector’s curve would remain horizontal before very gradually stepping up as we record rare species. In even communities, early samples add more species and the graph steps up rapidly before leveling off when most species are accumulated. Unlike rarefaction curves that start at abundance = 1, richness = 1, collector's curves start at the abundance and richness of the first sample. Differences in shape between collector's curves and rarefaction curves reflect patchiness or non-randomness in the distributions of organisms in samples (Gotelli & Coleman 2001).
Rare species contribute uncertainty to all estimates of overall diversity. A collector’s curve illustrates this problem (Figure 5): it would be tempting to consider that the plateau in the Snipe Island Brook collector’s curve at 35 families represented a reasonably complete inventory of the groups present. Adding three more samples did not add a single new taxon. But the 17th sample added a new group, and three additional families were added by subsequent samples. The families added by later samples were rare groups missed by earlier samples and represented by just one or two individuals. The frequency of rare species relative to abundant species is used to assess confidence in overall estimates of taxonomic richness (Chao 1987). Lack of visual representation of the frequency of rare species is a weakness of collector’s curves addressed by log-normal plots illustrated below.
Log-normal plots.
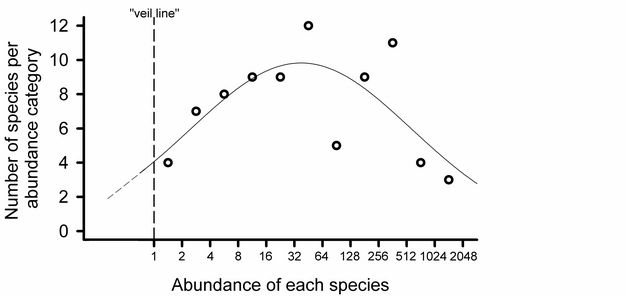
Preston’s (1948; Figure 6) analogy of a "veil line" described the discovery of rarer species by increasing the sampling effort. Early samples reveal the common species, while rare species remain hidden behind the imaginary veil line. Additional sampling shifts the veil line to the left. Thus, as rarer species are sampled and increases in abundance are recorded for each of the species already observed, the entire distribution is shifted to the right.
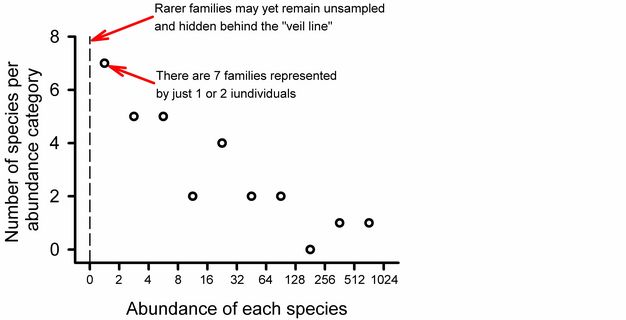
Using Preston’s (1948) approach we can see that uncertainty in our estimate of overall richness at Potash Brook is well justified (Figure 7). Seven families are represented by only one or two individuals: this is the largest category on the graph, suggesting that we can look forward to many additional days of sampling in Vermont to improve our estimate of taxonomic diversity (it could be worse). Additional sampling effort will increase the abundance of most species in our samples and probably yield previously unseen taxa.
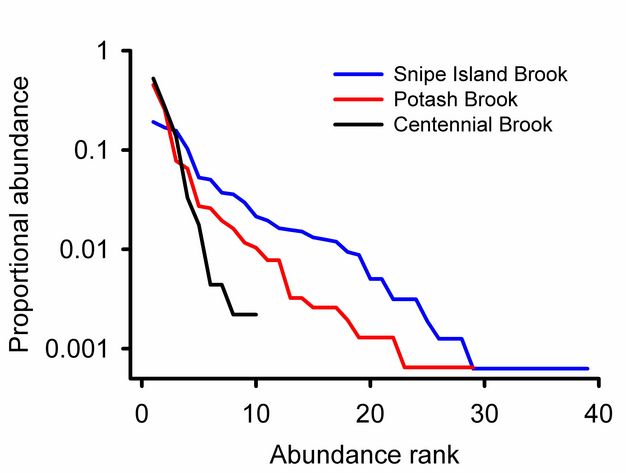
Rank abundance curves.
Rank abundance curves for Vermont streams (Figure 8) show that Snipe Island Brook has more families than Centennial Brook and that the relative abundances of those species are more evenly distributed. We can also see that 0.52 of the individuals from Potash Brook are from a single taxon. The most abundant family in Snipe Island Brook represents 0.19 of the community.
Summary
References and Recommended Reading
Colwell, R. K. & Coddington, J. A. Estimating terrestrial biodiversity through extrapolation. Philosophical Transactions of the Royal Society B: Biological Sciences 345, 101–118 (1994).
Connor, E. F. & Simberloff, D. Species number and compositional similarity of the Galapagos flora and avifauna. Ecological Monographs 48, 219–248 (1978).
Eckblad, J. W. How many samples should be taken? Bioscience 41, 346–348 (1991).
Gotelli, N. J. & Colwell, R. K. Quantifying biodiversity: Procedures and pitfalls in the measurement and comparison of species richness. Ecology Letters 4, 379–391 (2001).
Gotelli, N. J. & Ellison, A. M. A Primer of Ecological Statistics. Sunderland, MA: Sinauer & Associates, 2004.
Gotelli, N. J. & Entsminger, G. L. Ecosim: Null models software for ecology. Version 7.0. Jericho, VT: Acquired Intelligence Inc. & Kesey-Bear, 2009. (link)
Ling, S. Range expansion of a habitat-modifying species leads to loss of taxonomic diversity: A new and impoverished reef state. Oecologia 156, 883–894 (2004).
Magurran, A. E. Ecological Diversity and its Measurement. Princeton, NJ: Princeton University Press, 1988.
Preston, F. W. The commonness, and rarity, of species. Ecology 29, 254–283 (1948).
Pyron, M. Characterizing communities. Nature Education Knowledge 1, 20 (2010).
Simberloff, D. Properties of the rarefaction diversity measurement. The American Naturalist 106, 414–418 (1972).