Abstract
Enzyme turnover numbers (kcat) are key to understanding cellular metabolism, proteome allocation and physiological diversity, but experimentally measured kcat data are sparse and noisy. Here we provide a deep learning approach (DLKcat) for high-throughput kcat prediction for metabolic enzymes from any organism merely from substrate structures and protein sequences. DLKcat can capture kcat changes for mutated enzymes and identify amino acid residues with a strong impact on kcat values. We applied this approach to predict genome-scale kcat values for more than 300 yeast species. Additionally, we designed a Bayesian pipeline to parameterize enzyme-constrained genome-scale metabolic models from predicted kcat values. The resulting models outperformed the corresponding original enzyme-constrained genome-scale metabolic models from previous pipelines in predicting phenotypes and proteomes, and enabled us to explain phenotypic differences. DLKcat and the enzyme-constrained genome-scale metabolic model construction pipeline are valuable tools to uncover global trends of enzyme kinetics and physiological diversity, and to further elucidate cellular metabolism on a large scale.

Similar content being viewed by others
Main
The enzyme turnover number (kcat), which defines the maximum chemical conversion rate of a reaction, is a critical parameter for understanding the metabolism, proteome allocation, growth and physiology of a certain organism1,2,3. There are large collections of kcat values available in the enzyme databases BRENDA4 and SABIO-RK5, which are, however, still sparse compared to the variety of existing organisms and metabolic enzymes, largely due to the lack of high-throughput methods for kcat measurement. Additionally, experimentally measured kcat values have considerable variability due to varying assay conditions such as pH, cofactor availability and experimental methods6. Altogether, the sparse collection and considerable noise limit the use of kcat data for global analysis and may mask enzyme evolution trends.
In particular, enzyme-constrained genome-scale metabolic models (ecGEMs), where the whole-cell metabolic network is constrained by enzyme catalytic capacities and thereby able to accurately simulate the maximum growth abilities, metabolic shifts and proteome allocations, rely heavily on genome-scale kcat values2,7. Over the past decade, ecGEMs (or models following the concept of enzyme constraints) have been separately developed for several well-studied organisms7 including Escherichia coli8,9, Saccharomyces cerevisiae2,10, Chinese hamster ovary cells11 and Homo sapiens12. Due to the limitations of kcat measurements13 and the reliance on enzyme commission (EC) number annotations to search for kcat values in those developed pipelines2,8,10, the reconstruction of ecGEMs for lesser-studied organisms or large-scale reconstruction for multiple organisms has remained a challenge7,14. Moreover, even for those well-studied organisms, the kcat coverage is far from complete13,15,16. In a S. cerevisiae ecGEM, only 5% of all enzymatic reactions have fully matched kcat values in BRENDA2. When data are missing, previous ecGEM reconstruction pipelines typically assume kcat values from similar substrates, reactions or other organisms, which can result in model predictions deviating from experimental observations7. There is a clear requirement for obtaining large-scale kcat values to improve model accuracy and yield more reliable phenotype simulations17.
Deep learning has been applied and shown great performance in modelling chemical spaces18, gene expression19, enzyme-related parameters such as enzyme affinity20 and EC numbers21. Previously, Heckmann and colleagues employed machine learning approaches to predict E. coli kcat values based on features such as average metabolic fluxes and catalytic sites obtained from protein structures16. However, such features are typically hard to obtain, which allows the application of this approach only to the most well-studied organisms such as E. coli.
To this end, we developed a deep learning approach (DLKcat) that uses substrate structures and protein sequences as inputs, and demonstrated its capability for the large-scale prediction of kcat values for various organisms, as well as for identifying key amino acid residues that affect these predictions. We showcased the predictive power of the deep learning model by predicting genome-scale kcat profiles for 343 yeast/fungi species, accounting for more than 300,000 enzymes and 3,000 substrates. The predicted kcat profiles enabled reconstruction of 343 ecGEMs for the yeast/fungi species through an automatic Bayesian-based pipeline, which can accurately simulate growth phenotypes among yeast species and identify the phenotype-related key enzymes.
Results
Construction of a deep learning approach for k cat prediction
The deep learning approach DLKcat was developed by combining a graph neural network (GNN) for substrates and a convolutional neural network (CNN) for proteins (Fig. 1). Substrates were represented as molecular graphs converted from the simplified molecular-input line-entry system (SMILES), and protein sequences were split into overlapping n-gram amino acids (the string of contiguous sequences consisting of n items). We generated a comprehensive dataset from the BRENDA4 and SABIO-RK5 databases to train the neural network. Incomplete database entries with missing information and redundant entries were filtered out to ensure a dataset of unique entries with substrate name, substrate SMILES information, EC number, protein sequence, organism name and kcat value. The final dataset contained 16,838 unique entries catalysed by 7,822 unique protein sequences from 851 organisms and converting 2,672 unique substrates (Supplementary Figs. 1 and 2). This dataset was randomly split into training, validation and test datasets by 80%, 10% and 10%, respectively, while five times of random splitting indicated the robustness of the deep learning model (Supplementary Fig. 3).
a, DLKcat, the approach developed for kcat prediction by combining a GNN for substrates and a CNN for proteins. b, Information extraction from GEMs as the input for the deep learning model to predict kcat values. c, The developed Bayesian facilitated pipeline to reconstruct ecGEMs using the predicted kcat profiles from the deep learning model.
Deep learning model performance for k cat prediction
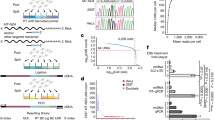
The effects of hyperparameters on deep learning performance were evaluated by learning curves (Supplementary Fig. 4). With the selected optimal parameters (r-radius substrate subgraphs, in which r is the number of hops from a vertex of substrate structure, 2; n-gram amino acids, 3; vector dimensionality, 20; time steps in GNN, 3; number of layers in CNN, 3), the deep learning model was trained. The root mean square error (r.m.s.e.) of kcat predictions gradually decreased with increasing epoch (Fig. 2a), where one epoch is one iteration of the dataset passing through the neural network. A final deep learning model trained and stored for further use had a r.m.s.e. of 1.06 for the test dataset, signifying that predicted and measured kcat values were overall within one order of magnitude (Fig. 2a). A high predictive accuracy could be observed on both the whole dataset (training, validation and test datasets) (Fig. 2b; Pearson’s r = 0.88) and the test dataset (Supplementary Fig. 5a; Pearson’s r = 0.71; Supplementary Fig. 5b for test dataset where at least either the substrate or enzyme was not present in the training dataset; Pearson’s r = 0.70). The predicted kcat values were categorized according to the metabolic context of the enzymes (Supplementary Table 1), and enzymes involved in primary central and energy metabolism yielded significantly higher kcat values than enzymes involved in intermediary and secondary metabolism (Supplementary Fig. 5c), in agreement with previous observations6.
a, The r.m.s.e. of kcat prediction during the training process. b, Performance of the final deep learning model. The correlation between predicted kcat values and those present in the whole dataset (training, validation and test datasets) was evaluated. The brightness of colour represents the density of data points. Student’s t-test was used to calculate the P value for Pearson’s correlation. c, Enzyme promiscuity analysis on the whole dataset. For enzymes with multiple substrates, we divided the substrates into preferred and alternative by their experimentally measured kcat value, and then used the predicted kcat values for this box plot. Random substrates were randomly chosen from the compound dataset in our training data, except for the documented substrates and products for the tested enzyme. We evaluated 945 promiscuous enzymes in the whole dataset (n = 945 for preferred substrates, n = 4,238 for alternative substrates, n = 945 for random substrates). d, Comparison of the predicted kcat values for the native substrates and the underground substrates with the human aldo–keto reductase enzyme as a case study. Here, we defined those substrates with the top 10% catalytic ability (experimental kcat value) as the native substrates (n = 6), while those with the last 10% catalytic ability (experimental kcat value) were considered as the underground substrates as defined in the reference (n = 6)24. In each box plot (c and d), the central band represents the median value, the box represents the upper and lower quartiles and the whiskers extend up to 1.5 times the interquartile range beyond the box range. A two-sided Wilcoxon rank sum test was used to calculate the P values in c and d.
The deep learning model was able to show enzyme promiscuity. Understanding enzyme promiscuity and the related underground metabolism is a key topic in evolutionary biology22,23. DLKcat-predicted kcat values (Fig. 2c) were higher for preferred substrates (median kcat = 11.07 s–1) compared to alternative substrates (median kcat = 6.01 s–1; P = 1.3 × 10–12) and random substrates (median kcat = 3.51 s–1; P = 9.3 × 10–6) for promiscuous enzymes in the whole dataset, while the same trend was identified in the test dataset (Supplementary Fig. 5d; P < 0.05). The concept of native and underground metabolism24 could be exemplified with the rich experimental kcat data that are available for human aldo–keto reductase and 61 substrates, where DLKcat could differentiate (Fig. 2d; P = 0.0039) between native (top 10% experimental kcat values, median = 2.22 s–1) and underground (last 10%, median = 0.04 s–1) substrates.
Prediction and interpretation of k cat of mutated enzymes
Beyond good overall performance (Fig. 2b), DLKcat was able to capture the effects of amino acid substitutions on the kcat values of individual enzymes. The annotated dataset was divided into wild-type enzymes and mutated enzymes with amino acid substitutions. As the median kcat of mutant enzymes was lower than that of wild-type enzymes (Supplementary Fig. 6a), the deep learning model was a good kcat predictor for both wild-type enzymes (Fig. 3a for the whole dataset; Pearson’s r = 0.87; Supplementary Fig. 6b for the test dataset; Pearson’s r = 0.65) and mutated enzymes (Fig. 3b for the whole dataset; Pearson’s r = 0.90; Supplementary Fig. 6c for the test dataset; Pearson’s r = 0.78). Several well-studied enzyme–substrate pairs were collected from the literature, where each pair had kcat values reported for at least 25 unique single or multiple amino acid substitutions (Supplementary Table 2). The predicted and experimentally measured kcat values correlated very well (Pearson’s r = 0.94; Fig. 3c). The experimentally measured kcat values were further grouped as within a 0.5-fold to 2.0-fold change of wild-type kcat (‘wild-type-like kcat’) or less than a 0.5-fold change of wild-type kcat (‘decreased kcat’). The scarcity of mutated enzymes with kcat values over twofold of the wild-type kcat values precluded defining the ‘increased kcat’ group25,26. DLKcat was able to capture the effects of small changes in protein sequences on the activities of individual enzymes, as the decreased kcat group contained significantly lower predicted kcat values compared to the wild-type-like kcat group, for all enzyme–substrate pairs (Fig. 3d).
a,b, Prediction performance of kcat values for all wild-type (a) and mutated (b) enzymes. Colour brightness represents data density. c, Comparison between predicted and measured kcat values for several well-studied enzyme–substrate pairs with rich experimental mutagenesis data. Enzyme abbreviations: DHFR, dihydrofolate reductase; PGDH, d-3-phosphoglycerate dehydrogenase; AKIII, aspartokinase III; DAOCS, deacetoxycephalosporin C synthase; PNP, purine nucleoside phosphorylase; GGPPs, geranylgeranyl pyrophosphate synthase. Substrate abbreviations: G3P, glycerate 3-phosphate; L-Asp, l-aspartate; IPP, isopentenyl diphosphate. In a–c, the student’s t-test was used to calculate the P value for the Pearson’s correlation. d, Comparison of predicted kcat values on several mutated enzyme–substrate pairs between enzymes with wild-type-like kcat and decreased kcat. P < 0.05 (*), P < 0.01 (**) and P < 0.001 (***), two-sided Wilcoxon rank sum test. Detailed information and sample numbers can be found in Supplementary Table 2. e, Attention weight of residue position in the wild-type PNP enzyme, using inosine as substrate. The mutated residues in each of the mutated enzymes (with both wild-type-like kcat and decreased kcat) were marked on the curve according to their mutated residue. Dot size indicates the number of mutated enzymes with mutations of that residue. f, Overall attention weights for the PNP–inosine pair, comparing enzymes with wild-type-like kcat and decreased kcat by two-sided Wilcoxon rank sum test. n = 15 for wild-type-like kcat; n = 72 for decreased kcat. In each box plot (d and f), the central band represents the median value, the box represents the upper and lower quartiles and the whiskers extend up to 1.5 times the interquartile range beyond the box range.
To investigate which amino acid residues dominate enzyme activity, we applied a neural attention mechanism to back-trace important signals from the neural network output towards its input27. This approach assigns attention weights to each amino acid residue, quantitatively describing its importance for the predicted enzyme activity. Attention weights were calculated for the wild-type H. sapiens purine nucleoside phosphorylase (PNP) with inosine as substrate, as rich mutation data are available for this enzyme–substrate pair28 (Fig. 3e and Supplementary Table 3). Situating the mutations from the wild-type-like kcat and decreased kcat groups (Fig. 3e) to the wild-type PNP sequence exhibited that residues that were mutated in the decreased kcat group had significantly higher attention weights (Fig. 3f; P = 0.0014; Supplementary Table 4). The calculation of attention weights from the deep learning model can thereby identify amino acid residues whose mutation would likely have a more substantial effect on enzyme activity.
The k cat prediction for 343 yeast/fungi species
We previously reconstructed GEMs for 332 yeast species plus 11 out-group fungi, but only expanded 14 of them to ecGEMs using the original pipeline10 due to the limited available kcat data14. As DLKcat allows prediction of almost all kcat values for metabolic enzymes against any substrates for any species, this enabled the generation of ecGEMs for all 343 yeast/fungi species, predicting kcat values for around three million enzyme–substrate pairs (Supplementary Fig. 7). Yeast and fungal specialist enzymes (with narrow substrate specificity) had higher kcat values compared with generalist (that is, promiscuous) enzymes that catalyse more than one reaction in the model (Supplementary Fig. 8a). This is aligned with the hypothesis that ancestral enzymes with broad substrate specificity and low catalytic efficiency improve their kcat value when they evolve into specialists through mutation, gene duplication or horizontal gene transfer29. Sequence conservation also trended with predicted kcat values, where the ratio of non-synonymous over synonymous substitutions (dN/dS) is commonly used to detect proteins undergoing adaptation30. Conserved enzymes with lower dN/dS have significantly higher kcat values compared with relatively lesser conserved enzymes (with high dN/dS), implying that conserved yeast/fungi enzymes under evolutionary pressure are adapted to have higher kcat values (Supplementary Fig. 8b).
Bayesian approach for 343 ecGEM reconstructions
Using the predicted kcat values for 343 yeast/fungi species, we generated 343 ‘DL-ecGEMs’ (ecGEMs parameterized with kcat values from DLKcat). The training data for the deep learning model were primarily measured in vitro, which implies that DLKcat also predicts in vitro kcat values, which is undesired as in vitro kcat values can be considerably different from in vivo31. To resolve these uncertainties, we adopted a Bayesian genome-scale modelling approach32. Here, we used predicted kcat values as mean values for prior distributions and experimentally measured phenotypes to update these to obtain posterior kcat distributions. For this, experimental growth data on yeast/fungi species were collected, collating 371 entries for 53 species with 16 carbon sources (Supplementary Table 5 and Supplementary Fig. 9). A sequential Monte-Carlo-based approximate Bayesian computation (SMC-ABC) approach32 was implemented to sample the kcat values, after validating its generality with the ecGEM of S. cerevisiae, which had the most abundant experimental data (Supplementary Fig. 10). The ecGEMs parameterized with the mean values of sampled posterior kcat values are hereafter represented as posterior-mean-DL-ecGEMs.
The Bayesian learning processes for S. cerevisiae and non-conventional yeast Yarrowia lipolytica are shown as examples (Fig. 4 and Supplementary Fig. 11). We calculated r.m.s.e. values between measurements and predictions for batch and chemostat growth of S. cerevisiae and Y. lipolytica under different carbon sources. After several generations, the ecGEMs parameterized with sampled posterior kcat values achieved a r.m.s.e. lower than one (Fig. 4a and Supplementary Fig. 11a), which showed they could accurately describe the experimental observations. For instance, the S. cerevisiae ecGEM captured the metabolic shift at increasing growth rate (Fig. 4b)—known as the Crabtree effect33—while Y. lipolytica respired at its maximum growth rate (Supplementary Fig. 11b). Principal component analysis for all generated kcat sets (9,800 sets for S. cerevisiae and 4,900 sets for Y. lipolytica) showed a gradual move from the prior distribution to the distinct posterior distribution (Fig. 4c and Supplementary Fig. 11c). The Bayesian learning process affected more variance than mean predicted kcat values (Fig. 4d,e). For S. cerevisiae, 1,057 enzyme–substrate pairs reduced their kcat variance (Šidák-adjusted one-tailed F-test, P < 0.01), while only 532 pairs changed their mean predicted kcat (Šidák-adjusted Welch’s t-test, P < 0.01), which were randomly distributed across metabolic subsystems (Supplementary Table 6; two-sided Fisher’s exact test, P > 0.25). For Y. lipolytica, the values were 1,224 and 646 (Supplementary Fig. 11d,e). Consequentially, the sampled posterior kcat values had a strong correlation with the deep learning-predicted kcat values (Pearson’s r = 0.86 for S. cerevisiae; Fig. 4f; Pearson’s r = 0.83 for Y. lipolytica; Supplementary Fig. 11f).
a, The r.m.s.e. for phenotype measurement and prediction during the Bayesian training process. b, Simulated exchange rates by posterior-mean-ecGEM (lines) compared with experimental data (dots). The kcat values in the posterior-mean-ecGEMs are mean values from 100 sampled posterior datasets obtained from the Bayesian training process. c, Principal component analysis for kcat datasets sampled during the Bayesian training approach, showing the progression from prior to posterior dataset. Each parameter in the set was standardized by subtracting the mean and then divided by the standard deviation before the principal component analysis. In blue are 100 sampled prior datasets; in red are 100 sampled posterior datasets; in grey are all other intermediate datasets. PC, principal component. d, The number of enzymes with a significantly changed mean value (Šidák-adjusted Welch’s t-test, P < 0.01, two-sided) and variance (Šidák-adjusted one-tailed F-test, P < 0.01) between the sampled prior and posterior kcat datasets. Parameters from 126 prior and 100 posterior ecGEMs were used for statistical tests. e, Variance distribution comparison for prior and posterior distribution. f, Correlation between deep learning-predicted kcat and posterior mean kcat. Student’s t-test was used to calculate P value for Pearson’s correlation.
Deep learning and Bayesian approaches improve ecGEM quality
We subsequently generated posterior-mean-ecGEMs from corresponding DL-ecGEMs for all the 343 yeast/fungi species. For comparison, we also built ‘original-ecGEMs’ for the same species with a kcat parameterization strategy that assigns measured kcat values from BRENDA4 and SABIO-RK5 to enzyme/reaction pairs as was done in previous pipelines2,8. We were able to reconstruct original-ecGEMs for all 343 yeast/fungi species only after assuming that orthologs across yeast species had the same EC number annotation as in S. cerevisiae. In case of missing data, certain flexibility was introduced by matching the kcat value to other substrates or organisms, or even introducing wild cards in the EC number. The original-ecGEMs yielded kcat values for ~40% of enzymes and generated enzymatic constraints for ~60% of enzyme-annotated reactions, while DL-ecGEMs and their derived posterior-mean-ecGEMs covered kcat values for ~80% of enzymes and defined enzymatic constraints for ~90% of enzymatic reactions (Fig. 5a,b for 343 yeast/fungi species; Supplementary Fig. 12a,b for S. cerevisiae). While original-ecGEMs had fewer assigned kcat values, their reconstruction pipeline also relied heavily on correct enzyme EC number annotations and available measured kcat values in the databases, contrasting with the DL-ecGEM reconstruction, which relied only on protein sequences and substrate SMILES information while resulting in a higher coverage. In DL-ecGEMs and posterior-mean-ecGEMs the only missing kcat values were for generic substrates without defined SMILES information (such as generic compounds phosphatidate and thioredoxin).
a,b, Enzymatic constraint coverage comparison for enzymes (a) and enzymatic reactions (b) of 343 yeast/fungi species. c, The r.m.s.e. for the phenotype prediction for 53 species with phenotype data. d, Growth prediction of posterior-mean-ecGEMs for 53 species with phenotype data. e, Performance of three types of ecGEMs in predicting quantitative proteome data: the original-ecGEM, DL-ecGEM and posterior-mean-ecGEM are shown. Four species with absolute proteome data were evaluated. Original-ecGEMs were constructed following the pipeline to extract kcat profiles from BRENDA and SABIO-RK; DL-ecGEMs were constructed from DLKcat-predicted kcat profiles; and posterior-mean-ecGEMs were parameterized with mean kcat values from 100 posterior datasets after the Bayesian training process. Culture conditions for the labels on the x axis of those proteome datasets can be found in Supplementary Table 7, and the collected proteome datasets are available in the GitHub repository. sce, S. cerevisiae; kla, Kluyveromyces lactis; kmx, Kluyveromyces marxianus; yli, Y. lipolytica. DL, deep learning-predicted. In the violin plot (a, b and c), white shaded box limits stands for the upper and lower quartiles; the central line limits stands for the 1.5× interquartile range.
Besides the improved kcat coverage, the posterior-mean-ecGEMs and DL-ecGEMs also outperformed original-ecGEMs in the prediction of exchange rates (Fig. 5c for 53 species with reported phenotype; Supplementary Fig. 12c for S. cerevisiae) and maximum growth rates under various carbon sources and oxygen availabilities (Fig. 5d and Supplementary Fig. 13 for 53 species with reported growth phenotype; Supplementary Fig. 12d for S. cerevisiae). Moreover, we used these three types of ecGEMs to predict required protein abundances and compared this with published quantitative proteomics data from four species with different carbon sources, culture modes and medium set-ups (Supplementary Table 7). Proteome predictions from DL-ecGEMs and posterior-mean-ecGEMs had the lowest r.m.s.e. values, while DL-ecGEMs had already reduced the r.m.s.e. by 30% when compared to original-ecGEMs (Fig. 5e for four species with absolute proteome data). Combined, the current pipeline not only increases kcat coverage but also contributes to ecGEMs better representing the 343 fungi/yeast species.
The k cat comparison identifies phenotype-related enzymes
The predicted kcat values were furthermore able to distinguish between Crabtree positive and negative yeast species. There is much interest in understanding the presence of the Crabtree phenotype among yeast species34,35, and a model of S. cerevisiae energy metabolism has previously been used to interpret this phenotype by comparing protein efficiency (that is, ATP produced per protein mass per time) in its two energy-producing pathways1. It was postulated that the Crabtree effect is related to the high-yield (HY) pathway (containing the Embden–Meyerhof–Parnas pathway, the tricarboxylic acid (TCA) cycle and the electron transport chain), having a lower protein efficiency than the low-yield (LY) pathway (containing Embden–Meyerhof–Parnas plus ethanol formation; Fig. 6a)1. We here used the posterior-mean-ecGEMs of 102 yeast species with experimental reported Crabtree phenotype (25 positive; 77 negative) to similarly calculate the protein efficiencies of the HY and LY pathways. Of the 102 species, 89% followed the trend that Crabtree positive species have a higher LY efficiency, suggesting that Crabtree positive yeasts’ LY pathways are more protein efficient than their HY pathways for producing the same amount of ATP (Supplementary Table 8). For five commonly studied species, the results are shown in Fig. 6b, and even though ATP yields in their HY pathways may vary across species, primarily due to the presence of respiratory complex I, they still followed the same trend (Supplementary Table 8). Inconsistencies in strains where the HY/LY protein efficiency ratio did not trend with the Crabtree effect might be due to additional regulation not considered in ecGEMs36.
a, HY and LY pathway definitions. PEP, phosphoenolpyruvate; PYR, pyruvate; OAA, oxaloacetate; CIT, citrate; ETC, electron transport chain. b, Model-inferred protein efficiency of energy metabolism in several common yeast species. Protein efficiency is the ATP produced per protein mass per unit time, in units of millimoles ATP per grams protein per hour. L. kluyveri, Lachancea kluyveri. c, Enzymes with significantly different kcat values between Crabtree positive and negative species. A two-sided Wilcoxon rank sum test was used to calculate P values. Crabtree positive species (n = 25) and Crabtree negative species (n = 77) were examined in this analysis. In the box plot, the central band represents the median value, the box represents the upper and lower quartiles and the whiskers extend up to 1.5 times the interquartile range beyond the box range.
With the predicted kcat profiles for yeast species, we could investigate whether key enzymes show different kcat values among 25 Crabtree positive and 77 negative species. Of the enzymes in the energy-producing pathways, only pyruvate kinase, citrate synthase, fumarase and phosphoglucose isomerase had significantly different kcat values (Fig. 6c). Since fumarase and phosphoglucose isomerase can operate in reversible directions, it is unclear how the kcat difference relates to the Crabtree effect. The kcat values of pyruvate kinase were higher in Crabtree positive species (P = 0.006; Fig. 6c). This aligns with the fact that increasing pyruvate kinase activity in the Crabtree positive Schizosaccharomyces pombe increases its fermentation ratio, decreases the growth dependence on respiration and provides resistance to growth-inhibiting effects of antimycin A, which inhibits respiratory complex III (ref. 37). Citrate synthase catalyses the first and rate-limiting step of the TCA cycle38, condensing acetyl-coenzyme A and oxaloacetate to citrate. The kcat values of citrate synthase of Crabtree negative species are higher (P = 0.008), which would benefit metabolic flux from entering the TCA cycle (Fig. 6a,c). This is consistent with 13C-metabolic flux analysis that showed that Crabtree negative species have higher TCA flux39,40.
Discussion
The diversity of biochemical reactions and organisms makes it difficult to generate genome-scale kcat profiles. Here we presented the deep learning approach DLKcat to predict kcat values of all metabolic enzymes against their substrates, requiring only the substrate SMILES information and protein sequences of the enzymes as input, yielding a versatile kcat prediction tool for any species.
DLKcat can capture kcat changes towards precise single amino acid substitutions, enabling attention weight calculations that identify the amino acid residues majorly impacting enzyme activity. Amino acid substitution is a powerful technique in the enzyme evolution field and routinely used to probe enzyme catalytic mechanisms41,42. Particularly, most substitution experiments perform mutagenesis in the substrate binding site region, since it is hypothesized that the binding region would have a high impact towards catalytic activity. However, it has been reported that remote regions can have a profound impact on catalytic activity43,44. Here, we identified not only high attention weights for amino acid residues in the inosine binding region of human PNP enzyme, but also various non-binding residue sites with high attention weights, suggesting that those residues may also majorly impact catalytic activity and deserve further validation. DLKcat can thereby serve as a valuable part of the protein engineering toolbox45,46.
Predicted genome-scale kcat profiles can facilitate the reconstruction of enzyme-constrained models of metabolism, from both curated and automatically generated basic (non-ec) GEMs. The deep learning-predicted kcat process proved to be a more comprehensive but still practical alternative to matching in vitro kcat values from the BRENDA4 and SABIO-RK5 databases, as is common in original-ecGEM reconstruction pipelines such as the GECKO and MOMENT2,8,47. By not depending on EC number annotation, DLKcat is furthermore able to predict isozyme-specific kcat values, while the use of SMILES (matching via the PubChem48 or MetaNetX49 databases) avoids the issues of ununified substrate naming between the GEM and BRENDA that original-ecGEM reconstruction pipelines can experience. The DL-ecGEMs can subsequently be adjusted to existing experimental growth data through a Bayesian approach that yields posterior-mean-ecGEMs with physiologically relevant solution spaces. Combined, the current DLKcat-based pipeline is therefore applicable to ecGEM reconstruction for virtually any organism for which a protein sequence FASTA file and a basic GEM is available. Our pipeline hereby improves applicability, and it even improves the number of reactions with enzymatic constraints in comparison with original-ecGEMs that have previously been constructed2,8,9,10,11,12,50.
Even though the DLKcat-based pipeline yields ecGEMs with superior performance over original-ecGEMs, various challenges remain. For example, while our deep learning model can distinguish alternative from randomly chosen substrates for promiscuous enzymes (Fig. 2c), it still predicts a level of kinetic activity towards random substrates that is likely too high. This behaviour can be explained by the limited availability of negative data: cases where an enzyme–substrate pair did not result in catalysis. Increased reporting of negative datasets, where non-detected activity for enzyme–substrate pairs are reported and collected by enzyme databases, could enhance future deep learning models in terms of defining true negatives46. In addition, DLKcat did not consider the effect of environmental factors such as pH and temperature, but combining DLKcat with other emerging machine learning tools, such as for enzyme optimal temperature prediction, would enable future investigation on the impact of environmental parameters on enzyme activities32.
Another challenge relates to reactions involving multiple substrates and those catalysed by heteromeric enzyme complexes. The multiple substrate SMILES and protein sequences that can be defined for such reactions can all function with DLKcat, thereby yielding multiple predicted kcat values for one reaction. We currently select the maximum kcat values in those cases, but it would be favourable to devise an approach that can predict one kcat value for each multi-substrate and/or heteromeric enzyme.
In addition, DLKcat-derived DL-ecGEMs and posterior-mean-ecGEMs inherit limitations from basic (non-ec) GEMs, where the steady-state assumption that is central to constraint-based modelling allows one to determine metabolic fluxes but does not readily consider regulatory behaviours. While ecGEMs drastically reduce the solution space of constraint-based models to cellular feasible capacities, kcat is not the only kinetic parameter that determines reaction rate, as for example, affinity constants play influential roles. However, as constraint-based models cannot predict internal metabolite concentrations, it is currently not feasible to readily consider the influence of those parameters. Nonetheless, kcat values are also important parameters in other resource allocation models such as proteome-constrained GEMs51,52,53 and metabolism/macromolecular-expression models7,54,55. Despite improved predictions and more applications, how to define kcat values has also remained a challenge in the reconstruction of those models. Such resource allocation models and ecGEMs share the assertion that cells need to allocate their limited proteome to different pathways to achieve faster growth or better fitness, while the proteome cost for each reaction is similarly defined by the flux and the kinetic rate of the enzyme. Deep learning-predicted kcat values for the metabolic parts of those models can therefore improve their quality and performance, although other challenging kinetic parameters, for example, ribosomal catalytic rates, to be determined in those model formulations cannot be obtained from DLKcat. In addition, model formulations that particularly focus on describing enzyme kinetics56 could benefit from deep learning-predicted kcat values, so that our DLKcat approach can find a broad application in the modelling field.
In conclusion, we showed that DLKcat yields realistic kcat values that can be used to direct future genetic engineering, understand enzyme evolution and reconstruct ecGEMs to predict metabolic fluxes and phenotypes. Besides that, we envision many other possible uses of this deep learning-based kcat prediction tool, such as a tool in genome mining and Genome-Wide Association Studies analysis. The developed automatic Bayesian ecGEM reconstruction pipeline will be instrumental for further use in ecGEM reconstruction, for omics data incorporation and analysis.
Methods
Dataset preparation for deep learning model development
The dataset used for deep learning model construction was extracted from the BRENDA4 and SABIO-RK databases5 on 10 July 2020 by customized scripts via application programming interface. We generated a comprehensive dataset including the substrate name, organism information, EC number, protein identifier (UniProt ID), enzyme type and kcat values. As the overall majority of kcat values reported in BRENDA and SABIO-RK do not specify their assay conditions, such as pH and temperature, we decided not to include the features in order to maintain the training dataset size and variety. In addition, substrate SMILES, a string notation to represent the substrate structure, was extracted using substrate name to query the PubChem compound database48, which is the largest database of chemical compound information and is easy to access57. As different substrates usually have various synonyms in different databases and GEMs, we used a customized Python-based script to ensure that the same canonical SMILES information could be output for the same substrates with various synonyms, which is essential to help filter redundant entries obtained from different databases. Several rounds of data cleaning were performed to ensure quality (Supplementary Fig. 2). Protein sequences were queried with two methods: for entries with UniProt ID information, the amino acid sequences could be obtained via the application programming interface of the UniProt58 with the help of Biopython v.1.78 (https://biopython.org/); and for entries without UniProt ID, the amino acid sequences were acquired from the UniProt58 and the BRENDA4 databases based on their EC number and organism information. After that, the sequences of those entries with wild-type enzymes were mapped directly, and the sequences of those entries with mutated enzymes were changed according to the mutated sites. Finally, the remaining entries formed the high-quality dataset for deep learning model construction. Detailed numbers for the data cleaning can be found in Supplementary Fig. 2.
Construction of the deep learning pipeline
In this work, we developed an end-to-end learning approach for in vitro kcat value prediction by combining a GNN for substrates and a CNN for proteins. The integration of GNN and CNN can be naturally used to handle pairs of data with different structures, that is, molecular graphs and protein sequences. In this approach, substrates are represented as molecular graphs where the vertices are atoms and the edges are chemical bonds, while proteins are represented as sequences in which the characters are amino acids.
For substrates, there are just a few types of chemical atoms (for example, carbon and hydrogen) and chemical bonds (for example, single bond and double bond). To obtain more learning parameters, we employed r-radius subgraphs to get the vector representations, which are induced by the neighbouring vertices and edges within radius r from a vertex59. First, substrate SMILES information was converted to a molecular graph using RDKit v.2020.09.1 (https://www.rdkit.org). Given a substrate graph, the GNN can update each atom vector and its neighbouring atom vectors transformed by the neural network via a nonlinear function, for example, ReLU (ref. 60). In addition, two transitions were developed in the GNN, including vertex transitions and edge transitions. The aim of transitions is to ensure that the local information of vertices and edges is propagated in the graph by iterating the process and summing neighbouring embeddings. The final output of the GNN is a set of real-valued molecular vector representations for substrates.
Similarly, by using the CNN to scan protein sequences, we can obtain low-dimensional vector representations for protein sequences transformed by the neural network via a nonlinear function, for example, ReLU. To apply the CNN to proteins, we defined ‘words’ in protein sequence and split a protein sequence into an overlapping n-gram (n = 1, 2, 3) of amino acids61. In this work, to avoid low-frequency words in the learning representations, a relatively smaller n-gram number of 1, 2 or 3 was set. Then, we translated protein sequences into various word embeddings. Following this, the CNN used a filter function, shown in equation (1), to compute the hidden vectors from the input word embeddings and weight matrix. After that, we obtained a set of hidden vectors for these split subsequences based on n-gram amino acid splitting.
where f is a nonlinear activation function (for example, ReLU); Wconv is the weight matrix and bconv is the bias vector; i and t are the serial numbers of a set of hidden vectors; and ci(t) and ci(t–1) are the hidden vectors for the protein sequence.
Also, other important parameters of the neural networks (CNN and GNN) were set as follows: number of convolutional layers in CNN, 2, 3 or 4; number of time steps in GNN, 2, 3 or 4; window size, 11 (fixed); r-radius, 0, 1 or 2; and vector dimensionality, 5, 10 or 20. These different settings were explored based on the coefficient of determination (R2) in equation (2) during the hyperparameter tuning to find which hyperparameter is better for improving the deep learning performance. The R2 was calculated by scikit-learn v.0.23.2 (https://scikit-learn.org/stable/). And finally, we used the optimal hyperparameters to train our deep learning model.
where yip is the predicted kcat value, yie is the experimental kcat value, \(\bar{y}\) is the average of the experimental kcat values and n is the total number of items in the dataset (validation dataset or test dataset).
After the acquisition of the substrate molecular vector representations and the protein sequence vector representations, we concatenated them together along with an output vector (kcat value) to train the deep learning model using the neural attention mechanism59. During the training process, all the datasets were shuffled at the first step, and then were randomly split into a training dataset, validation dataset and test dataset at the ratio of 80%:10%:10%. Given a set of substrate–protein pairs and the kcat values in the training dataset, the aim of the training process is to minimize its loss function. The best model was chosen according to the minimal r.m.s.e., shown in equation (3), on the validation dataset with the least spread between the training dataset and validation dataset. For building and training models, the PyTorch v.1.4.0 software package was used and accessed using the Python package v.3.7.6 interface under CUDA/10.1.243. In addition, data processing was mainly implemented by NumPy v.1.20.2, SciPy v.1.5.2 and pandas v.1.1.3. Data visualization was implemented by Matplotlib v.3.3.2 and seaborn v.0.11.0.
where yip is the predicted kcat value, yie is the experimental kcat value and n is the total number of items in the dataset (validation dataset or test dataset).
Enzyme promiscuity analysis based on deep learning model
For enzyme promiscuity, we explored whether the deep learning model can identify substrate preference for promiscuous enzymes. For each promiscuous enzyme, we defined that the substrate with the highest kcat value was considered as the preferred substrate, while those with kcat values less than the maximum value were classified as alternative substrates. Random substrates were randomly chosen from the compound dataset in our training data, except for the documented substrates and products for the tested enzyme. By using the deep learning model, we further predicted and compared the kcat values for the preferred, alternative and random substrates on various promiscuous enzymes. In order to identify high-quality promiscuous enzymes, entries with an experimentally measured kcat value less than –2 (s–1) in a log10 scale were excluded in this analysis.
Validation of deep learning-based k cat values
According to the classification of metabolic pathways, metabolic contexts were mainly divided into four different subsystems: (1) primary metabolism (carbohydrate and energy), involving the main carbon and energy metabolism, for example, glycolysis/gluconeogenesis, TCA cycle, pentose phosphate pathway, and so on; (2) primary metabolism (amino acids, fatty acids and nucleotides); (3) intermediate metabolism, related to the biosynthesis and degradation of cellular components, such as coenzymes and cofactors; and (4) secondary metabolism6. To explore the metabolic subsystems for all of the wild-type enzymes in the experimental dataset, the module in the KEGG database62 was used to assign metabolic pathways for enzyme–substrate pairs by linking the detailed metabolic pathway in the KEGG application programming interface with the EC number annotated in each enzyme–substrate pair. Detailed classification can be found in Supplementary Table 1. Using the trained deep learning model, the predicted kcat values were generated for all the enzyme–substrate pairs.
Interpretation of the reasoning of deep learning
To interpretate which subsequences or residue sites are more important for the substrate, the neural attention mechanism was employed by assigning attention weights to the subsequences27. A higher attention weight of one residue means that that residue is more important for the enzyme activity towards the specific substrate. Such attention weights were modelled based on the output of the neural network. The mathematical equations for the neural attention mechanism are shown as follows:
where C is a set of hidden vectors for the protein sequence, c1(t) to cn(t) are the sub-hidden vectors for the split subsequences, ysubstrate is the substrate molecular vector, Winter and b are the weight matrix and the bias vector in the neural network, respectively, f is a nonlinear activation function (for example, ReLU), αi is the final attention weight value, σ is the element-wise sigmoid function, and T is the transpose function.
A defined protein could be split into overlapping n-gram amino acids and calculated as a set of hidden vectors in equation (4). Given a substrate molecular vector ysubstrate and a set of protein hidden vectors, the substrate embeddings (hsubstrate) and subsequence embeddings (hi) could be output based on the neural network, as shown in equations (5) and (6). By considering the embeddings of ysubstrate, the attention weight value for each subsequence was accessible in equation (7), which represents the importance signals of the protein subsequence towards the enzyme activity for a certain substrate.
Prediction of k cat values for 343 yeast/fungi species
The GEMs of 343 yeast/fungi species were automatically reconstructed in our previous paper14 from a yeast/fungi ‘pan-GEM’, which was derived from the well-curated Yeast8 of S. cerevisiae combined with the pan-genome annotation. For each model, all reversible enzymatic reactions were split into forward and backward reactions. Reactions catalysed by isoenzymes were also split into multiple reactions with one enzyme complex for each reaction. Substrates were extracted from the model and mapped to the MetaNetX database to get SMILES information using annotated MetaNet identifiers (IDs) for metabolites49. Protein IDs for the enzymes were from the model grRules. Protein sequences were queried by the protein ID in the protein FASTA file for each species. Reaction IDs, substrate names, substrate SMILES information and protein IDs were combined as the input file for the deep learning kcat prediction model.
Analysis of k cat values and dN/dS for yeast/fungi species
In a previous study, the genomes of 343 yeast/fungi species combined with comprehensive genome annotations were publicly available63. The gene-level dN/dS of gene sequences for pairs of orthologous genes from the 343 species were calculated with yn00 from PAML v.4.7 (ref. 64). For this computational framework, the input is the single-copy ortholog groups, and the output is the gene-level dN/dS values extracted from the PAML output files. By mapping the predicted kcat values with the gene-level dN/dS values via the bridge of protein ID, a global analysis was performed between the kcat values and the dN/dS values for 343 yeast/fungi species across the out-group (11 fungal species) together with 12 major clades divided by the genus-level phylogeny for 332 yeast species.
ecGEM reconstruction
Besides the constraints in basic (non-ec) GEM, shown in equations (8) and (9), ecGEMs are reconstructed by adding enzymatic constraints, shown in equations (10) and (11).
in which S is the stoichiometry matrix and v is the flux vector. This equation is the representative of the steady-state assumption of the metabolic model to constrain the mass balance.
in which lb and ub are the lower bound and upper bound of the rate for the reaction j.
where vj stands for the metabolic flux (mmol gDW–1 h–1; gDW, gram dry weight) of the reaction j; [Ei] stands for the enzyme concentration for the enzyme i that catalyses reaction j; and \(k_{{\mathrm{cat}}}^{i,j}\) is the catalytic turnover number for the enzyme catalysing reaction j. This constraint is applied to all enzymatic reactions with available kcat values. Additionally, we added reactions to draw protein mass from the total protein pool to each enzyme, therefore, a mass balance constraint was proposed as:
where θ is the fraction of metabolic protein in the total protein content of the cell. This equation means that the sum enzyme usage should be lower or equal to the total metabolic protein abundance.
To compare the different kcat value assignment approaches, we built ecGEMs parameterized with three types of kcat values: original-ecGEMs, DL-ecGEMs and posterior-mean-ecGEMs.
Original-ecGEM reconstruction queried kcat values from the BRENDA database by matching the EC number, a method that relies heavily on the database EC number annotation for the specific species2,8. Since more than 200 out of 343 yeast/fungi species are not annotated in UniProt58 and KEGG62, EC numbers for orthologs annotated in S. cerevisiae were borrowed to facilitate the original-ecGEM reconstruction process for all these 343 species. The kcat extraction process used the criteria from process 13 in the reconstruction methods of the reference47.
DL-ecGEM reconstruction extracted all kcat values from the deep learning predicted file. To assign a kcat value for each metabolic reaction, we followed these criteria: If the in vitro kcat measurement with matched substrate and enzyme was available, then the measured in vitro kcat values were used rather than the kcat prediction. This pipeline also accepted the user’s input for the kcat values. For enzymes with no kcat measurement, predicted kcat values were used after the following steps: kcat values predicted for currency metabolites such as H2O and H+ were excluded; if there were multiple substrates in the reaction, maximum values among the substrates were kept; and if multiple subunits existed in the enzyme complex, we used the maximum value among all subunits to represent the kcat for the complex. Subunit protein stoichiometry information was multiplied before comparison. We assumed the same enzyme complex stoichiometry information for yeast species as that of S. cerevisiae, which is collected from the Protein Data Bank in Europe database (https://www.ebi.ac.uk/pdbe/) as well as the Complex Portal (www.ebi.ac.uk/complexportal).
Posterior-mean-ecGEM reconstruction was parameterized by mean kcat values from accepted posterior distribution. The kcat values in the DL-ecGEMs combined with the r.m.s.e. (which is 1 in the log10 scale) of the kcat prediction were used as mean values and variance to make the prior distribution. Each kcat value was described with a log normal distribution N(kcati, 1). This prior iteratively morphs into a posterior through multiple generations32. For each generation, we sampled 126 kcat datasets within the distribution; 100 among those 126 datasets with a smaller distance (see next section for the SMC-ABC distance calculation) between the phenotype measurements and predictions, which can better represent the phenotype, were kept to make the distribution for the next generation. Until the distance was lower than the cut-off (r.m.s.e. for phenotype prediction of 1), we accepted the final distribution as the posterior distribution32.
SMC-ABC distance function
Experimental growth data and related exchange rates in batch and chemostat conditions were collected for the yeast/fungi species, which are available in Supplementary Table 5. The distance function was designed as the r.m.s.e. between the simulated and experimental phenotypes. To have a metric for the variance of phenotype prediction of both flux and maximum growth potential, r.m.s.e. was designed in two parts (each part may contain multiple measurement entries such as growth with a different medium). The first part addressed flux prediction. This part checks whether the model predicts similar fluxes when the carbon uptake rate is constrained, as experimentally measured. In this part, all data points for the species are used, and all measured exo-metabolite exchange fluxes are used for comparison. The second part addresses the prediction of the maximum growth rate potential. This part checks the maximum growth rate of the model prediction against the experimental measurement for one species on a certain experimentally tested medium. In this part, only the batch condition with maximum growth rate measurement was tested. No carbon uptake rate or other exchange rate was constrained in the model. Growth maximization was set as the objective function. After simulation, only the maximum growth rate and the carbon uptake rates were used for comparison with measurement.
After running the above two parts of the simulations, the r.m.s.e. for each part can be calculated. All measured and simulated rates were normalized by multiplying the carbon numbers of the corresponding metabolites before calculation of r.m.s.e. The carbon number for biomass is 41 (the mean value for the molecular weight of 1 carbon moles (Cmol) biomass of yeast is ~24.42 g (ref. 65); the biomass equals 1,000 mg). Note that if the substrate or by-product does not contain any carbon, such as O2, then the normalizing number is 1. Then the average r.m.s.e. of both simulations was used to represent the distance. The SMC-ABC search stopped once the r.m.s.e. reached the accepted value or reached the maximum generation. The accepted value for the distance was set to be lower than 1, and the maximum generation was set to be 100.
Simulations with ecGEMs
We performed different kinds of simulations using the ecGEMs, including simulations of growth and protein abundance. Different media and growth conditions were set to match the experiment measurement conditions, for example, using xylose as the carbon source or anaerobic conditions. Since there are no measured total protein abundances in the biomass for all yeast/fungi species, we used the protein content mass to serve as the default total protein abundance for each species and used a factor of 0.5 to serve as the ratio of the metabolic protein to the total protein.
As for the protein abundance simulation, the medium was set to match the experimental condition as mentioned above. For the chemostat condition, the growth rate was fixed as the dilution rate, and the carbon source uptake rate was minimized, which is a normal set-up for the simulation of the chemostat condition. For the batch condition, the growth rate maximization was used as the objective. Then, the simulated protein abundances, which can be extracted from the fluxes, were compared with those in collected proteome datasets. The MATLAB (2019b), COBRA (v.3.2)66, RAVEN (v.2.4)67 and libSBML (v.5.17.0) toolboxes were used in the process with solver IBM ILOG CPLEX optimizer. Violinplot-Matlab (https://github.com/bastibe/Violinplot-Matlab) was used for the visualization of violin plots.
Statistical tests for Bayesian approach
Sampled prior and posterior kcat datasets were compared for the difference in the mean values and the variance. Welch’s t-test was used to test the significance for the mean values, while a one-tailed F-test was used for the reduced variances. The cut-off for the significance was set to 0.01 for the adjusted P value corrected by the Šidák method. PVAL_ADJUST (https://github.com/nunofachada/pval_adjust) was used in the analysis.
Proteome data processing
We normalized the collected relative proteome datasets using the identical condition of the absolute proteome data from the literature following the same method as in ref. 68. The reference absolute datasets for those relative proteome datasets were documented in the collected file in the GitHub repository.
Calculation of protein cost and efficiency
To calculate the protein cost of the HY pathway, the glucose uptake rate was fixed at 1 mmol gDW–1 h–1, and the non-growth associated maintenance energy (NGAM) reaction was maximized. The total protein pool reaction was then minimized by fixing the NGAM reaction at the maximized value. The minimized flux through the total protein pool reaction is the protein cost of the HY pathway for converting one glucose to ATP. As for the protein cost calculation of the LY pathway, the glucose uptake rate was fixed at 1 mmol gDW–1 h–1, and ethanol production was maximized. Then the ethanol exchange rate was fixed at the maximized value, and NGAM was maximized. After that, NGAM was also fixed at the maximized value, and the total protein pool was minimized to calculate the protein cost for the LY pathway. We also examined the flux distribution to ensure that other energy-producing pathways were all inactive during this simulation. Protein efficiency is defined as the protein cost for producing one flux ATP in each pathway.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
Protein sequence FASTA files, deep learning predicted kcat values, GEMs, original-ecGEMs, DL-ecGEMs and posterior-mean-ecGEMs for 343 yeast/fungi species are available as a supplementary dataset on Zenodo: https://doi.org/10.5281/zenodo.6438262. Collected proteome data are available in the GitHub repository: https://github.com/SysBioChalmers/DLKcat/tree/master/BayesianApporach/Data/Proteome_ref.xlsx. All other collected datasets such as the training dataset and the deep learning model are available in the GitHub repository: https://github.com/SysBioChalmers/DLKcat. Databases including BRENDA (https://www.brenda-enzymes.org), SABIO-RK (http://sabiork.h-its.org/), UniProt database (https://www.uniprot.org/) and PubChem (https://pubchem.ncbi.nlm.nih.gov) were used in the DLKcat model construction. KEGG (http://www.kegg.jp/) was used in the evaluation of the DLKcat performance. Databases including the MetaNetX database (https://www.metanetx.org/), the Protein Data Bank in Europe database (https://www.ebi.ac.uk/pdbe/) and the Complex Portal (https://www.ebi.ac.uk/complexportal) were used in the ecGEM reconstruction. The authors declare that all data supporting the findings and for reproducing all figures of this study are available within the paper and its Supplementary Information. Source data are provided with this paper.
Code availability
To facilitate further usage, we provide all codes and detailed instruction in the GitHub repository: https://github.com/SysBioChalmers/DLKcat. A user-friendly example for kcat prediction is also included in the repository.
References
Chen, Y. & Nielsen, J. Energy metabolism controls phenotypes by protein efficiency and allocation. Proc. Natl Acad. Sci. USA 116, 17592–17597 (2019).
Sánchez, B. J. et al. Improving the phenotype predictions of a yeast genome‐scale metabolic model by incorporating enzymatic constraints. Mol. Syst. Biol. 13, 935 (2017).
Klumpp, S., Scott, M., Pedersen, S. & Hwa, T. Molecular crowding limits translation and cell growth. Proc. Natl Acad. Sci. USA 110, 16754–16759 (2013).
Schomburg, I. et al. The BRENDA enzyme information system–from a database to an expert system. J. Biotechnol. 261, 194–206 (2017).
Wittig, U., Rey, M., Weidemann, A., Kania, R. & Müller, W. SABIO-RK: an updated resource for manually curated biochemical reaction kinetics. Nucleic Acids Res. 46, D656–D660 (2018).
Bar-Even, A. et al. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 50, 4402–4410 (2011).
Chen, Y. & Nielsen, J. Mathematical modelling of proteome constraints within metabolism. Curr. Opin. Syst. Biol. 25, 50–56 (2021).
Bekiaris, P. S. & Klamt, S. Automatic construction of metabolic models with enzyme constraints. BMC Bioinf. 21, 19 (2020).
Ye, C. et al. Improving lysine production through construction of an Escherichia coli enzyme‐constrained model. Biotechnol. Bioeng. 117, 3533–3544 (2020).
Domenzain, I. et al. Reconstruction of a catalogue of genome-scale metabolic models with enzymatic constraints using GECKO 2.0. Preprint at bioRxiv https://doi.org/10.1101/2021.03.05.433259 (2021).
Yeo, H. C., Hong, J., Lakshmanan, M. & Lee, D.-Y. Enzyme capacity-based genome scale modelling of CHO cells. Metab. Eng. 60, 138–147 (2020).
Robinson, J. L. et al. An atlas of human metabolism. Sci. Signal. 13, eaaz1482 (2020).
Nilsson, A., Nielsen, J. & Palsson, B. O. Metabolic models of protein allocation call for the kinetome. Cell Syst. 5, 538–541 (2017).
Lu, H. et al. Yeast metabolic innovations emerged via expanded metabolic network and gene positive selection. Mol. Syst. Biol. 17, e10427 (2021).
Davidi, D. & Milo, R. Lessons on enzyme kinetics from quantitative proteomics. Curr. Opin. Biotechnol. 46, 81–89 (2017).
Heckmann, D. et al. Machine learning applied to enzyme turnover numbers reveals protein structural correlates and improves metabolic models. Nat. Commun. 9, 5252 (2018).
Kitchin, J. R. Machine learning in catalysis. Nat. Catal. 1, 230–232 (2018).
Shrivastava, A. D. & Kell, D. B. FragNet, a contrastive learning-based transformer model for clustering, interpreting, visualizing, and navigating chemical space. Molecules 26, 2065 (2021).
Zrimec, J. et al. Deep learning suggests that gene expression is encoded in all parts of a co-evolving interacting gene regulatory structure. Nat. Commun. 11, 6141 (2020).
Kroll, A., Engqvist, M. K. M., Heckmann, D. & Lercher, M. J. Deep learning allows genome-scale prediction of Michaelis constants from structural features. PLoS Biol. 19, e3001402 (2021).
Ryu, J. Y., Kim, H. U. & Lee, S. Y. Deep learning enables high-quality and high-throughput prediction of enzyme commission numbers. Proc. Natl Acad. Sci. USA 116, 13996–14001 (2019).
Notebaart, R. A., Kintses, B., Feist, A. M. & Papp, B. Underground metabolism: network-level perspective and biotechnological potential. Curr. Opin. Biotechnol. 49, 108–114 (2018).
Kuznetsova, E. et al. Genome-wide analysis of substrate specificities of the Escherichia coli haloacid dehalogenase-like phosphatase family. J. Biol. Chem. 281, 36149–36161 (2006).
Notebaart, R. A. et al. Network-level architecture and the evolutionary potential of underground metabolism. Proc. Natl Acad. Sci. USA 111, 11762–11767 (2014).
Yep, A., Kenyon, G. L. & McLeish, M. J. Saturation mutagenesis of putative catalytic residues of benzoylformate decarboxylase provides a challenge to the accepted mechanism. Proc. Natl Acad. Sci. USA 105, 5733–5738 (2008).
Lin, Y.-H. T., Huang, C. L. V., Ho, C., Shatsky, M. & Kirsch, J. F. A general method to predict the effect of single amino acid substitutions on enzyme catalytic activity. Preprint at bioRxiv https://doi.org/10.1101/236265 (2017).
Bahdanau, D., Cho, K. & Bengio, Y. Neural machine translation by jointly learning to align and translate. Preprint at https://doi.org/10.48550/arXiv.1409.0473 (2014).
Erion, M. D. et al. Purine nucleoside phosphorylase. 1. Structure-function studies. Biochemistry 36, 11725–11734 (1997).
Nam, H. et al. Network context and selection in the evolution to enzyme specificity. Science 337, 1101–1104 (2012).
Kryazhimskiy, S. & Plotkin, J. B. The population genetics of dN/dS. PLoS Genet. 4, e1000304 (2008).
Ringe, D. & Petsko, G. A. Biochemistry. How enzymes work. Science 320, 1428–1429 (2008).
Li, G. et al. Bayesian genome scale modelling identifies thermal determinants of yeast metabolism. Nat. Commun. 12, 190 (2021).
Van Hoek, P. I. M., Van Dijken, J. P. & Pronk, J. T. Effect of specific growth rate on fermentative capacity of baker’s yeast. Appl. Environ. Microbiol. 64, 4226–4233 (1998).
Pfeiffer, T. & Morley, A. An evolutionary perspective on the Crabtree effect. Front. Mol. Biosci. 1, 17 (2014).
de Alteriis, E., Cartenì, F., Parascandola, P., Serpa, J. & Mazzoleni, S. Revisiting the Crabtree/Warburg effect in a dynamic perspective: a fitness advantage against sugar-induced cell death. Cell Cycle 17, 688–701 (2018).
Ata, Ö. et al. A single Gal4-like transcription factor activates the Crabtree effect in Komagataella phaffii. Nat. Commun. 9, 4911 (2018).
Kamrad, S. et al. Pyruvate kinase variant of fission yeast tunes carbon metabolism, cell regulation, growth and stress resistance. Mol. Syst. Biol. 16, e9270 (2020).
Krebs, H. A. Rate control of the tricarboxylic acid cycle. Adv. Enzym. Regul. 8, 335–353 (1970).
Christen, S. & Sauer, U. Intracellular characterization of aerobic glucose metabolism in seven yeast species by 13C flux analysis and metabolomics. FEMS Yeast Res. 11, 263–272 (2011).
Blank, L. M., Lehmbeck, F. & Sauer, U. Metabolic-flux and network analysis in fourteen hemiascomycetous yeasts. FEMS Yeast Res. 5, 545–558 (2005).
Chen, K. & Arnold, F. H. Engineering new catalytic activities in enzymes. Nat. Catal. 3, 203–213 (2020).
Markel, U. et al. Advances in ultrahigh-throughput screening for directed enzyme evolution. Chem. Soc. Rev. 49, 233–262 (2020).
Loeb, D. D. et al. Complete mutagenesis of the HIV-1 protease. Nature 340, 397–400 (1989).
Lee, J. & Goodey, N. M. Catalytic contributions from remote regions of enzyme structure. Chem. Rev. 111, 7595–7624 (2011).
Tong, H., Küken, A., Razaghi-Moghadam, Z. & Nikoloski, Z. Characterization of effects of genetic variants via genome-scale metabolic modelling. Cell. Mol. Life Sci. 78, 5123–5138 (2021).
Mazurenko, S., Prokop, Z. & Damborsky, J. Machine learning in enzyme engineering. ACS Catal. 10, 1210–1223 (2019).
Chen, Y., Li, F., Mao, J., Chen, Y. & Nielsen, J. Yeast optimizes metal utilization based on metabolic network and enzyme kinetics. Proc. Natl. Acad. Sci. USA 118, e2020154118 (2021).
Kim, S. et al. PubChem 2019 update: improved access to chemical data. Nucleic Acids Res. 47, D1102–D1109 (2019).
Moretti, S., Tran, V. D. T., Mehl, F., Ibberson, M. & Pagni, M. MetaNetX/MNXref: unified namespace for metabolites and biochemical reactions in the context of metabolic models. Nucleic Acids Res. 49, D570–D574 (2021).
Adadi, R., Volkmer, B., Milo, R., Heinemann, M. & Shlomi, T. Prediction of microbial growth rate versus biomass yield by a metabolic network with kinetic parameters. PLoS Comput. Biol. 8, e1002575 (2012).
Chen, Y. et al. Proteome constraints reveal targets for improving microbial fitness in nutrient-rich environments. Mol. Syst. Biol. 17, e10093 (2021).
Elsemman, I. E. et al. Whole-cell modeling in yeast predicts compartment-specific proteome constraints that drive metabolic strategies. Nat. Commun. 13, 801 (2022).
Li, F. et al. Genome scale modeling of the protein secretory pathway reveals novel targets for improved recombinant protein production in yeast. Preprint at bioRxiv https://doi.org/10.1101/2021.10.16.464630 (2021).
Oftadeh, O. et al. A genome-scale metabolic model of Saccharomyces cerevisiae that integrates expression constraints and reaction thermodynamics. Nat. Commun. 12, 4790 (2021).
Lloyd, C. J. et al. COBRAme: a computational framework for genome-scale models of metabolism and gene expression. PLoS Comput. Biol. https://doi.org/10.1371/journal.pcbi.1006302 (2018).
Islam, M. M., Schroeder, W. L. & Saha, R. Kinetic modeling of metabolism: present and future. Curr. Opin. Syst. Biol. 26, 72–78 (2021).
Chen, F., Yuan, L., Ding, S., Tian, Y. & Hu, Q.-N. Data-driven rational biosynthesis design: from molecules to cell factories. Brief. Bioinform. 21, 1238–1248 (2020).
The UniProt Consortium. UniProt: the universal protein knowledgebase. Nucleic Acids Res. 45, D158–D169 (2017).
Tsubaki, M., Tomii, K. & Sese, J. Compound-protein interaction prediction with end-to-end learning of neural networks for graphs and sequences. Bioinformatics 35, 309–318 (2019).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Dong, Q.-W., Wang, X.-L. & Lin, L. Application of latent semantic analysis to protein remote homology detection. Bioinformatics 22, 285–290 (2006).
Kanehisa, M., Furumichi, M., Tanabe, M., Sato, Y. & Morishima, K. KEGG: new perspectives on genomes, pathways, diseases and drugs. Nucleic Acids Res. 45, D353–D361 (2017).
Shen, X.-X. et al. Tempo and mode of genome evolution in the budding yeast subphylum. Cell 175, 1533–1545 (2018).
Yang, Z. PAML 4: phylogenetic analysis by maximum likelihood. Mol. Biol. Evol. 24, 1586–1591 (2007).
Popovic, M. Thermodynamic properties of microorganisms: determination and analysis of enthalpy, entropy, and Gibbs free energy of biomass, cells and colonies of 32 microorganism species. Heliyon 5, e01950 (2019).
Heirendt, L. et al. Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v.3.0. Nat. Protoc. 14, 639–702 (2019).
Wang, H. et al. RAVEN 2.0: a versatile toolbox for metabolic network reconstruction and a case study on Streptomyces coelicolor. PLoS Comput. Biol. 14, e1006541 (2018).
Yu, R. et al. Nitrogen limitation reveals large reserves in metabolic and translational capacities of yeast. Nat. Commun. 11, 1881 (2020).
Acknowledgements
We acknowledge S. Viknander for giving feedback to improve this manuscript. This project received funding from the Novo Nordisk Foundation (grant no. NNF10CC1016517, J.N.), the Knut and Alice Wallenberg Foundation (J.N.) and the European Union’s Horizon 2020 research and innovation programme with projects DD-DeCaF (grant no. 686070, J.N., F.L., H.L. and Y.C.) and SynBio4Flav (grant no. 814650, E.J.K.). The computations were enabled by resources provided by the Swedish National Infrastructure for Computing at Chalmers Centre for Computational Science and Engineering and High Performance Computing Center North, partially funded by the Swedish Research Council through grant agreement no. 2018-05973 (F.L. and Y.C.).
Funding
Open access funding provided by Chalmers University of Technology.
Author information
Authors and Affiliations
Contributions
F.L., L.Y., H.L. and J.N. designed the research. F.L. and L.Y. performed the research. F.L., L.Y., Y.C., G.L., E.J.K. and J.N. analysed the data. L.Y. and M.K.M.E. collected the kcat data. F.L., L.Y., H.L, G.L., Y.C., M.K.M.E., E.J.K. and J.N. wrote the paper. All authors approved the final paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Catalysis thanks Dong-Yup Lee and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Figs. 1–13.
Supplementary Table
Supplementary Tables 1–8.
Supplementary Data
Source data for Supplementary Figs.
Source data
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Fig. 5
Statistical source data.
Source Data Fig. 6
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, F., Yuan, L., Lu, H. et al. Deep learning-based kcat prediction enables improved enzyme-constrained model reconstruction. Nat Catal 5, 662–672 (2022). https://doi.org/10.1038/s41929-022-00798-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41929-022-00798-z
This article is cited by
-
Reconstruction, simulation and analysis of enzyme-constrained metabolic models using GECKO Toolbox 3.0
Nature Protocols (2024)
-
Embracing data science in catalysis research
Nature Catalysis (2024)
-
Strategies to increase the robustness of microbial cell factories
Advanced Biotechnology (2024)
-
Genome-scale metabolic models reveal determinants of phenotypic differences in non-Saccharomyces yeasts
BMC Bioinformatics (2023)
-
UniKP: a unified framework for the prediction of enzyme kinetic parameters
Nature Communications (2023)