Introduction

There has been greater attention in the recent past about the application of supercritical carbon dioxide in micronization of pharmaceuticals1,2,3,4,5. The drug administration is decided by the size of the particle. As we know, intravenous drug delivery requires particles size ranging from 0.1 to 0.3 μm, inhalation delivery requires 1–5 μm and oral delivery requires 0.1–100 μm and the smaller the size of the particles, greater chance of a drug being absorbed by the human body, which helps in reducing the drug dosage1. Conventional particle reduction techniques result in products that are in the particulate range, for example jet mills provides product particles in the range 5–45 μm, hammer mill provides product particles in the range 25–600 μm, on the other hand supercritical fluids (SCFs) technology provides product particles in the range 0.1–600 μm1. But, to apply SCFs technology, solubility data of a specific drug in the desired SCF is required for the selection and design of suitable SCF process that reduces the particle size, thus the solubility will determine the operating condition of the process6,7,8. Present work is focused on the both solubility measurement and modelling of hydroxychloroquine sulfate (HCQS) in scCO2. This drug was originally developed in United States (US) to counter malaria in the year 19499,10. HCQS is considered as better alternate to chloroquine, due to less toxicity. It is also used for the treatment of Rheumatoid Arthritis (RA) and Systemic Lupus Erythematosus (SLE)9,11 disease. A recent study conducted by Pishnamazi et al., on the solubility of chloroquinein scCO2 has inspired us to take up this task12. Since 1950, chloroquine has been in use to treat malaria, however, hydroxychloroquine, a chloroquine analogue has a better safety profile due to a hydroxyl group on the side chain and is used in the treatment of connective tissue disorders13. We believe this study helps to implement SCF technology to get the desired drug size particles of HCQS and which may help to reduce the drug dosage in treatment. To expand the use of solubility data, modelling is performed with literature models and new solvate complex models.

This work is carried out in two steps. In the first, HCQS solubility in scCO2 solvent is determined and in the second, data measured in the first stage are correlated with literature models. The models employed are solid–liquid equilibrium, Chrastil, reformulated Chrastil, Méndez-Santiago and Teja (MST), Bartle et al., Reddy-Garlapati, Sodeifian et al., models and three forms of new solvate complex models.

Experimental

Materials

HCQS was supplied by TEMAD Co., Active Pharmaceuticals in gradients, Mashhad, Iran (CAS Number: 747-36-4, mass purity > 99%). CO2 (CAS Number: 124-38-9, mass purity > 99.9%) was purchased from Fadak company, Kashan, Iran. All the relevant details are tabulated in Table 1.

Table 1 Molecular structure and physicochemical properties of used materials.
Full size table

Solubility measurement details

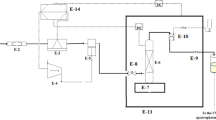
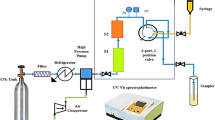
SCF-solubility of the drugs was experimentally measured via two broad classes of saturated solution-based methods, where solubility measurement can be done either (1) statically or (2) dynamically14. In the present work, a UV–vis spectrophotometer was utilized to statically examine the equilibrium solubility data of HCQS in a setup presented in Fig. 1. This experimental setup has already been validated in our previous work with alpha-tocopherol and naphthalene15. The solubilities were measured with the help of an equilibrium cell. Thermodynamically, the method employed may be regarded as an isobaric-isothermal method14. All the measurements are taken by keeping system temperatures and pressures at the desired value with high precision (i.e., ± 0.1 K and ± 0.1 MPa). Complete details about the equipment and measurement procedures are presented elsewhere15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35. However, the description of the equipment and the methodology employed in establishing solubility data are briefly presented in this section. The scCO2 is pumped to the equilibrium cell and drug sample and scCO2 are thoroughly mixed and allowed to attain equilibrium. It is observed that the equilibrium is attained in 60 min. To ensure equilibrium solubility, the experiments are performed with fresh samples at various time intervals. For a specified temperature and pressure in each experiment, the drug sample is contacted with scCO2 and stirred thoroughly in an equilibrium cell until a specific time (5 min, 10 min, 20 min, 30 min, 40 min, 50 min and 60 min) and the solubility readings are recorded. It is observed that the solubility is independent of time after 30 min. However, for solubility measurement, the samples are collected after 1 h. For each sampling a 600 µL volume saturated sample is collected via a collection valve in a deionized water preloaded sample vial. After discharging of each sample, the sampling valve was cleaned with 1 ml of deionized water. Drug sample solubility is estimated with the following formula:

$$y_2 = \frac{n_{drug} }{n_{drug} + n_{CO_2 } }$$
(1)

where \(y_{\scriptsize 2}\) is solubility of the drug in scCO2, \({n}_{\text{drug}}\) and \({n}_{{\text{CO}}_{2}}\) are number of moles of the drug and CO2 in the sampling loop, respectively.

Figure 1
figure 1

Experimental setup for solubility measurement, E1- CO2 cylinder; E2- Filter; E3- Refrigerator unit; E4- Air compressor; E5- High pressure pump; E6- Equilibrium cell; E7- Magnetic stirrer; E8- Needle valve; E9- Back-pressure valve; E10- Six-port, two position valve; E11- Oven; E12- Syringe; E13- Collection vial; and E14- Control panel.

Full size image

The following formulas are used in data conversion

$$n_{{{\text{drug}}}} = \frac{{C_{s} \cdot V_{s} }}{{M_{s} }}$$
(2)
$$n_{{CO_{2} }} = \frac{{V_{1} \rho_{1} }}{{M_{{CO_{2} }} }}$$
(3)

where \(C_{s}\) is concentration of the drug in g/L. V1 = 600 × 10–6 L and Vs = 5 × 10–3 L are sampling loop and vial volumes, respectively. \(M_{s}\) and \(M_{{CO_{2} }}\) are drug and CO2 molecular weights, respectively. ρ1 is density of scCO2 at each experimental condition, as presented in Table 2.

Table 2 Solubility of HCQC in scCO2 at various temperatures and pressures.
Full size table

Solubility is also described as

$$S = \frac{{C_{S} V_{s} }}{{V_{1} }}$$
(4)

The solubility and mole fraction relation is described as

$$S = \frac{{\rho M_{s}}}{{M_{{CO_{2}}}}}\frac{{y_{2}}}{{1 - y_{2}}}$$
(5)

The HCQS’s solubility is quantified in the UV–Visible spectrophotometer (Model UNICO-4802) with the help of deionized water \((conductivity \le 5\;\upmu {\text{S}}\;{\text{m}}^{ - 1} )\) as collection solvent with the wave length of 220 nm at UV spectrum.

Modelling

Although there are several approaches in modelling solubility data, solid–gas equilibrium (known as equation of state (EoS) approach), solid–liquid equilibrium (SLE, also known as expanded liquid equilibrium approach) and empirical modelling are commonly used in literature for the data correlation36,37,38,39,40,41,42,43,44,45,46,47,48,49,50. For EoS approach critical properties of both solvent (scCO2) and solute (HCQS) are required, whereas the SLE approach requires only melting temperature and melting enthalpy of the solute, but empirical modelling doesn’t need any such information. HCQS is a typical compound and it is not possible to estimate its critical properties due to the presence of H2SO4 in its structure. Due to this fact EoS modelling is not persuaded. On the other hand, experimental melting temperature and melting enthalpies of HCQS are available; due to this reason expanded liquid modelling is explored. For empirical modelling the density of scCO2, and system temperature and pressure are required; since they are readily available, it is also persuaded here. For empirical modelling, six commonly used solubility models are considered and those models have a varying number of parameters in their equations ranging from three to seven. The modelling purpose of some empirical models is to check the self-consistency of the measured data and to estimation some of the thermodynamic information of the dissolution process. In general, solubility of solids in SCFs is visualized in terms of solvate complex formation; therefore, a new set of solvate complex models is proposed for the better data fitting/correlation. More details about all the models considered in this work are presented in the following subsections.

Solid–liquid equilibrium (SLE) models

In this approach the HCQS solute is assumed to be infinitesimally dissolved in the scCO2 solvent. At equilibrium, the drug fugacity in solid phase is equal to that of fugacity of drug in scCO2 phase. From this criterion, the following solubility expression is proposed51,52,53,54,55,56,57.

$$y_{2} = \frac{1}{{\gamma_{2}^{\infty } }}\frac{{f_{2}^{S} }}{{f_{2}^{L} }}$$
(6)

From the literature, there are several models for this approach. However, Wilson activity coefficient model is considered for the data regression58.

We know from thermodynamics, \({\raise0.7ex\hbox{${f_{2}^{S} }$} \!\mathord{\left/ {\vphantom {{f_{2}^{S} } {f_{2}^{L} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${f_{2}^{L} }$}}\) ratio is

$$\frac{{f_{2}^{S} }}{{f_{2}^{L} }} = \exp \left[ {\frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right) - \int\limits_{{T_{m} }}^{T} {\frac{1}{{RT^{2} }}} \left[ {\int\limits_{{T_{m} }}^{T} {\left[ {\Delta C_{p} } \right]dT} } \right]dT} \right]$$
(7)

Simplified expression for \({\raise0.7ex\hbox{${f_{2}^{S} }$} \!\mathord{\left/ {\vphantom {{f_{2}^{S} } {f_{2}^{L} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${f_{2}^{L} }$}}\) is27

$$\ln \left( {\frac{{f_{2}^{S} }}{{f_{2}^{L} }}} \right) = \frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right)$$
(8)

The required \(\gamma_{2}^{\infty }\) is obtained from Wilson model and the relevant expressions are as follows:

$$ln\left( {\gamma_{2}^{\infty } } \right) = 1 - \Lambda_{12} - ln\left( {\Lambda_{21} } \right)$$
(9)

where

$$\Lambda_{12} = \frac{{v_{2} }}{{v_{1} }}{\text{exp}}\left( { - \frac{{\lambda_{12} }}{RT}} \right)$$
(10)
$$\Lambda_{21} = \frac{{v_{1} }}{{v_{2} }}{\text{exp}}\left( { - \frac{{\lambda_{21} }}{RT}} \right)$$
(11)
$$\Lambda_{12} = v_{2} \rho_{c1} \rho_{r} exp\left( { - \frac{{\lambda_{12}^{^{\prime}} }}{{T_{r} }}} \right)$$
(12)
$$\Lambda_{12} = \frac{1}{{v_{2} \rho_{c1} \rho_{r} }}exp\left( { - \frac{{\lambda_{21}^{^{\prime}} }}{{T_{r} }}} \right)$$
(13)
$$\lambda_{12}^{^{\prime}} = \frac{{\lambda_{12} }}{{RT_{c1} }} \,{\text{and}}\,\lambda_{21}^{^{\prime}} = \frac{{\lambda_{21} }}{{RT_{c1} }}$$
$$lnv_{2} \left( {{\text{m}}^{3} \;{\text{mol}}^{ - 1} } \right) = \alpha_{2} ln\rho_{1} ({\text{kg}}\;{\text{m}}^{ - 3} ) + \beta_{2}$$
(14)
$$v_{2} = \alpha \rho_{r} + \beta$$
(15)

On combining Eqs. (10)–(15), we get

$$\Lambda_{12} = \left( {\alpha \rho_{r} + \beta } \right)\rho_{c1} \rho_{r} exp\left( { - \frac{{\lambda_{12}^{^{\prime}} }}{{T_{r} }}} \right)$$
(16)
$$\Lambda_{21} = \frac{1}{{ \left( {\alpha \rho_{r} + \beta } \right)\rho_{c1} \rho_{r} }}exp\left( { - \frac{{\lambda_{21}^{^{\prime}} }}{{T_{r} }}} \right)$$
(17)

\(\lambda_{21}^{^{\prime}}\) and \(\lambda_{12}^{^{\prime}}\) are the energies of interactions, where subscripts 1 and 2 denote solvent and solute, respectively.

Combining all the equations, finally, resulted in SLE model, i.e., Eq. (18)

$$y_{2} = {{\exp \left( {\frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right)} \right)} \mathord{\left/ {\vphantom {{\exp \left( {\frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right)} \right)} {\exp \left( {1 - \left( {\alpha \rho_{r} + \beta } \right)\rho_{c1} \rho_{r} \exp \left( { - \frac{{\lambda^{\prime}_{12} }}{{T_{r} }}} \right) - \ln \left( {\frac{1}{{\left( {\alpha \rho_{r} + \beta } \right)\rho_{c1} \rho_{r} }}\exp \left( { - \frac{{\lambda^{\prime}_{21} }}{{T_{r} }}} \right)} \right)} \right)}}} \right. \kern-0pt} {\exp \left( {1 - \left( {\alpha \rho_{r} + \beta } \right)\rho_{c1} \rho_{r} \exp \left( { - \frac{{\lambda^{\prime}_{12} }}{{T_{r} }}} \right) - \ln \left( {\frac{1}{{\left( {\alpha \rho_{r} + \beta } \right)\rho_{c1} \rho_{r} }}\exp \left( { - \frac{{\lambda^{\prime}_{21} }}{{T_{r} }}} \right)} \right)} \right)}}$$
(18)

Commonly used empirical models

Chrastil's model59

In the year 1981, Josef Chrastil presented a model for the solubility of solids/liquids in SCF. The main basis of the model is a solvate complex formulation based on a simple reaction. According to Chrastil, solubility is explained by \(c_{2} = c_{2} (\kappa ,\rho_{1} ,T)\), where \(\kappa\) is association number, \(\rho_{1}\) is solvent density (scCO2) and T is temperature. Chrastil proposed Eq. (19)

$$c_{2} = \rho_{1}^{\kappa } \exp \left( {A_{1} + \frac{{B_{1} }}{T}} \right)$$
(19)

An alternative from of Eq. (19) is Eq. (20)60

$$y_{2} = \frac{{\left( {\rho_{1} } \right)^{\kappa - 1} \exp \left( {A_{1} + \frac{{B_{1} }}{T}} \right)}}{{\left[ {1 + \left( {\rho_{1} } \right)^{\kappa - 1} \exp \left( {A_{1} + \frac{{B_{1} }}{T}} \right)} \right]}}$$
(20)

where y2 is solute solubility in mole fraction.

Reformulated Chrastil's model61

In the year 2009, Garlpati and Madras has reformulated Chrastil's model and it is expressed by Eq. (21), where solubility is explained by \(y_{2} = y_{2} \left( {\kappa^{\prime},\rho_{1} ,T} \right)\), in which \(\kappa^{\prime}\) is association number, \(\rho_{1}\) is solvent density (scCO2) and T is temperature.

$$y_{2} = \left( {\frac{{RT\rho_{1} }}{{M_{ScF} f^{ \bullet } }}} \right)^{{\kappa^{\prime} - 1}} \exp \left( {A_{2} + \frac{{B_{2} }}{T}} \right)$$
(21)

in Eq. (21), R denotes universal constant of ideal gas, \(M_{ScF}\) is molecular weight of solvent, \(f^{ * }\) is reference pressure and \(A_{2} \;\) and \(\;B_{2}\) are the Reformulated model constants.

Méndez-Santiago and Teja (MST) model62

The MST model is used to check the consistency of the data. All the data falls around a single straight line when \(T\ln \left( {y_{2} P} \right) - C_{3} T\) versus \(\rho_{1}\) is established. MST model is expressed as Eq. (22)

$$T\ln \left( {y_{2} P} \right) = A_{3} + B_{3} \rho_{1} + C_{3} T$$
(22)

where A3 to C3 are the model constants.

Bartle et al., model63

The solute sublimation enthalpy is calculated with Bartle et al., model and it is stated as

$$\ln \left( {\frac{{y_{2} P}}{{P_{ref} }}} \right) = A_{4} + \frac{{B_{4} }}{T} + C_{4} \left( {\rho_{1} - \rho_{ref} } \right)$$
(23)

where A4 to C4 are the model constants. Using the constant \(B_{4}\), sublimation enthalpy is calculated (i.e., \(\Delta_{sub} H = - B_{4} R\)).

Reddy-Garlapati model64

It is the model developed based on the degree of freedom analysis based on drug compounds. According to this model, solubility, \(y_{2} = y_{2} \left( {T_{r} ,P_{r} } \right)\), is expressed as Eq. (24), where \(T_{r}\) and \(P_{r}\) are reduced temperature and pressures, respectively.

$$y_{2} = \left( {A_{5} + B_{5} P_{r} + C_{5} P_{r}^{2} } \right)T_{r} + (D_{5} + E_{5} P_{r} + F_{5} P_{r}^{2} )$$
(24)

where \(A_{5}\) to \(F_{5}\) are the model constants.

Sodeifian et al., model65

It is another recently proposed empirical model. According to this model, solubility,\(y_{2} = y_{2} \left( {T,P,\rho_{1} } \right)\), can be calculated by

$$y_{2} = A_{6} + B_{6} \frac{{P^{2} }}{T} + C_{6} \ln \left( {\rho_{1} T} \right) + D_{6} \rho_{1} \ln \left( {\rho_{1} } \right) + E_{6} P\ln \left( T \right) + F_{6} \frac{{\ln \left( {\rho_{1} } \right)}}{T}$$
(25)

where \(A_{6}\) to \(F_{6}\) are the model constants.

New solvate complex models66

The solubility is visualized via solvate complex formation. The following simple reversible reaction is considered for the formation of solvate complex \(AB_{\kappa }\), in which ‘A’ is designated as solute and the letter ‘B’ is designated as solvent in SCF mixture.

$$A + \kappa^{\prime\prime}B \Leftrightarrow AB_{\kappa }$$
(26)

At equilibrium

$$K_{f} = \frac{{\left( {{{\hat{f}_{{AB_{\kappa } }} } \mathord{\left/ {\vphantom {{\hat{f}_{{AB_{\kappa } }} } {f_{{AB_{\kappa } }}^{ * } }}} \right. \kern-0pt} {f_{{AB_{\kappa } }}^{ * } }}} \right)_{SP} }}{{\left( {{{\hat{f}_{A} } \mathord{\left/ {\vphantom {{\hat{f}_{A} } {f_{A}^{ * } }}} \right. \kern-0pt} {f_{A}^{ * } }}} \right)_{Solid} \;\left( {{{\hat{f}_{B} } \mathord{\left/ {\vphantom {{\hat{f}_{B} } {f_{B}^{ * } }}} \right. \kern-0pt} {f_{B}^{ * } }}} \right)^{\kappa }_{SP} }}$$
(27)

where the subscript ‘Solid’ is designated as solid phase and subscript ‘SP’ is designated as solvent phase and superscript ‘\(*\)’ is reference state.

For each species the fugacity’s expressions are

$$\hat{f}_{A} = y_{A} \hat{\phi }_{A} P$$
(28)
$$\hat{f}_{B} = y_{B} \hat{\phi }_{B} P$$
(29)
$$\hat{f}_{{AB_{\kappa } }} = y_{{AB_{\kappa } }} \hat{\phi }_{{AB_{\kappa } }} P$$
(30)
$$f_{{AB_{\kappa } }}^{ * } = \phi_{{AB_{\kappa } }}^{ * } \;P^{ * }$$
(31)
$$f_{A}^{ * } = \phi_{A}^{ * } \;P^{ * }$$
(32)
$$f_{B}^{ * } = \phi_{B}^{ * } \;P^{ * }$$
(33)

At equilibrium in vapour phase only two things exit: one is solvent and the other is solvate complex thus

$$y_{B} + y_{ {AB_{\kappa } }} = 1$$
(34)

where \(y_{B} , y_{{AB_{\kappa } }}\) are respective mole fractions.

If we assume the standard state of species ‘A’ is pure under same system conditions. Then

$$\hat{f}_{A} = f_{A}$$
(35)

Fugacity of species ‘A’ can be written as

$$f_{A} = P_{A}^{Sub} \exp \left[ {\frac{{v_{A} \left( {P - P_{A}^{Sub} } \right)}}{RT}} \right]$$
(36)

From thermodynamics, equilibrium constant is function of salvation enthalpy as Eq. (37)

$$\ln \left( {K_{f} } \right) = {{\Delta H_{S} } \mathord{\left/ {\vphantom {{\Delta H_{S} } {RT + q_{s} }}} \right. \kern-0pt} {RT + q_{s} }}$$
(37)

Sublimation pressure can be expressed as Eq. (38)

$$\ln \left( {P_{A}^{Sub} } \right) = \alpha^{\prime} - {{\beta^{\prime}} \mathord{\left/ {\vphantom {{\beta^{\prime}} T}} \right. \kern-0pt} T}$$
(38)

Substituting Eqs. (35)–(38) into Eq. (27) along with two simplifications gives Eq. (39)

One assumption that \({{v_{A} P} \mathord{\left/ {\vphantom {{v_{A} P} {RT}}} \right. \kern-0pt} {RT}}\) is expressed as \({{Zv_{A} \rho_{1} } \mathord{\left/ {\vphantom {{Zv_{A} \rho_{1} } M}} \right. \kern-0pt} M}\) where \(\rho_{1}\) is the density of the supercritical phase and the second assumption is refereed to negligible term \({{v_{A} P_{A}^{Sub} } \mathord{\left/ {\vphantom {{v_{A} P_{A}^{Sub} } {RT}}} \right. \kern-0pt} {RT}}\)(~ 10–8–10–9) [since the sublimation pressures are very low and their order is about (~ 10–3–10–4) and the drug molar volume is also about the order (~ 10–4)]67,68,69,70.

$$\ln \left( {y_{{AB_{\kappa } }} } \right) - \kappa \ln \left( {y_{B} } \right) + \left( {1 - \kappa^{\prime\prime}} \right)\ln \left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right) = {L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N$$
(39)

where \(L = \left( {{{\Delta H_{s} } \mathord{\left/ {\vphantom {{\Delta H_{s} } R}} \right. \kern-0pt} R} - \beta^{\prime}} \right)\), \(M = \left( { - {{ZV_{A} } \mathord{\left/ {\vphantom {{ZV_{A} } M}} \right. \kern-0pt} M}} \right)\) and \(N = \ln \left( {\frac{{\left( {\varphi_{A}^{ * } } \right)\left( {{{\hat{\varphi }_{{AB_{\kappa } }} } \mathord{\left/ {\vphantom {{\hat{\varphi }_{{AB_{\kappa } }} } {\varphi_{{AB_{\kappa } }}^{ * } }}} \right. \kern-0pt} {\varphi_{{AB_{\kappa } }}^{ * } }}} \right)}}{{\left( {{{\hat{\varphi }_{B} } \mathord{\left/ {\vphantom {{\hat{\varphi }_{B} } {\varphi_{B}^{ * } }}} \right. \kern-0pt} {\varphi_{B}^{ * } }}} \right)^{\kappa } }}} \right) + \ln P^{ * } + q_{s} - \alpha^{\prime}\)

Equation (39) is rearranged as Eq. (40)

$$y_{{AB_{\kappa } }} = \left( {y_{B} } \right)^{{\kappa^{\prime\prime}}} \left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{\left( {\rlap{--} \kappa^{\prime\prime} - 1} \right)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)$$
(40)

Further, on rearranging Eq. (40), we get Eq. (41)

$${{y_{{AB_{\kappa } }} } \mathord{\left/ {\vphantom {{y_{{AB_{\kappa } }} } {\left( {1 - y_{{AB_{\kappa } }} } \right)^{{\kappa^{\prime\prime}}} }}} \right. \kern-0pt} {\left( {1 - y_{{AB_{\kappa } }} } \right)^{{\kappa^{\prime\prime}}} }} = \left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{\left( {\kappa^{\prime\prime} - 1} \right)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)$$
(41)

Applying binomial expansion to the left side term gives Eq. (41)

$${{y_{{AB_{\kappa } }} } \mathord{\left/ {\vphantom {{y_{{AB_{\kappa } }} } {\left( {1 - \kappa^{\prime\prime}\;y_{{AB_{\kappa } }} } \right)}}} \right. \kern-0pt} {\left( {1 - \kappa^{\prime\prime}\;y_{{AB_{\kappa } }} } \right)}} = \left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{\left( {\kappa^{\prime\prime\prime} - 1} \right)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)$$
(42)

We know solubility, \(y_{2}\), is related to cluster mole fraction \(y_{{AB_{\kappa } }}\) as Eq. (43)68,69

$$y_{2} = {{y_{{AB_{\kappa } }} } \mathord{\left/ {\vphantom {{y_{{AB_{\kappa } }} } {(1 + \kappa^{\prime\prime}\;y_{{AB_{\kappa } }} )}}} \right. \kern-0pt} {(1 + \kappa^{\prime\prime}\;y_{{AB_{\kappa } }} )}}$$
(43)

Thus the solubility is expressed as Eq. (44)

$$y_{2} = {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \mathord{\left/ {\vphantom {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} {\left[ {1 + \kappa^{\prime\prime}\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}} \right. \kern-0pt} {\left[ {1 + \kappa^{\prime\prime}\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}$$
(44)

\(\kappa^{\prime\prime}\) is a function of reduced density, given by Eq. (45)71

$$\kappa^{\prime\prime} = a_{1} + a_{2} \rho_{r} + a_{3} \rho_{r}^{2}$$
(45)

Combining Eqs. (44) and (45) results in Eq. (46)

$$y_{2} = {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} + a_{3} \rho_{r}^{2} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \mathord{\left/ {\vphantom {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} + a_{3} \rho_{r}^{2} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} {\left[ {1 + \left( {a_{1} + a_{2} \rho_{r} + a_{3} \rho_{r}^{2} } \right)\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} + a_{3} \rho_{r}^{2} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}} \right. \kern-0pt} {\left[ {1 + \left( {a_{1} + a_{2} \rho_{r} + a_{3} \rho_{r}^{2} } \right)\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} + a_{3} \rho_{r}^{2} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}$$
(46)

To reduce the number constants in Eq. (46), we have a choice to choose \(\kappa\) as a linear function of reduced density or as constant. Thus, we get the following two reduced solubility expressions.

$$y_{2} = {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \mathord{\left/ {\vphantom {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} {\left[ {1 + \left( {a_{1} + a_{2} \rho_{r} } \right)\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}} \right. \kern-0pt} {\left[ {1 + \left( {a_{1} + a_{2} \rho_{r} } \right)\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(a_{1} + a_{2} \rho_{r} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}$$
(47)

and

$$y_{2} = {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \mathord{\left/ {\vphantom {{\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} {\left[ {1 + \left( {\kappa^{\prime\prime}} \right)\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}} \right. \kern-0pt} {\left[ {1 + \left( {\kappa^{\prime\prime}} \right)\left[ {\left( {{P \mathord{\left/ {\vphantom {P {P^{ * } }}} \right. \kern-0pt} {P^{ * } }}} \right)^{{(\kappa^{\prime\prime} - 1)}} \exp \left( {{L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T} + M\rho + N} \right)} \right]} \right]}}$$
(48)

In literature, related solubility expression is proposed by Rajasekhar and Madras67 as

$$y_{2} = \left( {\frac{P}{{P^{ * } }}} \right)^{\begin{subarray}{l} \left( {\kappa^{\prime\prime\prime} - 1} \right) \\ \end{subarray} } \exp \left( {{{L^{\prime}} \mathord{\left/ {\vphantom {{L^{\prime}} {T + M^{\prime}\rho + N^{\prime}}}} \right. \kern-0pt} {T + M^{\prime}\rho + N^{\prime}}}} \right)$$
(49)

The correlating abilities and evaluation of the new models (Eqs. 46–48) and existing model (Eq. 49) are also carried out in this work.

The data fitting to the models are performed by an objective function Eq. (50)72

$$OF = \sum\limits_{i = 1}^{N} {\frac{{\left| {y_{2i}^{\exp } - y_{2i}^{calc} } \right|}}{{y_{2i}^{\exp } }}}$$
(50)

The obtained deviations are indicated in terms of an average absolute relative deviation percentage (AARD%).

$${\text{AARD}}\% = \left( {{\raise0.7ex\hbox{${100}$} \!\mathord{\left/ {\vphantom {{100} {N_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${N_{i} }$}}} \right)\sum\limits_{i = 1}^{N} {\frac{{\left| {y_{2i}^{\exp } - y_{2i}^{cal} } \right|}}{{y_{2i}^{\exp } }}}$$
(51)

The entire regression task was done using (MATLAB 2019a®) version software, also this can be performed by nonlinear regression methods with the same results84,85.

Results and discussion

The experimental device used for the measurement of HCQS solubility in scCO2 is accurate and reliable. It was successfully tested to reproduce the solubilities of naphthalene in scCO2 and alpha-tocopherol in scCO2 systems and the same was reported in our earlier work15. The solubility values reported for alpha-tocopherol in our previous work, are the average of three replicate measurements with relative standard deviations lower than 5.7%15. The solubility values of naphthalene reported in our previous work are also the average of three replicate measurements with relative standard deviations lower than 6.5%15. Table 2 shows the measured solubilities of HCQS in scCO2 at various conditions and the density of the scCO2, obtained from the NIST data base73. From solubility data, it is clear that present system (HCQS+scCO2), does not exhibit the usual retrograde phenomenon. Affecting solvent density and solute power, the temperature was found to impose a dual impact on solubility in scCO2 depending on how the solute vapor pressure and solvent density are balanced. In this respect, increasing the solution temperature may enhance the solute vapor pressure, thereby contributing to stronger solvating power of SCF. At the same time, a rise of temperature may lower the scCO2 density which is known to depreciate the overall solvating power of the fluid. The mole fraction versus pressure isotherms on Fig. 2 suggest an enhancement in the solubility of drug upon elevating the temperature. This proves the dominant role of the solute vapor pressure in determining the solubility behavior irrespective of the pressure. Reports by other researchers confirm the results of the present work regarding the effect of temperature on the solubility in scCO274,75,76. From Table 2 and Fig. 2, it is clear that when temperature is raised from 308 to 338 K, there is a clear indication of a rise in solubility from 0.0304 × 10−4 to 0.1398 × 10−4 at 12 MPa (i.e., 4.6 folds’ increase) and at 27 MPa from 0.1459 × 10−4 to 0.5515 × 10−4 (i.e., 3.8 folds increase). At the same time, at 12 MPa, the density of scCO2 changes from 769 to 338 kg m−3 at 308 and 338 K, respectively. Similarly, the density of scCO2 at 27 MPa changes from 914 to 783 kg m−3 at 308 and 338 K, respectively; which means that there is decrease in density at 12 MPa (low pressure) (i.e., 338/769 = 0.4395) and there is increase in density to some extent at 27 MPa (higher pressure) (i.e., 783/914 = 0.8567). Thus, the solubility behavior of HCQS in scCO2 is highly nonlinear. This kind of high nonlinearity behavior has been observed with amlodipine besylate-scCO2 in the recent past28. This kind of high nonlinearity behavior can’t be captured with simple models. Thus models having more adjustable constants are required to fit the data and this would augment the justification for the need of development of new models.

Figure 2
figure 2

Solubility isotherms of HCQS in scCO2.

Full size image

All the regression results are summarized in Table 3 and presented in Figs. 3, 4, 5, 6, 7, 8 and 9. Solid–liquid model requires enthalpy of fusion, molar volume and melting point of the solute. Enthalpy of fusion is estimated with the help Jain et al.77, and molar volume of the solute is estimated with the help Immirzi and Perini method78. The calculated molar enthalpy and molar volumes are 65,208 J mol−1 and 3.306 × 10–4 m3 mol−1, respectively. The melting temperature is obtained from the material safety data sheet as 240 °C. From Chrastil's model constant (\(B_{1}\)), total enthalpy is calculated (\(B_{1}\) × R). From Bartle’s model constant (\(B_{4}\)), sublimation enthalpy is calculated (\(\Delta_{sub} H = - B_{4} R\)). From the magnitude difference between total and sublimation enthalpies, solvation enthalpy is calculated. Similarly, from reformulated Chrastil's model constant (\(B_{2}\)) and Bartle’s model constant (\(B_{4}\)), combination solvation enthalpy is calculated. All the calculated quantities are shown in Table 4. The regression ability of commonly used three parameter models are found to be inferior when compared to Sodeifian et al., and Reddy–Garlapati models. This may be due to a smaller number of parameters in the models; on the other hand, the correlating ability of the solvate complex models is quite good. However, among all empirical models, Reddy-Garlapati model is the best model. The newly proposed solvate complex models have more adjustable constants, and thus their predictions are also good. From the solvate complex model’s constants, it is interesting to note the behavior of association number. When association number is treated as a linear function of reduced density, the obtained average association number for the solubility data is \(\kappa^{\prime\prime}_{ave}\) = 2.21, which is lesser than that of the conventional Chrastil's model \(\kappa\) = 3.89. But, when association number is treated as quadratic function of reduced density, the obtained average association number for the solubility data is \(\kappa^{\prime\prime}_{ave}\) = 3.78, and it is matching well with association number of Chrastil’s model. From those results and from literature arguments, we can infer that association number is quadratic function of \(\rho_{r}\) so that is apparent than other forms and its correlations are reliable71,79. Thus, association number as quadratic function of \(\rho_{r}\) is recommended for the data interpolation.

Table 3 Regression results of all models used in this research.
Full size table
Figure 3
figure 3

HCQS solubility in scCO2 versus ρ1. Symbols are experimental data points. Solid lines are calculated from SLE model (Eq. 18).

Full size image
Figure 4
figure 4

HCQS solubility in scCO2 versus ρ1. Symbols are experimental data points. Solid lines are calculated from Chrastil's model (Eq. 20).

Full size image
Figure 5
figure 5

HCQS solubility in scCO2 versus ρ1. Symbols are experimental data points. Solid lines are calculated from SLE model (Eq. 21).

Full size image
Figure 6
figure 6

Self-consistency plot based on MST model (Eq. 22).

Full size image
Figure 7
figure 7

ln(y2 P/Pref) versus (ρ1 − ρref). Symbols are experimental data points. Solid lines are calculated from Bartle et al., model (Eq. 23).

Full size image
Figure 8
figure 8

HCQS solubility in scCO2 versus ρ1.Symbols are experimental data points. Solid lines and broken linesare calculated from Reddy-Garlapati and Sodeifian models (Eqs. 24, 25), respectively.

Full size image
Figure 9
figure 9

HCQS solubility in scCO2 versus \(\rho_{1}\). Symbols and lines are experimental and calculated from new solvate complex models (Eqs. 46, 47, 48), respectively.

Full size image
Table 4 Enthalpies of sublimation and solvation of HCQS.
Full size table

Further, a comparative analysis is done to determine the best model for HCQS-scCO2 system. Since, a varying number of parameters are involved in the equations considered in the work, Akaike Information Criterion (AIC) and corrected AIC (AICc)80,81,82,83 are used to identify the best model. AIC alone is used when data points are more than forty; on the other hand, AICc is used when data points are less than forty. In the present there are only twenty-four solubility data points in our hands; hence, AICc is used for identifying the best model. AICc is defined as Eq. (52)

$$AIC_{c} = AIC + \frac{{2Q\left( {Q + 1} \right)}}{N - Q - 1}$$
(52)

where N is solubility data points, Q is number of model constants, and SSE is error sum of squares. From the least AICc value, the best model is identified. The lower the AICc value the greater the accuracy of the model, and it is independent of the number of parameter. All the AICc values are reported in Table 5. From results, Reddy-Garlapati and the new solvate complex models are observed to be the better models.

Table 5 Summary of SSE, RMSE, AIC and AICc of all solubility models.
Full size table

Conclusion

Solubilities of solid HCQS in scCO2 solvent were measured at various conditions ranging from P = 12 to 27 MPa and T = 308 to 338 K. The measured data’s range is from 0.0304 × 10–4 to 0.5515 × 10−4 in terms of mole fraction. Three forms of solvate complex models explored in this study are reasonable in estimating solubility and among the three the best model is observed to have AICc and AARD values − 595.4 and 10.08% respectively. Among empirical models Reddy-Garlapati model is observed to fit the data quite well and with the corresponding AICc and AARD values − 604.1 and 10.04%, respectively.