Experimental solubility and modeling of Crizotinib (anti-cancer medication) in supercritical carbon dioxide

Abstract

Measurement of saturation solubility of drugs in a supercritical fluid is an important parameter for the implementation of supercritical technology in pharmaceutical industry. CO₂ is the most sorted substance as a supercritical fluid since it has attractive properties like easily achievable critical temperature, moderate pressure. Cancer is increasingly affecting the mankind, a proper dosage while treating would help in minimizing the drug usage. The bioavailability of the drug is mainly influenced by the drug particle size. An appropriate technology is always useful in making suitable drug particles; thus, supercritical fluid technology (SFT) is considered as promising technique for the production of micro and nanoparticles. Since, particle production process through SFT needs solubility information, appropriate solubility information is necessary. In the present work, Crizotinib (anti-cancer drug) solubility in supercritical carbon dioxide (scCO₂) is measured and reported, for the first time. The obtained solubilities are at temperatures 308, 318, 328,338 K and pressures 12, 15, 18, 21, 24 to 27 MPa. The measured solubilities are ranged in terms of mole fraction from (0.483 × 10⁻⁵ to 0.791 × 10⁻⁵) at 308 K, (0.315 × 10⁻⁵ to 0.958 × 10⁻⁵) at 318 K, (0.26 × 10⁻⁵ to 1.057 × 10⁻⁵) at 328 K, (0.156 × 10⁻⁵ to 1.219 × 10⁻⁵) at 338 K. The cross over region is observed at 14.5 MPa. To expand the application of the solubility data, few important solubility models and three cubic equations of sate (cubic EoS) models along with Kwak and Mansoori mixing rules are investigated. Sublimation and salvation enthalpies of Crizotinib dissolution in scCO₂ are calculated.

Introduction

Traditionally, pharmaceutical particle production processes use several organic solvents for processing their products. Quite often, remnant of solvents causes serious pollution and sometimes reactions with pharmaceutical products and result in unnecessary byproducts. These issues are effectively handled using supercritical fluid technologies (SFTs). Although, there is a scope of using several substances as supercritical fluids, CO₂ as supercritical fluid has gained importance for the last three decades. Commonly, all supercritical fluids (SCFs) have gas like diffusivities and liquid like densities makes them attractive for extraction processes. When CO₂ pressure and temperature conditions are maintained above 7.39 MPa and 304.15 K, it will act as supercritical fluid and it is commonly abbreviated as supercritical carbon dioxide (scCO₂)^1,2,3,4. Due to these features, it is used as a solvent in various process applications^{1,2,3,4,5,6,7,8}.Some of the major applications of scCO₂ in process industry are pharmaceutical particle size design, food processing, textile dyeing and extraction^1,2,3,4.Solubility information is necessary for the proper implementation of SFTs for particle size design process. The task of measuring solubility of important anti-cancer drugs in scCO₂ is taken in this work. In recent literature, solubilities of several anti-cancer drugs in scCO₂ are readily available^{8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26}, but the Crizotinib solubility in scCO₂ is not reported, therefore in this work for the first time its solubility is measured and reported. Crizotinib is used in the treatment of some kind of non-small cell lung cancer (NSCLC) that spreads to nearby tissues or to other parts of the body²⁷.Crizotinib helps to stop the growth of tumor cells by blocking the anaplastic lymphoma kinase (ALK) protein from working; it is also termed as fusion mutation. Appropriate dosage is attained with proper drug particle size and it is very critical for the treatment of cancer. Thus, the information obtained this study is useful in preparing various size drug particles using scCO₂. For practical purpose obtaining solubilities at various conditions are cumbersome hence model identification for the solubility is essential²⁸. The data developed in this work are tested with few important solubility models and three cubic equation of state models (cubic EoS) along with Kwak and Mansoori mixing rules²⁹.

The purpose of this study is in two levels. In the first level, Crizotinib solubility in scCO₂ is determined and in the second, data obtained are correlated with existing solubility models and with three Cubic EoS models along with Kwak and Mansoori mixing rules.

Experimental

Materials

Crizotinib is supplied by Amin Pharma company (CAS Number: 877399-52-5, mass purity > 99%). CO₂ (CAS Number: 124-38-9, mass purity > 99.9%) is purchased from Fadak company, Kashan (Iran). Dimethyl sulfoxide (DMSO, CAS Number: 67-68-5, mass purity > 99%) is procured from Sigma Aldrich company. Table 1 indicates the information about the chemicals utilized in this work.

Table 1 Molecular structure and physicochemical properties of used materials.

Experiment details

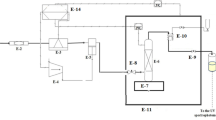
The experimental setup utilized in this study is shown in Fig. 1. The details about the solubility apparatus and experimental procedure are presented in our earlier studies (Fig. 1)^{30,31,32,33,34,35,36,37,38,39,40,41,42}. However, a brief description is presented in this section. The method of solubility measurement utilized is classified as an isobaric-isothermal method⁴³. All measurements were made with high precision while controlling temperatures and pressures within ± 0.1 K and ± 0.1 MPa, respectively. Solubility measurements were performed at least in triplicate for each data point. For each measurement, 1 g of Crizotinib drug was used. In line with our previous works, for this compound, the observed equilibrium was within 60 min. After equilibrium, 600 µL saturated scCO₂ sample was collected via 2-status 6-way port valve in a DMSO preloaded vial. After discharging 600 µL saturated scCO₂, the port valve was washed with 1 ml DMSO. Thus, the total saturation solution was 5 ml. Drug solubility in terms of mole fraction is calculated with the following formula:

$$y_{2} = \frac{{n_{drug} }}{{n_{drug} + n_{{CO_{2} }} }}$$

(1)

where $n_{{{\text{drug}}}}$ is number of moles of the drug, and $n_{{{\text{CO}}_{{2}} }}$ is number of moles of CO₂ in the sampling loop.

Figure 1

Experimental setup for solubility measurement, E1—CO₂ cylinder; E-2—Filter; E-3—Refrigerator unit; E-4—Air compressor; E-5—High pressure pump; E-6—Equilibrium cell; E-7—Magnetic stirrer; E-8—Needle valve; E-9—Back-pressure valve; E-10 Six-port, two position valve; E-11—Oven; E-12—Syringe; E13—Collection vial; E-14—Control panel.

Furthermore, the above quantities are given as:

$$n_{{{\text{drug}}}} = \frac{{C_{s} \cdot V_{s} }}{{M_{s} }}$$

(2)

$$n_{{{\text{CO}}_{{2}} }} = \frac{{V_{1} \cdot \rho }}{{M_{{{\text{CO}}_{{2}} }} }}$$

(3)

where $C_{{\text{s}}}$ is the drug concentration in saturated sample vial in g/L. The volume of the sampling loop and vial collection are V₁(L) = 600 $\times$ 10⁻⁶ m³ and V_s(L) = 5 $\times$ 10⁻³ m³, respectively. The $M_{s}$ and $M_{{CO_{2} }}$ are the molecular weights of the drug and CO₂, respectively. Solubility is also described as

$$S = \frac{{C_{S} V_{s} }}{{V_{1} }}$$

(4)

The relation between S and $y_{2}$ is

$$S = \frac{{\rho M_{s} }}{{M_{{CO_{2} }} }}\frac{{y_{2} }}{{1 - y_{2} }}$$

(5)

The Crizotinib’s solubility was determined using a UV–Visible spectrophotometer (Model UNICO-4802) and DMSO solvent was used for the measurement of its solubility. Drug samples were analyzed at wave length of 270 nm.

Modeling

The Crizotinib’s solubility data measured in this study is correlated by four standard solubility models namely Chrastil, Modefied Chrastil, Mendez-Santiago and Teja and Bartle et al. Moreover, three cubic EoS models along with Kwak and Mansoori mixing rules are explored for the solubility data correlation. More details about the models considered in this work are presented in the following subsections⁶.

Standard solubility models

Chrastil model⁴⁴

Chrastil model represents by Eq. (6) that relates solubility mole fraction in terms of solvent density, association number and temperature

$$c_{2} = \rho_{1}^{\kappa } \exp \left( {A_{1} + \frac{{B_{1} }}{T}} \right)$$

(6)

where model constants are $\kappa ,A_{1} \;{\text{and}}\;B_{1}$.

Equation (6) is alternatively represented as⁴⁵

$$y_{2} = \frac{{\left( {\rho_{1} } \right)^{\kappa - 1} \exp \left( {A_{1} + \frac{{B_{1} }}{T}} \right)}}{{\left[ {1 + \left( {\rho_{1} } \right)^{\kappa - 1} \exp \left( {A_{1} + \frac{{B_{1} }}{T}} \right)} \right]}}$$

(7)

where $\kappa ,A_{1} \;{\text{and}}\;B_{1}$ are the model parameters.

Modified Chrastil model⁴⁶

Dimensionally corrected Charstil model is also known as modified Charstil model and is described in terms of solvent density, association number and temperature as

$$y_{2} = \left( {\frac{{RT\rho_{1} }}{{M_{ScF} f^{ \bullet } }}} \right)^{{\kappa^{\prime} - 1}} \exp \left( {A_{2} + \frac{{B_{2} }}{T}} \right)$$

(8)

where $\kappa^{\prime},A_{2} \;{\text{and}}\;B_{2}$ are the model parameters.

Méndez-Santiago and Teja (MT) model⁴⁷

Measured data self-consistency is checked with this model and represents by Eq. (9)

$$T\ln \left( {y_{2} P} \right) = A_{3} + B_{3} \rho_{1} + C_{3} T$$

(9)

where A₃ and C₃ are the model parameters.

Bartle et al., model⁴⁸

Sublimation enthalpy of the dissolved solids in SCFs is measured with this model and stated as

$$\ln \left( {\frac{{y_{2} P}}{{P_{ref} }}} \right) = A_{4} + \frac{{B_{4} }}{T} + C_{4} \left( {\rho_{1} - \rho_{ref} } \right)$$

(10)

where A₄, B₄ and C₄ are the model parameters. From parameter B₄, sublimation enthalpy is estimated ($\Delta_{sub} H = - B_{4} R$).

Equation of sate (EoS) modeling

There are several EoS models among them Redlich-Kwong (RK), Soave–Redlich–Kwong (SRK) and Peng-Robinson (PR) EoSs are commonly used in correlating solubility of solid compounds in scCO₂.All these models for correlation requires adjustable interaction parameters and they are found to be temperature dependent^49,50. In the year 1986 Kwak and Mansoori developed a new concept in the spirit of van der Waals mixing rules (VdWmrs), which resulted in temperature independent interaction parameters. They have demonstrated the correlating ability of RK and PR EoSs²⁹. However, SRK EoS has not been explored, therefore in this work, the SRK EoS along with Kwak and Mansoori mixing rules are explored and finally two forms of solubility models for SRK EoS model is proposed. More details about the EoS modeling are presented in the following subsections.

RK EoS with Kwak and Mansoori mixing rules²⁹

RK EoS in terms of compressibility factor (Z) is given by

$$Z = \frac{v}{v - b} - \frac{a}{{RT^{1.5} \left( {v + b} \right)}} \,$$

(11)

VdWmrs for RK EoS are expressed as

$$a = \frac{{\left( {\sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} x_{j} a_{ij}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} b_{ij}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} } } } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}{{\left( {\sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} x_{j} b_{ij}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} } } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}$$

(12)

$$b = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} x_{j} b_{ij} } }$$

(13)

$$a_{ij} = \left( {1 - k_{ij} } \right)\sqrt {a_{ii} a_{jj} }$$

(14)

$$b_{ij} = \left( {1 - l_{ij} } \right)\frac{{\left( {b_{ii}^{{^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }} + b_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} } \right)^{3} }}{8}$$

(15)

Equations (12) to (15) combined with Eq. (11), will constitute the RK EoS for mixtures, consistent with the statistical-mechanical basis of the VdW mixing rules.

PR EoS with Kwak and Mansoori mixing rules^29,49,50

PR EoS in terms of compressibility factor (Z) is given by

$$Z = \frac{v}{v - b} - \frac{{{\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a {RT}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RT}$}} + c - 2\sqrt {\frac{ac}{{RT}}} }}{{\left( {v + b} \right) + \left( {{\raise0.7ex\hbox{$b$} \!\mathord{\left/ {\vphantom {b v}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$v$}}} \right)\left( {v - b} \right)}} \,$$

(16)

where

$$a{\kern 1pt} \left( T \right) = 0.45724\frac{{R^{2} T_{c}^{2} }}{{P_{c} }}\alpha \left( {T_{r} ,\omega } \right) \,$$

$$\alpha \left( {T_{r} ,\omega } \right) = \left[ {1 + \left( {0.37464 + 1.5422\omega - 0.26992\omega^{2} \left( {1 - \sqrt {T_{r} } } \right)} \right)} \right]^{2}$$

$$b = 0.07780\frac{{RT_{c} }}{{P_{c} }}$$

$$a = a \, (T_{c} ) \, \left( {1 + m} \right)^{2} \, and \, c = {\raise0.7ex\hbox{${a \, (T_{c} ) \, m^{2} \, }$} \!\mathord{\left/ {\vphantom {{a \, (T_{c} ) \, m^{2} \, } {RT_{c} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RT_{c} }$}}$$

Equation (16) provides three independent constants in terms of a, b and c. Now following the guidelines given by Kwak and Mansoori mixing rules result in the following expressions for a, b and c

$$a = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} a_{ij}$$

(17)

$$b = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} b_{ij}$$

(18)

$$c = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} c_{ij}$$

(19)

With the following interaction parameters

$${\text{a}}_{{{\text{ij}}}} = \left( {1 - k_{ij} } \right)\sqrt {a_{ii} } a_{jj}$$

(20)

$${\text{b}}_{{{\text{ij}}}} = \left( {{\text{1 - l}}_{{{\text{ij}}}} } \right) \, \left( {\frac{{{\text{b}}_{{{\text{ii}}}}^{{{\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} + b_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}{2}} \right)^{{3}}$$

(21)

$${\text{ c}}_{{{\text{ij}}}} = \left( {{\text{1 - m}}_{{{\text{ij}}}} } \right) \, \left( {\frac{{{\text{c}}_{{{\text{ii}}}}^{{{\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} + c_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}{2}} \right)^{{3}}$$

(22)

Equations (17) to (22) combined with Eq. (16), will constitute the PR EoS for mixtures, consistent with the statistical-mechanical basis of the VdW mixing rules.

SRK EoS with Kwak and Mansoori mixing rules³⁸

In the following, SRK EoS is given by⁵¹

$$P = \frac{RT}{{V - b}} - \frac{a\left( T \right)}{{V\left( {V + b} \right)}} \,$$

(23)

where V is the molar volume and other parameters have usual meanings. The pure component parameter a, which is a function of temperature and b, which is a constant and they are obtained from the following relations.

$$a\left( T \right) = 0.42748\frac{{R^{2} T_{c}^{2} }}{{P_{c} }}\alpha \left( T \right) \,$$

(24)

$$b = 0.08664\frac{{RT_{c} }}{{P_{c} }} \,$$

(25)

$$\alpha \left( T \right) = \left( {1 + m\left( {1 - \sqrt {\frac{T}{{T_{c} }}} } \right)} \right)^{2} \,$$

(26)

where m is a constant given by

$$m = 0.48 + 1.574\omega - 0.176\omega^{2}$$

(27)

where ‘ω’ is the acentric factor. In 1993, Soave proposed a new α(T) function for heavy hydrocarbons to be used with SRK EoS⁵²

$$\alpha \left( T \right) = 1 + m\left( {1 - \frac{T}{{T_{c} }}} \right) + n\left( {1 - \sqrt {\frac{T}{{T_{c} }}} } \right)^{2}$$

(28)

where

$$m = 0.484 + 1.515\omega - 0.044\omega^{2} \quad$$

(29)

$$and\quad n = 2.756m - 0.7 \,$$

(30)

In order to separate thermodynamic variables from constants of the SRK EoS, we have adopted the following two ways.

When Eqs. (26), (27) and (23) are combined to get the following form for SRK EoS in terms of compressibility factor (Z)

$$Z = \frac{v}{v - b} - \frac{{{\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a {RT}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RT}$}} + c - 2\sqrt {\frac{ac}{{RT}}} }}{v + b} \,$$

(31)

where

$$a = a \, (T_{c} ) \, \left( {1 + m} \right)^{2} {\text{ and c}} = {\raise0.7ex\hbox{${{\text{a (T}}_{{\text{c}}} {\text{) m}}^{{2}} \, }$} \!\mathord{\left/ {\vphantom {{{\text{a (T}}_{{\text{c}}} {\text{) m}}^{{2}} \, } {RT_{c} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RT_{c} }$}}$$

This form of the SRK EoS suggests three independent constants namely a, b and c. Now following the guidelines given by Kwak and Mansoori mixing rules result in following expressions for a, b and c

$$a = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} a_{ij}$$

(32)

$$b = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} b_{ij}$$

(33)

$$c = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} c_{ij}$$

(34)

With the following interaction parameters:

$${\text{a}}_{{{\text{ij}}}} = \left( {1 - k_{ij} } \right)\sqrt {a_{ii} } a_{jj}$$

(35)

$${\text{ b}}_{{{\text{ij}}}} = \left( {{\text{1 - l}}_{{{\text{ij}}}} } \right) \, \left( {\frac{{{\text{b}}_{{{\text{ii}}}}^{{{\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} + b_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}{2}} \right)^{{3}} \,$$

(36)

$${\text{ c}}_{{{\text{ij}}}} = \left( {{\text{1 - m}}_{{{\text{ij}}}} } \right) \, \left( {\frac{{{\text{c}}_{{{\text{ii}}}}^{{{\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} + c_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}{2}} \right)^{{3}} \,$$

(37)

Equations (32) to (37) combined with Eq. (31), will constitute the SRK EoS for mixtures, consistent with the statistical-mechanical basis of the VdW mixing rules.

When Eqs. (28), (29), (30) and (23) are combined to get the following form.

$$Z = \frac{v}{v - b} - \frac{{{\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a {RT}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RT}$}} + c - {\raise0.7ex\hbox{$d$} \!\mathord{\left/ {\vphantom {d {\sqrt T }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt T }$}}}}{v + b} \,$$

(38)

where

$$a = a \, (T_{c} ) \, \left( {1 + m + n} \right){\text{ , c}} = \frac{{a \, (T_{c} ) \, \left( {n - m} \right)}}{{RT_{c} }}{\text{ and d}} = {\raise0.7ex\hbox{${{\text{2n a (T}}_{{\text{c}}} )}$} \!\mathord{\left/ {\vphantom {{{\text{2n a (T}}_{{\text{c}}} )} {R\sqrt {T_{c} } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R\sqrt {T_{c} } }$}}$$

This form of the SRK EoS suggests that four independent constants exist in the EoS namely a, b, c and d. Now following the guidelines given by Kwak and Mansoori mixing rules results in following expressions for a, b, c and d

$$a = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} a_{ij}$$

(39)

$$b = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} b_{ij}$$

(40)

$$c = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} c_{ij}$$

(41)

$$d = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} } } x_{j} d_{ij}$$

(42)

With the following interaction parameters:

$${\text{a}}_{{{\text{ij}}}} = \left( {1 - k_{ij} } \right)\sqrt {a_{ii} } a_{jj}$$

(43)

$${\text{ b}}_{{{\text{ij}}}} = \left( {{\text{1 - l}}_{{{\text{ij}}}} } \right) \, \left( {\frac{{{\text{b}}_{{{\text{ii}}}}^{{{\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} + b_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}{2}} \right)^{{3}}$$

(44)

$${\text{ c}}_{{{\text{ij}}}} = \left( {{\text{1 - m}}_{{{\text{ij}}}} } \right) \, \left( {\frac{{{\text{c}}_{{{\text{ii}}}}^{{{\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} + c_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}{2}} \right)^{{3}} \,$$

(45)

$${\text{ d}}_{{{\text{ij}}}} = \left( {{\text{1 - n}}_{{{\text{ij}}}} } \right) \, \left( {\frac{{{\text{d}}_{{{\text{ii}}}}^{{{\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} {3}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3}$}}}} + d_{jj}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}{2}} \right)^{{3}}$$

(46)

Equations (39) to (46) combined with Eq. (38), will constitute the SRK EoS for mixtures, consistent with the statistical-mechanical basis of the VdW mixing rules.

EoS model for the solubility of solids in scCO₂

The mole fraction of dissolved solid drug i (solute) in Solvent scCO₂ is expressed as⁵³

$${\text{y}}_{{\text{i}}} = \frac{{P_{i}^{S} \hat{\phi }_{i}^{S} }}{{P\hat{\phi }_{i}^{{ScCO_{2} }} }}\exp \left[ {\frac{{\left( {P - P_{i}^{S} } \right)v_{S} }}{RT}} \right] \,$$

(47)

where $P_{i}^{s}$ is the sublimation pressure and other parameters have usual meanings. The saturation fugacity coefficient ($\hat{\phi }_{i}^{s}$) is assumed to be unity. The required expression for the solid solute fugacity coefficient in the ScCO₂($\left( {\hat{\phi }_{i}^{{ScCO_{2} }} } \right)$) is calculated using three cubic EoS along with Kwak and Mansoori mixing rules. They are obtained from the following basic thermodynamic relation⁵⁴

$$\ln \left( {\hat{\varphi }_{i}^{{ScCO_{2} }} } \right) = \frac{1}{RT}\int\limits_{v}^{\infty } {\left[ {\left( {\frac{\partial P}{{\partial N_{i} }}} \right)_{{T,V,N_{j} }} - \frac{RT}{v}} \right]} dv - \ln Z$$

(48)

Equations (49) to (52) represent the fugacity coefficients expressions used in this study;

For RK EoS

$$\begin{gathered} \ln \left( {\hat{\varphi }_{i}^{{ScCO_{2} }} } \right) = \ln \left( {\frac{v}{v - b}} \right) + \left( {\frac{{2\sum {x_{j} b_{ij} - b} }}{v - b}} \right) - \ln \left( Z \right) + \hfill \\ \left( {\frac{{a\left( {2\sum {x_{j} b_{ij} - b} } \right)}}{{b^{2} RT^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}} \right)\left[ {\ln \left( {\frac{v + b}{v}} \right) - \frac{b}{v + b}} \right]\left( {3\alpha^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {{\left( {\sum {x_{j} a_{ij}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} b_{ij}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum {x_{j} a_{ij}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} b_{ij}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} } } \right)} {b^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}} \right. \kern-\nulldelimiterspace} {b^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} - \alpha^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \left( {{{\sum {x_{j} b_{ij} } } \mathord{\left/ {\vphantom {{\sum {x_{j} b_{ij} } } {b^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}} \right. \kern-\nulldelimiterspace} {b^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}} \right)} \right)/bRT^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \hfill \\ \end{gathered}$$

(49)

For PR EoS

$${\text{ln}}\left( {\hat{\phi }_{{\text{i}}}^{ScF} } \right) = \left( {\frac{{2\hat{B}}}{b} - 1} \right) \, \left( {\text{Z - 1}} \right){\text{ - ln}}\left[ {{\text{Z}}\left( {{1 - }\frac{b}{v}} \right)} \right] \, + \left[ {\frac{\Delta }{\sqrt 2 RTb}} \right] \, \times {\text{ln}}\left[ {\frac{{{1} + \left( {{1} + \sqrt {2} } \right)\frac{b}{v}}}{{{1} + \left( {{1 - }\sqrt {2} } \right)\frac{b}{v}}}} \right] \,$$

(50)

where

$$\begin{gathered} \Delta = \left[ {\frac{E}{2} - \frac{{E\hat{B}}}{b} + \hat{A}\left( {1 - \sqrt {{\raise0.7ex\hbox{${RTc}$} \!\mathord{\left/ {\vphantom {{RTc} a}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$a$}}} } \right) + \hat{C}\left( {RT - \sqrt {{\raise0.7ex\hbox{${RTa}$} \!\mathord{\left/ {\vphantom {{RTa} c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}} } \right)} \right] \hfill \\ E = a + cRT - 2\sqrt {acRT} ;\hat{A} = \sum {x_{i} } a_{ij} ;\hat{B} = \sum {x_{i} } b_{ij} {\text{and }}\hat{C} = 2\sum {x_{i} } c_{ij} \hfill \\ \end{gathered}$$

For SRK EoS

When three parameters are considered

$$\ln \left( {\hat{\phi }_{i}^{ScF} } \right) = \frac{{\hat{b}}}{b} \, \left( {Z - 1} \right) \, - \ln \left[ {Z\left( {1 - \frac{b}{v}} \right)} \right] \, + \left[ {\frac{{E\hat{b}}}{{b^{2} RT}} - \frac{{\hat{E}}}{bRT}} \right] \, \ln \left( {1 + \frac{b}{v}} \right)$$

(51)

where

$$\begin{gathered} E = a + cRT - 2\sqrt {acRT} \hfill \\ \hat{E} = \frac{1}{N}\frac{{\partial \left( {N^{2} E} \right)}}{{\partial N_{i} }} = \hat{a} \, \left( {1 - \sqrt {{\raise0.7ex\hbox{${RTc}$} \!\mathord{\left/ {\vphantom {{RTc} a}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$a$}}} } \right) + \hat{c}\left( {RT - \sqrt {{\raise0.7ex\hbox{${RTa}$} \!\mathord{\left/ {\vphantom {{RTa} c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}} } \right) \hfill \\ \hat{a} = 2\sum {x_{i} } a_{ij} ,\,\,\hat{b} = 2\sum {x_{i} } b_{ij} - b\;{\text{and}}\,\hat{c} = 2\sum {x_{i} } c_{ij} \hfill \\ \end{gathered}$$

When four parameters are considered

$$\ln \left( {\hat{\phi }_{i}^{ScF} } \right) = \frac{{\hat{b}}}{b} \, \left( {Z - 1} \right) \, - \ln \left[ {Z\left( {1 - \frac{b}{v}} \right)} \right] \, + \left[ {\frac{{E\hat{b}}}{{b^{2} RT}} - \frac{{\hat{E}}}{bRT}} \right] \, \ln \left( {1 + \frac{b}{v}} \right)$$

(52)

where

$$\begin{gathered} E = a + cRT - dR\sqrt T \hfill \\ \hat{E} = \frac{1}{N}\frac{{\partial \left( {N^{2} E} \right)}}{{\partial N_{i} }} = \hat{a} + RT\hat{c} - R\sqrt T \hat{d} \hfill \\ \hat{a} = 2\sum {x_{i} } a_{ij} { , }\quad \hat{b} = {2}\sum {x_{i} } b_{ij} - b{ , }\quad \hat{c} = 2\sum {x_{i} } c_{ij} {\text{ and }}\hat{d} = 2\sum {x_{i} } d_{ij} \hfill \\ \end{gathered}$$

For the data regression, fminsearch (MATLAB 2019) algorithm has been used. Solubility models are regressed with the following objective function⁵⁵

$$OF = \sum\limits_{i = 1}^{N} {\frac{{\left| {y_{2i}^{\exp } - y_{2i}^{calc} } \right|}}{{y_{2i}^{\exp } }}}$$

(53)

Final results are indicated in terms of an average absolute relative deviation percentage (AARD %).

$${\text{AARD}}\left( {\text{\% }} \right) = \left( {{\raise0.7ex\hbox{${100}$} \!\mathord{\left/ {\vphantom {{100} {N_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{i} }$}}} \right)\sum\limits_{i = 1}^{N} {\frac{{\left| {y_{2i}^{\exp } - y_{2i}^{cal} } \right|}}{{y_{2i}^{\exp } }}} .$$

(54)

Results and discussion

The reliability of the experimental setup for the solubility measurement was reported in our previous works with naphthalene and alphatocopherol compounds. Crizotinib’s solubilities in scCO₂ at various conditions are reported in Table 2. Table 2 also indicates scCO₂ density obtained from NIST database⁵⁶. Table 3 indicates solubility range of some of the anticancer drugs reported in the literature. For the Crizotinib the measured solubilities are observed to range from 0.156 × 10⁻⁵ to 1.219 × 10⁻⁵ in mole fraction. Figure 2 indicates solubility isotherms and at 14.5 MPa cross over region is observed. Solubility of pure Crizotinib in scCO₂ the crossover point (14.5 MPa) is rather unique with respect to temperature. Below 14.5 MPa rise in temperature causes drop in solubility in scCO₂ phase, while above this point the opposite effect occurs. The following two ways of thermodynamic explanation may be attributed to this phenomenon as at pressures below the crossover pressure the density of the scCO₂ is more sensitive to temperature changes than at higher pressures. A temperature decrease in this region affects the solubility of the drug in two ways. The vapor pressure of the drug solid decrease while the density of the scCO₂ (proportional to its solvent power) increase thus the density effect predominates and results in the solubility increase. While on the other hand at pressures above the crossover pressure a temperature increase causes an increase the vapor pressure of the drug while the density of the scCO₂ decrease thus the vapor pressure effect predominates and the solubility increases⁵⁷. Another way to explain crossover pressure is that at crossover pressure the partial molar configurational enthalpy equals the negative of the sublimation enthalpy⁵⁸. Table 4 indicates all the standard solubility models utilized in this work. Furthermore, it also indicates all the regressed parameters along with AARD%. The correlating ability of these models are shown in Figs. 3, 4, 5 and 6. The solubility data reported in this study is considered self-consistent since all the data is aligned to a single correlation line (Fig. 5). From literature it is clear that Chrastiland modified Chrastil models are useful in calculating thermodynamic properties like heat of reaction and solvation enthalpy of the dissolution process, therefore these models are considered for the correlating the data^31,33.The total enthalpy of Crizotinib’s dissolution in scCO₂ is calculated from the Chrastil model parameter A₁(i.e., $\Delta H_{total} = - A_{1} R$). The sublimation enthalpy of Crizotinibis calculated from Bartle model parameter (i.e.,$\Delta H_{sub} = - B_{4} R$). Sublimation and solvation are the two major steps in dissolution process and the enthalpy of solvation is calculated from the difference between $\Delta H_{total} - \Delta H_{sub}$. A negative sign is attributed to the solvation process. Similar, this approach is used to calculate all these thermodynamic quantities for modified Chrastil and Bartle models combination, thus estimated values are presented in Table 5.

Table 2 Solubility of crystalline Crizotinib in scCO₂ at various temperatures and pressures.

Table 3 Solubility information of the anticancer drugs.

Figure 2

Solubility isotherms of Crizotinib in scCO₂.

Table 4 Standard solubility models parameters.

Figure 3

Crizotinib solubility in scCO₂ versus ρ₁. Symbols are experimental data points. Solid lines are calculated solubilities with Chrastil model.

Figure 4

Crizotinib solubility in scCO₂ versus ρ₁. Symbols are experimental data points. Solid lines are calculated solubilities with Modified Chrastil model.

Figure 5

Self-consistency plot based on MT model.

Figure 6

ln(y₂ P/P_ref) vs. (ρ₁–ρ_ref). Symbols are experimental data points. Solid lines are calculated solubilities with Bartle et al., model.

Table 5 Calculated thermodynamic properties for Crizotinibin solubility.

The cubic EoS model requires critical properties of Crizotinib and CO₂ and these are estimated with group contribution methods based on the chemical structure^54,59,60,61. Table 6 presents all the estimated critical and physical properties of the drug considered this work. The EoS model regression results are tabulated in Table 7 along with some statistical parameters. From the AARD% it is clear that existing models (RK, SRK EoSs (three parameters) and PR EoS) are poorly correlating the solubility data (Supplementary information Fig. S1, S2, S3). The Crizotinib-scCO₂ system is highly nonlinear system and to correlate such behavior we may need more adjustable parameter, therefore a new form of solubility model based on Kwak and Mansoori guidelines for SRK EoS is proposed. In the new model, one extra parameter is introduced in the term ‘a’ when compared to existing three parameter SRK EoS. Since more parameters are present in the model the regression results will be better in terms of AARD%. Thus, the proposed SRK EoS model is having four parameters. Further the new EoS model is found to correlate the data better than the existing EoS models. From the AARD% it is clear that four parameter SRK EoS correlates the solubility data much better than PR EoS model. Experimental data points and four parameter SRK EoS model predictions are depicted in Fig. 7. Due to poor correlation the RK, PR and three parameter SRK EoSs results are not shown as figures. Overall, four parameter SRK EoS is able to provide satisfactory solubility correlation results. The success of four parameter SRK EoS may be attributed to its number of parameters that constitute the model.

Table 6 Critical and physical properties of Crizotinibinand CO₂^a.

Table 7 Calculated results for the Cubic EoS + Kwak and Mansoori mixing rules.

Figure 7

Crizotinib solubility in scCO₂ vs. P. Symbols are experimental data points. Solid lines are calculated solubilities with SRK EoS + Kwak and Mansoori mixing rules (four parameters model).

Goodness of the models is quantified using an indicator known as Akaike Information Criterion (AIC) and corrected AIC (AIC_c)^62,63,64. As we know, if the experimental data points are less thanforty, the AIC_c is employed. An expression that relates AIC_c with AIC, number of data points (N) and number of parameters in the model ($Q$), is

$$AIC_{c} = AIC + \frac{{2Q\left( {Q + 1} \right)}}{N - Q - 1}$$

(55)

where AIC is $N\;\ln \left( {{{SSE} \mathord{\left/ {\vphantom {{SSE} N}} \right. \kern-\nulldelimiterspace} N}} \right) + 2Q$ and SSE is error sum of squares. According to this indicator, the best model would have least AIC_c value. The summary of AIC, AIC_c, SSE and RMSD values for various models are presented in Table 8. From AIC_c values, it is clear that Chrastil and modified Chrastil models are the better models, whereas four parameter SRK EoS model is the best model among EoS models.

Table 8 Models and their statistical parameters.

Conclusions

Solubilities of Crizotinib in ScCO₂ at various conditions are presented at (T = 308, 318, 328 and 338 K) and (P = 12, 15, 18, 21, 24 and 27 MPa), for the first time. The measured solubilities are in the range from 0.156 × 10⁻⁵ to 1.219 × 10⁻⁵ in terms of mole fraction. The obtained data was modeled with four standard models and three EoS models combining with Kwak and Mansoori mixing rules. Chrastil and Modified Chrastil models are observed to correlate the data with least AARD% and AIC_c values. Among EoS models, four parameter SRK EoS model is able to correlate the data satisfactorily and on par with standard models. Finally, all the standard solubility models considered in this study are able to provide reasonable solubility results.