Abstract
The observation of quantum oscillations in underdoped cuprates has generated intense debate about the nature of the field-induced resistive state and its implications for the ‘normal state’ of high-Tc superconductors. Quantum oscillations suggest an underlying Fermi liquid at high magnetic fields H and low temperatures, in contrast with the pseudogap seen in zero-field, high-temperature spectroscopic experiments. Recent specific heat measurements show quantum oscillations in addition to a large field-dependent suppression of the electronic density of states. Here we present a theoretical analysis that reconciles these seemingly contradictory observations. We model the resistive state as a vortex liquid with short-range d-wave pairing correlations. We show that this state exhibits quantum oscillations, with a period determined by a Fermi surface reconstructed by a competing order parameter, in addition to a large suppression of the density of states that goes like √H at low fields.
Similar content being viewed by others
Introduction
The ‘normal state’ of the high-Tc superconducting cuprates remains an enigma. In the underdoped regime, close to the Mott insulator, a large pseudogap ( meV) is observed in the electronic excitations by a variety of spectroscopic and thermodynamic probes for T>Tc (refs 1,2,34) in the absence of a magnetic field H. It thus came as a great surprise when quantum oscillations were observed5,6 in the low-T regime, once superconductivity is destroyed by H>Hirr, the irreversibility field. Such oscillations, periodic in 1/H, are most easily understood in terms of a Fermi liquid state. This raises the questions: How can one reconcile the high-T, zero-field pseudogap state with the low-T, high-field quantum oscillations? How does a 50-T field have such a dramatic impact on a state with a large 50 meV pseudogap? What is the role of the strong correlation Mott physics in the quantum oscillations?
meV) is observed in the electronic excitations by a variety of spectroscopic and thermodynamic probes for T>Tc (refs 1,2,34) in the absence of a magnetic field H. It thus came as a great surprise when quantum oscillations were observed5,6 in the low-T regime, once superconductivity is destroyed by H>Hirr, the irreversibility field. Such oscillations, periodic in 1/H, are most easily understood in terms of a Fermi liquid state. This raises the questions: How can one reconcile the high-T, zero-field pseudogap state with the low-T, high-field quantum oscillations? How does a 50-T field have such a dramatic impact on a state with a large 50 meV pseudogap? What is the role of the strong correlation Mott physics in the quantum oscillations?
A very important recent development is the electronic specific heat measurements7 in high magnetic fields. These data show quantum oscillations riding on top of a strongly suppressed specific heat with a  singularity at low fields. This unusual H dependence points to the importance of the nodal structure of the d-wave superconducting gap8 even in the resistive state. This raises the further question of reconciling the Fermi surface (FS) probed by quantum oscillations with the nodes of the d-wave gap.
singularity at low fields. This unusual H dependence points to the importance of the nodal structure of the d-wave superconducting gap8 even in the resistive state. This raises the further question of reconciling the Fermi surface (FS) probed by quantum oscillations with the nodes of the d-wave gap.
The specific heat  mJ mol−1 K−2 measured at H=50 T (ref. 7) is greatly suppressed relative to the normal state
mJ mol−1 K−2 measured at H=50 T (ref. 7) is greatly suppressed relative to the normal state  mJ mol−1 K−2 from H=0 experiments9 and band structure estimates γ≃20 mJ mol−1 K−2 (ref. 10). This large suppression suggests that the normal state is not recovered at accessible fields in the quantum oscillation experiments, and one should model the system as a vortex liquid with phase fluctuations arising from mobile vortices. The importance of phase fluctuations has also been emphasized in the analysis of nonlinear diamagnetism11 and Nernst effect12 in the high-temperature normal state, but this interpretation of Nernst data has been recently challenged13. We should note, however, that there is considerable evidence in underdoped cuprates that superconducting order is destroyed by phase-disordering14,15,16,17 rather than a gap collapse, with Tc controlled by the superfluid density. This is exactly what one expects in a lightly doped Mott insulator18.
mJ mol−1 K−2 from H=0 experiments9 and band structure estimates γ≃20 mJ mol−1 K−2 (ref. 10). This large suppression suggests that the normal state is not recovered at accessible fields in the quantum oscillation experiments, and one should model the system as a vortex liquid with phase fluctuations arising from mobile vortices. The importance of phase fluctuations has also been emphasized in the analysis of nonlinear diamagnetism11 and Nernst effect12 in the high-temperature normal state, but this interpretation of Nernst data has been recently challenged13. We should note, however, that there is considerable evidence in underdoped cuprates that superconducting order is destroyed by phase-disordering14,15,16,17 rather than a gap collapse, with Tc controlled by the superfluid density. This is exactly what one expects in a lightly doped Mott insulator18.
In this paper, we address the puzzles described above by investigating the electronic excitations in a vortex liquid. This is a state with a non-zero local d-wave pairing amplitude in which mobile vortices lead to phase fluctuations that make superconducting correlations short ranged in both space and time. Our analysis generalizes earlier studies of the mixed state of s-wave superconductors19,20,21 in two ways—d-wave pairing and dynamical phase fluctuations—both of which are very important for quantum oscillations in cuprates.
We demonstrate that our theoretical approach permits us to reconcile the various seemingly contradictory aspects of the spectroscopy, quantum oscillations and specific heat data. Specifically, we show that the effect of phase fluctuations on the electronic self-energy leads to 1/H periodic quantum oscillations riding on top of a strongly suppressed density of states (DOS) that goes like  at small magnetic fields H. However, we need more than just phase fluctuations to understand the quantum oscillation experiments. Their observed frequency in underdoped cuprates (unlike that in overdoped samples22) is known to be too small to be consistent with a Luttinger FS, and corresponds to an electron-like FS with area of only about 2% of the Brillouin zone (BZ)5,6. It is widely believed10,23,24,25,26 that these observations imply that the FS has been reconstructed by a (possibly field-induced) density-wave order, for which there is now independent experimental evidence27,28,29. Thus, to get a complete description of the underdoped cuprate experiments, we incorporate both phase fluctuations and a competing order parameter in our formalism. This gives rise to an oscillation frequency that agrees with experiment and a singular
at small magnetic fields H. However, we need more than just phase fluctuations to understand the quantum oscillation experiments. Their observed frequency in underdoped cuprates (unlike that in overdoped samples22) is known to be too small to be consistent with a Luttinger FS, and corresponds to an electron-like FS with area of only about 2% of the Brillouin zone (BZ)5,6. It is widely believed10,23,24,25,26 that these observations imply that the FS has been reconstructed by a (possibly field-induced) density-wave order, for which there is now independent experimental evidence27,28,29. Thus, to get a complete description of the underdoped cuprate experiments, we incorporate both phase fluctuations and a competing order parameter in our formalism. This gives rise to an oscillation frequency that agrees with experiment and a singular  suppression of the DOS in the low-field limit, as seen in Riggs7.
suppression of the DOS in the low-field limit, as seen in Riggs7.
Results
Phase fluctuations
We characterize the vortex-liquid state with a simple ansatz for the gauge-invariant correlation function  The complex field Ψμν(r, t) describes singlet pairs on the bond
The complex field Ψμν(r, t) describes singlet pairs on the bond  with a being the Cu–Cu lattice spacing of the CuO2 square lattice with sites r;
with a being the Cu–Cu lattice spacing of the CuO2 square lattice with sites r;  and A is the vector potential for the magnetic field
and A is the vector potential for the magnetic field  The retarded correlation function
The retarded correlation function

is assumed to be short ranged in space and time; Θ(t) is the Heaviside step function. Δ is the local d-wave pairing amplitude that persists above Hirr, as expected for a superconductor where the resistive transition is governed by phase fluctuations. The d-wave nature is described by Sμv=1 for μ=±v and −1 otherwise. The spatial decay in equation (1) is on the magnetic length scale  set by the average inter-vortex separation in the extreme type-II limit. Such a form for the spatial part is natural for a vortex state and can be motivated by considering a disordered vortex assembly or by using Ginzburg–Landau theory, as discussed in Maki19, Stephen20 and Maniv21 for the s-wave case. We work in a regime where the cyclotron radius
set by the average inter-vortex separation in the extreme type-II limit. Such a form for the spatial part is natural for a vortex state and can be motivated by considering a disordered vortex assembly or by using Ginzburg–Landau theory, as discussed in Maki19, Stephen20 and Maniv21 for the s-wave case. We work in a regime where the cyclotron radius  where ξ0 is the vortex core radius and
where ξ0 is the vortex core radius and  is the interparticle spacing.
is the interparticle spacing.
The temporal decay in equation (1) is governed by an energy scale ħΓ that characterizes vortex motion. On general grounds, we expect 0<Γ≤vF/ℓ. The upper limit arises from ballistic motion of vortices with the Fermi velocity vF. For simplicity, we write Γ=αvF/ℓ with 0<α≤1 in the dynamic case where vortices are mobile. The separable form (equation (1)) simplifies the algebra, but a more elaborate non-separable correlator with Γ=Dq2, where D is the vortex diffusion coefficient, is not expected to change our conclusions qualitatively30,31. We will also find it useful to compare our results for dynamic phase fluctuations (Γ≠0) with the static case  with time-independent phase fluctuations19,20,21.
with time-independent phase fluctuations19,20,21.
We use the simplest approximation for self-energy Σ (inset of Fig. 1a) to find the effect of phase fluctuations on electronic excitations in the vortex-liquid state. Our approach generalizes the static, s-wave analysis of Maki19 and Stephen20. A similar self-energy has also been used for the pseudogap phase of cuprates30,31,32, but no calculations have been presented for quantum oscillations.
DOS at the chemical potential NH(0) normalized by the zero-field normal state N0(0). The magnetic field H, measured in units of chemical potential μ, is ħωc /μ with the cyclotron frequency ωc=eH/m*c. We use  (see equation (1)), and an impurity broadening γ0=0.01 in units of μ=1. (a) NH(0) versus 1/H for the static and dynamic cases (Γ≠0) analysed in the LL basis, for the high-field regime nF∼μ/ħωc≲30. The DOS for LLs with Δ=0 is also shown. Note the (1/H) periodicity of the oscillations and the difference in the damping between the static and dynamic cases. The inset shows the self-energy approximation (see text). (b) H-dependent suppression of DOS computed in the LL basis in the low-field regime where nF≲50. We show that
(see equation (1)), and an impurity broadening γ0=0.01 in units of μ=1. (a) NH(0) versus 1/H for the static and dynamic cases (Γ≠0) analysed in the LL basis, for the high-field regime nF∼μ/ħωc≲30. The DOS for LLs with Δ=0 is also shown. Note the (1/H) periodicity of the oscillations and the difference in the damping between the static and dynamic cases. The inset shows the self-energy approximation (see text). (b) H-dependent suppression of DOS computed in the LL basis in the low-field regime where nF≲50. We show that  for small H. (c) DOS obtained from the k-space and semiclassical quantization schemes for
for small H. (c) DOS obtained from the k-space and semiclassical quantization schemes for  ;
;  is the magnetic length.
is the magnetic length.
The central quantity of interest to understand quantum oscillations is the single-particle DOS at the chemical potential N(0) at T=0 as a function of the external field H. We use the self-energy Σ to compute the electronic Green’s function  where G0 is the free Green’s function. The imaginary part of G then gives us the DOS N(ω). We note that there is no anomalous part of the Green’s function, because 〈Ψμ(r, t)〉=0 in the absence of long-range phase coherence. We will focus first on the simple case of parabolic dispersion, where we can do the calculation in two different ways: in Landau level (LL) basis and in momentum (k) space. We then use the k-space approach to shed light on the crucial role of the dynamics of phase fluctuations. Finally, we examine quantum oscillations for arbitrary dispersion using semiclassical quantization of k-space results.
where G0 is the free Green’s function. The imaginary part of G then gives us the DOS N(ω). We note that there is no anomalous part of the Green’s function, because 〈Ψμ(r, t)〉=0 in the absence of long-range phase coherence. We will focus first on the simple case of parabolic dispersion, where we can do the calculation in two different ways: in Landau level (LL) basis and in momentum (k) space. We then use the k-space approach to shed light on the crucial role of the dynamics of phase fluctuations. Finally, we examine quantum oscillations for arbitrary dispersion using semiclassical quantization of k-space results.
LL analysis
Consider electrons with a dispersion ɛk=ħ2k2/2m* and chemical potential μ in a magnetic field H. m* is the effective mass of the electron. In the LL basis, G0(n, iωl)=(iωl−ξn)−1, where ωl=(2l+1)πT is the fermionic Matsubara frequency and the spectrum ξn=(n+1/2)ħ ωc−μ, with cyclotron frequency ωc=(eH/m*c) and LL index n. Using this G0 and the fluctuation propagator Dμν, we obtain the self-energy (see Methods) making the approximation of retaining only diagonal terms in the LL self-energy matrix Σ(n,n′; iωl). We then calculate the DOS  with ω measured from μ. Within the perturbative self-energy approximation (Fig. 1a inset), the LL basis serves as a natural choice because in a magnetic field, electrons form LLs in the absence of pairing (Δ=0), and the bare propagator G0 is diagonal in the LL basis for such a ‘normal’ state. All results shown here are for T=0.
with ω measured from μ. Within the perturbative self-energy approximation (Fig. 1a inset), the LL basis serves as a natural choice because in a magnetic field, electrons form LLs in the absence of pairing (Δ=0), and the bare propagator G0 is diagonal in the LL basis for such a ‘normal’ state. All results shown here are for T=0.
We show in Fig. 1a the DOS NH(0) in a field H, normalized to the H=0 normal state N0(0). Both curves in Fig. 1a exhibit quantum oscillations periodic in (1/H) with the usual Onsager frequency given by the FS area. The index along x axis directly counts the number of filled LL nF∼μ/ħωc. There is, however, a striking difference between the damping of the static (black curve) and dynamic (red curve) results in Fig. 1a. In the static case, the oscillations decay rapidly as exp (−π/τωc) from the large intrinsic damping, 1/τ∼|ImΣ(nF,0)|≠0, arising from scattering of electrons from static-phase fluctuations. (We note that the static d-wave oscillations, though strongly damped, still are much less than the static s-wave results19,20 due to the averaging over the sign changes in the local-order parameter.) In contrast, there is no intrinsic damping in the dynamic case, for which ImΣ(nF,0)=0. The damping in Fig. 1a arises from a small impurity broadening 1/τ0∼γ0 put in by hand in G0, and inevitably present in real materials. Below, we will gain insight into why the intrinsic damping due to dynamic phase fluctuations vanishes. This has direct implication for quantum oscillations in cuprates, where no perceptible damping, in addition to that expected from impurity scattering, has been observed.
In Fig. 1b, we plot NH(0)/N0(0) as a function of H (rather than 1/H) for low fields with nF of order hundred. Quantum oscillations are seen only for Γ≠0 and completely suppressed for the static case. We also see a large, H-dependent DOS suppression relative to the zero-field normal state, with, as we show below, a  singularity at small H. Quantitatively, the suppression depends on Γ, becoming larger with decreasing Γ and most pronounced in the static case. The DOS suppression also depends on the pairing strength Δ, which we take to be H independent, as is reasonable for low fields above Hirr, where the transition to non-superconducting state is due to phase-disordering.
singularity at small H. Quantitatively, the suppression depends on Γ, becoming larger with decreasing Γ and most pronounced in the static case. The DOS suppression also depends on the pairing strength Δ, which we take to be H independent, as is reasonable for low fields above Hirr, where the transition to non-superconducting state is due to phase-disordering.
Momentum space analysis
To gain insight into the LL results, we turn to a k-space analysis. The self-energy Σ(k, iωl) is calculated using the fluctuation propagator equation (1) with G0(k, iωl)=(iωl−ɛk+μ)−1 (see Methods for details). We first look at ɛk=ħ2k2/2m* and then generalize to arbitrary dispersion later.
It is helpful to look at the one-electron spectral function A(k, ω)=−(1/π)ImG(R)(k, ω). We show that dynamical phase fluctuations restore a zero-energy quasiparticle30,31 at the antinodal kF. We may think of this as quantum motional narrowing, with the effect of pairing on the spectral function washed out on the longest time scales, as we now describe in detail.
We plot in Fig. 2a–c the spectral functions for static case with time-independent phase fluctuations, that should be contrasted with the corresponding results in Fig. 2d–f for the dynamic case with Γ≠0. In the static case, we see in Fig. 2a–c that phase fluctuations broaden the nodes of the d-wave superconductor into ‘Fermi arcs’, a region of gapless excitations where the spatial fluctuation-induced line width  overwhelms the gap Δk=Δ[cos (kxa)−cos (kya)]/2. There is a pseudogap in the antinodal region where
overwhelms the gap Δk=Δ[cos (kxa)−cos (kya)]/2. There is a pseudogap in the antinodal region where  as seen in both panels. We note that the static case is not the (highly singular) limit Γ→0 at T=0, but more closely related to the high-temperature regime where T>Γ; see Methods. In the high-T regime, the phase fluctuations are classical32,33 and we can ignore their time dependence. Thus, the physics of the static results is relevant for high-T experiments like angle-resolved photoemission spectroscopy. On the other hand, the quantum oscillation experiments are in the very different low-T limit, where the dynamics of phase fluctuations cannot be ignored.
as seen in both panels. We note that the static case is not the (highly singular) limit Γ→0 at T=0, but more closely related to the high-temperature regime where T>Γ; see Methods. In the high-T regime, the phase fluctuations are classical32,33 and we can ignore their time dependence. Thus, the physics of the static results is relevant for high-T experiments like angle-resolved photoemission spectroscopy. On the other hand, the quantum oscillation experiments are in the very different low-T limit, where the dynamics of phase fluctuations cannot be ignored.
False colour plots of A(k, ω). (a) A(k, ω=0), for static-phase fluctuations contributing to the self-energy Σ(k,0), showing intensity along Fermi arcs near the nodes. We use a parabolic dispersion with H=0.003 (as in Fig. 1, we express H in units of μ=1 and  ). (b) ω versus k dispersion near the AN along a cut perpendicular to the FS, showing a Bogoliubov-like dispersion with a AN pseudogap. (c) Gapless dispersion near the node (NN). We show both the AN and NN momentum cuts in a. (d) A(k, ω=0), for dynamic phase fluctuations (with
). (b) ω versus k dispersion near the AN along a cut perpendicular to the FS, showing a Bogoliubov-like dispersion with a AN pseudogap. (c) Gapless dispersion near the node (NN). We show both the AN and NN momentum cuts in a. (d) A(k, ω=0), for dynamic phase fluctuations (with  ), shows the restoration of the full FS. (e,f) Similar to plots (b,c) for the dynamical case. Note particularly the appearance of a zero-energy quasiparticle inside the pseudogap in the AN cut (e) due to quantum motional narrowing (see text).
), shows the restoration of the full FS. (e,f) Similar to plots (b,c) for the dynamical case. Note particularly the appearance of a zero-energy quasiparticle inside the pseudogap in the AN cut (e) due to quantum motional narrowing (see text).
The results with Γ≠0 dynamics are qualitatively different from the static case. We see from Fig. 2d that one recovers the full FS, albeit with a highly anisotropic self-energy, as illustrated by the A(k, ω) dispersion plots in Fig. 2e, along two representative momentum cuts perpendicular to the FS, one near the antinode (AN) in the superconducting state and the other near the node (NN). We can understand the appearance of the zero-energy quasiparticle at the AN by looking at the self-energy. In contrast to the static case, which has a large antinodal |ImΣ(kF, ω)| at low energies, dynamical phase fluctuations lead to |ImΣ(kF, ω)|∼ω2 for |ω|<<Γ, the quantum motional narrowing mentioned above. The corresponding ImΣ(kF, ω) then leads to a quasiparticle pole at the chemical potential, even though the self-energy effects are strongly k dependent as seen from Fig. 2e.
The existence of sharp quasiparticles all around the full FS immediately leads to the quantum oscillations with the Onsager frequency. We define a renormalized dispersion  for low-energy quasiparticles, which has a non-trivial H dependence from the self-energy. We then use a semiclassical prescription34 to quantize the orbits (see Methods). The resulting DOS from this k-space analysis is shown in Fig. 1c, with a small impurity scattering γ0 that damps the quantum oscillations.
for low-energy quasiparticles, which has a non-trivial H dependence from the self-energy. We then use a semiclassical prescription34 to quantize the orbits (see Methods). The resulting DOS from this k-space analysis is shown in Fig. 1c, with a small impurity scattering γ0 that damps the quantum oscillations.
The most non-trivial aspect of this result is that the quantum oscillations ride on top of a large, field-dependent suppression of the DOS NH(0), just as we saw in the LL analysis (Fig. 1b). We can analyse this suppression by looking at the ‘average’ DOS (without any semiclassical quantization), shown as the dashed curve in Fig. 1c. We can show analytically in the static case that the H-dependent self-energy Σ(k, 0) leads to  as H→0 (see Methods), where the residual value arises from impurity scattering γ0. This reproduces the celebrated Volovik result8 from quite a different route, and generalizes it to include impurities. Even though the same value of γ0 is used in the LL calculation of Fig. 1b, the residual value is not recovered in this calculation, presumably due to the additional ‘diagonal approximation’ (see Methods), which neglects the off-diagonal elements of Σ that become larger with decreasing field.
as H→0 (see Methods), where the residual value arises from impurity scattering γ0. This reproduces the celebrated Volovik result8 from quite a different route, and generalizes it to include impurities. Even though the same value of γ0 is used in the LL calculation of Fig. 1b, the residual value is not recovered in this calculation, presumably due to the additional ‘diagonal approximation’ (see Methods), which neglects the off-diagonal elements of Σ that become larger with decreasing field.
FS reconstruction by a competing order
The analysis presented above shows that although phase fluctuations are able to reconcile quantum oscillations with a large suppression of the DOS that goes like  , they do not affect the oscillation frequency. Thus, to get a complete description of the underdoped cuprate experiments, we need to incorporate both phase fluctuations and a competing order. We can incorporate any one of the proposed broken symmetries10,23,24,25,26 within our k-space formulation. Only experiments will decide which competing order is most relevant for a particular material. Once superconducting long-range order is destroyed by the field, it is natural that the ground state of a lightly doped Mott insulator exhibits a new density-wave instability that reconstructs the FS. However, we are firmly of the opinion that the large (
, they do not affect the oscillation frequency. Thus, to get a complete description of the underdoped cuprate experiments, we need to incorporate both phase fluctuations and a competing order. We can incorporate any one of the proposed broken symmetries10,23,24,25,26 within our k-space formulation. Only experiments will decide which competing order is most relevant for a particular material. Once superconducting long-range order is destroyed by the field, it is natural that the ground state of a lightly doped Mott insulator exhibits a new density-wave instability that reconstructs the FS. However, we are firmly of the opinion that the large ( meV) AN pseudogap cannot arise from a small (or subtle) symmetry breaking, and it is not reasonable to use a large symmetry breaking potential to reconstruct the FS.
meV) AN pseudogap cannot arise from a small (or subtle) symmetry breaking, and it is not reasonable to use a large symmetry breaking potential to reconstruct the FS.
To understand the interplay of FS reconstruction and phase fluctuations, we analyse, as an illustrative example, the density-wave order proposed in Yao et al.10 with  consistent with recent high-field nuclear magnetic resonance data27 Following Yao et al.10, we start with ɛk=−2t[(1+φN) cos kxa+(1−φN) cos kya]−4t′ cos kxa cos kya, where t (t′) is the nearest (next-nearest) neighbour hopping and φN the nematicity. Phase fluctuations renormalize this dispersion to
consistent with recent high-field nuclear magnetic resonance data27 Following Yao et al.10, we start with ɛk=−2t[(1+φN) cos kxa+(1−φN) cos kya]−4t′ cos kxa cos kya, where t (t′) is the nearest (next-nearest) neighbour hopping and φN the nematicity. Phase fluctuations renormalize this dispersion to  with the self-energy discussed above. To find the FS reconstruction, we diagonalize the Hamiltonian
with the self-energy discussed above. To find the FS reconstruction, we diagonalize the Hamiltonian

where V and V′ are the density-wave potentials.
We semiclassically quantize the resulting energy dispersion. The results are shown in Fig. 3. The chemical potential is fixed for x≈0.12. As shown in Fig. 3a, there are small electron-like FS pockets and open FS sheets. The pockets have an area around 2% of the original BZ and there is only one pocket in the new BZ. Although the open FS sheets do not contribute to oscillations of DOS, they give rise to large contribution to DOS in the absence of pairing. In a vortex liquid, these DOS from the open orbits are largely suppressed as shown in Fig. 3b. Hence, in this case the frequency as well as the suppression of DOS are both in good agreement with experiments5,6,7.
(a) Open and closed FS segments shown in the original BZ (BZ) for density-wave order scenario of Yao et al.10 We choose parameters t′/t=−0.4, φN=0.143, V=0.11t and V′=0.09t (enhanced Vs to make the reconstruction visible) with μ=−1.05t. (b) DOS quantum oscillations obtained from semiclassical quantization of the reconstructed FS in a vortex-liquid state. Here t′/t=−0.4, φN=0.143, V=0.02t, V′=0.01t with μ=−1.05t, so that the hole doping x≈0.12 and the closed orbit area  2% of the BZ. The DOS also includes the contributions of open orbits. The H-dependent suppression of the DOS arises from phase fluctuations with
2% of the BZ. The DOS also includes the contributions of open orbits. The H-dependent suppression of the DOS arises from phase fluctuations with  and
and  . Here γ0=0.01t.
. Here γ0=0.01t.
Discussion
In conclusion, we emphasize aspects of our results that point to interesting new research directions. We pointed out the dichotomy between classical thermal fluctuations, leading to a pseudogap and the dynamics of phase fluctuations restoring the zero-energy quasiparticles via quantum motional narrowing at low temperatures. This is difficult to probe using current experimental tools because angle-resolved photoemission spectroscopy cannot be done in an external magnetic field. However, as other spectroscopic tools, such as c-axis optical conductivity and scanning tunnelling microscopy become possible in large H fields, one should be able to directly probe the near-antinodal DOS. We hope that, in the future, high-field scanning tunnelling microscopy studies will be directly able to probe both the field-induced competing order and its impact on the low-energy quasiparticle excitations that give rise to quantum oscillations.
Methods
Electronic Green’s function in a d-wave vortex liquid
The d-wave pairing field  is defined on the link
is defined on the link  at imaginary time τ with 0≤τ≤β≡1/T. We set ħ=1 here. The diagonal and off-diagonal Green’s functions G and F satisfy the Gor'kov equations:
at imaginary time τ with 0≤τ≤β≡1/T. We set ħ=1 here. The diagonal and off-diagonal Green’s functions G and F satisfy the Gor'kov equations:


where we use the short-hand notation G(1;1′)≡G(r1,τ1;r1′,τ1′),  ,
,  and ∫2,2′≡ ∫dr2dr2′∫0βdτ2dτ2′. The indices μ and ν run over bond directions
and ∫2,2′≡ ∫dr2dr2′∫0βdτ2dτ2′. The indices μ and ν run over bond directions  . The factors 1/16 and 1/4 are related to the normalization of Ψ.
. The factors 1/16 and 1/4 are related to the normalization of Ψ.
Generalizing the s-wave approach of Stephen20, we first average equation (2a) and (2b) over the configurations {Ψμ(r, τ)} and then make the decoupling approximation


By definition 〈Ψμ(r2,τ2)〉=0 in a vortex liquid, which implies that 〈F(r1,τ1;r′1,τ′1)〉=0.
For notational simplicity, we omit 〈…〉 from now on. We can write the averaged equation (2a) as

Here G(1,1′;l)≡G(r1,r1′; iωl),  ,
,  and (−l+m) ≡− iωl+iΩm where ωl=(2l+1)πT and Ωm=2mπT are Fermi and Bose Matsubara frequencies, ∫2,2′≡∫dr2dr2′ and
and (−l+m) ≡− iωl+iΩm where ωl=(2l+1)πT and Ωm=2mπT are Fermi and Bose Matsubara frequencies, ∫2,2′≡∫dr2dr2′ and  . The separable form of equation (1) leads to
. The separable form of equation (1) leads to

where  and
and  is the Matsubara representation of the dissipative form
is the Matsubara representation of the dissipative form 
The integral ∫0rA·dl in  is taken along the straight line from 0 to r, as explained in Stephen20 for the s-wave case. The d-wave case also has the phase factor
is taken along the straight line from 0 to r, as explained in Stephen20 for the s-wave case. The d-wave case also has the phase factor  arising from the pair field on the bonds of the lattice.
arising from the pair field on the bonds of the lattice.
LL analysis
We choose the Landau gauge  . For a parabolic dispersion the Green’s functions in the LL basis is
. For a parabolic dispersion the Green’s functions in the LL basis is  . Here φnq(r) is the LL wave function with n the LL index and q goes over the degenerate states in each LL. We rewrite equation (3) in the LL basis in the form G=G0+G0ΣG. The bare G0(nq,n′q′;iωl)≡(iωl−ξn)−1δnn′δqq′ The self-energy
. Here φnq(r) is the LL wave function with n the LL index and q goes over the degenerate states in each LL. We rewrite equation (3) in the LL basis in the form G=G0+G0ΣG. The bare G0(nq,n′q′;iωl)≡(iωl−ξn)−1δnn′δqq′ The self-energy

In the dynamic case, the Matsubara sum can be done using  given below equation (4). For the static case, Dμν(r,τ) is independent of τ, so that
given below equation (4). For the static case, Dμν(r,τ) is independent of τ, so that  and the Matsubara sum is trivial. We discuss below how the static case is recovered in the high-temperature, classical limit of the dynamic case.
and the Matsubara sum is trivial. We discuss below how the static case is recovered in the high-temperature, classical limit of the dynamic case.
We can express Iμν in terms of special functions. (We omit the details of this lengthy algebra here.) The self-energy Σ then turns out to be diagonal in q-space and also independent of q in the translationally invariant vortex liquid. Unlike the s-wave case20, Σ is a matrix in the LL index due to the d-wave symmetry. It can be shown that the matrix elements Σ(n,n′;iωl) decay rapidly away from the diagonal n=n′ like  . In the spirit of our non-self-consistent calculation (Fig. 1a (inset)), given that G0 is diagonal in the LL index, we only retain the dominant diagonal terms in Σ(n,n; iωl)≡Σ(n, iωl). The k-space analysis described below serves to validate this approximation.
. In the spirit of our non-self-consistent calculation (Fig. 1a (inset)), given that G0 is diagonal in the LL index, we only retain the dominant diagonal terms in Σ(n,n; iωl)≡Σ(n, iωl). The k-space analysis described below serves to validate this approximation.
ImΣ with iωl→ω+i0+ is given by

Here 
 , Ln(x) is a Laguerre polynomial and
, Ln(x) is a Laguerre polynomial and  . ReΣ can be obtained using the Kramers–Kronig relation. For large values of the LL index n, we derive a useful approximation
. ReΣ can be obtained using the Kramers–Kronig relation. For large values of the LL index n, we derive a useful approximation

where J0(x) denotes a Bessel function. We have benchmarked this form by comparing it with results obtained directly from equation (6) and found that the approximation is accurate for nF=(μ/ωc) 10. We have used equation (7) for computing the results reported in the paper. We have also found expressions analogous to equations (6) and (7) for the static case, for example, at large n.
10. We have used equation (7) for computing the results reported in the paper. We have also found expressions analogous to equations (6) and (7) for the static case, for example, at large n.

k-space analysis
The k-space calculation of self-energy is used together with a semiclassical approach to quantum oscillations for μ>Δ>>ωc. One can make a gauge transformation and represent G(r,r′;iωl) as

where  depends only on the separation r'−r. We rewrite equation (3) in terms of
depends only on the separation r'−r. We rewrite equation (3) in terms of  or its Fourier transform G(k,iωl) (we omit the tilde to simplify notation) and obtain the corresponding self-energy
or its Fourier transform G(k,iωl) (we omit the tilde to simplify notation) and obtain the corresponding self-energy

Here Δk=(Δ/2)( cos kxa −cos kya) and  .
.
In the semiclassical regime where μ>>ωc or the cyclotron radius Rc>> , we neglect the effects of quantization of electronic orbits while evaluating Σ(k, iωl) and approximate G0(k, iωl) by (iωl−ξk)−1. Further, in the field regime of interest,
, we neglect the effects of quantization of electronic orbits while evaluating Σ(k, iωl) and approximate G0(k, iωl) by (iωl−ξk)−1. Further, in the field regime of interest,  >>ξ0 and
>>ξ0 and  are sharply peaked around q=0 with a width
are sharply peaked around q=0 with a width  . We thus expand
. We thus expand  and
and  , where vk=(∂ξk/∂k). Proceeding in a manner similar to the LL discussion above
, where vk=(∂ξk/∂k). Proceeding in a manner similar to the LL discussion above

Here vk=|vk| and we take the T=0 limit at the end. The corresponding Σ(k,ω) in the static case is

where  and
and  is the Dawson function.
is the Dawson function.
Semiclassical quantization
We use the semiclassical prescription for quantizing electron orbits with the renormalized dispersion  . For a given field H, we generate a set of energy levels
. For a given field H, we generate a set of energy levels  as the solutions of
as the solutions of  , where
, where  is the k-space area enclosed by a closed orbit at energy
is the k-space area enclosed by a closed orbit at energy  and n is a positive integer. We then use
and n is a positive integer. We then use  s to compute the DOS.
s to compute the DOS.
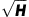 behaviour
behaviour
At asymptotically low fields, we use the static self-energy (equation 12) that reduces to the standard d-wave form  as
as  . For small H, we expand Σ(k, ω=0) in p=k−kN around one of the four nodes at kN, with
. For small H, we expand Σ(k, ω=0) in p=k−kN around one of the four nodes at kN, with  and
and  . We get
. We get  and
and  , where vΔ=|∂Δk/∂k| and vF are evaluated at kN. Using this field dependence of Σ(k,0) in the spectral function leads to
, where vΔ=|∂Δk/∂k| and vF are evaluated at kN. Using this field dependence of Σ(k,0) in the spectral function leads to  as H→0, thus recovering Volovik’s result8.
as H→0, thus recovering Volovik’s result8.
We can further generalize the above analysis to include impurity scattering γ0. To make the algebra tractable, we approximate the Gaussian in equation (12) by a Lorentzian, so that  , where γ0<<Δ≤μ comes from weak impurity scattering. The Lorentzian form results from static pair correlator
, where γ0<<Δ≤μ comes from weak impurity scattering. The Lorentzian form results from static pair correlator  and gives rise to qualitatively similar low-energy electronic spectra as the Gaussian. Expanding near the nodes we obtain
and gives rise to qualitatively similar low-energy electronic spectra as the Gaussian. Expanding near the nodes we obtain

to leading order in  . Here the momentum cut-off
. Here the momentum cut-off  . This implies that
. This implies that  as H→0 in excellent agreement with the numerical results shown in the text. (A and B are appropriate constants that depend logarithmically on γ0.)
as H→0 in excellent agreement with the numerical results shown in the text. (A and B are appropriate constants that depend logarithmically on γ0.)
The high-temperature limit and the static case
The static case is related to the high-temperature regime T>>Γ, and not the (highly singular) Γ→0 limit of the dynamic case. In the high T limit, the classical, thermal fluctuations that dominate are time independent. For T>>Γ, we see that Ω<<T in the integral in equation (11), and we can set  ,
,  . To make analytical progress, we approximate 1/(Ω2+Γ2) by
. To make analytical progress, we approximate 1/(Ω2+Γ2) by  to obtain
to obtain

This has exactly the same form as the static case equation (12) with the redefinitions (TΔ2/Γ)→Δ2 and  . For a closely related discussion, see Micklitz and Norman31.
. For a closely related discussion, see Micklitz and Norman31.
Additional information
How to cite this article: Banerjee, S. et al. Theory of quantum oscillations in the vortex-liquid state of high-Tc superconductors. Nat. Commun. 4:1700 doi: 10.1038/ncomms2667 (2013).
References
Timusk, T. & Statt, B. The pseudogap in high-temperature superconductors: an experimental survey. Rep. Prog. Phys. 62, 61–122 (1999).
Damascelli, A., Hussain, Z. & Shen, Z. X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Campuzano, J. C., Norman, M. R. & Randeria, M. Photoemission in the high-Tc superconductors. in Superconductivity eds Bennemann K. H., Ketterson J. B.) Vol 2, (Springer Verlag: Berlin, (2008).
Kanigel, A. et al. Evolution of the pseudogap from Fermi arcs to the nodal liquid. Nat. Phys. 2, 447–451 (2006).
Doiron-Leyraud, N. et al. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature 447, 565–568 (2007).
Sebastian, S. E. et al. A multi-component Fermi surface in the vortex state of an underdoped high-Tc superconductor. Nature 454, 200–203 (2008).
Riggs, S. C. et al. Heat capacity through the magnetic-field-induced resistive transition in an underdoped high-temperature superconductor. Nat. Phys. 7, 332–335 (2011).
Volovik, G. E. Superconductivity with lines of gap nodes: density of states in the vortex. JETP Lett. 58, 469–473 (1993).
Loram, J. W., Mirza, K. A., Cooper, J. R. & Liang, W. Y. Electronic specific heat of YBa2Cu3O6+x from 1.8 to 300 K. Phys. Rev. Lett. 71, 1740–1743 (1993).
Yao, H., Lee, D.-H. & Kivelson, S. Fermi-surface reconstruction in a smectic phase of a high-temperature superconductor. Phys. Rev. B 84, 012507- (2011).
Li, L. et al. Diamagnetism and Cooper pairing above Tc in cuprates. Phys. Rev. B 81, 054510- (2010).
Wang, Y., Li, L. & Ong, N. P. Nernst effect in high-Tc superconductors. Phys. Rev. B 73, 024510- (2006).
Chang, J. et al. Decrease of upper critical field with underdoping in cuprate superconductors. Nat. Phys. 8, 751–756 (2012).
Uemura, Y. J. et al. Universal correlations between Tc and ns/m* (carrier density over effective mass) in high-Tc cuprate cuperconductors. Phys. Rev. Lett. 62, 2317–2320 (1989).
Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1994).
Broun, D. M. et al. Superfluid density in a highly underdoped YBa2Cu3O6+y superconductor. Phys. Rev. Lett. 99, 237003- (2007).
Hetel, I., Lemberger, T. R. & Randeria, M. Quantum critical behaviour in the superfluid density of strongly underdoped ultrathin copper oxide films. Nat. Phys. 3, 700–702 (2007).
Paramekanti, A., Randeria, M. & Trivedi, N. Projected wave functions and high temperature superconductivity. Phys. Rev. Lett. 87, 217002 (2001).
Maki, K. Quantum oscillation in vortex states of type-II superconductors. Phys. Rev. B 44, 2861–2862 (1991).
Stephen, M. J. Superconductors in strong magnetic fields: de Haas van Alphen effect. Phys. Rev. B 45, 5481–5485 (1992).
Maniv, T., Zhuravlev, V., Vagner, I. & Wyder, P. Vortex states and quantum magnetic oscillations in conventional type-II superconductors. Rev. Mod. Phys. 73, 867–911 (2001).
Vignolle, B. et al. Quantum oscillations in an overdoped high-Tc superconductor. Nature 455, 952–955 (2008).
Millis, A. J. & Norman, M. R. Antiphase stripe order as the origin of electron pockets observed in 1/8-hole-doped cuprates. Phys. Rev. B 76, 220503(R) (2007).
Chakravarty, S. & Kee, H.-Y. Fermi pockets and quantum oscillations of the Hall coefficient in high-temperature superconductors. Proc. Natl Acad. Sci. USA 105, 8835–8839 (2008).
Harrison, N. & Sebastian, S. E. Protected nodal electron pocket from multiple-Q ordering in underdoped high temperature superconductors. Phys. Rev. Lett. 106, 226402- (2011).
Sebastian, S. E., Harrison, N. & Lonzarich, G. G. Quantum oscillations in the high-Tc cuprates. Phil. Trans. R. Soc. A 369, 1687–1711 (2011).
Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy . Nature 477, 191–194 (2011).
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y,Nd)YBa2Cu3O6+x . Science 337, 821–825 (2012).
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67 . Nat. Phys. 8, 871–876 (2012).
Senthil, T. & Lee, P. A. Synthesis of the phenomenology of the underdoped cuprates. Phys. Rev. B 79, 245116- (2009).
Micklitz, T. & Norman, M. R. Nature of spectral gaps due to pair formation in superconductors. Phys. Rev. B 80, 220513(R) (2009).
Banerjee, S., Ramakrishnan, T. V. & Dasgupta, C. Effect of pairing fluctuations on low-energy electronic spectra in cuprate superconductors. Phys. Rev. B 84, 144525 (2011).
Berg, E. & Altman, E. Evolution of the Fermi surface of d-wave superconductors in the presence of thermal phase fluctuations. Phys. Rev. Lett. 99, 247001- (2007).
Luttinger, J. M. Theory of the de Haas-van Alphen effect for a system of interacting fermions. Phys. Rev. 121, 1251–1258 (1961).
Acknowledgements
We gratefully acknowledge stimulating conversations with Steve Kivelson, Mike Norman and Suchitra Sebastian, and the support of DOE-BES DE-SC0005035.
Author information
Authors and Affiliations
Contributions
S.B., S.Z. and M.R. contributed to the theoretical research described in this paper and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Banerjee, S., Zhang, S. & Randeria, M. Theory of quantum oscillations in the vortex-liquid state of high-Tc superconductors. Nat Commun 4, 1700 (2013). https://doi.org/10.1038/ncomms2667
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2667
This article is cited by
-
Connecting high-field quantum oscillations to zero-field electron spectral functions in the underdoped cuprates
Nature Communications (2014)
-
Plane speaking
Nature Physics (2013)
-
Universal quantum oscillations in the underdoped cuprate superconductors
Nature Physics (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






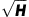 behaviour
behaviour