Fractional magnetoresistance oscillations in spin-triplet superconducting rings

Abstract

Half-quantum vortices in spin-triplet superconductors are predicted to host Majorana zero modes and may provide a viable platform for topological quantum computation. Recent works also suggested that, in thin mesoscopic rings, the superconducting pairing symmetry can be probed via Little-Parks-like magnetoresistance oscillations of periodicity Φ₀ = h/2e that persist below the critical temperature. Here we use the London limit of Ginzburg-Landau theory to study these magnetoresistance oscillations resulting from thermal vortex tunneling in spin-triplet superconducting rings. For a range of temperatures in the presence of disorder, we find magnetoresistance oscillations with an emergent fractional periodicity Φ₀/n, where the integer n ≥ 3 is entirely determined by the ratio of the spin and charge superfluid densities. These fractional oscillations can unambiguously confirm the spin-triplet nature of superconductivity and directly reveal the tunneling of half-quantum vortices in real-world candidate materials.

Introduction

Flux quantization is a defining feature of superconductivity that directly originates from the macroscopic quantum coherence of electron pairs. A salient manifestation of flux quantization (or more precisely, fluxoid quantization) is the Little-Parks effect¹ wherein the resistance of a hollow superconducting cylinder close to its critical temperature oscillates as a function of the magnetic flux inside with a periodicity given by the flux quantum Φ₀ = h/2e. In thin mesoscopic rings where vortex-crossing processes lead to a finite resistance even in the superconducting state, analogous magnetoresistance oscillations with the same periodicity are also observable much below the critical temperature due to a periodic modulation of the vortex-crossing rate^2,3,4,5.

Recently, such magnetoresistance oscillations arising from both the conventional Little-Parks effect^6,7,8,9 and the rate of vortex crossings^10,11 have been identified as a useful tool in the ongoing search for exotic spin-triplet superconductors^{12,13,14,15,16,17,18,19}. In addition to the standard quantum vortices corresponding to fluxoid quantization, these unconventional superconductors may also host half-quantum vortices around which the fluxoid is quantized to a half-integer multiple of Φ₀. With such half-quantum vortices present, the magnetoresistance oscillations are then expected to develop a characteristic two-peak structure^6,11,20. Importantly, half-quantum vortices are also predicted to harbor Majorana zero modes^21,22 whose non-Abelian statistics may enable intrinsically fault-tolerant quantum computation^23,24.

In this work, we theoretically study the magnetoresistance oscillations in thin mesoscopic rings of spin-triplet superconductors below the critical temperature. Focusing on the London limit of Ginzburg-Landau theory, we adopt the formalism in ref. ²⁵ to describe the available fluxoid states and thermal vortex-crossing processes by accounting for both the usual charge supercurrent and the spin supercurrent unique to spin-triplet superconductors. At the lowest temperatures, we verify that the magnetoresistance oscillates with periodicity Φ₀ and has a distinctive two-peak structure^6,11,20. More interestingly, there is an intermediate temperature range in which disorder leads to magnetoresistance oscillations with a fractional periodicity Φ₀/n, where the integer n≥3 is determined by the ratio of the spin and charge superfluid densities²⁶. Since these fractional oscillations directly reflect the enlarged number of available fluxoid states, we argue that they are defining hallmarks of spin-triplet superconductors supporting half-quantum vortices, much like the integer oscillations are for conventional spin-singlet superconductors.

Results and discussion

General formalism

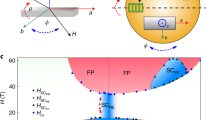
We consider a circular superconducting ring of inner radius R₀ and outer radius ηR₀ in a perpendicular magnetic field $\overrightarrow{H}=H{\overrightarrow{e}}_{\!\!z}$ [see Fig. 1a]. We assume that the ring is made from a superconducting film of thickness t ≪ R₀ and that the superconductor has spin-triplet p_x + ip_y pairing with orbital angular momentum m_l = + 1 with respect to the ${\overrightarrow{e}}_{\!\!z}$ direction. To allow for stable half-quantum vortices in the simplest possible setting, we also assume that spin-orbit coupling forces the spin pairing vector $\overrightarrow{d}$ into the plane perpendicular to ${\overrightarrow{e}}_{\!\!z}$ such that the spin angular momentum is restricted to m_s = ± 1. The spin-triplet superconducting order parameter is then given by²⁶

$$\hat{{{\Delta }}}=\left[\begin{array}{ll}{{{\Delta }}}_{\uparrow \uparrow }&{{{\Delta }}}_{\uparrow \downarrow }\\ {{{\Delta }}}_{\downarrow \uparrow }&{{{\Delta }}}_{\downarrow \downarrow }\end{array}\right]={{{\Delta }}}_{0}{e}^{i\chi }\left[\begin{array}{ll}{e}^{i\alpha }&0\\ 0&-{e}^{-i\alpha }\end{array}\right],$$

(1)

where χ is the usual superconducting phase corresponding to the overall charge supercurrent, while α corresponds to the difference between the spin-up (↑↑) and spin-down (↓↓) supercurrents, i.e., a pure spin supercurrent. In general, the central hole of the ring has a finite vorticity (fluxoid number) for each supercurrent such that χ (α) winds by 2πN_c (2πN_s) along the inner circumference of the ring. To understand how a vortex may travel across the ring, we further consider a vortex at position ${\overrightarrow{r}}_{0}=({r}_{0},0)$ inside the ring [see Fig. 1a] around which χ (α) winds by 2πn_c (2πn_s). Importantly, the order parameter is only single valued if the two numbers within each pair (N_c, N_s) and (n_c, n_s) are either both integer, corresponding to a standard quantum vortex, or both half integer, corresponding to a half-quantum vortex.

Fig. 1: General setup and definitions.

a Thin-film superconducting ring with inner radius R₀ and outer radius ηR₀ in a perpendicular magnetic field $\overrightarrow{H}=H{\overrightarrow{e}}_{z}$. During a snapshot of a vortex-crossing process, the central hole of the ring has charge and spin vorticities (fluxoid numbers) N_c,s, while the vortex at radius r₀ inside the ring has charge and spin vorticities n_c,s. Experimentally, the resistance due to such vortex-crossing processes is found by applying a bias current I to a short section of the ring and measuring the voltage V between the two leads. b Vortex self energy f_nn(ϱ) against the vortex position ϱ = r₀/R₀ for η = 1.2 without disorder (solid line) and with a single pinning site inside the ring (dashed line).

Assuming R₀ ≪ Λ with the Pearl length Λ = 2λ²/t and the penetration depth λ, the magnetic screening inside the superconductor is negligible, and the magnetic field $\overrightarrow{B}$ is identical to the external field $\overrightarrow{H}$²⁵. In the London limit, corresponding to a small coherence length ξ, the magnitude Δ₀ of the order parameter at any position $\overrightarrow{r}$ further than ξ from ${\overrightarrow{r}}_{0}$ is constant, and the Ginzburg-Landau free energy is then²⁶

$$F=\frac{t{{{\Phi }}}_{0}^{2}}{8{\pi }^{2}{\mu }_{0}{\lambda }^{2}}\int{d}^{2}\overrightarrow{r}\left[\left\vert \right.{\overrightarrow{J}}_{\!\!\!c}{\left\vert \right.}^{2}+\gamma \left\vert \right.{\overrightarrow{J}}_{\!\!s}{\left\vert \right.}^{2}\right]$$

(2)

in terms of the effective charge and spin supercurrents

$${\overrightarrow{J}}_{\!\!\!c}=\overrightarrow{\nabla }\chi -\frac{2\pi }{{{{\Phi }}}_{0}}\overrightarrow{A},\,\,{\overrightarrow{J}}_{\!\!s}=\overrightarrow{\nabla }\alpha ,$$

(3)

where the vector potential $\overrightarrow{A}$ satisfies $\overrightarrow{\nabla }\times \overrightarrow{A}=\overrightarrow{B}=\overrightarrow{H}$, while the ratio γ of the spin and charge superfluid densities²⁶ is expected to be smaller than 1 for interacting superconductors^27,28. In the absence of a bias current I [see Fig. 1a], the charge supercurrent must satisfy the differential equations

$$\overrightarrow{\nabla }\cdot {\overrightarrow{J}}_{\!\!\!c}=0,\,\overrightarrow{\nabla }\times {\overrightarrow{J}}_{\!\!\!c}=\left[2\pi {n}_{c}\delta (\overrightarrow{r}-{\overrightarrow{r}}_{0})-\frac{2h}{{R}_{0}^{2}}\right]{\overrightarrow{e}}_{\!\!z}$$

(4)

inside the superconductor, along with the boundary conditions

$${\overrightarrow{e}}_{\!\!\!n}\cdot {\overrightarrow{J}}_{\!\!\!c}=0,\,\,{\oint }_{| \overrightarrow{r}| = {R}_{0}}d\overrightarrow{r}\cdot {\overrightarrow{J}}_{\!\!\!c}=2\pi \left({N}_{c}-h\right)$$

(5)

at any interface with normal unit vector ${\overrightarrow{e}}_{\!\!\!n}$, and along the inner circumference of the ring, respectively, where $h=H{R}_{0}^{2}\pi /{{{\Phi }}}_{0}$ is a dimensionless external field. Importantly, the spin supercurrent ${\overrightarrow{J}}_{\!\!s}$ also satisfies Eqs. (4) and (5) with the substitutions n_c → n_s, N_c → N_s, and h → 0. We further note that Eqs. (4) and (5) are equivalent to those studied in ref. ²⁵.

Due to the linearity of Eqs. (4) and (5), the general solutions for the charge and spin supercurrents can be written as

$${\overrightarrow{J}}_{\!\!\!c}={n}_{c}{\overrightarrow{J}}_{\!\!\!n}+{N}_{c}{\overrightarrow{J}}_{\!\!\!N}-h{\overrightarrow{J}}_{\!\!\!h},\,{\overrightarrow{J}}_{\!\!s}={n}_{s}{\overrightarrow{J}}_{\!\!\!n}+{N}_{s}{\overrightarrow{J}}_{\!\!\!N},$$

(6)

where ${\overrightarrow{J}}_{\!\!\!n}$, ${\overrightarrow{J}}_{\!\!\!N}$, and ${\overrightarrow{J}}_{\!\!\!h}$ are the particular solutions of Eqs. (4) and (5) with (n_c, N_c, h) being equal to (1, 0, 0), (0, 1, 0), and (0, 0, − 1), respectively. Using polar coordinates, $\overrightarrow{r}=(r,\vartheta )$, one readily obtains ${\overrightarrow{J}}_{\!\!\!N}=(1/r){\overrightarrow{e}}_{\!\!\vartheta }$ and ${\overrightarrow{J}}_{\!\!\!h}=(r/{R}_{0}^{2}){\overrightarrow{e}}_{\!\!\vartheta }$, while ${\overrightarrow{J}}_{\!\!\!n}$ for a given vortex position r₀ = ϱR₀ was calculated in ref. ²⁵. Substituting Eq. (6) into Eq. (2), the free energy of the system in the pure (vortex-free) case with n_c,s = 0 is then

$${F}_{{N}_{c},{N}_{s},h}^{{{{{{{{\rm{pure}}}}}}}}}={F}_{0}\left[{f}_{NN}\left({N}_{c}^{2}+\gamma {N}_{s}^{2}\right)-2{f}_{Nh}{N}_{c}h+{f}_{hh}{h}^{2}\right],$$

(7)

while in the presence of a vortex at radius r₀ = ϱR₀ it reads

$${F}_{{N}_{c},{N}_{s},{n}_{c},{n}_{s},h}^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho ) = \, {F}_{{N}_{c},{N}_{s},h}^{{{{{{{{\rm{pure}}}}}}}}}+{F}_{0}\left[{f}_{nn}(\varrho )\left({n}_{c}^{2}+\gamma {n}_{s}^{2}\right)\right.\\ + \,\left.2{f}_{nN}(\varrho )\left({n}_{c}{N}_{c}+\gamma {n}_{s}{N}_{s}\right)-2{f}_{nh}(\varrho )\,{n}_{c}h\right],$$

(8)

where ${F}_{0}=t{{{\Phi }}}_{0}^{2}\ln \eta /(4\pi {\mu }_{0}{\lambda }^{2})$ is an overall energy scale, and ${f}_{XY}={(2\pi \ln \eta )}^{-1}\int{d}^{2}\overrightarrow{r}\,{\overrightarrow{J}}_{X}\cdot {\overrightarrow{J}}_{Y}$ (X, Y = n, N, h) are dimensionless free energies²⁵:

$${f}_{NN}= \, 1,\,\,\,{f}_{Nh}=\frac{{\eta }^{2}-1}{2\ln \eta },\,\,\,{f}_{hh}=\frac{{\eta }^{4}-1}{4\ln \eta },\\ {f}_{nN}(\varrho )= \, 1-\frac{\ln \varrho }{\ln \eta },\,\,\,{f}_{nh}(\varrho )=\frac{{\eta }^{2}-{\varrho }^{2}}{2\ln \eta },$$

(9)

while f_nn(ϱ) has the form plotted in Fig. 1b. We remark that f_nn(ϱ), corresponding to the self energy of the vortex, nominally diverges in the London limit and must be regularized with a small but finite coherence length ξ. We use ξ/R₀ ≈ 0.02 but emphasize that its precise value is not important as f_nn(ϱ) is only logarithmically divergent.

Theory of magnetoresistance

We first assume that the superconducting ring in Fig. 1a is in thermal equilibrium without any bias current I. Because of the large vortex self energy in the London limit, there are no stable vortices inside the superconductor at sufficiently low temperatures. Nonetheless, at any finite temperature T = 1/β, the fluxoid numbers N_c,s of the central hole can thermally fluctuate, and the probability of the system to be in the fluxoid state (N_c, N_s) is given by

$${P}_{({N}_{c},{N}_{s})}=\frac{1}{Z}\exp \left[-\beta {F}_{{N}_{c},{N}_{s},h}^{{{{{{{{\rm{pure}}}}}}}}}\right],$$

(10)

where $Z={\sum }_{{N}_{c},{N}_{s}}\exp [-\beta {F}_{{N}_{c},{N}_{s},h}^{{{{{{{{\rm{pure}}}}}}}}}]$. The thermal fluctuations themselves happen by vortices traveling across the ring; the fluxoid state of the system transitions from (N_c, N_s) to $({N}_{c}^{{\prime} },{N}_{s}^{{\prime} })$ if a vortex with $({n}_{c},{n}_{s})=\kappa ({N}_{c}^{{\prime} }-{N}_{c},{N}_{s}^{{\prime} }-{N}_{s})$ and κ = + 1 (κ = − 1) crosses the ring in the inward (outward) direction. If these two processes are thermally activated, their respective free-energy barriers are²⁵

$${F}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h}^{{{{{{{{\rm{barrier}}}}}}}},+}= \, \mathop{\max }\limits_{\varrho }{F}_{{N}_{c},{N}_{s},{N}_{c}^{{\prime} }-{N}_{c},{N}_{s}^{{\prime} }-{N}_{s},h}^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho ) -{F}_{{N}_{c},{N}_{s},h}^{{{{{{{{\rm{pure}}}}}}}}},\\ {F}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h}^{{{{{{{{\rm{barrier}}}}}}}},-}= \mathop{\max }\limits_{\varrho }{F}_{{N}_{c}^{{\prime} },{N}_{s}^{{\prime} },{N}_{c}-{N}_{c}^{{\prime} },{N}_{s}-{N}_{s}^{{\prime} },h}^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho ) -{F}_{{N}_{c},{N}_{s},h}^{{{{{{{{\rm{pure}}}}}}}}},$$

(11)

and the total transition rate from (N_c, N_s) to $({N}_{c}^{{\prime} },{N}_{s}^{{\prime} })$ is then

$${{{\Gamma }}}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h} = \, {P}_{({N}_{c},{N}_{s})}\,{A}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h},\\ {A}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h} \propto \, \mathop{\sum}\limits_{\pm }\exp \left[-\beta {F}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h}^{{{{{{{{\rm{barrier}}}}}}}},\pm }\right].$$

(12)

We note that, in thermal equilibrium, detailed balance is satisfied: ${{{\Gamma }}}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h}={{{\Gamma }}}_{({N}_{c}^{{\prime} },{N}_{s}^{{\prime} })\to ({N}_{c},{N}_{s}),h}$.

Next, we assume that a bias current I is applied by attaching two leads to the superconducting ring (see Fig. 1a). For each vortex with a given sign of the charge vorticity n_c, the bias current exerts a force in the inward or outward direction, thus leading to a net flow of such vortices in one of these directions by decreasing the free-energy barrier in one direction and increasing it in the other one. The resulting rate of phase slips then gives rise to a finite voltage between the two leads and translates into a finite resistance for the superconducting ring²⁹. Without affecting our main results, we make a simplifying assumption that the two leads are close to each other along the ring (see Fig. 1a). In this case, the entire bias current goes through the short section of the ring between the two leads, and the probabilities ${P}_{({N}_{c},{N}_{s})}$ of the fluxoid states are still given by Eq. (10). However, from the perspective of the transition rates ${A}_{({N}_{c},{N}_{s})\to ({N}_{c}^{{\prime} },{N}_{s}^{{\prime} }),h}$ within the short section, the charge fluxoid number is effectively reduced by ε = I/I₀, where ${I}_{0}=t{{{\Phi }}}_{0}\ln \eta /(2\pi {\mu }_{0}{\lambda }^{2})$. Hence, for a small bias current I ≪ I₀, the resistance between the two leads becomes

$$R\propto \mathop{\sum}\limits_{{N}_{c},{N}_{s}}{P}_{({N}_{c},{N}_{s})}\mathop{\sum}\limits_{{n}_{c},{n}_{s}}{n}_{c}\,\frac{\partial {A}_{({N}_{c}-\varepsilon ,{N}_{s})\to ({\tilde{N}}_{c}-\varepsilon ,{\tilde{N}}_{s}),h}}{\partial \varepsilon }{\Big | }_{\varepsilon = 0},$$

(13)

where ${\tilde{N}}_{c,s}\equiv {N}_{c,s}+{n}_{c,s}$, while ${A}_{({N}_{c}-\varepsilon ,{N}_{s})\to ({\tilde{N}}_{c}-\varepsilon ,{\tilde{N}}_{s}),h}$ for ε ≠ 0 is computed through Eqs. (11) and (12) by formally evaluating Eqs. (7) and (8) at a fractional value of N_c. Finally, to obtain our full set of main results, we assume that the short section of the ring between the two leads contains some form of disorder. For concreteness, we first consider a single localized “pinning site” (e.g., defect or impurity) that renormalizes the vortex self energy from f_nn(ϱ) to ${f}_{nn}^{{\prime} }(\varrho )$ [see Fig. 1b], but later we also demonstrate that our main results are not sensitive to the precise form of disorder.

Fractional oscillations

The resistance R of the superconducting ring is plotted in Fig. 2 against the external field H for different values of the temperature T and the superfluid-density ratio γ. We parameterize the external field in terms of the dimensionless flux ϕ = Φ/Φ₀, where ${{\Phi }}=H{R}_{{{{{{{{\rm{eff}}}}}}}}}^{2}\pi$ is the flux inside the effective mean radius²⁵

$${R}_{{{{{{{{\rm{eff}}}}}}}}}={R}_{0}\sqrt{\frac{{f}_{Nh}}{{f}_{NN}}}={R}_{0}\sqrt{\frac{{\eta }^{2}-1}{2\ln \eta }}.$$

(14)

In this parameterization, conventional magnetoresistance oscillations in spin-singlet superconductors^2,3,4,5 have unit periodicity Δϕ = 1 with a peak at each external field ϕ = N + 1/2 ($N\in {\mathbb{Z}}$) as explicitly confirmed in Supplementary Note 1. In contrast, Fig. 2 shows that spin-triplet superconductors with γ < 1 possess nontrivial additional structure in their magnetoresistance oscillations. For the lowest temperatures (T ≪ F₀), the periodicity is still Δϕ = 1, but each peak at ϕ = N + 1/2 splits into two peaks that move further apart as γ is decreased^6,11,20. For high temperatures (T ≫ F₀), the oscillations are significantly more complex with an overall periodicity Δϕ = 1 or Δϕ = 1/2. Most interestingly, for intermediate temperatures (T ~ F₀), the magnetoresistance oscillations have an emergent fractional periodicity Δϕ = 1/n, where the integer n is determined by the superfluid-density ratio γ. While Fig. 2 suggests that the different integers n≥3 correspond to specific rational values of γ, it is demonstrated in Figs. 3 and 4 that the fractional periodicities Δϕ = 1/n persist in finite ranges of both γ and T. In particular, the Fourier analysis of the oscillation components in Fig. 4 reveals that the fractional periodicities Δϕ = 1/3, Δϕ = 1/4, and Δϕ = 1/5 are observable for 0.25 ≲ γ ≲ 0.45, 0.45 ≲ γ ≲ 0.55, and 0.55 ≲ γ ≲ 0.65, respectively.

Fig. 2: Magnetoresistance oscillations at different temperatures.

Resistance R of the superconducting ring in Fig. 1a, as calculated from Eq. (13), against the dimensionless flux ϕ = Φ/Φ₀ at low temperatures T = F₀/10 (a–c), intermediate temperatures T = F₀ (d–f), and high temperatures T = 5F₀ (g–i) [in terms of ${F}_{0}=t{{{\Phi }}}_{0}^{2}\ln \eta /(4\pi {\mu }_{0}{\lambda }^{2})$] for a radius ratio η = 1.2 and superfluid-density ratios γ = 1/3 (a, d, g), γ = 1/2 (b, e, h), and γ = 3/5 (c, f, i) in the presence of a single pinning site inside the ring [see Fig. 1b].

Fig. 3: Robustness of fractional oscillations.

Magnetoresistance oscillations with fractional periodicities Δϕ = 1/3 (a–c) and Δϕ = 1/4 (d–f) in the intermediate temperature ranges 0.3 ≤ T/F₀≤ 1.5 and 0.6 ≤ T/F₀≤ 1.2 for superfluid-density ratios 0.3 ≤ γ ≤ 0.36 and 0.48 ≤ γ ≤ 0.52, respectively. In each case, the resistance R of the superconducting ring in Fig. 1a is calculated from Eq. (13) against the dimensionless flux ϕ = Φ/Φ₀ for a radius ratio η = 1.2 in the presence of a single pinning site inside the ring [see Fig. 1b]. The different curves are labeled by γ and are vertically shifted with respect to each other for better visibility.

Fig. 4: Robustness of fractional periodicities.

Fourier amplitudes ${\tilde{R}}_{n}\propto | \int\nolimits_{0}^{1}d\phi \,R(\phi )\,{e}^{2\pi in\phi }|$ of the magnetoresistance components corresponding to the fractional periodicities Δϕ = 1/n with n = 3 (dots), n = 4 (crosses), and n = 5 (circles) against the superfluid-density ratio γ at the intermediate temperature T = F₀. For each γ, the magnetoresistance R(ϕ) of the superconducting ring in Fig. 1a is calculated from Eq. (13) for a radius ratio η = 1.2 in the presence of a single pinning site inside the ring [see Fig. 1b].

To understand these fractional oscillations, we first notice that the free energy of a pure (vortex-free) system in Eq. (7) can be written in the new parameterization as

$${F}_{{N}_{c},{N}_{s},\phi }^{{{{{{{{\rm{pure}}}}}}}}}={F}_{0}\left[{\left({N}_{c}-\phi \right)}^{2}+\gamma {N}_{s}^{2}+g(\phi )\right].$$

(15)

For external field ϕ, the free-energy difference between two fluxoid states (N_c, N_s) and $({\tilde{N}}_{c},{\tilde{N}}_{s})=({N}_{c}+{n}_{c},{N}_{s}+{n}_{s})$, connected by vortices ± (n_c, n_s) crossing the ring, is then

$${F}_{{\tilde{N}}_{c},{\tilde{N}}_{s},\phi }^{{{{{{{{\rm{pure}}}}}}}}}-{F}_{{N}_{c},{N}_{s},\phi }^{{{{{{{{\rm{pure}}}}}}}}} = \, 2{F}_{0}\left[{n}_{c}\left({N}_{c}-\phi \right)+\gamma {n}_{s}{N}_{s}\right]\\ + {F}_{0}\left({n}_{c}^{2}+\gamma {n}_{s}^{2}\right).$$

(16)

Moreover, if the radius ratio η of the superconducting ring is not too large, f_nN(ϱ) and f_nh(ϱ) in Eq. (9) are close to linear for 1 ≤ ϱ ≤ η. Hence, taking a linear interpolation between their values at ϱ = 1 and ϱ = η, the free energy of the system with a single vortex (see Eq. (8)) can be approximated by

$${F}_{{N}_{c},{N}_{s},{n}_{c},{n}_{s},\phi }^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho )= \, {F}_{{N}_{c},{N}_{s},\phi }^{{{{{{{{\rm{pure}}}}}}}}}+{F}_{0}{f}_{nn}^{{\prime} }(\varrho )\left({n}_{c}^{2}+\gamma {n}_{s}^{2}\right)\\ \, + 2{F}_{0}\left[{n}_{c}\left({N}_{c}-\phi \right)+\gamma {n}_{s}{N}_{s}\right]\frac{\eta -\varrho }{\eta -1}.$$

(17)

Importantly, if we use this approximation, the transition rates ${A}_{({N}_{c},{N}_{s})\to ({N}_{c}+{n}_{c},{N}_{s}+{n}_{s}),\phi }$ in Eq. (12) only depend on either ϕ or N_c,s via the combination n_c(N_c − ϕ) + γn_sN_s, and the resistance in Eq. (13) thus takes the general form

$$R\propto \mathop{\sum}\limits_{{N}_{c},{N}_{s}}{P}_{({N}_{c},{N}_{s})}\mathop{\sum}\limits_{{n}_{c},{n}_{s}}{G}_{{n}_{c},{n}_{s}}\left[{n}_{c}\left({N}_{c}-\phi \right)+\gamma {n}_{s}{N}_{s}\right].$$

(18)

Due to the many identical contributions ${G}_{{n}_{c},{n}_{s}}$ corresponding to different N_c,s, each shifted by N_c + γN_sn_s/n_c in the field ϕ, this form naturally leads to periodic oscillations.

Next, we recall from Eq. (17) that the vortex self energy is proportional to ${n}_{c}^{2}+\gamma {n}_{s}^{2}$. For any γ < 1, the dominant vortices contributing to the resistance at sufficiently low temperatures [$T\ll {F}_{0}\mathop{\max }\limits_{\varrho }{f}_{nn}^{{\prime} }(\varrho )$] are then the half-quantum vortices with n_c,s = ± 1/2. In the intermediate temperature range (T ~ F₀), there are also many fluxoid states (N_c, N_s) with sizeable probabilities ${P}_{({N}_{c},{N}_{s})} \sim 1$. If we then sum over the identical contributions G_±1/2,±1/2 in Eq. (18) for all possible N_c,s, each shifted by N_c ± γN_s in the field ϕ, these identical contributions conspire to produce fractional oscillations with periodicity Δϕ = 1/n. For a rational value of the superfluid-density ratio, γ = p/q, with the integers p and q being relative primes, it is shown in Supplementary Note 2 that n = q if p and q are both odd and n = 2q otherwise. Therefore, in accordance with Fig. 2, the fractional periodicities are Δϕ = 1/3, Δϕ = 1/4, and Δϕ = 1/5 for γ = 1/3, γ = 1/2, and γ = 3/5, respectively. In practice, since the summation over N_c,s is cut off at any finite temperature T ~ F₀, only the fractional periodicities with small p and q are observable, but each of them remains observable in a finite range around γ = p/q (see Figs. 3 and 4). As an interesting aside, we point out that the emergence of fractional oscillations and the intimate connection between Δϕ and γ can also be understood from the simple geometric picture presented in Fig. 5.

Fig. 5: Geometric interpretation of fractional oscillations.

Emergence of the fractional periodicities Δϕ = 1/3 (a), Δϕ = 1/4 (b), and Δϕ = 1/5 (c) from the superfluid-density ratios γ = 1/3, γ = 1/2, and γ = 3/5, respectively. Within a two-dimensional plane, the black dots depict the possible fluxoid states (N_c, N_s), while the red dot at position (ϕ, 0) represents the external field. Due to the scaling factor $\sqrt{\gamma }$ between the vertical (N_s) and horizontal (N_c) dimensions, the energy of a given fluxoid state is proportional to the distance squared between the corresponding black dot and the red dot [see Eq. (15)]. Focusing on the half-quantum transitions n_c,s = ΔN_c,s = 1/2 (dotted lines), the argument (N_c + γN_s − ϕ)/2 of G_1/2,1/2 in Eq. (18) corresponds to the perpendicular projection of the red dot onto the dotted line connecting (N_c, N_s) and (N_c + 1/2, N_s + 1/2). Therefore, as the external field ϕ is increased, the same feature in the magnetoresistance is periodically replicated every time the red dot at position (ϕ, 0) crosses a perpendicular bisector (dashed line). Relevant transitions connecting fluxoid states with sizeable probabilities are within the red circle whose radius scales with the square root of the temperature.

We finally remark that, as the temperature T approaches the critical temperature of the superconductor, the effective temperature T/F₀ with ${F}_{0}=t{{{\Phi }}}_{0}^{2}\ln \eta /(4\pi {\mu }_{0}{\lambda }^{2})$ diverges as a result of λ → ∞. Therefore, in principle, the intermediate temperatures T ~ F₀ that give rise to the fractional magnetoresistance oscillations are attainable for any ring dimensions. In practice, however, we expect the fractional oscillations to be more observable further away from the critical temperature, which is achieved by keeping both the film thickness t and the radius ratio η as small as possible.

Effect of disorder

Remarkably, the fractional magnetoresistance oscillations only emerge if disorder is present in the superconductor. This property is demonstrated in Fig. 6 where the magnetoresistance is plotted without any disorder and with different kinds of disorder: a single pinning site [see Fig. 1b] of two different depths, a collection of three pinning sites, and a random potential landscape (i.e., extended disorder). While the magnetoresistance is completely featureless in the absence of disorder, it exhibits fractional oscillations with the same periodicity if any kind of disorder is included.

Fig. 6: Relation between disorder and fractional oscillations.

Vortex self energy f_nn(ϱ) against the dimensionless vortex position ϱ (a–e) and the corresponding resistance R of the superconducting ring in Fig. 1a against the external field (i.e., dimensionless flux) ϕ = Φ/Φ₀ at the intermediate temperature T = F₀/2 (f–j) for a radius ratio η = 1.2 and a superfluid-density ratio γ = 1/3 without any disorder (a, f), with a single pinning site of a larger depth (b, g) and a smaller depth (c, h), with a collection of three pinning sites (d, i), and with a random potential landscape (e, j).

Indeed, even though the fractional periodicity Δϕ = 1/n is a robust emergent feature connected to the superfluid-density ratio γ, the corresponding oscillations are not observable if the functions G_±1/2,±1/2 are completely smooth. The crucial role of disorder is to produce nonanalytic features in G_±1/2,±1/2 that can be replicated with periodicity Δϕ as a function of the field ϕ. In the following, we restrict our attention to a single pinning site (see Fig. 1b) and describe how it gives nonanalytic features (cusps) in the transition rate A_{(0, 0)→(1/2, 1/2),ϕ} (see Eq. (12)) and hence the function G_1/2,1/2 that manifest as sharp peaks in the magnetoresistance.

From Eq. (12), the transition rate A_{(0, 0)→(1/2, 1/2),ϕ} at any given temperature only depends on the two vortex-crossing barriers ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},\pm }$. The inward vortex-crossing barrier ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},+}$ is plotted in Fig. 7a against the field ϕ and shows a clear cusp at a critical field ${\phi }_{0}^{+}$. Noting that the vortex-crossing barrier ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},+}$ is determined by the maximum of the vortex energy function ${F}_{0,0,1/2,1/2,\phi }^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho )$ in the vortex position ϱ (see Eq. (11)), it is then illustrated in Fig. 7b-d that the critical field ${\phi }_{0}^{+}$ corresponds to a discontinuity in the vortex position ${\varrho }_{0}^{+}$ that maximizes the vortex energy function ${F}_{0,0,1/2,1/2,\phi }^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho )$. Analogously, the outward vortex-crossing barrier ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},-}$ has a cusp at another critical field ${\phi }_{0}^{-}$ corresponding to a discontinuity in the vortex position ${\varrho }_{0}^{-}$ that maximizes the vortex energy function ${F}_{1/2,1/2,-1/2,-1/2,\phi }^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho )$ (see Eq. (11)).

Fig. 7: Connection between disorder and vortex-crossing barriers.

a Vortex-crossing barrier ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},+}$ against the external field ϕ = Φ/Φ₀ for a radius ratio η = 1.2 and a superfluid-density ratio γ = 1/3 with a single pinning site inside the ring [see Fig. 1b]. The dashed line indicates the critical field ${\phi }_{0}^{+}\approx 1/3$ at which the first derivative has a discontinuity. b–d Vortex energy function ${F}_{0,0,1/2,1/2,\phi }^{{{{{{{{\rm{vortex}}}}}}}}}(\varrho )$ against the dimensionless vortex position ϱ for three different external fields: ϕ = 0 (b), ϕ = 1/3 (c), and ϕ = 2/3 (d). In each case, the dashed line marks the maximum of the vortex energy function, i.e., the vortex-crossing barrier in subfigure a. The critical field ${\phi }_{0}^{+}\approx 1/3$ corresponds to a discontinuity in the vortex position ${\varrho }_{0}^{+}$ that maximizes the vortex energy function.

For the particular location of the pinning site in Fig. 1b, the two vortex-crossing barriers have identical critical fields: ${\phi }_{0}^{+}={\phi }_{0}^{-}$ (see Fig. 8a). If the pinning site is moved inward or outward, the two critical fields ${\phi }_{0}^{\pm }$ then shift in opposite directions and are generically different (see Fig. 8b, c). Consequently, the fractional magnetoresistance oscillations may develop a two-peak structure while retaining the same fractional periodicity (see Fig. 8d–f). For more general disorder, we expect multiple features (not necessarily peaks) in the magnetoresistance that are all replicated with the given periodicity Δϕ. While the precise shape and amplitude of the fractional oscillations thus depends on the specific form of disorder, the fractional periodicity Δϕ is universal and only depends on the superfluid-density ratio γ (see Fig. 6).

Fig. 8: Connection between vortex-crossing barriers and magnetoresistance peaks.

Vortex-crossing barriers ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},\pm }$ (a–c) and the corresponding resistance R of the superconducting ring at the intermediate temperature T = F₀/2 (d–f) against the external field ϕ = Φ/Φ₀ for a radius ratio η = 1.2 and a superfluid-density ratio γ = 1/3 with a single pinning site at (a, d) the same location as in Fig. 1b and (b, c, e, f) moved in the inward direction by a smaller amount (b, e) and a larger amount (c, f). The two vortex-crossing barriers ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},+}$ (solid line) and ${F}_{(0,0)\to (1/2,1/2),\phi }^{{{{{{{{\rm{barrier}}}}}}}},-}$ (dash-dotted line) are vertically shifted with respect to each other for better visibility. In each case, the dashed lines indicate the two critical fields ${\phi }_{0}^{\pm }$ that correspond to cusps in the vortex-crossing barriers and peaks replicated with periodicity Δϕ = 1/3 in the magnetoresistance.