Abstract
In multiple quantitative trait locus (QTL) mapping, a high-dimensional sparse regression model is usually employed to account for possible multiple linked QTLs. The QTL model may include closely linked and thus highly correlated genetic markers, especially when high-density marker maps are used in QTL mapping because of the advancement in sequencing technology. Although existing algorithms, such as Lasso, empirical Bayesian Lasso (EBlasso) and elastic net (EN) are available to infer such QTL models, more powerful methods are highly desirable to detect more QTLs in the presence of correlated QTLs. We developed a novel empirical Bayesian EN (EBEN) algorithm for multiple QTL mapping that inherits the efficiency of our previously developed EBlasso algorithm. Simulation results demonstrated that EBEN provided higher power of detection and almost the same false discovery rate compared with EN and EBlasso. Particularly, EBEN can identify correlated QTLs that the other two algorithms may fail to identify. When analyzing a real dataset, EBEN detected more effects than EN and EBlasso. EBEN provides a useful tool for inferring high-dimensional sparse model in multiple QTL mapping and other applications. An R software package ‘EBEN’ implementing the EBEN algorithm is available on the Comprehensive R Archive Network (CRAN).
Similar content being viewed by others
Introduction
Quantitative traits are usually controlled by multiple quantitative trait loci (QTLs) and environmental factors. Because of the physical linkage of multiple QTLs, gene–gene interactions (epistasis) and gene–environment interactions, it is highly desirable to analyze a large number of loci and environmental factors simultaneously in a single QTL model. As technology advancement in molecular genotyping has made high-density genomic markers available, including all markers in a single QTL model leads to a large number of model variables, typically much larger than the sample size. Two techniques often used in the inference of such high dimensional QTL models are variable selection and shrinkage operator.
Variable selection typically employs a stepwise search method in conjunction with a selection criterion such as the Bayesian information criterion (Schwarz, 1978) to identify a subset of all possible genetic effects that best explain the phenotypic variation (Bogdan et al., 2008; Li et al., 2009; Yu et al., 2009). On the other hand, shrinkage methods such as Lasso (Tibshirani, 1996) and Bayesian Lasso (Park and Casella, 2008; Yi and Xu, 2008) include all variables in the model but use a penalty function of the variables or appropriate prior distributions for the variables to shrink most variables toward zero. Especially, the Bayesian shrinkage approach (O'Hara and Sillanpaa, 2009) has received considerable attention recently and been applied to multiple QTL mapping (Xu, 2003; Wang et al., 2005; Hoti and Sillanpää, 2006; Huang et al., 2007; Yi and Xu, 2008). All these Bayesian methods rely on the Markov Chain Monte Carlo (MCMC) simulation to fit the Bayesian model, which is computationally intensive and time consuming when a large number of effects are considered in the model.
Recently, we developed two efficient empirical Bayesian Lasso (EBlasso) algorithms using a two-level hierarchical model with normal and exponential priors (EBlasso-NE) or a three-level hierarchical model with normal, exponential and Gamma priors (EBlasso-NEG) for multiple QTL mapping (Cai et al., 2011; Huang et al., 2013), which was shown to outperform other shrinkage methods including Lasso and MCMC-based Bayesian shrinkage methods in terms of power of detection and false discovery rate (FDR). Similar to Lasso, our EBlasso and other Bayesian shrinkage methods typically selects one variable out of a group of highly correlated variables. When QTLs are located closely, these shrinkage methods may not select all QTLs. Recently, the elastic net (EN) (Zou and Hastie, 2005) was developed to handle the issue of correlated variables in high-dimensional sparse models where only a relatively small number of variables are nonzero. An MCMC-based Bayesian EN method was also proposed (Li and Lin, 2010).
In this paper, capitalizing on the idea of EN, we propose a Bayesian EN (BEN) model for multiple QTL mapping, and then develop a novel empirical Bayesian EN (EBEN) algorithm to infer the BEN model. The EBEN algorithm is very efficient because of a coordinate ascent strategy and other algorithmic techniques used. Simulation studies demonstrate that our EBEN algorithm outperforms EN and EBlasso. Real data analysis demonstrates the utility of our EBEN algorithm.
Materials and methods
Linear model of multiple QTLs
Let yi be the value of a quantitative trait of the ith individual in a mapping population. Suppose we observe yi, i=1, ···, n, of n individuals and collect them into a vector y=[y1, y2, ···, yn]T. In these n individuals, suppose there are p environmental covariates observed and m genetic markers genotyped. Let covariate l and genotype of marker j of individual i be xEil and xGij, respectively. Let us define xEi=[xEi1, xEi2,···, xEip]T and xGi=[xGi1, xGi2,···, xGim]T. Then we have the following linear regression model for y:

where μ is the population mean, vectors βE and βG represent the environmental effects and the genetic effects of all markers, respectively; matrices XE=[xE1, xE2,···, xEn]T and XG=[xG1, xG2,···, xGn]T are the corresponding design matrices of different effects; and ɛ is the residual error that follows a normal distribution with zero-mean and covariance  .
.
The design matrix XG depends on a specific genetic model. We adopt the widely used Cockerham genetic model (Cockerham, 1954), which defines the values of a marker effect as −0.5 and 0.5 for two genotypes in a back cross design, and −1, 0 and 1 for three genotypes having additive effect, and −0.5 and 0.5 for homozygotes and heterozygotes having dominance effect in an intercross (F2) design. For simplicity, we only consider additive effects in (1), although the method developed in this paper is also applicable to the model with dominance effects. Epistatic effects can also be incorporated into (1) as carried out in (Xu, 2007; Cai et al., 2011), and the EBEN algorithm developed in this paper is applicable to the model with epistatic effects. However, for the ease of presentation, we will use model (1) throughout the paper.
Defining  , and X=[XE, XG], we can write (1) in a more compact form:
, and X=[XE, XG], we can write (1) in a more compact form:

Given p environmental covariates and m markers with additive effects, the size of matrix X is n × k where k=p+m. Our goal is to identify all possible environmental effects on and QTLs for y manifested as the nonzero elements of the regression coefficients β. When the number of environmental factors and number of markers are large, β contains a large number of unknowns, which makes model inference a challenging problem. However, we would expect that a small portion of markers are QTLs and a small portion of environmental factors influence the trait, which implies that β is a sparse vector meaning that most elements of β are zero.
We have developed an efficient EBlasso algorithm to infer sparse β from (2). However, we observed that similar to Lasso (Tibshirani, 1996), EBlasso typically outputs at most one nonzero regression coefficient for a group of several highly correlated variables. If several QTLs are relatively close, their correlation is high. For example, if two QTLs have a distance d=5 centi-Morgan (cM), their correlation R=e−2d=0.9 assuming that the distance follows the Haldane map function (Wu et al., 2007). EBlasso apparently cannot identify such highly correlated QTLs simultaneously. Borrowing the idea of EN (Zou and Hastie, 2005), we will apply a two-level hierarchical prior to β in (2) that will yield an equivalent EN prior for β. Then we will develop the EBEN algorithm that can handle correlated QTLs, and will be shown to outperform both EN and EBlasso.
Bayesian EN prior
The unknown parameters in model (2) are μ,  and β. Although our main concern is β, parameters μ and
and β. Although our main concern is β, parameters μ and  need to be estimated so that we can infer β. To this end, we assign a noninformative uniform prior to μ and
need to be estimated so that we can infer β. To this end, we assign a noninformative uniform prior to μ and  , that is, p(μ)∝1 and
, that is, p(μ)∝1 and  . Then we assume a two-level hierarchical model for β. Let us denote the elements of β as βj, j=1,2,···,k. At the first level, βj, j=1,2,···,k, follow independent normal distributions with mean zero and unknown variance
. Then we assume a two-level hierarchical model for β. Let us denote the elements of β as βj, j=1,2,···,k. At the first level, βj, j=1,2,···,k, follow independent normal distributions with mean zero and unknown variance  . Let us define
. Let us define  , j=1, 2, ···, k, as precision of the normal prior distribution, and let
, j=1, 2, ···, k, as precision of the normal prior distribution, and let  and α=[α1,α2, ···,αk]T. It turns out to be more convenient to estimate α than σ2. At the second level, we decompose αj as
and α=[α1,α2, ···,αk]T. It turns out to be more convenient to estimate α than σ2. At the second level, we decompose αj as  , j=1, 2, ···, k, where λ1⩾0 is a constant and
, j=1, 2, ···, k, where λ1⩾0 is a constant and  is a random variable whose distribution will be specified as follows. Defining
is a random variable whose distribution will be specified as follows. Defining  , we assign a generalized Gamma distribution to
, we assign a generalized Gamma distribution to  :
:

where c is a normalization constant, and λ2⩾0 is another constant.
The prior distribution (3) has two important properties. First, for λ1=0, it becomes an exponential distribution  with c=λ2, and the distribution of βj can be found to be the Laplace distribution
with c=λ2, and the distribution of βj can be found to be the Laplace distribution  , yielding the penalty used by Lasso (Tibshirani, 1996). Second, for given λ1>0, λ2⩾0 and
, yielding the penalty used by Lasso (Tibshirani, 1996). Second, for given λ1>0, λ2⩾0 and  ,
,  becomes a shifted Gamma distribution (Pal et al., 2005):
becomes a shifted Gamma distribution (Pal et al., 2005):

where a=1/2, b=λ2 and γ=−1/λ1, and the distribution of βj can be found to be  (see Appendix A for the proof), yielding the penalty used by EN (Zou and Hastie, 2005). Throughout the paper, we will refer to the regression model (2) with the two-level hierarchical prior as the BEN model. Note that when λ1=0, the prior distribution is the same as the normal-exponential (NE) prior of the EBlasso (EBlasso-NE) (Huang et al., 2013), thus the EBlasso-NE model is a special case of the BEN model.
(see Appendix A for the proof), yielding the penalty used by EN (Zou and Hastie, 2005). Throughout the paper, we will refer to the regression model (2) with the two-level hierarchical prior as the BEN model. Note that when λ1=0, the prior distribution is the same as the normal-exponential (NE) prior of the EBlasso (EBlasso-NE) (Huang et al., 2013), thus the EBlasso-NE model is a special case of the BEN model.
Let us define  and collect all parameters that need to be estimated as
and collect all parameters that need to be estimated as  . The joint posterior distribution of θ can be easily found and MCMC simulation can be employed to draw samples from the posterior distribution for each parameter (Robert and Casella, 2004). However, the fully Bayesian approach-based on MCMC sampling requires a prohibitive computational cost when the number of parameters 2k+4 becomes relatively large. Here, we adopt the same strategy used by EBlasso to develop an efficient empirical Bayesian algorithm to infer the BEN model.
. The joint posterior distribution of θ can be easily found and MCMC simulation can be employed to draw samples from the posterior distribution for each parameter (Robert and Casella, 2004). However, the fully Bayesian approach-based on MCMC sampling requires a prohibitive computational cost when the number of parameters 2k+4 becomes relatively large. Here, we adopt the same strategy used by EBlasso to develop an efficient empirical Bayesian algorithm to infer the BEN model.
Maximum a posteriori estimation of variance components
We will show that  can be estimated in closed-form, which will result in the efficient EBEN algorithm. The posterior distribution of parameters θ is given by:
can be estimated in closed-form, which will result in the efficient EBEN algorithm. The posterior distribution of parameters θ is given by:

The marginal posterior distribution of μ,  and
and  can be written as
can be written as  , from which the log marginal posterior distribution of
, from which the log marginal posterior distribution of  is derived as follows:
is derived as follows:

where  is the covariance matrix of y with a given
is the covariance matrix of y with a given  .
.
Let us define  . Then we can write
. Then we can write  in (6) as
in (6) as  , where
, where  does not depend on
does not depend on  and
and  is given by
is given by

with  and
and  . It is seen that (7) is similar to L(αj) of EBlasso-NE (Huang, et al., 2013, Equation (11)) except that λ1 appears in the denominators of the first two terms. Therefore, as shown in Appendix B,
. It is seen that (7) is similar to L(αj) of EBlasso-NE (Huang, et al., 2013, Equation (11)) except that λ1 appears in the denominators of the first two terms. Therefore, as shown in Appendix B,  has a unique global maximum and the optimal
has a unique global maximum and the optimal  maximizing
maximizing  is given by
is given by

where  , and
, and  . Of note, if
. Of note, if  , then
, then  , which is equivalent to βj=0.
, which is equivalent to βj=0.
EBEN algorithm and statistical significance test
Similar to the EBlasso algorithm, EBEN employs a coordinate ascent method to estimate unknown parameters  , μ and
, μ and  . After these parameters are estimated, the posterior distribution of β, which is a Gaussian distribution, can be found. Specifically, in each cycle of the coordinate ascent method,
. After these parameters are estimated, the posterior distribution of β, which is a Gaussian distribution, can be found. Specifically, in each cycle of the coordinate ascent method,  is estimated from (8) with all other parameters fixed, and μ and
is estimated from (8) with all other parameters fixed, and μ and  are estimated using Equations (15) and (16) in Cai et al. (2011), respectively. In the initial cycle, only one appropriately selected
are estimated using Equations (15) and (16) in Cai et al. (2011), respectively. In the initial cycle, only one appropriately selected  is finite (Cai et al., 2011), which corresponds to a model with only one variable xj. In the following cycles, a variable xl is added to the model if
is finite (Cai et al., 2011), which corresponds to a model with only one variable xj. In the following cycles, a variable xl is added to the model if  is finite, or is removed from the model if
is finite, or is removed from the model if  is infinite. The iterative process continues until convergence criterion is satisfied. Specifically, the following convergence criteria are applied: (i) no effect can be added to or deleted from the model, (ii) the change of
is infinite. The iterative process continues until convergence criterion is satisfied. Specifically, the following convergence criteria are applied: (i) no effect can be added to or deleted from the model, (ii) the change of  between two consecutive iterations,
between two consecutive iterations,  , is smaller than a pre-specified small value, and (iii) the Euclidean norm of the change of
, is smaller than a pre-specified small value, and (iii) the Euclidean norm of the change of  between two consecutive iterations,
between two consecutive iterations,  , is less than a pre-specified value. During the iteration, many
, is less than a pre-specified value. During the iteration, many  will be infinite, and the corresponding βjs are zero.
will be infinite, and the corresponding βjs are zero.
The EBEN algorithm can be obtained from the EBlasso algorithm (Cai et al., 2011) with the following two modifications: (i) replace αj with  and estimate
and estimate  from (8), and (ii) replace hyperparameters (a, b) in EBlasso with λ1 and λ2 and use cross validation (CV) to determine λ1 and λ2. A step-by-step description for the EBlasso algorithm is given in (Cai et al., 2011). The EBEN algorithm is provided in Appendix C.
from (8), and (ii) replace hyperparameters (a, b) in EBlasso with λ1 and λ2 and use cross validation (CV) to determine λ1 and λ2. A step-by-step description for the EBlasso algorithm is given in (Cai et al., 2011). The EBEN algorithm is provided in Appendix C.
The EBEN algorithm will select k′ (typically k′<<k) nonzero elements of β, which is denoted as a k′ × 1 vector β′, that corresponds to finite  . Let
. Let  be a k′ × 1 vector contain all finite
be a k′ × 1 vector contain all finite  . Given
. Given  , it is not difficult to show that the posterior distribution of β′ is a Gaussian distribution with mean
, it is not difficult to show that the posterior distribution of β′ is a Gaussian distribution with mean  and covariance
and covariance  , where
, where  is an n × k′ matrix that contains the columns of X corresponding to β′, and A is a diagonal matrix with
is an n × k′ matrix that contains the columns of X corresponding to β′, and A is a diagonal matrix with  on its diagonal. Note that given A,
on its diagonal. Note that given A,  is equivalent to the best linear unbiased prediction of β′ in the linear model with k′ random effects. For the jth element of β′,
is equivalent to the best linear unbiased prediction of β′ in the linear model with k′ random effects. For the jth element of β′, , the Bayesian approach needs to calculate the Bayesian factor to determine the significance of hypothesis H1:
, the Bayesian approach needs to calculate the Bayesian factor to determine the significance of hypothesis H1:  against hypothesis H0:
against hypothesis H0:  . However, the Bayesian factor is not easy to calculate. One way to overcome this problem is to employ the EBEN algorithm to select variables and then use the multisplit method (Meinshausen and Bühlmann, 2010) to determine the statistical significance of selected regression coefficients. However, the multisplit method is computationally demanding and its conservative approach to calculating P-values may reduce the power of detection. In this paper, we will use the following t-test to determine the significance of
. However, the Bayesian factor is not easy to calculate. One way to overcome this problem is to employ the EBEN algorithm to select variables and then use the multisplit method (Meinshausen and Bühlmann, 2010) to determine the statistical significance of selected regression coefficients. However, the multisplit method is computationally demanding and its conservative approach to calculating P-values may reduce the power of detection. In this paper, we will use the following t-test to determine the significance of  and compare its performance with that of the multisplit method. Because the standard deviation of
and compare its performance with that of the multisplit method. Because the standard deviation of  in the posterior distribution is
in the posterior distribution is  , where
, where  is the jth diagonal element of
is the jth diagonal element of  , we will use the t-statistics
, we will use the t-statistics  to test if
to test if  at 0.05 significance level. Essentially, we assume that the posterior distribution of
at 0.05 significance level. Essentially, we assume that the posterior distribution of  follows Student’s t-distribution and use the 0.95 credible interval to determine if
follows Student’s t-distribution and use the 0.95 credible interval to determine if  .
.
Cross validation
Two hyperparameters λ1⩾0 and λ2⩾0 need to be determined with CV. To facilitate CV, we define λ1 and λ2 in terms of other two parameters λ>0 and υ∈[0,1]: λ1=(1−υ)λ and λ2=υλ. Note that when υ=1, EBEN is equivalent to EBLasso-NE for a given pair of λ and υ. We perform fivefold CV and calculate the prediction error (Tibshirani, 1996)  , where is the predicted phenotype. We calculate
, where is the predicted phenotype. We calculate  , and chose a set of values for λ decreasing from λmax to 0.001 λmax in 20 even steps on the logarithmic scale. We vary υ from 1 to 0 at a step size of 0.05, and for each υ we repeat CV for all values of λ from λmax to 0.001 λmax. The pair of (υ, λ) that yields the smallest prediction error is chosen to be the optimal parameters, which are then used by EBEN to infer the model.
, and chose a set of values for λ decreasing from λmax to 0.001 λmax in 20 even steps on the logarithmic scale. We vary υ from 1 to 0 at a step size of 0.05, and for each υ we repeat CV for all values of λ from λmax to 0.001 λmax. The pair of (υ, λ) that yields the smallest prediction error is chosen to be the optimal parameters, which are then used by EBEN to infer the model.
Simulation setup and real data analysis
We simulated a population of an F2 family derived from the cross of two inbred lines with m=481 genetic markers which were evenly spaced on a large chromosome of 2400 cM (interval d=5 cM). The dummy variable for the three genotypes, A1A1, A1A2 and A2A2 of individual i at marker j was defined as xij=1, 0, −1, respectively. We assumed that QTLs were coincided with markers. If QTLs were not on markers, they may still be detected because correlation between a QTL and a nearby marker was high, although a slightly larger sample size may be needed to give the same power of detection.
We performed two sets of simulations based on the F2 population, each with 50 QTLs, whose effect sizes were randomly generated from a normal distribution with mean zero and variance equal to four. Environmental effects were not simulated. The true population mean was μ=100 and the residual variance was  . In the first set of simulations (SimI), 10 groups of two adjacent markers were selected randomly as QTLs; the minimum distance between any two groups of QTLs was 65 cM. The remaining 30 QTLs were selected randomly from the remaining markers. In the second set of simulations (SimII), 10 groups of five consecutive markers were randomly selected as 50 QTLs; the minimum distance between any two groups was 25 cM. For each set of simulations, 100 replicates were generated with sample sizes 200, 400, 600, 800 and 1000, and analyzed using EBEN, EBLasso-NEG (Cai et al., 2011) and EN (Zou and Hastie, 2005). Power of detection, FDR and power of detecting groups of QTLs of three methods were compared.
. In the first set of simulations (SimI), 10 groups of two adjacent markers were selected randomly as QTLs; the minimum distance between any two groups of QTLs was 65 cM. The remaining 30 QTLs were selected randomly from the remaining markers. In the second set of simulations (SimII), 10 groups of five consecutive markers were randomly selected as 50 QTLs; the minimum distance between any two groups was 25 cM. For each set of simulations, 100 replicates were generated with sample sizes 200, 400, 600, 800 and 1000, and analyzed using EBEN, EBLasso-NEG (Cai et al., 2011) and EN (Zou and Hastie, 2005). Power of detection, FDR and power of detecting groups of QTLs of three methods were compared.
We used a barley double haploid population published by Hayes et al. (1993) as an example to test our method. The dataset consisted of n=150 double haploid derived from the cross of two spring barley varieties, Morex and Steptoe. The total number of markers was q=495 distributed along seven pairs of chromosomes of the barley genome. The traits included three agronomic traits, grain yield, heading date and height, and five malting quality traits, lodging, grain protein, alpha amylase, diastatic power and malt extract. The marker intervals ranged from 0.6 to 23.3 cM, with median interval size 1.4 cM. With such high-density markers, correlations among markers were high. Genotype of the markers were encoded as +1 for genotype A (the Steptoe parent), −1 for genotype B (the Morex parent), and 0 for missing genotype. The total missing genotypes account for about 4.2% of all the genotypes.
Results
Estimated effects for one replicate in SimI
For a replicate of SimI shown in Table 1, we obtained the total phenotypic variance for the trait by

where cov(xj, xj′) is the covariance between xj and xj′ if j≠j′ or the variance of xj′ if j=j′, which can be estimated from the data. For this example, n=1000 samples were used. The total phenotypic variance was calculated from (9) to be  and the total genetic variance contributed by the main effects of the markers was calculated as 92.44. If we ignore the contributions from the covariance terms that are relatively small, the proportions of the phenotypic variance explained by a particular QTL effect j can be approximated by
and the total genetic variance contributed by the main effects of the markers was calculated as 92.44. If we ignore the contributions from the covariance terms that are relatively small, the proportions of the phenotypic variance explained by a particular QTL effect j can be approximated by

where var(xj) is the variance of Xj. In the simulated data, the proportion of contribution from an individual QTL varied from 0.01% to 6.61% as shown in Table 1.
The data were analyzed in R on a personal computer using EBEN, EN (Zou and Hastie, 2005) and EBLasso-NEG (Cai et al., 2011). We obtained the program glmnet (Friedman et al., 2010) that implements EN. CV for EBEN determined the optimal υ and λ as υ=0.95 and λ=0.0072. With the two values, EBEN identified 54 effects with a P-value ⩽0.05. We counted multiple identified effects that were within 20 cM distance to a true QTL as a true effect, and all effects with more than 20 cM distance to any true QTLs as false effects, resulted in 47 true effects and 3 false effects (Table 1). Simulated effects and QTLs identified by EBEN are visualized in Figure 1 (top).
EN has the same pair of parameters υ and λ as EBEN, and for each υ, λ is chosen from λmax to 0.001 λmax in 100 even steps on the logarithmic scale. CV gave the optimal values (υ, λ)=(0.95, 0.0734). Using these optimal values, EN identified 116 markers with nonzero regression coefficients. However, EN does not give a P-value for each estimated coefficient. If we regarded all 116 effects as QTLs, we would get a large number of false QTLs. To avoid this problem, we refitted an ordinary linear regression model with the 116 markers and calculated a P-value for each marker. Among those markers with a P-value ⩽0.05 in the refitted model, 37 markers corresponded to true-positive effects and 4 corresponded to false-positive effects were identified. The estimated sizes of 37 true effects and their standard deviations are listed along with all 50 true effects in Table 1, and QTLs identified are depicted in Figure 1 (bottom).
EBLasso-NEG (Cai et al., 2011) has two hyperparameters a and b controlling the degree of shrinkage, and CV chose the optimal values (a, b)=(−0.9, 1). Using the values, EBlasso-NEG identified 43 true- and 2 false-positive effects with a P-value ⩽0.05. The estimated sizes of true effects and their standard deviations are listed in Table 1, and QTLs identified are plotted in Figure 1 (middle).
Comparing the results of three algorithms, we observe that EBEN detected the most number of true effects, whereas three methods yielded similar number of false-positive effects. To see if the three algorithms can detect correlated effects, we highlight 10 groups that include neighboring markers in Table 1. Because the genetic markers were simulated with Haldane map function, the correlation between two neighboring markers is 0.9048, and the correlation between every other neighboring marker is 0.8187. It is seen that EBEN missed only markers 157 and 409 but detected them from other nearby markers. However, EN and EBlasso-NEG missed at least one QTL of 7 and 6 groups, respectively.
Results for SimI and SimII
The power of detection, FDR and power of detecting groups obtained from Sim I using EBEN, EBLasso and EN were plotted in Figure 2. As described in the Materials and Methods section, 10 groups of highly correlated QTLs are present in Sim I. When computing the power of detecting groups, a group was detected if all effects in the group were detected. From Figure 2, we observed that EBEN offered the highest power of detection and all three methods provided similar FDR; EBEN also had the highest power of detecting groups of QTLs as expected. Both EBEN and EBlasso-NEG outperformed EN. Taking sample size n=400 as an example, we see that the power of detection, FDR and power of detecting groups are 0.82, 0.11 and 0.64, respectively, for EBEN, 0.76, 0.11 and 0.48, respectively, for EBlasso-NEG, and 0.53 0.15, and 0.26, respectively, for EN.
In SimI, there were several groups with three effects because of random selection of QTL locations. However, more than 25 out of the 50 QTLs were not in any group, which means that none of its neighboring markers were also QTL (see Table 1 for an example). In SimII, all effects were within one of the groups. The power of detection, FDR and power of detecting groups of the three methods were plotted in Figure 3, which shows that EBEN performed much better than the other two methods in terms of power of detection whereas three methods yielded similar FDR. Again, taking sample size n=400 as an example, we see that the power of detection, FDR and power of detecting groups are 0.81, 0.10 and 0.35, respectively, for EBEN, 0.65, 0.12 and 0.14, respectively, for EBlasso-NEG, and 0.52, 0.16 and 0.05, respectively, for EN. Comparing the results of SimI and SimII, we observed that the performance of EBlasso and EN were degraded when the degree of grouping increased, whereas EBEN offered relatively stable power of detection and FDR.
As described in the Materials and Methods section, the multisplit method (Meinshausen et al., 2009) can be another choice for testing the significance of nonzero regression coefficients (Li and Sillanpää, 2012). To see the performance of the mulisplit method, we applied it to SimI and SimII with two sample sizes N=400 and N=600 and compared the power of detection, FDR and power of detecting groups of the multisplit method and the t-test, at a family-wise error rate of 0.05. The results are shown in Supplementary Figures S1 and S2 in the Supplementary Information. From Supplementary Figure S1 and S2, we observe that the t-test offered significantly higher power of detection than the multisplit method; its FDR was higher than the zero FDR of the multisplit method, but was still very low, less than 0.04.
Real data analysis
This dataset was used as an example for the application of EBEN in QTL mapping with high-density markers. We analyzed all eight traits but only presented results for three agronomic traits while leaving results for the five malting quality traits in the Supplementary Information.
In QTL mapping for grain yield, fivefold CV chose (υ, λ)=(0.35, 0.1710) for EBEN. With these values, EBEN identified 12 QTLs with a P-value ⩽0.05, which explained 57.93% of the total phenotypic variance (Table 2). Fivefold CV determined optimal parameters (υ, λ)=(0.65, 0.0354) for EN. Using the optimal values, EN identified 42 nonzero effects; after refitting the phenotype to the ordinary linear regression model with these 42 markers, six QTLs with a P-value ⩽0.05 were identified. The total phenotypic variance explained by six QTLs was 23.72%. Fivefold CV selected (a, b)=(0.01, 0.05) for EBlasso-NEG, with which six effects with a P-value ⩽0.05 were identified. These six effects explained 51.08% of the total phenotypic variance. The identified QTLs using the three methods are listed in Table 2.
In QTL mapping for heading date, EBEN identified 14 QTLs having a P-value ⩽0.05 with CV selected optimal parameters, and 93.87% of the total phenotypic variance were explained (Table 3). EN identified 59 nonzero effects; after refitting the phenotype to the ordinary linear regression model with these 59 markers, 11 QTLs with a P-value ⩽0.05 were identified. The total phenotypic variance explained by six QTLs was 70.28%. EBlasso-NEG identified eight effects with a P-value ⩽0.05, which explained 91.13% of the total phenotypic variance. The identified QTLs using the three methods are listed in Table 3.
In QTL mapping for the height of barley, using CV-selected optimal parameter values, EBEN identified 16 QTLs with a P-value ⩽0.05, which explained 93.29% of the total phenotypic variance (Table 4); EN identified 52 nonzero effects, with which 9 QTLs with a P-value ⩽0.05 were identified by refitting the phenotype to the ordinary linear regression model, and 44.30% of the total phenotypic variance were explained; EBlasso-NEG identified 9 effects with a P-value ⩽0.05, which explained 87.67% of the total phenotypic variance. The identified QTLs using the three methods are listed in Table 4.
Apparently, EBEN detected more effects than EN and EBlasso-NEG, although it also missed some of the effects detected by EN and EBlasso-NEG. Moreover, effects detected by EBEN explained more phenotypic variance than those detected by EN or EBlasso-NEG. Particularly, EBEN detected markers 403 and 406 for grain yield, 96, 97 and 98 for heading date, 74 and 75 for height, which were 4.1, 0.7 and 0.8 cM apart, respectively, and were highly correlated, but both EN and EBlasso-NEG were able to detect only one effect for each group. Results for other five traits are listed in Supplementary Tables S1–S5, which also shows that EBEN detected more effects, and these effects explained more phenotypic variance for all five traits compared with EN and EBlasso-NEG.
In computer simulations, it was observed that the computational time for the three methods was mainly determined by the number of nonzero markers in the inferred QTL model, and that EBEN had a speed similar to EN and EBlasso-NEG. In the analysis of the grain yield with the optimal hyperparameters chosen by CV, the computational time was 0.10 s for EBEN, 0.05 s for EN and 0.06 s for EBlasso-NEG. All computations were performed on a personal computer with a 2.6 GHz Intel Core 2 CPU and 4 Gb memory running Windows7.
Discussion
We have developed a novel EBEN algorithm for multiple QTL mapping. Simulation results demonstrated that our EBEN outperformed two other algorithms EN (Zou and Hastie, 2005) and EBlasso-NEG (Cai et al., 2011). Particularly, EBEN could detect more correlated effects than other two algorithms. When applied to a real barley dataset, EBEN was able to detect more QTLs and explain higher proportion of phenotypic variance than other two algorithms.
Our EBEN model essentially uses the same prior for regression coefficients as the one used by EN. For model inference, our EBEN first estimates the covariance of regression coefficients. During the estimation process, many coefficients are shrunk to zero if the corresponding variance is zero. After the covariance is obtained, the nonzero coefficients were estimated as a Gaussian random vector with an estimated mean and an estimated covariance. On the other hand, EN directly estimates the nonzero regression coefficients without estimating the covariance. Because our EBEN yields not only a point estimate of regression coefficients but also an estimate of their covariance, this gives more information than the point estimate of EN, which may help to improve performance. Our EBEN model and the Bayesian EN model in Li and Lin (2010) have some similarities and differences. The model of Li and Lin assumes the following prior:  ,
,  ,
,  , where TG(·) is a truncated Gamma distribution. Unlike the model of Li and Lin, where prior of βj is conditioned on the noise variance
, where TG(·) is a truncated Gamma distribution. Unlike the model of Li and Lin, where prior of βj is conditioned on the noise variance  , the prior of βj in our BEN model is independent of
, the prior of βj in our BEN model is independent of  , because only a point estimate of
, because only a point estimate of  is needed in our model inference. In the model of Li and Lin (2010), if we define
is needed in our model inference. In the model of Li and Lin (2010), if we define  , then
, then  , this decomposition of
, this decomposition of  is similar to that in our BEN model:
is similar to that in our BEN model:  . Because τj follows a truncated Gamma distribution with a support of (1, ∞),
. Because τj follows a truncated Gamma distribution with a support of (1, ∞),  obeys a shifted Gamma distribution similar to the prior for
obeys a shifted Gamma distribution similar to the prior for  in our BEN model. We assigned a uniform prior to
in our BEN model. We assigned a uniform prior to  , whereas Li and Lin (2010) used the Jeffrey’s prior for
, whereas Li and Lin (2010) used the Jeffrey’s prior for  . Li and Lin (2010) employed MCMC for model inference, which is computationally demanding, whereas our EBEN algorithm does not rely on MCMC and is more efficient.
. Li and Lin (2010) employed MCMC for model inference, which is computationally demanding, whereas our EBEN algorithm does not rely on MCMC and is more efficient.
Simulations demonstrated that our EBEN algorithm improves performance in terms of power of detection and FDR by taking into account the possible correlations among QTLs, which agrees with previous observations (Gianola et al., 2003). Several methods for predicting genetic values incorporate the spatial correlations among markers. Yang and Tempelman (2012) included a first-order antedependence correlation structure for regression coefficients β into their Bayesian hierarchical mixed effects model so that βj depends on βj−1, 2⩽j⩽k, resulted in increased accuracy in predicting genetic values. Shen et al. (2011) incorporated a specific correlation structure in their smoothed double hierarchical generalized linear model, and a spatial correlation parameter was introduced to control correlation between two markers. Although our EBEN exploits the possible correlations among QTLs, unlike those of Shen et al. (2011), Yang and Tempelman (2012), our EBEN does not specify a correlation structure for markers in the QTL model. Therefore, our EBEN is more robust, because a mis-specified correlation structure may significantly degrade performance. Our EBEN can shrink most variables in the QTL model to zero, yielding a sparse QTL model, which significantly decreases FDR without sacrificing the power of detection; whereas the method of Shen et al. (2011) does not employ the shrinkage technique, and it is not clear if the method of Yang and Tempelman (2012) can shrink variables in the QTL model to zero. Although performance of predicting genetic values may not degrade without using the shrinkage technique or an appropriate variable selection method to identify QTLs, shrinkage is very important to the performance of QTL mapping.
The EBEN algorithm inherits the efficiency of the EBlasso algorithm, because it is modified from the later, although the BEN model used by the EBEN algorithm is different from the Bayesian Lasso model used by the EBlasso algorithm. Our simulations (Cai et al., 2011; Huang et al., 2013) have shown that EBlasso outperformed a number of other competing algorithms in terms of detection power and FDR, and it offered a speed comparable to Lasso implemented with glmnet (Friedman et al., 2010) but faster than other algorithms compared. EBEN improves the power of detection relative to EBlasso by detecting more correlated effects as shown in the simulation. However, in real data analysis, we observed that although EBEN detected more effects, it also missed several effects detected by EBlasso. One explanation is that EBEN outputs smaller estimates for the absolute amplitudes of correlated effects than EBlasso. A similar effect was observed for EN (Zou and Hastie, 2005) compared with Lasso. This may reduce the significance of the estimated effects. Therefore, when analyzing real data, we may apply both EBEN and EBlasso and take QTLs identified by either algorithm.
The EBEN algorithm was developed for quantitative traits, it can also be easily extended to QTL mapping with a logistic regression model for binary traits, following the derivations in (Huang et al., 2013). Moreover, thanks to the regression model, it is straightforward to incorporate other covariates and maker interactions into the EBEN model. Recently, EBlasso has been applied to whole-genome QTL mapping (Huang et al., 2014b) and pathway-based genome-wide association study (Huang et al., 2014a), where linear regression models with millions of variables were inferred with EBLasso. Because EBEN inherits the computational efficiency of EBlasso, it can also be applied to both whole-genome QTL mapping and genome-wide association study. In conclusion, EBEN algorithm provides a useful tool for inference of high-dimensional sparse regression model in multiple QTL mapping and other applications.
Data archiving
The genotype and phenotype data for simulation settings SimI and SimII are available at Dryad (DOI: 10.5061/dryad.jf142).
References
Andrews DF, Mallows CL . (1974). Scale mixtures of normal distributions. J R Stat Soc Series B Stat Methodol 36: 99–102.
Bogdan M, Frommlet F, Biecek P, Cheng R, Ghosh JK, Doerge RW . (2008). Extending the modified Bayesian information criterion (mBIC) to dense markers and multiple interval mapping. Biometrics 64: 1162–1169.
Cai X, Huang A, Xu S . (2011). Fast empirical Bayesian LASSO for multiple quantitative trait locus mapping. BMC Bioinformatics 12: 211.
Cockerham CC . (1954). An extension of the concept of partitioning hereditary variance for analysis of covariances among relatives when epistasis is present. Genetics 39: 859–882.
Friedman J, Hastie T, Tibshirani R . (2010). Regularization paths for generalized linear models via coordinate descent. J Stat Softw 33: 1–22.
Gianola D, Perez-Enciso M, Toro MA . (2003). On marker-assisted prediction of genetic value: beyond the ridge. Genetics 163: 347–365.
Hayes P, Liu B, Knapp S, Chen F, Jones B, Blake T et al. (1993). Quantitative trait locus effects and environmental interaction in a sample of North American barley germ plasm. Theor Appl Genet 87: 392–401.
Hoti F, Sillanpää MJ . (2006). Bayesian mapping of genotype x expression interactions in quantitative and qualitative traits. Heredity 97: 4–18.
Huang A, Martin E, Vance J, Cai X . (2014a). Detecting genetic interactions in pathway-based genome-wide association studies. Genet Epidemiol 38: 300–309.
Huang A, Xu S, Cai X . (2013). Empirical Bayesian LASSO-logistic regression for multiple binary trait locus mapping. BMC Genet 14: 5.
Huang A, Xu S, Cai X . (2014b). Whole-genome quantitative trait locus mapping reveals major role of epistasis on yield of rice. PLoS ONE 9: e87330.
Huang H, Eversley CD, Threadgill DW, Zou F . (2007). Bayesian multiple quantitative trait loci mapping for complex traits using markers of the entire genome. Genetics 176: 2529–2540.
Li Q, Lin N . (2010). The Bayesian elastic net. Bayesian Anal 5: 151–170.
Li S, Lu Q, Fu W, Romero R, Cui Y . (2009). A regularized regression approach for dissecting genetic conflicts that increase disease risk in pregnancy. Stat Appl Genet Mol Biol 8: 1–28.
Li Z, Sillanpää M . (2012). Overview of LASSO-related penalized regression methods for quantitative trait mapping and genomic selection. Theor Appl Genet 125: 419–435.
Meinshausen N, Bühlmann P . (2010). Stability selection. J R Stat Soc Series B Stat Methodol 72: 417–473.
Meinshausen N, Meier L, Bühlmann P . (2009). P-values for high-dimensional regression. J Am Stat Assoc 104: 713–725.
O'Hara RB, Sillanpaa MJ . (2009). A review of Bayesain variable selection methods: what, how and which. Bayesian Anal 4: 8–118.
Pal N, Jin C, Lim WK . (2005) Handbook of Exponential and Related Distributions for Engineers and Scientists. CRC Press: New York.
Park T, Casella G . (2008). The Bayesian lasso. J Am Stat Assoc 103: 681–686.
Robert CR, Casella G . (2004) Monte Carlo statistical methods 2 edn. Springer: New York.
Schwarz G . (1978). Estimating the dimension of a model. Ann Stat 6: 461–464.
Shen X, Ronnegard L, Carlborg O . (2011). Hierarchical likelihood opens a new way of estimating genetic values using genome-wide dense marker maps. BMC Proceedings 5 (Suppl 3): S14.
Tibshirani R . (1996). Regression shrinkage and selection via the lasso. J R Stat Soc Series B Stat Methodol 58: 267–288.
Wang H, Zhang YM, Li X, Masinde GL, Mohan S, Baylink DJ et al. (2005). Bayesian shrinkage estimation of quantitative trait loci parameters. Genetics 170: 465–480.
Wu R, Ma CX, Casella G . (2007) Statistical Genetics of Quantitative Traits: Linkage, Maps, and QTL. Springer: New York.
Xu S . (2003). Estimating polygenic effects using markers of the entire genome. Genetics 163: 789–801.
Xu S . (2007). An empirical Bayes method for estimating epistatic effects of quantitative trait loci. Biometrics 63: 513–521.
Yang W, Tempelman RJ . (2012). A Bayesian antedependence model for whole genome prediction. Genetics 190: 1491–1501.
Yi N, Xu S . (2008). Bayesian LASSO for quantitative trait loci mapping. Genetics 179: 1045–1055.
Yu J, Zhang Z, Zhu C, Tabanao DA, Pressoir G, Tuinstra MR et al. (2009). Simulation appraisal of the adequacy of number of background markers for relationship estimation in association mapping. Plant Gen 2: 63–77.
Zou H, Hastie T . (2005). Regularization and variable selection via the elastic net. J R Stat Soc Series B Stat Methodol 67: 301–320.
Acknowledgements
This work was supported by the National Science Foundation [NSF CAREER Award no. 0746882 to XC] and by the Agriculture and Food Research Initiative (AFRI) of the USDA National Institute of Food and Agriculture under the Plant Genome, Genetics and Breeding Program [2007-35300-18285 to SX].
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on Heredity website
Appendices
Appendix A
Proof of the EN prior distribution
The joint prior distribution for βj and  can be written as:
can be written as:

where  is a normal distribution:
is a normal distribution:  and
and  is a generalized Gamma distribution:
is a generalized Gamma distribution:  with C being a normalization constant. The marginal prior distribution of βj can be found as
with C being a normalization constant. The marginal prior distribution of βj can be found as

Using the result in Andrews and Mallows (1974), the integral can be found in a closed-form for λ2>0, and p(βj|λ1, λ2) is simplified as  , which is the EN prior distribution.
, which is the EN prior distribution.
Appendix B
Derivation of equation (8)
Note that  ,
,  , and the derivative of
, and the derivative of  is given by:
is given by:

Let us write the numerator of the derivative as  , and define
, and define  . Because λ2>0, we have Δ⩾0, which implies that
. Because λ2>0, we have Δ⩾0, which implies that  have two roots:
have two roots:  and
and  . Next let us consider the following three cases:
. Next let us consider the following three cases:
Case 1: 
We have r1<0 and r2<0 because sj>0 and λ2>0. Therefore,  for
for  and
and  is an increasing function of
is an increasing function of  . This implies that
. This implies that  is maximized at
is maximized at  .
.
Case 2: 
In this case, we have  . It is clear that
. It is clear that  for
for  . Hence
. Hence  and
and  is an increasing function of
is an increasing function of  . Then
. Then  is maximized at
is maximized at  .
.
Case 3: 
We have r1>0 and r2<0. Therefore,  for
for  ,
,  for
for  , and
, and  for
for  . This implies that
. This implies that  is maximized at
is maximized at  and
and  because
because  .
.
Summarizing the results in three cases, we obtain  given in (8).
given in (8).
Appendix C
EBEN algorithm
-
1
Initialize parameters: choose υ∈[0,1] and λ>0, calculate μ=1Ty/n, = y −μ and set
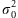 to be a small number, e.g., 0.1 × T/n.
to be a small number, e.g., 0.1 × T/n. -
2
Initialize the model: Find
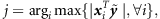 and calculate αj from (8); set all other αj′, j′≠j to be ∞ and
and calculate αj from (8); set all other αj′, j′≠j to be ∞ and  .
. -
3
Calculate Σ, sj and qj, ∀j.
-
4
Update the model.Apply the EBlasso algorithm (Cai et al., 2011) to update A with
 obtained from (8). If the global convergence criterion is not satisfied, go to step 4.
obtained from (8). If the global convergence criterion is not satisfied, go to step 4. -
5
Output
 and covariance
and covariance  .
.
Rights and permissions
About this article
Cite this article
Huang, A., Xu, S. & Cai, X. Empirical Bayesian elastic net for multiple quantitative trait locus mapping. Heredity 114, 107–115 (2015). https://doi.org/10.1038/hdy.2014.79
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2014.79
This article is cited by
-
MVQTLCIM: composite interval mapping of multivariate traits in a hybrid F1 population of outbred species
BMC Bioinformatics (2017)
-
Epistasis analysis of microRNAs on pathological stages in colon cancer based on an Empirical Bayesian Elastic Net method
BMC Genomics (2017)
-
Genetic dissection of heterosis using epistatic association mapping in a partial NCII mating design
Scientific Reports (2015)
-
An Integrated Approach to Empirical Bayesian Whole Genome Prediction Modeling
Journal of Agricultural, Biological, and Environmental Statistics (2015)






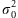 to be a small number, e.g., 0.1 × T/n.
to be a small number, e.g., 0.1 × T/n.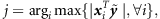 and calculate αj from (8); set all other αj′, j′≠j to be ∞ and
and calculate αj from (8); set all other αj′, j′≠j to be ∞ and  .
. obtained from (8). If the global convergence criterion is not satisfied, go to step 4.
obtained from (8). If the global convergence criterion is not satisfied, go to step 4. and covariance
and covariance  .
.