Abstract
A quantum processor can be used to exploit quantum mechanics to find the prime factors of composite numbers1. Compiled versions of Shor’s algorithm and Gauss sum factorizations have been demonstrated on ensemble quantum systems2, photonic systems3,4,5,6 and trapped ions7. Although proposed8, these algorithms have yet to be shown using solid-state quantum bits. Using a number of recent qubit control and hardware advances9,10,11,12,13,14,15,16, here we demonstrate a nine-quantum-element solid-state quantum processor and show three experiments to highlight its capabilities. We begin by characterizing the device with spectroscopy. Next, we produce coherent interactions between five qubits and verify bi- and tripartite entanglement through quantum state tomography10,14,17,18. In the final experiment, we run a three-qubit compiled version of Shor’s algorithm to factor the number 15, and successfully find the prime factors 48% of the time. Improvements in the superconducting qubit coherence times and more complex circuits should provide the resources necessary to factor larger composite numbers and run more intricate quantum algorithms.
Similar content being viewed by others
Main
In this experiment, we scaled up from an architecture initially implemented with two qubits and three resonators16 to a nine-element quantum processor capable of realizing rapid entanglement and a compiled version of Shor’s algorithm. The device is composed of four phase qubits and five superconducting co-planar waveguide (CPW) resonators, where the resonators are used as qubits by accessing only the two lowest levels. Four of the five CPWs can be used as quantum memory elements as in ref. 16 and the fifth can be used to mediate entangling operations.
The quantum processor can create entanglement and execute quantum algorithms19,20 with high-fidelity single-qubit gates21,22 (X, Y, Z and H) combined with swap and controlled-phase (Cϕ) gates15,16,23, where one qubit interacts with a resonator at a time. The quantum processor can also use fast-entangling logic by bringing all participating qubits on resonance with the resonator at the same time to generate simultaneous entanglement24. At present, this combination of entangling capabilities has not been demonstrated on a single device. Previous examples have shown spectroscopic evidence of the increased coupling for up to three qubits coupled to a resonator17, as well as coherent interactions between two and three qubits with a resonator14, although these lacked tomographic evidence of entanglement.
Here we show coherent interactions for up to four qubits with a resonator and verify genuine bi- and tripartite entanglement including Bell11 and |W〉 states12 with quantum state tomography (QST). This quantum processor has the further advantage of creating entanglement at a rate more than twice that of previous demonstrations12,14.
In addition to these characterizations, we chose to implement a compiled version of Shor’s algorithm25,26, in part for its historical relevance19 and in part because this algorithm involves the challenge of combining both single- and coupled-qubit gates in a meaningful sequence. We constructed the full factoring sequence by first performing automatic calibration of the individual gates and then combined them, without additional tuning, so as to factor the composite number  with co-prime a = 4, (where
with co-prime a = 4, (where  and the greatest common divisor between a and
and the greatest common divisor between a and  is 1). We also checked for entanglement at three points in the algorithm using QST.
is 1). We also checked for entanglement at three points in the algorithm using QST.
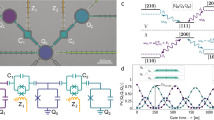
Figure 1a shows a micrograph of the quantum processor, made on a sapphire substrate using Al/AlOx/Al Josephson junctions. Figure 1b shows a complete schematic of the device. Each qubit Qi is individually controlled using a bias coil that carries d.c., radiofrequency and gigahertz pulses to adjust the qubit frequency and to pulse microwaves for manipulating and measuring the qubit state. Each qubit’s frequency can be adjusted over an operating range of ∼ 2 GHz, allowing us to couple each qubit to the other quantum elements on the chip. Each Qi is connected to a memory resonator Mi, as well as the bus B, through interdigitated capacitors. Although the coupling capacitors are fixed, Fig. 1c illustrates how the effective interaction can be controlled by tuning the qubits into or near resonance with the coupling bus (coupling on) or detuning Qi to fB±500 MHz (coupling off)27.
a, Photomicrograph of the sample, fabricated with aluminium (coloured) on sapphire substrate (dark). b, Schematic of the quantum processor. Each phase qubit Qi is capacitively coupled to the central half-wavelength bus resonator B and a quarter-wavelength memory resonator Mi. The control lines carry gigahertz microwave pulses to produce single-qubit operations. Each Qi is coupled to a superconducting quantum interference device (SQUID) for single-shot readout. c, Illustration of quantum processor operation. By applying pulses on each control line, each qubit frequency is tuned in and out of resonance with B (M) to perform entangling (memory) operations. d, Swap spectroscopy16 for all four qubits. Qubit excited state |e〉 probability Pe (colour scale) versus frequency (vertical axis) and interaction time Δτ. The centres of the chevron patterns gives the frequencies of the resonators B, M1–M4, f = 6.1,6.8,7.2,7.1,6.9 GHz, respectively. The oscillation periods give the coupling strengths between Qi and B (Mi), which are all  (
( ).
).
The quantum processor is mounted in a superconducting aluminium sample holder and cooled in a dilution refrigerator to ∼ 25 mK. Qubit operation and calibration are similar to previous works10,11,12,15,16, with the addition of an automated calibration process28. As shown in Fig. 1d, we used swap spectroscopy16 to calibrate all nine of the engineered quantum elements on the quantum processor, the four phase qubits (Q1–Q4), the four quarter-wave CPW quantum-memory resonators (M1–M4) and one half-wave CPW bus resonator (B). The coupling strengths between Qi and B (Mi) were measured to be within 5% (10%) of the design values.
The qubit–resonator interaction can be described by the Jaynes–Cummings model Hamiltonian29  , where gi is the coupling strength between the bus resonator B and the qubit Qi, a† and a are, respectively, the photon creation and annihilation operators for the resonator, σi+ and σi− are, respectively, the qubit Qi raising and lowering operators and ℏ = h/2π. The dynamics during the interaction between the i = {1,2,3,4} qubits and the bus resonator are shown in Fig. 1c and Fig. 2a,b,c respectively.
, where gi is the coupling strength between the bus resonator B and the qubit Qi, a† and a are, respectively, the photon creation and annihilation operators for the resonator, σi+ and σi− are, respectively, the qubit Qi raising and lowering operators and ℏ = h/2π. The dynamics during the interaction between the i = {1,2,3,4} qubits and the bus resonator are shown in Fig. 1c and Fig. 2a,b,c respectively.
a–c, The measured state occupation probabilities (colour) and Pb (black) for increasing number of participating qubits N = {2,3,4} versus interaction time Δτ. In all cases, B is first prepared in the n = 1 Fock state10 and the participating qubits are then tuned on resonance with B for the interaction time Δτ. The single excitation begins in B, spreads to the participating qubits and then returns to B. These coherent oscillations continue for a time Δτ and increase in frequency with each additional qubit. d, Oscillation frequency of Pb for increasing numbers of participating qubits. The error bars indicate the −3 dB point of the Fourier transformed Pb data. The inset schematics illustrate which qubits participate. The coupling strength increases as  , plotted as a black line fit to the data, with
, plotted as a black line fit to the data, with  . e,f, The real part of the reconstructed density matrices from QST. e, Bell singlet
. e,f, The real part of the reconstructed density matrices from QST. e, Bell singlet  with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.89±0.01 and EOF = 0.70. f, Three-qubit
with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.89±0.01 and EOF = 0.70. f, Three-qubit  with fidelity FW = 〈W|ρW|W〉 = 0.69±0.01. The measured imaginary parts (not shown) are found to be small, with
with fidelity FW = 〈W|ρW|W〉 = 0.69±0.01. The measured imaginary parts (not shown) are found to be small, with  (e) and
(e) and  (f), as expected theoretically.
(f), as expected theoretically.
For these interactions the qubits Q1–Q4 are initialized in the ground state |g g g g〉 and tuned off-resonance from B at an idle frequency f∼6.6 GHz. Q1 is prepared in the excited state |e〉 by a π-pulse. B is then pumped into the first Fock state n = 1 by tuning Q1 on resonance (f∼6.1 GHz) for a duration 1/2g1 = τ∼9 ns, long enough to complete an iSWAP operation between Q1 and B,  (ref. 10).
(ref. 10).
The participating qubits are then tuned on resonance (f∼6.1 GHz) and left to interact with B for an interaction time Δτ. Figure 2a–c shows the probability of measuring the participating qubits in the excited state, and the probability Pb of B being in the n = 1 Fock state, versus Δτ. At the beginning of the interaction the excitation is initially concentrated in B (Pb maximum) then spreads evenly between the participating qubits (Pb minimum) and finally returns back to B, continuing as a coherent oscillation during this interaction time.
When the qubits are simultaneously tuned on resonance with B they interact with an effective coupling strength  that scales with the number N of qubits as
that scales with the number N of qubits as  (ref. 17), analogous to a single qubit coupled to a resonator in an n-photon Fock state10. For N qubits,
(ref. 17), analogous to a single qubit coupled to a resonator in an n-photon Fock state10. For N qubits,  , where
, where  . The oscillation frequency of Pb for each of the four cases i = {1,2,3,4} is shown in Fig. 2 d. These results are similar to those of refs 17, 30, but with a larger number N of qubits interacting with the resonator, we can confirm the
. The oscillation frequency of Pb for each of the four cases i = {1,2,3,4} is shown in Fig. 2 d. These results are similar to those of refs 17, 30, but with a larger number N of qubits interacting with the resonator, we can confirm the  scaling of the coupling strength with N. From these data we find a mean value of
scaling of the coupling strength with N. From these data we find a mean value of  .
.
By tuning the qubits on resonance for a specific interaction time τ, corresponding to the first minimum of Pb in Fig. 2a,b we can generate Bell singlets  and |W〉 states
and |W〉 states  . Stopping the interaction at this time (τBell = 6.5 ns and τW = 5.1 ns) leaves the single excitation evenly distributed among the participating qubits and places the qubits in the desired equal superposition state similar to the protocol in ref. 14. We are able to further analyse these states using full QST. Figure 2e,f shows the reconstructed density matrices from this analysis18. The Bell singlet is formed with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.89±0.01 and entanglement of formation31 EOF = 0.70. The three-qubit |W〉state is formed with fidelity FW = 〈W|ρW|W〉 = 0.69±0.01, which satisfies the entanglement witness inequality FW>2/3 for three-qubit entanglement32. Generating either of these classes of entangled states (bi- and tripartite) requires only a single entangling operation that is short relative to the characteristic time for two-qubit gates (tg∼50 ns). This entanglement protocol has the further advantage that it can be scaled to an arbitrary number of qubits.
. Stopping the interaction at this time (τBell = 6.5 ns and τW = 5.1 ns) leaves the single excitation evenly distributed among the participating qubits and places the qubits in the desired equal superposition state similar to the protocol in ref. 14. We are able to further analyse these states using full QST. Figure 2e,f shows the reconstructed density matrices from this analysis18. The Bell singlet is formed with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.89±0.01 and entanglement of formation31 EOF = 0.70. The three-qubit |W〉state is formed with fidelity FW = 〈W|ρW|W〉 = 0.69±0.01, which satisfies the entanglement witness inequality FW>2/3 for three-qubit entanglement32. Generating either of these classes of entangled states (bi- and tripartite) requires only a single entangling operation that is short relative to the characteristic time for two-qubit gates (tg∼50 ns). This entanglement protocol has the further advantage that it can be scaled to an arbitrary number of qubits.
The quantum circuit for the compiled version of Shor’s algorithm is shown in Fig. 3a for factoring the number  with a = 4 co-prime25,26, which returns the period r = 2 (10 in binary) with a theoretical success rate of 50%. Although the success of the algorithm hinges on quantum entanglement, the final output is ideally a completely mixed state, σm = (1/2)(|0〉〈0|+|1〉〈1|). Therefore, measuring only the raw probabilities of the output register does not reveal the underlying quantum entanglement necessary for the success of the computation. Thus, we perform a runtime analysis with QST at the three points identified in Fig. 3b, in addition to recording the raw probabilities of the output register.
with a = 4 co-prime25,26, which returns the period r = 2 (10 in binary) with a theoretical success rate of 50%. Although the success of the algorithm hinges on quantum entanglement, the final output is ideally a completely mixed state, σm = (1/2)(|0〉〈0|+|1〉〈1|). Therefore, measuring only the raw probabilities of the output register does not reveal the underlying quantum entanglement necessary for the success of the computation. Thus, we perform a runtime analysis with QST at the three points identified in Fig. 3b, in addition to recording the raw probabilities of the output register.
a, Four-qubit circuit to factor  , with co-prime a = 4. The three steps in the algorithm are initialization (Init), modular exponentiation and the quantum Fourier transform, which computes
, with co-prime a = 4. The three steps in the algorithm are initialization (Init), modular exponentiation and the quantum Fourier transform, which computes  and returns the period r = 2. b, Recompiled three-qubit version of Shor’s algorithm. The redundant qubit Q1 is removed by noting that H H = I. Circuits a and b are equivalent for this specific case. The three steps of the runtime analysis are labelled 1,2 and 3. c, CNOT gates are realized using an equivalent CZ circuit. d, Step 1: Bell singlet between Q2 and Q3 with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.75±0.01 and EOF = 0.43. e, Step 2: Three-qubit
and returns the period r = 2. b, Recompiled three-qubit version of Shor’s algorithm. The redundant qubit Q1 is removed by noting that H H = I. Circuits a and b are equivalent for this specific case. The three steps of the runtime analysis are labelled 1,2 and 3. c, CNOT gates are realized using an equivalent CZ circuit. d, Step 1: Bell singlet between Q2 and Q3 with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.75±0.01 and EOF = 0.43. e, Step 2: Three-qubit  between Q2, Q3 and Q4 with fidelity FGHZ = 〈GHZ|ρGHZ|GHZ〉 = 0.59±0.01. f, Step 3: QST after running the complete algorithm. The three-qubit |GHZ〉 is rotated into |ψ3〉 = H2|GHZ〉 = (|g g g〉+|e g g〉+|g e e〉−|e e e〉)/2 with fidelity F = 0.55. g,h, The density matrix of the single-qubit output register Q2 formed by: tracing-out Q3 and Q4 from f (g), and directly measuring Q2 with QST (h), both with
between Q2, Q3 and Q4 with fidelity FGHZ = 〈GHZ|ρGHZ|GHZ〉 = 0.59±0.01. f, Step 3: QST after running the complete algorithm. The three-qubit |GHZ〉 is rotated into |ψ3〉 = H2|GHZ〉 = (|g g g〉+|e g g〉+|g e e〉−|e e e〉)/2 with fidelity F = 0.55. g,h, The density matrix of the single-qubit output register Q2 formed by: tracing-out Q3 and Q4 from f (g), and directly measuring Q2 with QST (h), both with  and Sl = 0.78. From 1.5×105 direct measurements, the output register returns the period r = 2, with probability 0.483±0.003, yielding the prime factors 3 and 5. i, The density matrix of the single-qubit output register without entangling gates, H2H2|g〉 = I|g〉. Ideally this calibration algorithm returns r = 0 100% of the time. Compared with the single quantum state |ψout〉 = |g〉, the fidelity Fcal = 〈ψg|ρcal|ψg〉 = 0.83±0.01, which is less than unity owing to the energy relaxation.
and Sl = 0.78. From 1.5×105 direct measurements, the output register returns the period r = 2, with probability 0.483±0.003, yielding the prime factors 3 and 5. i, The density matrix of the single-qubit output register without entangling gates, H2H2|g〉 = I|g〉. Ideally this calibration algorithm returns r = 0 100% of the time. Compared with the single quantum state |ψout〉 = |g〉, the fidelity Fcal = 〈ψg|ρcal|ψg〉 = 0.83±0.01, which is less than unity owing to the energy relaxation.
The first breakpoint in the algorithm verifies the existence of bipartite entanglement. A Bell singlet |ψs〉 is formed after a Hadamard gate22 (H) on Q2 and a controlled-NOT (CNOT; refs 15, 16) between Q2 and Q3. As illustrated in Fig. 3c, the CNOT gates are processed by inserting a controlled-Z (CZ) between two H gates on the target qubit. The CZ is realized as in ref. 16 by bringing the target qubit  transition on resonance with B to execute an (iSWAP)2. The target qubit acquires a phase shift of π conditioned on the control qubit. Figure 3d is the real part of the density matrix reconstructed from QST on |ψs〉. The singlet is formed with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.75±0.01 (
transition on resonance with B to execute an (iSWAP)2. The target qubit acquires a phase shift of π conditioned on the control qubit. Figure 3d is the real part of the density matrix reconstructed from QST on |ψs〉. The singlet is formed with fidelity FBell = 〈ψs|ρBell|ψs〉 = 0.75±0.01 ( not shown) and EOF = 0.43. The primary cause of the reduced fidelites were energy relaxation and dephasing of the qubits, with characteristic times of T1∼400 ns and T2∼200 ns, respectively, for all four qubits and T1∼3 μs for the bus resonator. Measurement fidelities for |g〉 and |e〉 for the four qubits are M1,g = 0.9523, M1,e = 0.8902, M2,g = 0.9596, M2,e = 0.9049, M3,g = 0.9490, M3,e = 0.9365, M4,g = 0.9579 and M4,e = 0.8323. For all reported QST fidelities, measurement errors have been subtracted.
not shown) and EOF = 0.43. The primary cause of the reduced fidelites were energy relaxation and dephasing of the qubits, with characteristic times of T1∼400 ns and T2∼200 ns, respectively, for all four qubits and T1∼3 μs for the bus resonator. Measurement fidelities for |g〉 and |e〉 for the four qubits are M1,g = 0.9523, M1,e = 0.8902, M2,g = 0.9596, M2,e = 0.9049, M3,g = 0.9490, M3,e = 0.9365, M4,g = 0.9579 and M4,e = 0.8323. For all reported QST fidelities, measurement errors have been subtracted.
The next breakpoint in the algorithm is after the second CNOT gate between Q2 and Q4 to check for tripartite entanglement. At this point a three-qubit  , with fidelity FGHZ = 〈GHZ|ρGHZ|GHZ〉 = 0.59±0.01 (
, with fidelity FGHZ = 〈GHZ|ρGHZ|GHZ〉 = 0.59±0.01 ( not shown), is formed between Q2, Q3 and Q4, as shown in Fig. 3e. This state is found to satisfy the entanglement witness inequality FGHZ>1/2 (ref. 32), indicating three-qubit entanglement.
not shown), is formed between Q2, Q3 and Q4, as shown in Fig. 3e. This state is found to satisfy the entanglement witness inequality FGHZ>1/2 (ref. 32), indicating three-qubit entanglement.
The third step in the runtime analysis captures all three qubits at the end of the algorithm, where the final H gate on Q2 rotates the three-qubit |GHZ〉 into |ψ3〉 = H2|GHZ〉 = (|g g g〉+|e g g〉+|g e e〉−|e e e〉)/2. Figure 3f is the real part of the density matrix with fidelity F = 〈ψ3|ρ3|ψ3〉 = 0.54±0.01. From the three-qubit QST we can trace out the register qubit to compare with the experiment where we measure only the single-qubit register and the raw probabilities of the algorithm output. Ideally, the algorithm returns the binary output 00 or 10 (including the redundant qubit) with equal probability, where the former represents a failure and the latter indicates the successful determination of r = 2. We use three methods to analyse the output of the algorithm: three-qubit QST, single-qubit QST and the raw probabilities of the output register state. Figure 3g,h is the real part of the density matrices for the single-qubit output register from three-qubit QST and one-qubit QST with fidelity  for both density matrices. From the raw probabilities calculated from 150,000 repetitions of the algorithm, we measure the output 10 with probability 0.483±0.003, yielding r = 2, and after classical processing we compute the prime factors 3 and 5.
for both density matrices. From the raw probabilities calculated from 150,000 repetitions of the algorithm, we measure the output 10 with probability 0.483±0.003, yielding r = 2, and after classical processing we compute the prime factors 3 and 5.
The linear entropy Sl = 4[1−Tr(ρ2)]/3 is another metric for comparing the observed output to the ideal mixed state, where Sl = 1 for a completely mixed state33. We find Sl = 0.78 for both the reduced density matrix from the third step of the runtime analysis (three-qubit QST), and from direct single-qubit QST of the register qubit.
As an extra calibration to verify that the system possesses coherence throughout the duration of the algorithm, we remove the entangling operations and use QST to measure the single-qubit output register. The circuit reduces to two H gates separated by the time of the two entangling gates, equivalent to the time of the full algorithm. Ideally Q2 returns to the ground state and the algorithm output is 0 100% of the time. Figure 3i is the real part of the density matrix for the register qubit after running this calibration. The fidelity of measuring the register qubit in |g〉 is Fcal = 〈g|ρcal|g〉 = 0.83±0.01, indicating that the system is coherent over the algorithm time.
We have implemented a compiled version of Shor’s algorithm on a quantum processor that correctly finds the prime factors of 15. We showed that the quantum processor can create Bell states, both classes of three-qubit entanglement and the requisite entanglement for properly executing Shor’s algorithm. In addition, we produce coherent interactions between four qubits and the bus resonator with a protocol that can be scaled to create an N-qubit |W〉 state, by adding more qubits to the bus resonator. During these coherent interactions, we observe the  dependence of the effective coupling strength with the number N of participating qubits. These demonstrations represent an important milestone for superconducting qubits, further proving this architecture for quantum computation and quantum simulations.
dependence of the effective coupling strength with the number N of participating qubits. These demonstrations represent an important milestone for superconducting qubits, further proving this architecture for quantum computation and quantum simulations.
References
Shor, P. Proc. 35th Annual Symp. Foundations of Computer Science 124–134 (IEEE, 1994).
Vandersypen, L. M. et al. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001).
Lanyon, B. et al. Experimental Demonstration of a compiled version of Shors algorithm with quantum entanglement. Phys. Rev. Lett. 99, 250505 (2007).
Lu, C-Y., Browne, D., Yang, T. & Pan, J-W. Demonstration of a compiled version of shors quantum factoring algorithm using photonic qubits. Phys. Rev. Lett. 99, 250504 (2007).
Politi, A., Matthews, J. C. F. & O’Brien, J. L. Shor’s quantum factoring algorithm on a photonic chip. Science 325, 1221 (2009).
Bigourd, D., Chatel, B., Schleich, W. & Girard, B. Factorization of numbers with the temporal Talbot effect: Optical implementation by a sequence of shaped ultrashort pulses. Phys. Rev. Lett. 100, 030202 (2008).
Gilowski, M. et al. Gauss sum factorization with cold atoms. Phys. Rev. Lett. 100, 030201 (2008).
Ng, H. & Nori, F. Quantum phase measurement and Gauss sum factorization of large integers in a superconducting circuit. Phys. Rev. A 82, 042317 (2010).
Clarke, J. & Wilhelm, F. K. Superconducting quantum bits. Nature 453, 1031–1042 (2008).
Hofheinz, M. et al. Generation of Fock states in a superconducting quantum circuit. Nature 454, 310–314 (2008).
Ansmann, M. et al. Violation of Bell’s inequality in Josephson phase qubits. Nature 461, 504–506 (2009).
Neeley, M. et al. Generation of three-qubit entangled states using superconducting phase qubits. Nature 467, 570–573 (2010).
Dicarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010).
Altomare, F. et al. Tripartite interactions between two phase qubits and a resonant cavity. Nature Phys. 6, 777–781 (2010).
Yamamoto, T. et al. Quantum process tomography of two-qubit controlled-Z and controlled-NOT gates using superconducting phase qubits. Phys. Rev. B 82, 184515 (2010).
Mariantoni, M. et al. Implementing the quantum von Neumann architecture with superconducting circuits. Science 334, 61–65 (2011).
Fink, J. et al. Dressed collective qubit states and the Tavis–Cummings Model in Circuit QED. Phys. Rev. Lett. 103, 083601 (2009).
Steffen, M. et al. State tomography of capacitively shunted phase qubits with high fidelity. Phys. Rev. Lett. 97, 050502 (2006).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Barenco, A. et al. Elementary gates for quantum computation. Phys. Rev. A 52, 3457–3467 (1995).
Lucero, E. et al. High-fidelity gates in a single Josephson qubit. Phys. Rev. Lett. 100, 247001 (2008).
Lucero, E. et al. Reduced phase error through optimized control of a superconducting qubit. Phys. Rev. A 82, 042339 (2010).
DiCarlo, L. et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240–244 (2009).
Tessier, T., Deutsch, I., Delgado, a. & Fuentes-Guridi, I. Entanglement sharing in the two-atom Tavis-Cummings model. Phys. Rev. A 68, 062316 (2003).
Beckman, D., Chari, A., Devabhaktuni, S. & Preskill, J. Efficient networks for quantum factoring. Phys. Rev. A 54, 1034–1063 (1996).
Buscemi, F. Shors quantum algorithm using electrons in semiconductor nanostructures. Phys. Rev. A 83, 012302 (2011).
Hofheinz, M. et al. Synthesizing arbitrary quantum states in a superconducting resonator. Nature 459, 546–549 (2009).
Lucero, E. Computing prime factors on a Josephson phase-qubit architecture: 15 = 3×5. PhD thesis, Univ. California (2012).
Jaynes, E. & Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89–109 (1963).
Mlynek, J. A. et al. Time resolved collective entanglement dynamics in cavity quantum electrodynamics. Preprint at http://arxiv.org/abs/1202.5191 (2012).
Hill, S. & Wootters, W. Entanglement of a pair of quantum bits. Phys. Rev. Lett. 78, 5022–5025 (1997).
Acı´n, a., Bruß, D., Lewenstein, M. & Sanpera, a. Classification of mixed three-qubit states. Phys. Rev. Lett. 87, 040401 (2001).
White, A. G. et al. Measuring two-qubit gates. J. Opt. Soc. Amer. B 24, 172–183 (2007).
Acknowledgements
Devices were made at the UCSB Nanofabrication Facility, a part of the NSF-funded National Nanotechnology Infrastructure Network. This work was supported by IARPA under ARO awards W911NF-08-1-0336 and W911NF-09-1-0375. R.B. acknowledges support from the Rubicon program of the Netherlands Organisation for Scientific Research. M.M. acknowledges support from an Elings Postdoctoral Fellowship. The authors thank S. Ashhab and A. Galiautdinov for useful comments on rapid entanglement.
Author information
Authors and Affiliations
Contributions
E.L. fabricated the sample, performed the experiments and analysed the data. E.L. and J.M.M. designed the custom electronics. E.L., M.M. and D.S. contributed to software infrastructure. All authors contributed to the fabrication process, qubit design, experimental set-up and manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Lucero, E., Barends, R., Chen, Y. et al. Computing prime factors with a Josephson phase qubit quantum processor. Nature Phys 8, 719–723 (2012). https://doi.org/10.1038/nphys2385
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2385
This article is cited by
-
Effective prime factorization via quantum annealing by modular locally-structured embedding
Scientific Reports (2024)
-
Concrete quantum cryptanalysis of binary elliptic curves via addition chain
Quantum Information Processing (2024)
-
Computing Shor’s algorithmic steps with interference patterns of classical light
Scientific Reports (2022)
-
Quantum modular multiplier via binary-exponent-based recombination
Quantum Information Processing (2022)
-
Using Shor’s algorithm on near term Quantum computers: a reduced version
Quantum Machine Intelligence (2022)