Extensive characterization and implementation of a family of three-qubit gates at the coherence limit

Abstract

While all quantum algorithms can be expressed in terms of single-qubit and two-qubit gates, more expressive gate sets can help reduce the algorithmic depth. This is important in the presence of gate errors, especially those due to decoherence. Using superconducting qubits, we have implemented a three-qubit gate by simultaneously applying two-qubit operations, thereby realizing a three-body interaction. This method straightforwardly extends to other quantum hardware architectures, requires only a firmware upgrade to implement, and is faster than its constituent two-qubit gates. The three-qubit gate represents an entire family of operations, creating flexibility in the quantum-circuit compilation. We demonstrate a process fidelity of 97.90%, which is near the coherence limit of our device. We then generate two classes of entangled states, the Greenberger–Horne–Zeilinger and Dicke states, by applying the new gate only once; in comparison, decompositions into the standard gate set would have a two-qubit gate depth of two and three, respectively. Finally, we combine characterization methods and analyze the experimental and statistical errors in the fidelity of the gates and of the target states.

Introduction

Quantum algorithms are generally developed using single-qubit and two-qubit gates as the basis of the instruction set^1,2. All quantum algorithms can be decomposed into a minimal universal gate set consisting of such elements; however, this is not a requirement. Taking advantage of hardware-aware compilation or using larger-than-minimal gate sets can help reduce the algorithmic depth^3,4: shallow quantum circuits are paramount in the presence of decoherence. Moreover, parameterized families of two-qubit interactions have enhanced the capabilities of quantum hardware by reducing the circuit depth⁴, improving the success probability of algorithms⁵, or allowing more expressive gates tailored to specific problems^6,7.

Three-qubit gates, such as the Toffoli and Fredkin gates, are central components of several quantum algorithms^8,9,10,11. However, when only standard single- and two-qubit gate sets are available, compiling these three-qubit gates results in considerable overheads of additional gates^1,12,13. There have been several implementations of three-qubit gates using hardware-aware compilation in order to minimize the number of applied control pulses^{14,15,16,17,18,19}, but these increase the depth of circuits and complicate calibration procedures. Having access to a native three-qubit gate implemented with a single control at the hardware level would therefore be beneficial. Unfortunately, the types of three-body interactions that naturally produce these gates can be difficult to engineer.

Single-control, multi-qubit gates have been implemented in trapped-ion systems²⁰, spin-qubit systems²¹, and superconducting qubits²². However, many of these implementations suffer from drawbacks that limit the control, fidelity of operation, and extension to larger circuits. For example, Levine et al.²⁰ relied on numerical optimization of the pulse, increasing the complexity of recalibration in the presence of drift. Roy et al.²² engineered an effective three-qubit system from the collective modes of a Josephson ring modulator and implemented a gate set comprised of only three-qubit conditional operations; however, lacking native single- and two-qubit gates, these must be compiled, increasing the circuit depth.

Recent work has modeled^23,24,25,26 or experimentally demonstrated²⁷ methods of implementing three-qubit gates through the simultaneous application of two-qubit gates. In particular, Gu et al.²³ analyzed a general model of three-body interactions generated by simultaneously driving two-qubit interactions through an intermediate state. Such an implementation can be seen as a ‘firmware’ upgrade—meaning no changes to the underlying hardware, only to the control—and the physical gate set can be readily extended to include native three-qubit gates.

In this work, we demonstrate the three-qubit Controlled-CPHASE-SWAP gate (CCZS) in a single application of the pulse controls, as proposed in ref. ²³. The resulting three-qubit interaction is faster than the individual constituent operations and implements a three-qubit gate that shares similarities with Fredkin-like gates. For specific parameters, it has the structure of a controlled-fermionic SWAP gate, which we call a fermionic Fredkin (fFredkin) gate. Furthermore, with the addition of a CZ gate, the CCZS gate can be compiled into an iFredkin gate. We use the CCZS gate to demonstrate that we can implement an entire family of three-qubit operations characterized by the SWAP phase, which could aid in variational-type algorithms. We additionally demonstrate the rapid generation of entangled GHZ²⁸ and W²⁹ states in a single application of this three-qubit operation.

The characterization of quantum processes and quantum states is non-trivial. Techniques that map all errors to stochastic errors can be efficient in the required resources^30,31 but come at the expense of losing the ability to identify the specific source of these errors, and at worst, the reported values can be disconnected from the average gate fidelity^32,33,34 they are meant to indicate. Particularly, careful treatment is needed not to wash out coherent errors, which hint at cross-talk or miscalibration, via this mapping to stochastic errors.

The most detailed methods for characterization are those of the tomography family (not necessarily limited to state, process, and gate set tomography). Gate set tomography (GST)³⁵ provides the most detailed information but rapidly becomes intractable for many qubits. By separately characterizing the state preparation and measurement (SPAM) errors associated with single-qubit operations, we demonstrate that we can use single-qubit GST to mitigate the errors intrinsic to multi-qubit quantum process tomography. This detailed analysis allows us to distinguish between control errors and decoherence and demonstrate that we are near the coherence-limited performance of our device for the CCZS gate.

Results

Device description

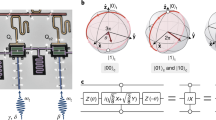
Our experiment is conducted on three qubits (Q₀, Q₁, Q₂) of a five-qubit superconducting quantum processor, as shown in Fig. 1a, and states are ordered as such in ket notation. The qubits are fixed-frequency transmon qubits³⁶, each with individual control lines and readout resonators. Qubit–qubit interactions are mediated using flux-tunable transmon qubits (C₁, C₂), referred to as couplers. The couplers are not considered in the computational space. This architecture with tunable couplers is flexible in that it allows for several types of two-qubit gates to be performed^37,38,39. The Hamiltonian of the circuit depicted in Fig. 1b is modeled as

$$\begin{array}{ll}\frac{H}{\hslash }\,=\,\mathop{\sum }\limits_{i=0}^{2}{\omega }_{i}{a}_{i}^{{\dagger} }{a}_{i}+\frac{{\eta }_{i}}{2}{a}_{i}^{{\dagger} }{a}_{i}({a}_{i}^{{\dagger} }{a}_{i}-1)\\ \qquad+\mathop{\sum }\limits_{j=1}^{2}{\omega }_{{c}_{j}}({{{\Phi }}}_{j}){b}_{j}^{{\dagger} }{b}_{j}+\frac{{\eta }_{{c}_{j}}}{2}{b}_{j}^{{\dagger} }{b}_{j}({b}_{j}^{{\dagger} }{b}_{j}-1)\\ \qquad+\mathop{\sum}\limits_{i,j}{J}_{ij}({a}_{i}^{{\dagger} }+{a}_{i})({b}_{j}^{{\dagger} }+{b}_{j}).\end{array}$$

(1)

The frequencies of the fixed-frequency qubits i (couplers j) are given by ω_i (${\omega }_{{c}_{j}}$ parameterized by magnetic flux ${\Phi_{j}}$). Each element of the system is modeled as a multi-level transmon with anharmonicity η_i and annihilation (creation) operators a_i (${a}_{i}^{{\dagger} }$), b_j (${b}_{j}^{{\dagger} }$). Couplings between fixed-frequency qubits and couplers are denoted J_ij. The couplers can be eliminated from the dynamics of the Hamiltonian via a Schrieffer–Wolff transformation when they are in the dispersive regime ($| \frac{{J}_{ij}}{{\omega }_{i}-{\omega }_{{c}_{j}}({{{\Phi }}}_{j})}| \ll 1$)^{26,38,39,40,41,42}.

Fig. 1: Schematic of superconducting quantum processor and three-qubit gate operation.

a Optical micrograph of the quantum processor. The three shown qubits (Q₀,Q₁,Q₂) are used in this work. The couplers (C₁,C₂) mediate coupling between neighboring qubits. b Reduced circuit diagram of the three-qubit device. c Energy levels of the Λ- and V-systems. AC pulses are applied at the CZ transition frequencies (${\omega }_{{{{{\rm{Q}}}}}_{0}{{{{\rm{Q}}}}}_{1}}^{{{{\rm{CZ}}}}}$, ${\omega }_{{{{{\rm{Q}}}}}_{0}{{{{\rm{Q}}}}}_{2}}^{{{{\rm{CZ}}}}}$) corresponding to driving Q₀ to the $\left\vert 2\right\rangle$ state. Individual drives activate two-qubit CZ gates, whereas simultaneous drives activate an effective three-body interaction in the Λ- and V-systems. The drives may be detuned from the true transition frequency due to miscalibration or Stark shifting during the drive, which must be corrected. d Population transfer in the Λ-system after initializing $\left\vert 110\right\rangle$. The Λ-system in (c) (bottom level structure) defines the SWAP component, whereas a round trip in the V-system (top level structure) causes the CCPHASE component (not shown).

The resulting interactions between pairs of qubits are generated by modulating the frequency of their shared tunable coupler. This is achieved by sending an AC signal to the SQUID of the coupler via a flux-bias line (Z₁ and Z₂ in Fig. 1a) of the form ${{{\Phi }}}_{j}(t)={{{\Phi }}}_{{b}_{j}}+{{{\Omega }}}_{j}(t)\cos ({\omega }_{{d}_{j}}t+{\phi }_{j})$, where ${{{\Phi }}}_{{b}_{j}}$ is the DC bias and Ω_j(t) is the pulse envelope. We use a cosine rise and fall of 25 ns with flat time τ. ${\omega }_{{d}_{j}}$ and ϕ_j are the AC driving frequency and phase of the signal, respectively. By modulating the coupler at the frequency difference between eigenstates of the qubits, as depicted in Fig. 1c, we selectively turn on interactions between pairs of qubits. In our case, we couple the $\left\vert 200\right\rangle$ state of the system to the $\left\vert 110\right\rangle$ or $\left\vert 101\right\rangle$ states when we are in the two-excitation manifold, or we couple $\left\vert 111\right\rangle$ to $\left\vert 201\right\rangle$ or $\left\vert 210\right\rangle$ in the three-excitation manifold. These transitions correspond to driving at a transition frequency given by ${\omega }_{{{{{\rm{Q}}}}}_{0}{{{{\rm{Q}}}}}_{i}}^{{{{\rm{CZ}}}}}=| {\omega }_{{{{{\rm{Q}}}}}_{i}}-{\omega }_{{{{{\rm{Q}}}}}_{0}}-{\eta }_{{{{{\rm{Q}}}}}_{0}}|$. This interaction generates a time-dependent coupling J_0i(${\Phi_{j}}$)^{26,38,39,40,41,42}. We define the effective quasistatic gate strength to be the time that implements a CZ gate, ${t}_{g}^{CZ}=\pi /| {\tilde{J}}_{0i}|$, corresponding to a round trip from one of the initial computational states to $\left\vert 200\right\rangle$ and back.

Simultaneous driving dynamics

Several proposals have been made for implementing effective three-qubit interactions^23,24,25,27. In superconducting qubits, one such proposal has recently been demonstrated by applying simultaneous cross-resonance gates²⁷. We follow an alternative schema based on the simultaneous parametric driving of tunable couplers as laid out in Gu et al.²³ based on driving non-adiabatic holonomic gates^43,44. These results are general and can be readily applied to any doubly driven three-qubit system that has a similar level structure.

The simultaneous drives activate a Λ-system, spanned by the states $\{\left\vert 110\right\rangle ,\left\vert 200\right\rangle ,\left\vert 101\right\rangle \}$ within the two-excitation manifold, and a V-system, spanned by $\{\left\vert 201\right\rangle ,\left\vert 111\right\rangle ,\left\vert 210\right\rangle \}$ in the three-excitation manifold (Fig. 1c). For these two systems, the dynamics are described by the same Hamiltonian in the interaction picture

$$H=\left[\begin{array}{ccc}-{\delta }_{1}&{\tilde{J}}_{01}&0\\ {\tilde{J}}_{01}^{* }&0&{\tilde{J}}_{02}\\ 0&{\tilde{J}}_{02}^{* }&-{\delta }_{2}\end{array}\right].$$

(2)

The terms δ_i represent the detuning of the respective drives from the CPHASE transition frequency. The simultaneous drives activate a CSWAP between Q₁ and Q₂ and additionally cause a CCPHASE when Q₀ is in $\left\vert 1\right\rangle$, in a time

$${t}_{g}^{CCZS}=\frac{\pi }{\sqrt{| {\tilde{J}}_{01}{| }^{2}+| {\tilde{J}}_{02}{| }^{2}+{(\delta /2)}^{2}}}.$$

(3)

The resulting three-qubit gate under the evolution of (2) after a time ${t}_{g}^{CCZS}$ has the form²³ (see Supplementary Note 4)

$${U}_{{{{\rm{CCZS}}}}}(\theta ,\phi ,\gamma )=\left\vert 0\right\rangle {\left\langle 0\right\vert }_{0}\otimes {I}_{1}\otimes {I}_{2}+\left\vert 1\right\rangle {\left\langle 1\right\vert }_{0}\otimes {U}_{{{{\rm{CZS}}}}}(\theta ,\phi ,\gamma )$$

(4)

with

$$\begin{array}{lll}&&{U}_{{{{\rm{CZS}}}}}(\theta ,\phi ,\gamma )=\\ &&\left[\begin{array}{cccc}1&0&0&0\\ 0&-{e}^{i\gamma }{\sin }^{2}\frac{\theta }{2}+{\cos }^{2}\frac{\theta }{2}&{e}^{i(\frac{\gamma }{2}-\phi )}\cos \frac{\gamma }{2}\sin \theta &0\\ 0&{e}^{i(\frac{\gamma }{2}+\phi )}\cos \frac{\gamma }{2}\sin \theta &-{e}^{i\gamma }{\cos }^{2}\frac{\theta }{2}+{\sin }^{2}\frac{\theta }{2}&0\\ 0&0&0&-{e}^{-i\gamma }\end{array}\right].\end{array}$$

(5)

The three-qubit gate has three parameters: the SWAP angle θ; the SWAP phase ϕ; and the CCPHASE phase γ, resulting in an entire family of three-qubit interactions. Experimentally, these angles are given by

$$\tan \frac{\theta }{2}{e}^{i\phi }=\,\frac{\tilde{{J}}_{01}}{\tilde{{J}}_{02}},$$

(6)

$$\gamma =\,\frac{\pi \delta }{\sqrt{4(| {\tilde{J}}_{01}{| }^{2}+| {\tilde{J}}_{02}{| }^{2})+{\delta }^{2}}}.$$

(7)

The SWAP phase ϕ is controlled by the relative phase between the two AC flux drives, ϕ = ϕ₁ − ϕ₂. Virtual Z rotations are additionally applied to update the local frame of the qubits^5,45 after the application of the gate.

Of particular interest are the dynamics when the constituent two-qubit gates are of the same strength, i.e., $| {\tilde{J}}_{01}| =| {\tilde{J}}_{02}|$, and when the drives are in resonance with their corresponding transitions, δ = 0. With these parameters, we obtain the gate

$${U}_{{{{\rm{CZS}}}}}(\pi /2,\phi ,0)=\left[\begin{array}{cccc}1&0&0&0\\ 0&0&{e}^{-i\phi }&0\\ 0&{e}^{i\phi }&0&0\\ 0&0&0&-1\end{array}\right],$$

(8)

which is implemented in a time ${t}_{g}^{{{{\rm{CZ}}}}}/{t}_{g}^{{{{\rm{CCZS}}}}}=\sqrt{2}$ times faster than the constituent two-qubit gates (3). For the instance of ϕ = 0, we obtain a controlled-fermionic SWAP or fFredkin gate⁴⁶.

Determination of gate parameters

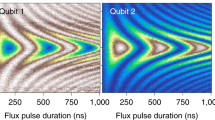
We begin validating the driven model by first individually tuning up two pulses with equal effective coupling strengths ${\tilde{J}}_{0i}/2\pi=2.833\,{{{\rm{MHz}}}}$ ($\sim$ 353 ns pulse length) yielding θ = π/2. We then apply the pulse sequence as depicted in the inset of Fig. 1d, preparing the state $\left\vert 110\right\rangle$.

In order to achieve the resonance condition, δ = 0, we perform two measurements in which we sweep the plateau of the simultaneous pulses as well as the frequency of one of the couplers’ drives while keeping the other fixed. This produces oscillations in the Λ-system, which are fit to extract the frequency detunings δ₁ and δ₂ (see Supplementary Note 3) as well as ensure equal coupling strengths. The population transfers of Fig. 1d correspond to a linecut in this 3D dataset (see Supplementary Fig. 2) where δ₁ = δ₂ = 0, with a corresponding fit to the dynamics modeled in (2).

The resonance condition (and thus γ = 0) is verified by performing the two experiments shown in the inset of Fig. 2a. In the first, we prepare the state $\left\vert 1+0\right\rangle$ and apply the U_CCZS(π/2, ϕ₀, γ) gate to swap the state for some, at the moment unknown, SWAP phase ϕ₀. We then sweep the angle of a Z rotation on Q₂ and measure on either the X or Y basis. In the second experiment, we apply a NOT gate on the third qubit to prepare $\left\vert 1+1\right\rangle$. The relative phase of the resulting superpositions is only sensitive to variations in γ. For any ϕ, the two preparations oscillate π out of phase when the resonance condition is achieved (δ₁ = δ₂ = 0).

Fig. 2: Calibration and characterization of three-qubit gate CCPhase and CSWAP phase.

a Calibration and verification of γ (or equivalently δ) similar to typical CZ calibration³⁹. We use $\left\vert 1+0\right\rangle$ and $\left\vert 1+1\right\rangle$ as probe states, as they are insensitive to the currently unknown SWAP phase, ϕ₀, and oscillate γ + π out of phase of one another. b Performing a cross-Ramsey experiment using Q₁ prepared in $\left\vert +\right\rangle$ and using the three-qubit gate to SWAP the population to Q₂. We define ϕ = 0 from the phase that maximizes the expectation value in I ⊗ I ⊗ X. We additionally demonstrate full SWAP-phase control regardless of input state after calibration of γ = 0.

To determine the unknown SWAP phase ϕ₀, we run the circuit in the inset of Fig. 2b. We prepare the input state $\left\vert 1+0\right\rangle$ and then apply the simultaneous pulses while sweeping the phase of one of the AC drives relative to the other. The gate swaps the superposition state on Q₁ to Q₂, accumulating a phase at the difference between the individual phases of the two drives. We reference ϕ = 0 to the phase difference between drives which maximizes the expectation value 〈IIX〉 for the $\left\vert 1+0\right\rangle$ state. Additionally, we demonstrate full control over ϕ by repeating the measurement with all eigenstates of X, $\left\vert \pm \right\rangle =\frac{1}{\sqrt{2}}(\left\vert 0\right\rangle \pm \left\vert 1\right\rangle )$, and Y, $\left\vert {i}^{\pm }\right\rangle =\frac{1}{\sqrt{2}}(\left\vert 0\right\rangle \pm i\left\vert 1\right\rangle )$, initialized on Q₁. We find coherent oscillations regardless of input state, demonstrating that we implement an entire family of three-qubit gates with the SWAP phase being a free parameter.

Gate characterization

With the CCZS gate tuned up, we move on to characterization. We aim to obtain a measure of the fidelity of the gate independent of state preparation and measurement (SPAM) errors. Several methods exist for this^7,47,48, but we seek more explicit information to trace whether the errors are the result of miscalibration, decoherence, or parasitic terms in the Hamiltonian. To achieve this, we use standard quantum process tomography (QPT)⁴⁹.

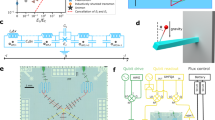
Process tomography is generally referenced to idealized state preparations, rotation operators, and detectors, making it difficult to separate SPAM errors from the process being characterized^35,50. To remedy this, we modify the protocol by separately performing gate set tomography (GST)³⁵ on the single-qubit operations to obtain a model of the noisy initial states, noisy single-qubit rotations, and the single-qubit positive-operator valued measures (POVM) corresponding to readout. With these priors, we condition the QPT reconstruction to characterize our SPAM-free process⁵¹. The exact procedure is depicted in Fig. 3a and outlined in “Methods”.

Fig. 3: Reconstruction procedure and results of three-qubit CCZS gate.

a Reconstruction procedure for QPT. Standard QPT is first performed to collect the 64 × 27 datasets comprising the reconstruction. Separately, single-qubit GST is performed to extract the noisy groundstates, rotation gates, and POVMs for the three qubits, which are used in the reconstruction to separate SPAM errors. b The ideal unitary of ${U}_{CCZS}(\frac{\pi }{2},\frac{\pi }{2},0)$ and the leading Kraus (LK) matrix obtained from the Kraus operators. The LK matrix captures the majority of the dynamics of a noisy channel⁶². c Bootstrap distributions for a chosen SWAP angle of $\phi =\frac{\pi }{2}$ over N_boot = 1000. The “raw” process fidelity compares against the target unitary, whereas the control-error-free fidelity mitigates for imperfections in the U_CCZS(θ, ϕ, γ) calibration. d Coherence limit of the three-qubit gate given the T₁, T₂ values with 95% confidence interval (see Supplementary Note 5), the raw fidelity of the reconstruction, and the control-error-free fidelity with 2σ error.

For the reconstruction, we use the projected least-squares (PLS) method^52,53 to obtain the Choi matrix⁵⁴, ρ_Φ, of the noisy quantum process, Φ. The PLS method finds a least-squares estimate of the Choi matrix and then iteratively projects it into the space of completely positive trace-preserving (CPTP) maps which preserve the physicality of the process. The procedure also provides guarantees of error bounds, which more familiar methods, such as maximum likelihood estimation (MLE), do not. We opt to use a least-squares estimate rather than the more familiar MLE due to the simplicity of implementation, statistical guarantees of the protocol, and lack of several pathological limitations associated with MLE, which have been well studied^50,55,56,57.

In the Choi representation, a quantum channel evolves an input state ρ as

$${\rho }^{{\prime} }={{\Phi }}(\rho )={{{{\rm{Tr}}}}}_{a}(({\rho }^{T}\otimes {I}_{d}){\rho }_{{{\Phi }}}),$$

(9)

where I_d is the identity operator on a Hilbert space of dimension, d, equal to our system, and we take the partial trace over the input state’s system.

From the reconstructed Choi matrix ρ_Φ, we can transform to any other representation of a quantum process, such as to compute the process fidelity with the Chi matrix^58,59,60

$$F(\chi ,\tilde{\chi })={{{\rm{Tr}}}}\left({\sqrt{\sqrt{\tilde{\chi }}\chi \sqrt{\tilde{\chi }}}}\right)^{2}.$$

(10)

χ and $\tilde{\chi }$ are Chi matrices representing two quantum processes. This definition of fidelity is convenient to work with, as it generalizes the notion of fidelity between both superoperators and density matrices, where χ could be replaced by any density matrix ρ. Also, by mapping a quantum process to the Kraus representation, we can identify the dominant evolution^61,62 to obtain a quantum truth table, as shown in Fig. 3b. This provides a connection to phase information as well as the classical mapping of input states.

However, the reconstruction only obtains a point estimate of the quantum process and the fidelity given our observations. Ideally, we would like to construct confidence intervals over the fidelity and over the space of possible reconstructions. We bootstrap the reconstruction by repeatedly sampling from the observed empirical distributions. Each newly sampled dataset represents possible experimental outcomes given the sample error of each QPT measurement^63,64. We report the average fidelity over the resulting distribution and the uncertainty rather than the point estimate. The process fidelity of the three-qubit gate for all angles of ϕ is summarized in Table 1 for the 250 ns three-qubit gate time that results from constituent 353 ns two-qubit operations. We find that the process fidelity is near the coherence limit of 98.30% (Supplementary Note 3), as seen in Fig. 3d, and well within a 95% confidence interval of the fluctuations of the coherence of our device.

Table 1 Reconstructed fidelities and extracted parameters for a family of three-qubit CCZS gates.

There is an identifiable dependence of the fidelity on the SWAP phase ϕ, as seen in Fig. 3d, where the fidelity drops slightly until ϕ = π/2 then increases again. While the decrease in fidelity lies within the typical fluctuations of the device, if we assume this trend is real, we can attempt to isolate the cause during the bootstrapping loop. We first perform the reconstruction and then optimize over the angles of an ideal CCZS gate to find the parameters $(\tilde{\theta },\tilde{\phi },\tilde{\gamma })$ that maximize the fidelity with respect to the reconstructed process (see Fig. 3c, d). We term this fidelity the control-error-free fidelity, ${{{{\mathcal{F}}}}}_{\text{CEF}}$, and the fidelity from the reconstruction to the ideal target parameters as the “raw” fidelity, ${{{{\mathcal{F}}}}}_{{{{\rm{raw}}}}}$. If the ϕ-dependence were purely due to drift in the controls or miscalibration, this optimization procedure should lift the dependency and flatten the fidelity along the coherence limit.

While there are miscalibrations between the ideal target parameters (Table 1), the seeming dependence on ϕ remains. Leakage to the couplers or population outside the computational space is excluded, as leakage would be phase-independent. The sensitivity of exchange-like interactions to residual ZZ parasitic terms has been well documented in superconducting qubits^{37,39,65,66,67} and could explain the resulting phase dependence. However, without further analysis, it would be difficult to separate the influence of these parasitic terms from a fluctuation in coherence; such studies will be the subject of follow-up work.

Rapid generation of entangled states

As a demonstration of the gate, we opt to use the CCZS gate in two different modes of operation. In the first, Fig. 4a, b, we treat the three-qubit gate as acting solely within the computational subspace and prepare a GHZ state, $(\left\vert 000\right\rangle +\left\vert 111\right\rangle )/\sqrt{2}$, in a single application of the CCZS. With only two-qubit operations, this requires the application of two sequential two-qubit gates. We achieve a state fidelity of 95.56 (16)% [using (10)] after mitigating measurement errors.

Fig. 4: Quantum state tomography of GHZ and W states using CCZS gate.

a, c Density matrix of the GHZ and W states with their magnitudes and phases plotted for each basis element. The theoretical values are plotted as the wireframes around the solid bars. b, d Expectation values of the different experimentally obtained Pauli observables and the ideal theoretical expectations and the corresponding circuits (insets) for generating the respective states.

In the second case, Fig. 4c, d, we allow for evolution outside of the computational subspace and apply the CCZS gate for approximately half the time (denoted a $\sqrt{{{{\rm{CCZS}}}}}$ gate) using the same gate parameters. This alternative implementation leverages the qutrit space to rapidly generate the W state.

Hence, in our circuit (see inset of Fig. 4d), we first prepare the state $\sqrt{1/3}\left\vert 000\right\rangle +\sqrt{2/3}\left\vert 100\right\rangle$ by applying a rotation ${R}_{y}(2\arccos \sqrt{1/3})$ to Q₀. We then apply a calibrated X_1→2 pulse to perform a NOT operation in the qutrit space and map the population in $\left\vert 100\right\rangle$ to $\left\vert 200\right\rangle$. From here, the application of the $\sqrt{CCZS}$ gate divides the population in $\left\vert 200\right\rangle$ to states $\left\vert 101\right\rangle$ and $\left\vert 110\right\rangle$, resulting in the state $(\left\vert 000\right\rangle +{e}^{i{\phi }_{1}}\left\vert 110\right\rangle +{e}^{i{\phi }_{2}}\left\vert 101\right\rangle )/\sqrt{3}$. A final NOT gate applied to Q₀ completes the generation of the W state up to locally correctable phases with single-qubit R_z gates. This three-qutrit gate is implemented in 133 ns and generates the W state with a fidelity of 94.71(21)%.

The rapid generation of larger Dicke states across a lattice could also be achieved by simultaneously driving iSWAP operations between all pairs of qubits without having to make an excursion outside of the computational subspace²³ by collectively coupling qubits to a common mode⁶⁸ or bringing all qubits into resonance^69,70. However, in the context of the CCZS gate and logical operations, in an architecture with limited connectivity, we find that our three-qubit gate always outperforms the compilation using two-qubit gates without the need for tailored architectures.

We find that generating the GHZ and W states using the native three-qubit gate always outperforms the equivalent circuit decomposed into single and two-qubit gates. We show the infidelity of generating the GHZ and W states in Fig. 5a, b, respectively. Simulations are performed taking into account multi-level effects using the experimental parameters in Supplementary Table 1. All single-qubit gates take ${t}_{g}^{1{{{\rm{q}}}}}=$ 20 ns to implement in our hardware.

Fig. 5: Comparison of coherence limits of GHZ and W states via compilation to two- or three-qubit gates.

a Coherence limits of GHZ state preparation using two-qubit CZ gates and the three-qubit CCZS gate. The two-qubit decomposition is given in the inset, whereas the preparation using the CCZS gate is shown in Fig. 4b. Similarly, in b, we compare the coherence limits of generating the W state using an optimal two-qubit decomposition using the CZ gate and the qutrit version of the CCZS gate described in the main text and shown in Fig. 4d.

The CZ gates set the timescale for implementing the three-qubit gate according to (3). This gives the three-qubit gate a $\sqrt{2}$ speedup over the CZ gates. Compiling the GHZ circuits to minimize total runtime gives

$${t}_{2{{{\rm{q}}}}}^{{{{\rm{GHZ}}}}}=2{t}_{g}^{1{{{\rm{q}}}}}+2{t}_{g}^{{{{\rm{CZ}}}}},$$

(11)

$${t}_{3{{{\rm{q}}}}}^{{{{\rm{GHZ}}}}}=2{t}_{g}^{1{{{\rm{q}}}}}+\frac{{t}_{g}^{{{{\rm{CZ}}}}}}{\sqrt{2}}.$$

(12)

Using the three-qubit gate, we exploit the higher energy levels of the transmon to generate the W state. Therefore, the CCZS gate is applied for only half its gate time, resulting in a $2\sqrt{2}$ speedup over the CZ gate. The total runtime for the two circuits then scales as

$${t}_{2{{{\rm{q}}}}}^{{{{\rm{W}}}}}=4{t}_{g}^{1{{{\rm{q}}}}}+3{t}_{g}^{{{{\rm{CZ}}}}},$$

(13)

$${t}_{3{{{\rm{q}}}}}^{{{{\rm{W}}}}}=3{t}_{g}^{1{{{\rm{q}}}}}+\frac{{t}_{g}^{{{{\rm{CZ}}}}}}{2\sqrt{2}}.$$

(14)

When predominantly coherence-limited, the three-qubit gate allows for substantial shortening of the circuit depth and could significantly aid in compilation strategies.

Discussion

We demonstrated a single-step implementation of a family of three-qubit gates based on simultaneous driving of transitions to an intermediate eigenstate. These gates combine aspects of Toffoli and Fredkin gates resulting in an operation that we denote controlled-CPHASE-SWAP or CCZS. Our approach is extensible, as it can be implemented across larger qubit systems and other quantum-computing implementations. For this reason, the three-qubit gate represents a ‘firmware’ upgrade of existing systems: the only requirement is the simultaneous driving of transitions to a common eigenstate in a multi-qubit system. The calibration uses existing two-qubit gate strategies and can be straightforwardly applied to other systems. This results in process fidelities approaching the coherence limit of our device of ~98%.

Applying the CCZS gate to our hardware allowed us to rapidly prepare two different classes of entangled states. We therefore envision that this gate can be used to augment existing gate sets and leverage the multi-qubit nature to aid in the compilation of quantum algorithms. In particular, the rapid generation of GHZ states would facilitate the rapid creation and distillation of larger entangled states⁷¹, which can then be used as resources to demonstrate the power of unbounded quantum fanout gates⁷² experimentally. The CCZS gate can also be used to generate more familiar three-qubit gates, such as the iFredkin, with the addition of a single CZ gate²³, or for ϕ = 0, a fermionic Fredkin gate. Beyond the computational basis, this gate can be used to augment gate sets in qutrit systems, which has been a comparatively unexplored field.

Methods

Measurement setup

Qubit fabrication is performed as in the previous work⁷³. Additionally, we make use of aluminum crossovers to aid in routing signals across the device and for tying together ground planes of the chip. The device is packaged in a copper box and wirebonded to a palladium- and gold-plated printed circuit board (PCB). An aluminum shield with a volume is cut out around the PCB traces, and the chip is fixed atop the device to push package modes away from the operating frequencies of the device and provide an additional layer of shielding. The PCB contains 16 non-magnetic connectors, of which we use seven: two for the input and output of the readout, three for local control of the single qubits, and two for the static and AC flux control of the couplers.

The setup used in this experiment is a standard circuit-QED setup. The copper package housing the sample sits at the bottom of our Bluefors LD250 dilution refrigerator and is shielded from magnetic fields by two shields of cryoperm/mu-metal and two superconducting shields. All signal lines are attenuated and filtered to thermalize the signals coming into the fridge (see Supplementary Fig. 1).

We perform readout using a Zurich Instruments UHFQA for generating and reading out the signals. The readout pulses pass through an up/down-conversion board where the local oscillator (LO) from a Rohde & Schwarz SGS100a continuous-wave signal generator is split between both the up- and down-conversion halves. This maintains the phase coherence between the generation and digitization of the readout signals. Single-qubit pulses are synthesized using Zurich Instruments HDAWG and upconverted internally using Rohde & Schwarz SGS100a vector signal generators using internal IQ mixers. The flux drives for couplers are generated digitally by the HDAWG as the signal frequencies for our coupling gates fall within the bandwidth of the HDAWG.

Qubit frame tracking

We fix the trigger period of the measurements such that it is an even multiple of the least common multiple of the inverse of the LO frequencies of the qubits

$${\tau }_{p}=n\times {{{\rm{lcm}}}}\left(\frac{1}{{f}_{LO}^{0}},\frac{1}{{f}_{LO}^{1}},\frac{1}{{f}_{LO}^{2}}\right)$$

(15)

For the qubit LOs of 4.5 GHz, 4.5 GHz, 5 GHz, this ends up being an even multiple of 2 ns. In our case, we set our trigger period to 350 μs to allow for adequate time for the qubit to relax to the ground state and reset. This timing ensures that for every trigger, the qubits see the same phase of all drives (digital and analog). All phase control of the pulses can then be handled by digitally manipulating the carrier of the pulses generated on the HDAWG. This holds for the adjustments in the local phases of the qubits to update the qubit frame with virtual-Z gates and those of the flux drives on the couplers, allowing full control over the SWAP phase ϕ of the three-qubit gate.

Single-qubit gate set tomography

For the single-qubit gate set tomography, we first set about verifying the independence of single-qubit operations and measurements. We perform GST individually across all qubits and then perform single-qubit GST simultaneously. In doing so, we seek to find whether there is significant non-Markovianity between the two modes of operation. While we do find greater model violations between individual and simultaneous GST (see Supplementary Fig. 4), the reconstructed operations and infidelities are similar between the two runs. Non-Markovianity can also arise from drifts in parameters between the experiments as well as fluctuations in the coherence of the device, which will occur over the runtime of the GST measurements.

We perform a long-sequence GST (LSGST) set consisting of gates from the set {I, R_y(π), R_y( ± π/2), R_x( ± π/2)}. The total number of circuits performed in the analysis was 2904 separate gate sequences up to a depth of L = 16, and each circuit was sampled n = 5000 times. The circuits were generated, and results were analyzed using pyGSTi⁷⁴. From this, we extract for each qubit: the noisy initial states, ${\tilde{\rho }}_{0}$, noisy rotation operators, $\{{\tilde{R}}_{x}(\pm \pi /2),{\tilde{R}}_{y}(\pm \pi /2),{\tilde{R}}_{y}(\pi )\}$, and POVMs ${\tilde{M}}_{j}$ for mitigating the SPAM errors in the reconstruction. The results are summarized in Supplementary Tables 2 and 3. Residual initial state populations correspond to effective qubit temperatures of 50–60 mK, which are nominally the same as in state-of-the-art superconducting architectures⁷⁵.

SPAM-independent process tomography

In process tomography⁴⁹, we first prepare the input probe states ${\{\left\vert g\right\rangle ,\left\vert e\right\rangle ,\left\vert +\right\rangle ,\left\vert {i}^{+}\right\rangle \}}^{\otimes 3}$ by performing single-qubit rotations from the set ${\{I,{R}_{y}(\pi ),{R}_{y}(\pi /2),{R}_{x}(-\pi /2)\}}^{\otimes 3}$. This gives us a set of 64 input states on which we apply the process to be characterized. Finally, we rotate the outcome into the bases {X, Y, Z}^⊗3 by applying single-qubit rotations from the set ${\{{R}_{y}(-\pi /2),{R}_{x}(\pi /2),I\}}^{\otimes 3}$. This choice of rotations maintains the parity of the eigenvalue associated with each input probe state when measured in its basis so that we are left with binary output strings in the space {0, 1}^⊗3, simplifying the model of the POVMs.

Using the results of GST, we redefine the probe states in terms of the noisy initial states for the three qubits, ${\tilde{\rho }}_{0}{ = \bigotimes }_{k = 0}^{2}{\tilde{\rho }}_{0}^{k}$. We then prepare the input probe states with the noisy rotation operators, ${\tilde{{{{\bf{R}}}}}}_{i}{ = \bigotimes }_{k = 0}^{2}{\tilde{R}}^{k}$, to generate each of the 64 input states,

$${\tilde{\rho }}_{i}={\tilde{{{{\bf{R}}}}}}_{i}{\tilde{\rho }}_{0}{\tilde{{{{\bf{R}}}}}}_{i}^{{\dagger} }.$$

(16)

The process is then applied to the state using the Choi matrix according to (9). The resulting state is then rotated into its measurement basis and projected onto the set of outcomes {0, 1}^⊗3. We can represent our rotated POVM for a measurement outcome s ∈ [1, 8] and a particular Pauli basis j ∈ [1, 27] as

$${\tilde{M}}_{js}={\tilde{R}}_{j}{\tilde{M}}_{s}{\tilde{R}}_{j}^{{\dagger} }.$$

(17)

The probability that a three-qubit state has an outcome s, given a measurement basis j, and preparation i is then

$$\begin{array}{ll}{p}_{i,j,s}=Tr({\tilde{M}}_{j,s}{\tilde{\rho }}_{i}^{{\prime} })\,=\,Tr({\tilde{M}}_{j,s}\otimes {I}_{d}({\tilde{\rho }}_{i}\otimes {I}_{d}){\rho }_{{{\Phi }}})\\ \qquad\qquad\qquad\qquad\,\,\,=Tr(({\tilde{M}}_{j,s}{\tilde{\rho }}_{i}\otimes {I}_{d}){\rho }_{{{\Phi }}}).\end{array}$$

(18)

The probabilities can be written down as a vector and, since the above equation is linear, can be set up as a linear inversion problem that obtains the Choi matrix by inverting the equation

$$A\overrightarrow{{\rho }}_{{{\Phi }}}=\overrightarrow{p}.$$

(19)

Here, the matrix A contains all the information regarding the probes and measurements with $\overrightarrow{{\rho }}_{{{\Phi }}}$ and $\overrightarrow{p}$ as the flattened Choi matrix and the probabilities. The construction of A is described in ref. ⁵²; we use linear inversion of A to obtain an initial estimate of the process.

Quantum state reconstruction

For the state tomography, we prepare the states as the insets in Fig. 4b, d show and similarly measure the {X, Y, Z}^⊗3 basis. We apply the measurement mitigation we obtain from the measured POVMs and perform a least-square algorithm to reconstruct the density matrix constraining the fit to be trace-preserving. The density matrix is represented using the Cholesky decomposition, making the reconstruction manifestly positive semidefinite,

$$\rho =\frac{{T}^{{\dagger} }T}{{{{\rm{Tr}}}}{T}^{{\dagger} }T}.$$

(20)

T is a triangular matrix,

$$T=\left[\begin{array}{ccccc}{t}_{0}&0&0&\,\cdots &0\\ {t}_{{2}^{n}}+i{t}_{{2}^{n}+1}&{t}_{1}&0&\,\cdots &0\\ {t}_{3({2}^{n}-1)+1}+i{t}_{3({2}^{n}-1)+2}&{t}_{{2}^{n}+2}+i{t}_{{2}^{n}+3}&{t}_{2}&\,\cdots &0\\ \vdots &\vdots &\vdots &\ddots &0\\ \,\cdots &\,\cdots &\,\cdots &{t}_{3({2}^{n}-1)-1}+i{t}_{3({2}^{n}-1)}&{t}_{{2}^{n}-1}\end{array}\right],$$

(21)

where ${{{\bf{t}}}}=[{t}_{0},{t}_{1},\,\cdots ,{t}_{{4}^{n}-1}]$ is a set of parameters containing all real numbers t_i.

For the state tomography, we perform post-processing on the relative phases between populations of the $\left\vert {{{\rm{GHZ}}}}\right\rangle =1/\sqrt{2}(\left\vert 000\right\rangle +{e}^{i\phi }\left\vert 111\right\rangle )$ and $\left\vert {{{\rm{W}}}}\right\rangle =1/\sqrt{3}(\left\vert 100\right\rangle +{e}^{i{\phi }_{1}}\left\vert 010\right\rangle +{e}^{i{\phi }_{2}}\left\vert 001\right\rangle )$ by finding local rotations R_Z(ϕ_i) for each reconstruction which maximize the overlap with their ideal states. Neither of these local operations alters the entanglement characteristics of the resulting states.