Ramsey-type phase control of free-electron beams

Abstract

Quantum coherent evolution, interference between multiple distinct paths^1,2,3,4 and phase-controlled sequential interactions are the basis for powerful multi-dimensional optical⁵ and nuclear magnetic resonance³ spectroscopies, including Ramsey’s method of separated fields⁶. Recent developments in the quantum state preparation of free electrons⁷ suggest a transfer of such concepts to ultrafast electron imaging and spectroscopy. Here, we demonstrate the sequential coherent manipulation of free-electron superposition states in an ultrashort electron pulse, using nanostructures featuring two spatially separated near-fields with polarization anisotropy. The incident light polarization controls the relative phase of these near-fields, yielding constructive and destructive quantum interference of the subsequent interactions. Future implementations of such electron–light interferometers may provide access to optically phase-resolved electronic dynamics and dephasing mechanisms with attosecond precision.

Main

A central objective of attosecond science is the optical control over electron motion in and near atoms, molecules and solids, leading to the generation of attosecond light pulses or the study of static and dynamic properties of bound electronic wavefunctions^8,9,10,11. One of the most elementary forms of optical control is the dressing of free-electron states in a periodic field^12,13, which is observed, for example, in two-colour ionization^14,15, free–free transitions near atoms^12,16, and in photoemission from surfaces^17,18,19,20. Similarly, beams of free electrons can be manipulated by the interaction with optical near-fields^{7,21,22,23,24}. In this process, field localization at nanostructures facilitates the exchange of energy and momentum between free electrons and light. In the past few years, inelastic electron–light scattering^22,23,25 found application in so-called photon-induced near-field electron microscopy^7,21,26,27, the characterization of ultrashort electron pulses^23,24, or in work towards optically driven electron accelerators^28,29. Very recently, the quantum coherence of such interactions was demonstrated by observing multilevel Rabi-oscillations in the electron populations of the comb of photon sidebands^7,22. Access to these quantum features, gained by nanoscopic electron sources of high spatial coherence^30,31,32, opens up a wide range of possibilities in coherent manipulations, control schemes and interferometry with free-electron states.

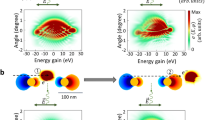
Here, we present a first implementation of quantum coherent sequential interactions with free-electron pulses. In particular, we employ a nanostructure that facilitates phase-controlled double interactions, leading to a selectable enhancement or cancellation of the quantum phase modulation in the final electron wavefunction. Figure 1a illustrates the basic principle of our approach: traversal of the first near-field induces photon sidebands (labelled 2 in Fig. 1a) to the initially narrow electron kinetic energy spectrum (labelled 1), which correspond to a sinusoidal phase modulation of the free electron wavefunction. Following free propagation, the electrons coherently interact with a second near-field and, in analogy to Ramsey’s method⁶, the final electronic state sensitively depends on the relative phase between the two acting fields. In particular, a further broadening (labelled 4) or a recompression (labelled 3) of the momentum distribution can be achieved.

Figure 1: Experimental concept and set-up.

a, Working principle of the Ramsey-type free electron interferometer: an electron pulse (green) is acted on at two spatially separated nodes g₁ and g₂. A sinusoidal phase modulation is imprinted onto the electron wavefunction during the first interaction, leading to the generation of spectral sidebands. The relative phase of the interactions governs the phase modulation of the final state. 1 to 4: experimental electron energy spectra. 1, incident spectrum. 2, Spectrum for a single interaction. 3, 4, Spectra recorded for destructive and constructive double interactions, respectively. b, Scanning electron micrographs of the nanostructure featuring two interaction zones (top and side view). Distance between gold paddles: 5 μm. c, Sketch of the experimental scenario displaying polarization-controlled excitation of the nanostructure. d, Raster-scanned image of the local coupling strength |g_tot| (see text) for excitation conditions near complete recompression in the corner region (green dashed circle, wave plate angles θ = −38°, ξ = 26°, see Fig. 3b).

For a single interaction of a free, quasi-monoenergetic electron state with an optical near-field, the resulting final state is composed of a superposition of momentum sidebands associated with energy changes by ±N photon energies^22,23, populated with amplitudes A_N according to

where J_N are the Nth-order Bessel functions. The dimensionless coupling parameter g describes the efficiency of momentum exchange with the electron and scales linearly with the longitudinal vector component of the optical near-field amplitude, that is, the electric field component parallel to the electron trajectory (denoted F_z in Fig. 1c; see also Methods ‘Sinusoidal phase modulation’). In the spatial representation of the free electron state, this Bessel-type distribution of sideband amplitudes is manifest in a sinusoidal modulation of the phase of the wavefunction in the form²³

where ψ_in and ψ_fin are the initial and final state wavefunctions, respectively, ω is the optical frequency, v is the electron velocity and z is the spatial coordinate along the electron trajectory.

In the present experiment, schematically depicted in Fig. 1a, c, we demonstrate that two spatially separated optical near-fields may cause an overall interaction of strength g_tot, which is describable as the coherent sum of the individual, generally complex-valued interactions g₁ and g₂,

where ϕ₀ is a constant phase offset that depends on the spatial separation of the interaction regions (see Methods ‘Sinusoidal phase modulation’ and ‘Coordinate system and geometric phase offset’). In terms of the spatial wavefunction, this then corresponds to an overall enhancement or cancellation of the subsequent interaction-induced phase modulations (equation (2)).

The desired control over g_tot requires the ability to separately address the two near-fields in a phase-locked manner. We achieve this by tailoring the nanostructure geometry, employing the strong polarization anisotropy of a pair of perpendicular plates (Fig. 1b). This approach allows us to control the near-field strengths and their relative phase by selecting the polarization state of the overall excitation. In the following, we describe the experimental implementation of this principle.

A narrow beam of ultrashort electron pulses passes the optically excited nanostructure in close vicinity (Fig. 1c). The final electronic state resulting from inelastic electron–light scattering is analysed by electron spectroscopy for a systematic variation of the incident light polarization. The polarization state is described by the Jones vector J, which we set in the standard fashion³³ by the combination of a half- and quarter-wave plate at rotation angles θ and ξ, respectively. The Jones vector for sample excitation is then given by the product of the initial (in our case, diagonal) polarization state and wave plate Jones matrices M, scaled by the field strength F = 0.08 V nm⁻¹: .

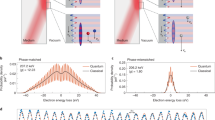
In a first set of measurements, the near-field responses of the two nanoscopic plates to the incident polarization state are independently characterized. To this end, the electron beam is placed close to each of the edges, and distant from the corner (red, blue circles in Fig. 2f), such that the electrons traverse only one of the two near-field regions in each case. Figure 2a, b displays electron spectra for a continuous variation of polarization states (achieved by wave plate rotation), including polarizations parallel and perpendicular to the plates. The widths of these spectra directly reflect the respective coupling constants g_1,2, as the highest populated sideband is given by 2 |g| (ref. 7). It is evident that both edges exhibit strong near-fields only for excitation conditions with polarization perpendicular to the respective edge orientation. This behaviour can be regarded as a linear analyser response, in which each edge projects the incident polarization state onto a quasi-polarizability α_1,2, yielding scalar coupling constants g_1,2 = α_1,2 ⋅ J. By the design of the structure, the vectors α_1,2 are linearly independent, in fact nearly orthogonal, which allows for separate amplitude and phase control.

Figure 2: Phase control of dual interaction.

a–e, Electron spectra recorded at different positions on the sample for varying incident polarization states (arrow icons). Red lines: coupling constant 2 |g_1,2| extracted from the spectra (see text). The upper (lower) edge yields maximum interaction strength for vertical (horizontal) incident polarization. For polarization states varying from diagonal to circular, nearly constant interaction strengths at the individual edges are observed. At the corner, the associated change of relative phase of the interactions |g₁| and |g₂| leads to a strong modulation in |g_tot|, demonstrating the coherent actions of g₁ and g₂. f, Illustration of the three different measurement positions leading to single (red, blue circles) and double interaction (purple).

To demonstrate a modulation of the total coupling constant g_tot by mere manipulation of the relative phase of the interactions g₁ and g₂, we vary the incident polarization state in such a way as to keep the projections onto the vertical (∼|g₁|) and horizontal (∼|g₂|) axes fixed. This is the case for all elliptical polarization states with main axes rotated by 45° with respect to the edges, including ±45° linear as well as left- and right-hand circular polarizations. Figure 2c, d displays the nearly constant coupling strengths at the individual edges resulting from this pure phase variation. Placing the beam at the corner, however, such that it sequentially interacts with both near-fields, we find a strong change in the spectral width of the final electronic state after a variation through the same set of polarization states (Fig. 2e). This conclusively demonstrates the quantum coherence and thus reversibility of the two subsequent interactions. Specifically, a strong recompression of the spectrum is achieved near θ = 39°. In the spatial wavefunction picture, this corresponds to a cancellation of the initially imprinted phase modulation by the second interaction. The effect of sequential coherent interactions can also be illustrated by spatial maps, in which the total coupling constant is displayed as a function of beam position near the nanostructure (Fig. 1d). The individual edges exhibit largely homogeneous coupling constants decaying over a distance of about 100 nm away from the edge (orange regions). In addition, for a destructive relative phase of the individual interactions, a substantially reduced total coupling constant is evident near the corner, at which the electrons traverse both near-fields (green dashed circle).

To identify the individual near-field responses, we map the interaction strength for arbitrary incident polarization states by a systematic variation of both wave plate angles. Figure 3a displays the measured coupling constants g₁, g₂ and g_tot, with higher-resolved lineouts in Fig. 3c, d (symbols). For the individual edges (left and middle in Fig. 3a, red and blue symbols in Fig. 3c, d), we obtain quasi-polarizabilities α_1,2 = α_1,2n_1,2 with the normalized projection vectors and , close to the design aim of and , and amplitude prefactors of α₁ = 35 (V nm⁻¹)⁻¹ and α₂ = 44 (V nm⁻¹)⁻¹. The arbitrary overall phase of both vectors was chosen to yield real values for the respective dominant element. While the vectors n_1,2 are universal and spatially independent for each of the edges, the specific prefactor sensitively depends on the particular distance from the respective surface. Employing amplitudes α₁ = 52 (V nm⁻¹)⁻¹, α₂ = 29 (V nm⁻¹)⁻¹ and a constant phase offset ϕ₀ = 1.30, the entire set of measurements near the corner of the structure is successfully described by a summation $g_{\text{tot}}=({\alpha }_1+{\text{e}}^{i{\phi }_0}\times {\alpha }_2)‧J$, again clearly demonstrating the phase-controlled quantum coherent interaction with both near-fields. Minor deviations, for example in the incomplete spectral recompression near the minima of g_tot, are attributed to a spatial average over near-field strengths across the electron beam (see Methods ‘Determination of coupling constant and spatial averaging’). This leads to small residual sideband populations and highlights the importance of carrying out such experiments with low-emittance electron beams, as performed here, using nanotip sources. Dispersive reshaping of the wavefunction, on the other hand, can be excluded for the given spatial separation of the interaction planes (see Methods ‘Influence of dispersion’).

Figure 3: Demonstration of coherent dual interaction for arbitrary polarization states.

a, Coupling constant from experimental electron energy spectra measured for individual (left, middle) and combined (right) near-field actions. b, Corresponding simulations employing experimentally determined near-field responses α_1,2 (left, middle) and their coherent sum (right). Yellow star: settings for raster scan in Fig. 1d. c,d, Higher-resolved lineouts of experimental coupling constant |g| (symbols) and model prediction (solid lines). The position of the lineouts are indicated by dashed and solid lines in b.

A comment should be made about the invoked phase offset ϕ₀. The precise polarization state, at which maximum recompression occurs, is governed by the phase relation between the optical far-field and the respective near-fields, and the phase lag arising from the electron and light propagation between the two interaction planes. Although these phases are physically distinct, in practice, they can be combined in the single phase offset ϕ₀, which is sufficient to account for all experiments. For the present measurements, we identify this phase with a precision that corresponds to a timing uncertainty of a few attoseconds. This implies a sensitivity of the scheme to phase or timing changes to the free-electron wavefunction of this very same magnitude, rendering the presented interferometer an ideal tool to study excitation-induced phase shifts in new forms of electron holography employing the longitudinal degree of freedom. Utilizing this approach to imprint phase information onto the electron wavefunction could be translated to attosecond temporal resolution by, for example, energy-resolved electron diffraction.

Whereas the present work considers the longitudinal momentum, the transverse momentum component can also be accessed in coherent control experiments, for example, by multiple Kapitza–Dirac interactions³⁴ or diffraction from surface plasmon waves³⁵. Similarly, coupling to both transverse momentum components will allow for the optical preparation of free-electron angular momentum states in chiral near-fields³⁶. More generally, the absence of efficient decoherence mechanisms in vacuum renders free-electron wave packets an ideal system for coherent control schemes, which can be extended to multi-colour approaches and additional interaction stages. Future experiments may utilize this type of ‘electron–light interferometer’ by inserting optically excited materials in the gap for precision measurements of electronic dephasing with sub-cycle resolution. Various further applications include phase-resolved near-field imaging, possible quantum computation schemes using free electrons, or the tailored structuring of electron densities in accelerator beamlines with attosecond accuracy.

Methods

The experiments were performed in a recently developed ultrafast transmission electron microscope, featuring a nanoscale photoemitter as a pulsed electron source for electron pulses with high spatial coherence. Specifically, ultrashort electron pulses are generated by localized photoemission from a ZrO/W tip emitter, accelerated to a kinetic energy of 120 keV and focused tightly (with a beam divergence of 5.3 mrad) in close vicinity to a nanostructure. Electron spot diameters down to 3 nm and pulse durations as short as 300 fs were achieved. A scanning electron micrograph of the nanostructure design is shown in Fig. 1b. The two plates with a distance of 5 μm were milled by a focused ion beam from a single, annealed gold wire (30 μm diameter). The experimental scenario is sketched in Fig. 1c: a pump laser beam (800 nm wavelength, dispersively stretched to a pulse duration of 3.4 ps, 250 kHz repetition rate, 23 mW average power) passes a half- and a quarter-wave plate for polarization control and is focused onto the sample to a spot diameter of about 50 μm (full-width at half-maximum). The electron kinetic energy spectra are recorded with an electron energy loss spectrometer.

Sinusoidal phase modulation.

To obtain the electron wavefunction ψ(z, t) after interaction with the optical near-fields, we apply the scattering (S-matrix) approach in the interaction picture (see also ref. 7). The final wavefunction is given by |ψ(z, ∞)〉 = S| ψ(z, −∞)〉 with the time-ordered unitary operator

and the interaction Hamiltonian

where v is the electron velocity and e is the electron charge. The vector potential A(z, t) for the two near-fields separated by the distance L is given by

ϕ denotes the phase lag of the second near-field induced by the optical path length difference of the driving laser field (corresponding to d_l in Supplementary Fig. 2). For the wavefunction after interaction we obtain

In the second step, we introduced the coupling constant g = e/2ℏω∫ _−∞^∞F(z)exp(−iΔkz)dz, as in ref. 23. It is proportional to the spatial Fourier component of the longitudinal vector component of the near-field F(z) along the electron trajectory at the spatial frequency Δk = ω/v, which corresponds to the momentum change of an electron at velocity v gaining or losing an energy ℏω. Equation (7) evidences that the interaction of the free electrons with the two optical near-fields is describable as a single sinusoidal phase modulation of the electron wavefunction and that the two consecutive interactions coherently add up in the way stated in equation (3) in the main text.

Influence of dispersion.

Between the two interaction regions, the electron wavefunction propagates in free space. The momentum-dependent propagation operator is given by

where γ is the Lorentz factor and Δp is the momentum change due to the interaction with the optical near-field, with Δp given by Nℏω/v for the Nth-order sideband. During free propagation, the sideband orders acquire different phases, which leads to a dispersive reshaping of the electron wavefunction and, at a certain propagation distance, to a temporal focusing into a train of attosecond pulses⁷. In the present study, the propagation distance is much shorter than the distance to the temporal focus (typically millimetre scale). Specifically, the experimental parameters employed here (coupling constants g ≈ 5, propagation distance L = 6 μm, v = 0.6c, γ = 1.24) yield very small sideband-dependent phase shifts on the order of N² ⋅ 0.17 mrad, such that dispersive effects are negligible.

Coordinate system and geometric phase offset.

The angles θ and ξ define the orientation of the fast axes of the wave plates relative to the horizontal x axis of the coordinate system, which is indicated by black arrows in Supplementary Fig. 1a. The wave plate setting θ = ξ = −45°, for example, yields linear laser polarization at −45° to the x axis.

In the following, we discuss the influence of the sample and beam geometry on the constant phase offset ϕ₀. The difference in electron group and laser phase velocity leads to a phase lag, which can be calculated as follows: for a given plate distance d, the electron and laser path lengths are d_e = d/cosα and d_l = dcosβ/cosα, respectively, where α = 37° is the sample tilt angle and β = 55° is the angle between laser and electron beam. The path length difference corresponds to a timing difference of

with v = 0.6c. A small variation of α by about 2.4° shifts Δt by a quarter laser period, that is, ϕ₀ by 90°. Sample tilting thus presents a convenient way to externally control ϕ₀. Note that the data displayed in Figs 2e and 3c in the main text were recorded at two slightly different sample tilts, resulting in a relative phase shift of Δϕ = 81.5°.

Determination of coupling constant and spatial averaging.

In principle, the coupling constants can be inferred from the cutoff energy of the electron energy spectra, which is given by 2 |g| ℏω (ref. 7). For a more precise determination, we extracted coupling constants from a fit of Bessel amplitudes to the data, according to equation (1). Due to the finite electron beam size, a small spatial average over different coupling constants needs to be taken into account, for which we adopt a Gaussian distribution of the electron intensity in the beam. At the gold edges, the near-field strength can be regarded as homogeneous in directions parallel to an edge, and exponentially decaying along the perpendicular direction (see Supplementary Fig. 2g). In this case, the probability distribution of coupling constants is given as

where g₀ is the expectation value of the coupling constant, l is the decay length of the near-field strength and Σ is the electron beam width (standard deviation). For the analysis, we consider a constant ratio l/Σ for each near-field.

When averaging is taken into account, the experimental data are well reproduced. A comparison of Supplementary Figs 2c, e illustrates that spatial averaging only weakly affects the visibility of quantum coherent features in the electron energy spectra (see ref. 7). The spectra recorded at the upper edge show stronger averaging compared with the lower edge, since the electron focus is not perfectly centred between the two edges (small displacement Δz). For the data set shown here, we obtain l/Σ_U ≈ 5 and l/Σ_L ≈ 10. Together with the near-field decay length of l ≈ 90 nm (determined from the raster scan in Fig. 1d), we find Σ_U = 18 nm and Σ_L = 9 nm, in accordance with the electron focal spot diameter of 8 nm used in the experiment.

Data availability.

The data that support the plots within this paper and other findings of this study are available from the corresponding authors on request.