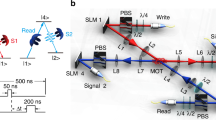
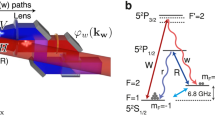
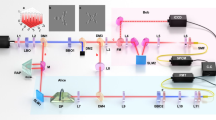
Abstract
Among the optical degrees of freedom, the orbital angular momentum of light1 provides unique properties2, including mechanical torque action, which has applications for light manipulation3, enhanced sensitivity in imaging techniques4 and potential high-density information coding for optical communication systems5. Recent years have also seen a tremendous interest in exploiting orbital angular momentum at the single-photon level in quantum information technologies6,7. In pursuing this endeavour, we demonstrate here the implementation of a quantum memory8 for quantum bits encoded in this optical degree of freedom. We generate various qubits with computer-controlled holograms, store and retrieve them on demand using a dynamic electromagnetically induced transparency protocol. We further analyse the retrieved states by quantum tomography and thereby demonstrate fidelities exceeding the classical benchmark, confirming the quantum functioning of our storage process. Our results provide an essential capability for future networks9 exploring the promises of orbital angular momentum of photons for quantum information applications.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Allen, L., Barnett, S. M. & Padgett, M. J. (eds) Optical Angular Momentum (IOP Publishing, 2003).
Torres, J. P. & Torner, L. Twisted Photons: Applications of Light With Orbital Angular Momentum (Wiley-VCH, 2011).
Grier, D. G. A revolution in optical manipulation. Nature 424, 810–816 (2003).
Uribe-Patarroyo, N., Fraine, A., Simon, D. S., Minaeva, O. & Sergienko, A. V. Object identification using correlated orbital angular momentum states. Phys. Rev. Lett. 110, 043601 (2013).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nature Photon. 6, 488–496 (2012).
Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001).
Leach, J., Padgett, M. J., Barnett, S. M., Franke-Arnold, S. & Courtial, J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 88, 257901 (2002).
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nature Photon. 3, 706–714 (2009).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Gröblacher, S., Jennewein, T., Vaziris, A., Weihs, G. & Zeilinger, A. Experimental quantum cryptography with qutrits. New J. Phys. 8, 75 (2006).
Langford, N. K. et al. Measuring entangled qutrits and their use for quantum bit commitment. Phys. Rev. Lett. 93, 053601 (2004).
Molina-Terriza, G., Vaziri, A., Ursin, R. & Zeilinger, A. Experimental quantum coin tossing. Phys. Rev. Lett. 94, 040501 (2005).
Dada, A. C., Leach, J., Buller, G. S., Padgett, M. J. & Andersson, E. Experimental high-dimensional two-photon entanglement and violations of generalized Bell inequalities. Nature Phys. 7, 677–680 (2011).
Fickler, R. et al. Quantum entanglement of high angular momenta. Science 338, 640–643 (2012).
Inoue, R. et al. Entanglement of orbital angular momentum states between an ensemble of cold atoms and a photon. Phys. Rev. A 74, 053809 (2006).
Pugatch, R., Shuker, M., Firstenberg, O., Ron, A. & Davidson, N. Topological stability of optical vortices. Phys. Rev. Lett. 98, 203601 (2007).
Moretti, D., Felinto, D. & Tabosa, J. W. R. Collapses and revivals of stored orbital angular momentum of light in a cold-atom ensemble. Phys. Rev. A 79, 023825 (2009).
Veissier, L. et al. Reversible optical memory for twisted photons. Opt. Lett. 38, 712–714 (2013).
Ding, D.-S., Zhou, Z.-Y., Shi, B.-S. & Guo, G.-G. Single-photon level quantum image memory based on cold atomic ensembles. Nature Commun. 4, 2527 10.1038/ncomms3527(2013).
Choi, K. S., Deng, H., Laurat, J. & Kimble, H. J. Mapping photonic entanglement into and out of a quantum memory. Nature 452, 67–71 (2008).
Specht, H. P. et al. A single-atom quantum memory. Nature 473, 190–193 (2011).
Gündoğan, M., Ledingham, P. M., Almasi, A., Cristiani, M. & de Riedmatten, H. Quantum storage of a photonic polarization qubit in a solid. Phys. Rev. Lett. 108, 190504 (2012).
Clausen, C., Bussières, F., Afzelius, M. & Gisin, N. Quantum storage of heralded polarization qubits in birefringent and anisotropically absorbing materials. Phys. Rev. Lett. 108, 190503 (2012).
Zhou, Z.-Q., Lin, W.-B., Yang, M., Li, C.-F. & Guo, G.-C. Realization of reliable solid-state quantum memory for photonic polarization qubit. Phys. Rev. Lett. 108, 190505 (2012)
Hau, L. V., Harris, S. E., Dutton, Z. & Behroozi, C. H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 397, 594–598 (1999).
Liu, C., Dutton, Z., Behroozi, C. H. & Hau, L. V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409, 490–493 (2001).
Vaziri, A., Weihs, G. & Zeilinger, A. Superpositions of the orbital angular momentum for applications in quantum experiments. J. Opt. B 4, S47 (2002).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Massar, S. & Popescu, S. Optimal extraction of information from finite quantum ensembles. Phys. Rev. Lett. 74, 1259–1263 (1995).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011).
Dudin, Y. O., Li, L. & Kuzmich, A. Light storage on the time scale of a minute. Phys. Rev. A 87, 031801(R) (2013).
Grodecka-Grad, A., Zeuthen, E. & Sørensen, A. S. High-capacity spatial multimode quantum memories based on atomic ensembles. Phys. Rev. Lett. 109, 133601 (2012).
Acknowledgements
The authors thank A. Zeilinger and R. Fickler for providing fork holograms and M.J. Padgett and D. Tasca for their assistance with the SLM. The authors also thank M. Scherman and S. Burks for their valuable contributions in the early stage of the experiment. This work is supported by the ERA-Net CHIST-ERA (QScale), the ERA-Net.RUS (Nanoquint), the Institut Francilien de Recherche sur les Atomes Froids (IFRAF) and by the European Research Council (ERC; starting grant HybridNet). A.N. acknowledges support from the Direction Générale de l'Armement (DGA). J.L. is a member of the Institut Universitaire de France.
Author information
Authors and Affiliations
Contributions
L.G., L.V., E.G. and J.L. planned the initial experimental set-up for light–matter interfacing, which was constructed by L.G., L.V. and J.L. All authors contributed to the OAM experiment. A.N., L.V. and D.M. designed the generation and characterization system and performed the measurements and data analysis under the supervision of J.L. All authors contributed to discussing the results. J.L., A.N., L.V. and D.M. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 644 kb)
Rights and permissions
About this article
Cite this article
Nicolas, A., Veissier, L., Giner, L. et al. A quantum memory for orbital angular momentum photonic qubits. Nature Photon 8, 234–238 (2014). https://doi.org/10.1038/nphoton.2013.355
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2013.355
This article is cited by
-
Polarization-Encoded Structured Light Generation Based on Holographic Metasurface
Plasmonics (2023)
-
Cosine-type apodized spiral zone plate to handle the topological charge of a vortex beam
Optical and Quantum Electronics (2023)
-
An integrated photonic circuit for color qubit preparation by third-order nonlinear interactions
Scientific Reports (2022)
-
Spontaneous generation and active manipulation of real-space optical vortices
Nature (2022)
-
Satellite-based continuous-variable quantum key distribution under the Earth’s gravitational field
Quantum Information Processing (2022)