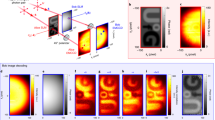
Abstract
The spatial structure of single photons1,2,3 is becoming an extensively explored resource to facilitate free-space quantum communication4,5,6,7 and quantum computation8 as well as for benchmarking the limits of quantum entanglement generation3 with orbital angular momentum modes1,9 or reduction of the photon free-space propagation speed10. Although accurate tailoring of the spatial structure of photons is now routinely performed using methods employed for shaping classical optical beams3,10,11, the reciprocal problem of retrieving the spatial phase-amplitude structure of an unknown single photon cannot be solved using complementary classical holography techniques12,13 that are known for excellent interferometric precision. Here, we introduce a method to record a hologram of a single photon that is probed by another reference photon, on the basis of a different concept of the quantum interference between two-photon probability amplitudes. As for classical holograms, the hologram of a single photon encodes the full information about the photon's ‘shape’ (that is, its quantum wavefunction) whose local amplitude and phase are retrieved in the demonstrated experiment.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Molina-Terriza, G., Torres, J. P. & Torner, L. Twisted photons. Nature Phys. 3, 305–310 (2007).
Lundeen, J. S., Sutherland, B., Patel, A., Stewart, C. & Bamber, C. Direct measurement of the quantum wavefunction. Nature 474, 188–191 (2011).
Fickler, R. et al. Quantum entanglement of high angular momenta. Science 338, 640–643 (2012).
Walborn, S. P., Lemelle, D. S., Almeida, M. P. & Ribeiro, P. H. S. Quantum key distribution with higher-order alphabets using spatially encoded qudits. Phys. Rev. Lett. 96, 090501 (2006).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nature Photon. 6, 488–496 (2012).
Vallone, G. et al. Free-space quantum key distribution by rotation-invariant twisted photons. Phys. Rev. Lett. 113, 060503 (2014).
Krenn, M., Handsteiner, J., Fink, M., Fickler, R. & Zeilinger, A. Twisted photon entanglement through turbulent air across Vienna. Proc. Natl Acad. Sci. USA 112, 14197–14201 (2015).
Abouraddy, A. F., Di Giuseppe, G., Yarnall, T. M., Teich, M. C. & Saleh, B. E. A. Implementing one-photon three-qubit quantum gates using spatial light modulators. Phys. Rev. A 86, 050303 (2012).
Nagali, E. et al. Optimal quantum cloning of orbital angular momentum photon qubits through Hong–Ou–Mandel coalescence. Nature Photon. 3, 720–723 (2009).
Giovannini, D. et al. Spatially structured photons that travel in free space slower than the speed of light. Science 347, 857–860 (2015).
Dholakia, K. & Čižmár, T. Shaping the future of manipulation. Nature Photon. 5, 335–342 (2011).
Gabor, D. A new microscopic principle. Nature 161, 777–778 (1948).
Collier, R. J., Burckhardt, C. B. & Lin, L. H. Optical Holography (Academic, 1971).
Lvovsky, A. I. et al. Quantum state reconstruction of the single-photon Fock state. Phys. Rev. Lett. 87, 050402 (2001).
Smith, B. J., Killett, B., Raymer, M. G., Walmsley, I. a. & Banaszek, K. Measurement of the transverse spatial quantum state of light at the single-photon level. Opt. Lett. 30, 3365–3367 (2005).
Mirhosseini, M., Magaña-Loaiza, O. S., Hashemi Rafsanjani, S. M. & Boyd, R. W. Compressive direct measurement of the quantum wave function. Phys. Rev. Lett. 113, 090402 (2014).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Jachura, M. & Chrapkiewicz, R. Shot-by-shot imaging of Hong-Ou-Mandel interference with an intensified sCMOS camera. Opt. Lett. 40, 1540–1543 (2015).
Kaltenbaek, R., Blauensteiner, B., Żukowski, M., Aspelmeyer, M. & Zeilinger, A. Experimental interference of independent photons. Phys. Rev. Lett. 96, 240502 (2006).
Patel, R. B. et al. Two-photon interference of the emission from electrically tunable remote quantum dots. Nature Photon. 4, 632–635 (2010).
Bennett, A. J., Patel, R. B., Nicoll, C. A., Ritchie, D. A. & Shields, A. J. Interference of dissimilar photon sources. Nature Phys. 5, 715–717 (2009).
Servin, M., Marroquin, J. L. & Cuevas, F. J. Demodulation of a single interferogram by use of a two-dimensional regularized phase-tracking technique. Appl. Opt. 36, 4540–4548 (1997).
Walmsley, I. A. & Dorrer, C. Characterization of ultrashort electromagnetic pulses. Adv. Opt. Photon. 1, 308–437 (2009).
Specht, H. P. et al. Phase shaping of single-photon wave packets. Nature Photon. 3, 469–472 (2009).
Beduini, F. A., Zielińska, J. A., Lucivero, V. G., de Icaza Astiz, Y. A. & Mitchell, M. W. Interferometric measurement of the biphoton wave function. Phys. Rev. Lett. 113, 183602 (2014).
Polycarpou, C., Cassemiro, K. N., Venturi, G., Zavatta, A. & Bellini, M. Adaptive detection of arbitrarily shaped ultrashort quantum light states. Phys. Rev. Lett. 109, 053602 (2012).
Wasilewski, W., Kolenderski, P. & Frankowski, R. Spectral density matrix of a single photon measured. Phys. Rev. Lett. 99, 123601 (2007).
Lopes, R. et al. Atomic Hong–Ou–Mandel experiment. Nature 520, 66–68 (2015).
Chrapkiewicz, R., Wasilewski, W. & Banaszek, K. High-fidelity spatially resolved multiphoton counting for quantum imaging applications. Opt. Lett. 39, 5090–5093 (2014).
Peeters, W., Renema, J. & van Exter, M. Engineering of two-photon spatial quantum correlations behind a double slit. Phys. Rev. A 79, 043817 (2009).
Bennink, R. S., Bentley, S. J., Boyd, R. W. & Howell, J. C. Quantum and classical coincidence imaging. Phys. Rev. Lett. 92, 033601 (2004).
Morris, P. A., Aspden, R. S., Bell, J. E. C., Boyd, R. W. & Padgett, M. J. Imaging with a small number of photons. Nature Commun. 6, 5913 (2015).
Fickler, R., Krenn, M., Łapkiewicz, R., Ramelow, S. & Zeilinger, A. Real-time imaging of quantum entanglement. Sci. Rep. 3, 1914 (2013).
Rozema, L. a. et al. Scalable spatial superresolution using entangled photons. Phys. Rev. Lett. 112, 223602 (2014).
Allman, M. S. et al. A near-infrared 64-pixel superconducting nanowire single photon detector array with integrated multiplexed readout. Appl. Phys. Lett. 106, 192601 (2015).
John, J. J. et al. PImMS, a fast event-triggered monolithic pixel detector with storage of multiple timestamps. J. Instrum. 7, C08001 (2012).
Just, F. et al. Detection of non-classical space-time correlations with a novel type of single-photon camera. Opt. Express 22, 17561–17572 (2014).
Acknowledgements
We acknowledge insightful comments and discussion about the work and the manuscript with M. Barbieri, R. Łapkiewicz, M.J. Padgett and A. Zeilinger. This project was financed by the National Science Centre (grant no. DEC-2013/09/N/ST2/02229 and DEC-2011/03/D/ST2/01941). R.C. was supported by Foundation for Polish Science. M.J and K.B. were supported by the European Commission under the Seventh Framework Programme for Research and Technological Development integrated project Simulations and Interfaces with Quantum Systems (grant agreement no. 600645) co-financed by the Polish Ministry of Science and Higher Education.
Author information
Authors and Affiliations
Contributions
W.W. proposed the idea of wavefunction phase retrieval. R.C. designed and programmed the experiment, developed HSP methods, analysed the data and prepared figures. M.J. built the set-up and performed the measurements. R.C. and M.J. wrote the manuscript assisted by W.W. and K.B, who supervised the work and contributed to data analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1691 kb)
Rights and permissions
About this article
Cite this article
Chrapkiewicz, R., Jachura, M., Banaszek, K. et al. Hologram of a single photon. Nature Photon 10, 576–579 (2016). https://doi.org/10.1038/nphoton.2016.129
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2016.129
This article is cited by
-
Coincidence imaging for Jones matrix with a deep-learning approach
npj Nanophotonics (2024)
-
Applications of single photons in quantum metrology, biology and the foundations of quantum physics
Nature Reviews Physics (2023)
-
Mathematical Models of Photons
Foundations of Physics (2023)
-
Pixel super-resolution with spatially entangled photons
Nature Communications (2022)
-
Quantum microscopy based on Hong–Ou–Mandel interference
Nature Photonics (2022)