Abstract
Quantum phenomena such as entanglement can improve fundamental limits on the sensitivity of a measurement probe. In optical interferometry, a probe consisting of N entangled photons provides up to a \(\sqrt{N}\) enhancement in phase sensitivity compared to a classical probe of the same energy. Here, we employ high-gain parametric down-conversion sources and photon-number-resolving detectors to perform interferometry with heralded quantum probes of sizes up to N = 8 (i.e. measuring up to 16-photon coincidences). Our probes are created by injecting heralded photon-number states into an interferometer, and in principle provide quantum-enhanced phase sensitivity even in the presence of significant optical loss. Our work paves the way toward quantum-enhanced interferometry using large entangled photonic states.
Similar content being viewed by others
Introduction
Optical interferometry provides a means to sense very small changes in the path of a light beam. These changes may be induced by a wide range of phenomena, from pressure and temperature variations that impact refractive index, to modifications of the space-time metric that characterize gravitational waves. In its simplest form, interferometry measures distortions via the phase difference ϕ between the two paths of the interferometer. The uncertainty Δϕ in a measurement of this phase difference is limited fundamentally by the quantum noise of the illuminating light beams. This noise can be reduced by employing light exhibiting nonclassical properties such as entanglement and squeezing in order to improve the sensitivity of an interferometer beyond classical limits1. Quantum states of light are most effective when it is desirable to maximize the phase sensitivity per photon inside an interferometer, such as in gravitational wave detectors2,3 or when characterizing delicate photosensitive samples4,5,6,7,8.
In principle, N-photon quantum states of light such as the highly entangled N00N state can provide up to a \(\sqrt{N}\) precision enhancement over a classical state of equal energy9,10,11,12,13,14,15,16,17. Unfortunately these highly entangled states are vulnerable to decoherence, especially at large photon numbers. In practice, their enhanced sensitivity disappears in the presence of loss which may originate from interactions inside the interferometer (e.g. absorption in a sample) as well as external losses in the state preparation and detection18.
Although a \(\sqrt{N}\) enhancement is not achievable in the presence of loss, one can engineer states that trade-away sensitivity for loss-tolerance in order to still achieve some advantage over classical limits19,20. For example, squeezed light21,22,23,24 and non-maximally entangled states such as Holland-Burnett states25,26,27,28,29,30,31 can surpass classical limits despite some losses. Importantly, the precision enhancement achievable with such states can grow with N, even in the presence of loss19. Experimental demonstrations have prepared unheralded N = 629,30 (or heralded N = 228) Holland-Burnett states, but further increase of N is constrained by source brightness as well as detector efficiency and number-resolution. This motivates developing experimental protocols that can produce and detect loss-tolerant states with larger photon numbers.
In this work, we address a number of key challenges in order to scale-up quantum-enhanced interferometry using definite photon-number states of light. Firstly, we introduce probe states that are prepared by combining two photon-number states on a beam splitter similarly to Holland-Burnett states. However, unlike the latter, we allow the initial photon-number states to be unequal. We show that these generalized Holland-Burnett states are more sensitive than both Holland-Burnett and N00N states in the presence of loss and approximate the performance of the optimal probe19. Secondly, we experimentally implement our scheme using high-gain parametric down-conversion sources32,33 and state-of-the-art photon-number-resolving detectors34 in order to access a large photon-number regime. We herald entangled probes of sizes up to N = 8 and measure up to 16-photon coincidences, thereby further increasing the scale of experimental multiphoton quantum technologies35,36,37.
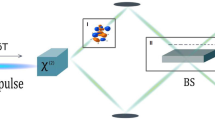
The idea is illustrated in Fig. 1a. Two type-II parametric down-conversion (PDC) sources each produce pairs of light beams that are quantum-correlated in photon number, i.e. a two-mode squeezed vacuum state
Here, λ is a parameter that determines the average number of photons in each beam, 〈n〉 = λ2/(1 − λ2). Measuring one of the beams with an ideal lossless photon-number-resolving detector projects the second beam onto a known photon-number state \(\left|{h}_{1}\right\rangle\). Duplicating this procedure with a second independent source and detector, we herald pairs of photon-number states that are not necessarily identical, i.e. the probe \(\left|{h}_{1},{h}_{2}\right\rangle\). When these states are combined on the first beam splitter, multiphoton interference generates a path-entangled probe inside the interferometer38.
a Two type-II parametric down-conversion sources each produce orthogonally-polarized pairs of beams that are separated using polarizing beam splitters. By measuring one of the beams from each source with a photon-number-resolving detector, we herald a pair of photon-number states \(\left|{h}_{1},{h}_{2}\right\rangle\). We inject this probe into an interferometer and perform photon counting at the output to estimate the unknown phase difference ϕ. b Quantum Fisher information \({\mathcal{Q}}\) calculated for 8-photon (N = h1 + h2 = 8) probes inside the interferometer as a function of the signal transmissivity ηs which is assumed to be equal in both interferometer modes. Coloured curve in the main figure plots \({\mathcal{Q}}\) of the probe with the optimal Δ = ∣h1 − h2∣ for a given ηs, while the inset shows the full curves of each probe for ηs ∈ [0.4, 0.75]. Our probe approximates the performance of the optimal state [black line] and surpasses that of the N00N state [dashed line] for efficiencies below ~90%. The gray filled region indicates performance below the shot-noise limit.
We quantify the phase-sensitivity of the probe inside the interferometer by calculating the quantum Fisher information \({\mathcal{Q}}\). The quantity \({\mathcal{Q}}\) provides a lower limit on the best achievable phase uncertainty via the quantum Cramer-Rao bound, \(\Delta \phi \ge 1/\sqrt{{\mathcal{Q}}}\). The bound can be saturated using the optimal measurement strategy, which in the absence of loss is photon counting for the probes considered here39,40.
In Fig. 1b, we plot \({\mathcal{Q}}\) for several probes with the same total photon number N = h1 + h2 = 8, but different Δ = ∣h1 − h2∣, as a function of the signal transmissivity ηs which we assume to be equal in both interferometer modes. Probes with a small Δ provide a greater advantage over the classical shot-noise limit but are more sensitive to losses. Since the probe is heralded in our scheme, one can choose the optimal Δ for a given ηs.
Also shown in Fig. 1b is \({\mathcal{Q}}\) for the optimal state that maximizes this parameter for a given N and ηs. This state has been found in ref. 19; the derivation is reproduced in the Supplementary Method 1. For the loss-free case (ηs = 1), the optimal state is the N00N state. However, for efficiencies below ~90%, our probes significantly surpass the N00N state in terms of \({\mathcal{Q}}\), exhibiting performance close to optimal. Moreover, in contrast to the N00N and Holland-Burnett states, our probe performs at least as well as the shot-noise limit for any amount of loss.
We now turn to the experiment. Both PDC sources are periodically poled potassium titanyl phosphate (ppKTP) waveguides pumped with ~0.5 ps long pulses from a mode-locked laser at a repetition rate of 100 kHz. The four detectors are superconducting transition edge sensors which we use to count up to 10 photons with a detection efficiency exceeding 95%34. The interferometer is a fiber-based device in which we can control the distance between two evanescently coupled fibers using a micrometer to vary ϕ, much like changing the path length difference between two arms of an interferometer. Further details on the experimental setup can be found in the Methods.
We measure interference fringes given by \({{\rm{pr}}}_{{s}_{1},{s}_{2},{h}_{1},{h}_{2}}(\phi )\), the joint photon-number probability per pump pulse to obtain the herald outcome (h1, h2) and measure (s1, s2) at the output of the interferometer when the phase difference is ϕ. We will refer to this as the (s1, s2, h1, h2) rate. To quantify the phase sensitivity of the rates measured with a particular herald outcome (h1, h2), we calculate the Fisher information:
where ∂ϕ denotes the partial derivative with respect to ϕ, and \({\tilde{{\rm{pr}}}}_{{s}_{1},{s}_{2},{h}_{1},{h}_{2}}(\phi )\) is a model fitted to the measured rates (see Supplementary Method 2). Note that \({{\mathcal{F}}}_{{h}_{1},{h}_{2}}(\phi )\) quantifies the amount of information about ϕ in our measurement results, i.e. for a specific measurement strategy, and so \({{\mathcal{F}}}_{{h}_{1},{h}_{2}}(\phi )\le {\mathcal{Q}}\). We compare the performance of our photon counting strategy to the optimal measurement strategy in the Supplementary Discussion 1.
Our primary figure of merit is the Fisher information per detected signal photon conditioned on measuring (h1, h2) at the heralding detectors,
where
is the total number of detected signal photons. Injecting a coherent state into our interferometer would in principle yield the Fisher information \({\mathcal{F}}=\langle \tilde{n}\rangle\) when the detected mean photon number is \(\langle \tilde{n}\rangle\)18. Thus, our figure of merit can be easily compared to the shot-noise limit which corresponds to \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )=1\).
We measured the total efficiency of both the heralding and signal modes to be between 47–55% (see Supplementary Method 3). This includes ~90% waveguide transmission, ~70% mode coupling efficiency into fibers, 90% interferometer transmission, and ≥95% detector efficiency. Due to the latter two losses, the detected \(\langle \tilde{n}\rangle\) is 10–15% smaller than the mean photon number inside the interferometer. As such, the Fisher information per photon inside the interferometer (which is the relevant resource when e.g. probing a delicate sample) is ~10–15% smaller than \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\).
Results
Low gain regime
We begin with low pump power to test our setup in the weak gain regime (λ ~ 0.25, 10 μW per source). In Fig. 2, we show results for two different probes, (a) \(\left|1,1\right\rangle\), the well-studied N = 2 N00N or Holland-Burnett state, and (b) \(\left|2,1\right\rangle\), a probe studied here for the first time. We calculate \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) using two methods. In the first, we discard events in which we know photons were lost by only including rates where s1 + s2 = h1 + h2 in the sums of Eqs. (2) and (3). These rates are shown in the top panels of Fig. 2. Using this first method, \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) [green curves] surpasses the shot-noise limit by 0.09 ± 0.01 for \(\left|1,1\right\rangle\) and 0.10 ± 0.04 for \(\left|2,1\right\rangle\) at its highest point. In the second method, we include all measured events. Note that this may include events where s1 + s2 < h1 + h2 due to loss in the signal modes, but also s1 + s2 > h1 + h2 due to loss in the herald modes. Conditioned on obtaining the herald outcome (h1, h2), the probability of the latter occurring can be minimized by reducing the pump power and hence λ. This increases the purity of the probe at the cost of reducing its heralding rate. Without post-selection, \(\tilde{{\mathcal{F}}}(\phi )\) [red curves] drops below the shot-noise limit mainly due to losses.
a Rates measured with the probe \(\left|1,1\right\rangle\): (s1, s2, h1, h2) = (2, 0, 1, 1) [blue], (1, 1, 1, 1) [orange], (0, 2, 1, 1) [green]. b Rates measured with the probe \(\left|2,1\right\rangle\): (3, 0, 2, 1) [blue], (2, 1, 2, 1) [orange], (1, 2, 2, 1) [green], (0, 3, 2, 1) [red]. Error bars are one standard deviation assuming Poissonian counting statistics. Lines are a model fitted to \({{\rm{pr}}}_{{s}_{1},{s}_{2},{h}_{1},{h}_{2}}(\phi )\). Bottom panels show the normalized Fisher information \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) calculated using two methods: (i) post-selecting on events where s1 + s2 = h1 + h2 [green] and (ii) using all events [red]. Line thicknesses show 1σ confidence intervals obtained by fitting 50 simulated data sets that are calculated with a Monte Carlo method. The dashed black line indicates the shot-noise limit.
In addition to loss, the spectral purity and distinguishability of our photons are also sources of imperfection that reduce the contrast of the fringes and hence diminish \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\)41. Consider the probe \(\left|1,1\right\rangle\), for example. For ϕ = ±π/2, the whole interferometer acts as a balanced beam splitter, in which case Hong-Ou-Mandel interference should lead to a complete suppression in coincidences at its output. However, as can be seen in the orange (1, 1, 1, 1) fit in Fig. 2a, the visibility of this interference effect is ~75%. This visibility exceeds \(\sqrt{0.5}\), which is the minimum required for demonstrating post-selected quantum-enhanced sensitivity with the probe \(\left|1,1\right\rangle\)12,28,42. In addition to spectral mismatch between the signal modes, the visibility is degraded by uncorrelated background photons (~5% of detected photons) and the slight multi-mode nature of our sources, both of which reduce the purity of our heralded photons. We discuss source imperfections in more detail in the Supplementary Discussion 2. The finite detector energy resolution also plays a small role as the detectors have a ~1% chance to mislabel an event by ±1 photon43.
High gain regime
Next, we increase the pump power to reach a high gain regime (λ ~ 0.75, 135 μW per source) in which we can herald large photon numbers. We detect 16-photon events at a rate of roughly 7 per second, which is much higher than the state-of-the-art achievable with bulk crystal PDC sources36 or quantum dots37. In Fig. 3a, we plot \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) calculated without post-selection for all probes with N = 8. As expected given the amount of loss in our experiment, probes with larger Δ are more phase sensitive due to their increased robustness to loss [Fig. 1b]. In particular, the sensitivity of the Δ = N probe should be shot-noise limited regardless of losses44. However, in practice, the heralded detection of 0 photons could occur due to photon loss in the corresponding herald mode, resulting in the contamination of the signal with states for which Δ ≠ N. This degrades the performance of the Δ = 8 probe [orange curve]. In the Supplementary Discussion 3, we show that shot-noise limited performance with the Δ = N probe is recovered by blocking one of the sources.
a \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) of 8-photon probes (N = 8) parameterized by Δ = ∣h1 − h2∣. Curves are calculated using the data and Eqs. (2) and (3) without post-selection. Probes with a larger Δ have a larger \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) and hence greater phase sensitivity due to their increased robustness to loss. Line thicknesses show 1σ confidence intervals obtained by fitting 50 simulated data sets that are calculated with a Monte Carlo method. b, c Show a subset of rates for the probe with Δ = 8 and Δ = 0, respectively. Error bars are one standard deviation assuming Poissonian counting statistics. The lines are a model fitted to \({{\rm{pr}}}_{{s}_{1},{s}_{2},{h}_{1},{h}_{2}}(\phi )\).
Discussion
The fringes produced by our probes exhibit a number of different features compared to those measured with N00N or Holland-Burnett states. For example, with these two states, the expected signature of N-photon interference are fringe oscillations that vary as \(\cos (N\phi )\). While our measured fringes do not exhibit such oscillations in the high gain regime, they do exhibit sharper features than classical fringes. We show this explicitly by comparing our rates to those measured with distinguishable photons. This is achieved by temporally delaying photons coming from the top source with respect to photons coming from the bottom source by more than their coherence time. As an example, we consider the probe \(\left|3,2\right\rangle\) in Fig. 4. When the photons are injected inside the interferometer at the same time, the fringe contrast is significantly higher than when they are temporally delayed [Fig. 4a]. Likewise, when we calculate \({\tilde{{\mathcal{F}}}}_{3,2}(\phi )\) without post-selection, we find an improvement in the probe’s sensitivity in the former case [Fig. 4b]. This demonstrates that the probe sensitivity derives from multiphoton interference even at high photon numbers.
Benefits of multiphoton interference using the probe \(\left|3,2\right\rangle\). a Two sets of rates [blue: (5, 0, 3, 2), orange: (3, 2, 3, 2)] measured when the photons are injected inside the interferometer at the same time (data: circles, theory: bold lines) or at different times (data: crosses, theory: dashed line). In the latter case, the photons are well modelled by classical distinguishable particles. Error bars are one standard deviation assuming Poissonian counting statistics. b \({\tilde{{\mathcal{F}}}}_{3,2}(\phi )\) shows a significant improvement in sensitivity in the former case (bold line) compared to the latter case (dashed line), demonstrating that multiphoton interference improved the sensitivity of our probe. Red shaded regions shows 1σ confidence intervals obtained by fitting 50 simulated data sets that are calculated with a Monte Carlo method.
With any finite amount of loss, \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) vanishes when all fringes share a common turning point such as at ϕ = 0. In the case of Holland-Burnett (Δ = 0) and N00N states, there are also common turning points at ϕ = ±π/2 which causes the reduction in \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) around these phase values [Fig. 3c]. In contrast, the probes with Δ = 4, 6, 8 do not have a dip in \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\pm\! \pi /2)\). The origin of this effect for Δ = 8 can be seen directly in the rates shown in Fig. 3b. The region of the fringe with high sensitivity to ϕ (i.e. large gradient) is different for different values of ∣s1 − s2∣. This feature of \({\tilde{{\mathcal{F}}}}_{{h}_{1},{h}_{2}}(\phi )\) allows estimating ϕ without prior knowledge of the range in which it lies, as is required for N00N or Holland-Burnett states, and thus provides a means for global phase estimation without using an adaptive protocol27,45.
Finally, we briefly compare our results to other works reporting Fisher information per detected photon. The highest achieved here is ~1.1 using the herald outcome (2, 1), i.e. a N = 3 probe. Reference 31 and ref. 17, respectively, report ~1.25 and ~1.2 using a N = 2 probe. The latter work also achieves a Fisher information per photon inside the interferometer (i.e. accounting for undetected photons) of ~1.15 which thus far is the only experiment demonstrating an unconditional improvement to the shot-noise limit. In the Supplementary Discussion 4, we estimate that an efficiency of 80% (in all four modes) and quantum interference visibility of 85% would be sufficient to demonstrate an improvement to the shot-noise limit with N = 8 photons without post-selection. Although we do not attain these parameters in our experiment, our results do demonstrate the robustness of our probes to losses despite their large size. For example, the Fisher information per photon calculated without post-selection for the N = 8 probe with Δ = 6 [Fig. 3a] is slightly higher than that of the N = 2 N00N state [Fig. 2a]. This contradicts the usual expectation that large entangled probes will necessarily be more fragile to noise and loss.
In summary, we proposed and experimentally demonstrated a scheme for quantum-enhanced interferometry that exploits bright two-mode squeezed vacuum sources and photon-number-resolving detectors. We measured interference fringes involving up to 16 photons which is significantly higher than the previous state-of-the-art35,36. Crucially, our scheme prepares probes that are nearly optimally robust to losses and hence addresses one of the principal challenges when scaling-up to large entangled photonic states. With further improvements in the quality (e.g. coupling efficiency into optical fiber and purity) of bright two-mode squeezed vacuum sources compatible with transition edge sensors33,46, we believe our loss-tolerant scheme provides a promising route towards achieving quantum-enhanced resolution using large entangled photonic states.
Methods
Sources
We pick 150-fs pulses from a mode-locked Ti:Sapphire laser (Coherent Mira-HP) at a rate of 100 kHz using a Pockels-cell-based pulse picker having a 50 dB extinction ratio. This repetition rate is chosen to accommodate the recovery time of the transition edge sensor detectors. The pump pulses are filtered to 783 ± 2 nm [full-width at half maximum] using a pair of angle-tuned bandpass filters. We split the pulses into two paths that are matched in length using a translation stage. In each path, we pump a 8 mm long ppKTP waveguide that is phase-matched for type-II parametric down-conversion. At the exit of the waveguide, the pump light is rejected with a longpass filter, and the orthogonally-polarized down-converted modes are separated using a polarizing beam splitter. Each down-converted mode is filtered with a bandpass filter whose bandwidth is chosen to transmit the main feature of the down-converted spectrum but reject its side-lobes. The herald modes (1566 ± 7 nm) are coupled into single-mode fibers and sent directly to the detectors. The signal modes (1567 ± 7 nm) are coupled into polarization-maintaining single-mode fibers and sent into the interferometer. Details on the coupling efficiency and the spectral indistinguishability of the signal modes are provided in the Supplementary Discussion 2.
Interferometer
The interferometer is a fiber-based variable beam splitter (Newport F-CPL-1550-P-FP). The splitting ratio is adjusted by controlling the distance between two evanescently coupled fibers using a micrometer, which is analogous to changing the path length difference between two arms of an interferometer. In fact, any variable beam splitter that coherently splits light into two modes can be described by the same transformation as a Mach-Zender-type interferometer47.
During data acquisition, we scan the distance x between the two evanescently coupled fibers. To display our data as a function of the interferometer phase, we first calculate the transmission coefficient T(x) of the variable beam splitter using the measured (1, 0, 1, 0) and (0, 1, 1, 0) rates:
At low powers, we find that the quantity T(x) typically varies within [0.02, 0.98]. To obtain the corresponding phase, we correct for the imperfect visibility:
such that Tcorr(x) varies between [0, 1]. For a single photon injected into a Mach-Zender type interferometer with phase difference ϕ between its two arms, one expects \({T}_{{\rm{corr}}}(x)=[1-\cos (\phi )]/2\). Solving for ϕ, we find:
Detectors
Our detectors are superconducting transition edge sensor detectors that operate at a temperature of 85 mK inside a dilution refrigerator. Details on their physical operation can be found in ref. 34. An electrical trigger signal from the pump laser begins a 6 μs time window of data acquisition during which the detector outputs are amplified and recorded with an analogue-to-digital converter. We use a matched-filter technique in real-time to convert each detector’s output trace into a scalar value48. The scalar value is then converted into a photon number using bins that are set during an initial calibration run prior to data acquisition.
Data availability
The data sets generated and/or analyzed during this study are available from the corresponding author on reasonable request. Correspondence and requests for materials should be addressed to G.S.T.
References
Demkowicz-Dobrzański, R., Jarzyna, M. & Kołodyński, J. Quantum limits in optical interferometry. Progress in Optics, Vol. 60, 345–435 (Elsevier, 2015).
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D. 23, 1693–1708 (1981).
Tse, M. et al. Quantum-enhanced advanced LIGO detectors in the era of gravitational-wave astronomy. Phys. Rev. Lett. 123, 231107 (2019).
Crespi, A. et al. Measuring protein concentration with entangled photons. Appl. Phys. Lett. 100, 233704 (2012).
Wolfgramm, F., Vitelli, C., Beduini, F. A., Godbout, N. & Mitchell, M. W. Entanglement-enhanced probing of a delicate material system. Nat. Photonics 7, 28 (2013).
Taylor, M. A. et al. Biological measurement beyond the quantum limit. Nat. Photon. 7, 229 (2013).
Taylor, M. A. & Bowen, W. P. Quantum metrology and its application in biology. Phys. Rep. 615, 1–59 (2016).
Cimini, V. et al. Adaptive tracking of enzymatic reactions with quantum light. Opt. Express 27, 35245–35256 (2019).
Bollinger, J. J., Itano, W. M., Wineland, D. J. & Heinzen, D. J. Optimal frequency measurements with maximally correlated states. Phys. Rev. A 54, R4649–R4652 (1996).
Mitchell, M. W., Lundeen, J. S. & Steinberg, A. M. Super-resolving phase measurements with a multiphoton entangled state. Nature 429, 161–164 (2004).
Walther, P. et al. De Broglie wavelength of a non-local four-photon state. Nature 429, 158–161 (2004).
Nagata, T., Okamoto, R., O’Brien, J. L., Sasaki, K. & Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 316, 726–729 (2007).
Kim, H., Park, H. S. & Choi, S.-K. Three-photon N00N states generated by photon subtraction from double photon pairs. Opt. Express 17, 19720–19726 (2009).
Afek, I., Ambar, O. & Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 328, 879–881 (2010).
Matthews, J. C. F., Politi, A., Bonneau, D. & O’Brien, J. L. Heralding two-photon and four-photon path entanglement on a chip. Phys. Rev. Lett. 107, 163602 (2011).
Ulanov, A. E., Fedorov, I. A., Sychev, D., Grangier, P. & Lvovsky, A. Loss-tolerant state engineering for quantum-enhanced metrology via the reverse Hong–Ou–Mandel effect. Nat. Commun. 7, 11925 (2016).
Slussarenko, S. et al. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photonics 11, 700 (2017).
Datta, A. et al. Quantum metrology with imperfect states and detectors. Phys. Rev. A 83, 063836 (2011).
Dorner, U. et al. Optimal quantum phase estimation. Phys. Rev. Lett. 102, 040403 (2009).
Kacprowicz, M., Demkowicz-Dobrzański, R., Wasilewski, W., Banaszek, K. & Walmsley, I. Experimental quantum-enhanced estimation of a lossy phase shift. Nat. Photonics 4, 357 (2010).
Demkowicz-Dobrzański, R., Banaszek, K. & Schnabel, R. Fundamental quantum interferometry bound for the squeezed-light-enhanced gravitational wave detector GEO 600. Phys. Rev. A 88, 041802 (2013).
Lang, M. D. & Caves, C. M. Optimal quantum-enhanced interferometry using a laser power source. Phys. Rev. Lett. 111, 173601 (2013).
Yonezawa, H. et al. Quantum-enhanced optical-phase tracking. Science 337, 1514–1517 (2012).
Berni, A. A. et al. Ab initio quantum-enhanced optical phase estimation using real-time feedback control. Nat. Photon. 9, 577 (2015).
Holland, M. J. & Burnett, K. Interferometric detection of optical phase shifts at the Heisenberg limit. Phys. Rev. Lett. 71, 1355–1358 (1993).
Sun, F. et al. Experimental demonstration of phase measurement precision beating standard quantum limit by projection measurement. EPL 82, 24001 (2008).
Xiang, G.-Y., Higgins, B. L., Berry, D., Wiseman, H. M. & Pryde, G. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photonics 5, 43–47 (2011).
Thomas-Peter, N. et al. Real-world quantum sensors: Evaluating resources for precision measurement. Phys. Rev. Lett. 107, 113603 (2011).
Xiang, G., Hofmann, H. & Pryde, G. Optimal multi-photon phase sensing with a single interference fringe. Sci. Rep. 3, 2684 (2013).
Jin, R.-B. et al. Detection-dependent six-photon Holland-Burnett state interference. Sci. Rep. 6, 36914 (2016).
Matthews, J. C. et al. Towards practical quantum metrology with photon counting. npj Quantum Inf. 2, 1–7 (2016).
Eckstein, A., Christ, A., Mosley, P. J. & Silberhorn, C. Highly efficient single-pass source of pulsed single-mode twin beams of light. Phys. Rev. Lett. 106, 013603 (2011).
Harder, G. et al. Single-mode parametric-down-conversion states with 50 photons as a source for mesoscopic quantum optics. Phys. Rev. Lett. 116, 143601 (2016).
Lita, A. E., Miller, A. J. & Nam, S. W. Counting near-infrared single-photons with 95% efficiency. Opt. Express 16, 3032–3040 (2008).
Gao, W.-B. et al. Experimental demonstration of a hyper-entangled ten-qubit Schrödinger cat state. Nat. Phys 6, 331–335 (2010).
Wang, X.-L. et al. Experimental ten-photon entanglement. Phys. Rev. Lett. 117, 210502 (2016).
Wang, H. et al. Boson sampling with 20 input photons and a 60-mode interferometer in a 1014-dimensional Hilbert space. Phys. Rev. Lett. 123, 250503 (2019).
Stobińska, M. et al. Quantum interference enables constant-time quantum information processing. Sci. Adv. 5, eaau9674 (2019).
Hofmann, H. F. All path-symmetric pure states achieve their maximal phase sensitivity in conventional two-path interferometry. Phys. Rev. A 79, 033822 (2009).
Zhong, W., Huang, Y., Wang, X. & Zhu, S.-L. Optimal conventional measurements for quantum-enhanced interferometry. Phys. Rev. A 95, 052304 (2017).
Birchall, P. M., Sabines-Chesterking, J., O’Brien, J. L., Cable, H. & Matthews, J. C. Beating the shot-noise limit with sources of partially-distinguishable photons. arXiv preprint https://arxiv.org/abs/1603.00686 (2016).
Resch, K. J. et al. Time-reversal and super-resolving phase measurements. Phys. Rev. Lett. 98, 223601 (2007).
Humphreys, P. C. et al. Tomography of photon-number resolving continuous-output detectors. N. J. Phys. 17, 103044 (2015).
Pezzé, L., Smerzi, A., Khoury, G., Hodelin, J. F. & Bouwmeester, D. Phase detection at the quantum limit with multiphoton Mach-Zehnder interferometry. Phys. Rev. Lett. 99, 223602 (2007).
Daryanoosh, S., Slussarenko, S., Berry, D., Wiseman, H. & Pryde, G. Experimental optical phase measurement approaching the exact Heisenberg limit. Nat. Commun. 9, 2041–1723 (2018).
Vaidya, V. et al. Broadband quadrature-squeezed vacuum and nonclassical photon number correlations from a nanophotonic device. Sci. Adv. 6, eaba9186 (2020).
Flórez, J., Carlson, N. J., Nacke, C. H., Giner, L. & Lundeen, J. S. A variable partially polarizing beam splitter. Rev. Sci. Instrum. 89, 023108 (2018).
Figueroa-Feliciano, E. et al. Optimal filter analysis of energy-dependent pulse shapes and its application to TES detectors. Nucl. Instrum. Methods Phys. Res. 444, 453–456 (2000).
Acknowledgements
We thank B. Vlastakis for his assistance with the operation of the dilution refrigerator. This work was supported by the following: the Natural Sciences and Engineering Research Council of Canada (NSERC); the Networked Quantum Information Technologies Hub (NQIT) as part of the UK National Quantum Technologies Programme GrantEP/N509711/1) and within “First Team” project No. POIR.04.04.00-00-220E/16-00 (originally: FIRST TEAM/2016-2/17) of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund.
Author information
Authors and Affiliations
Contributions
Both G.S.T. and M.E.M. contributed equally. G.S.T. performed the experiment with assistance from B.A.B, C.G.W, A.E, D.S.P.; M.E.M., and G.S.T. performed numerical calculations with assistance from A.B.; A.E.L., T.G., and S.W.N. developed the detectors; R.B.P., M.S., A.I.L., and I.A.W. initiated and/or supervised the project; G.S.T. and M.E.M. wrote the paper with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thekkadath, G.S., Mycroft, M.E., Bell, B.A. et al. Quantum-enhanced interferometry with large heralded photon-number states. npj Quantum Inf 6, 89 (2020). https://doi.org/10.1038/s41534-020-00320-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00320-y
This article is cited by
-
Resolution of 100 photons and quantum generation of unbiased random numbers
Nature Photonics (2023)
-
Phase estimation of definite photon number states by using quantum circuits
Scientific Reports (2023)
-
On-chip beam rotators, adiabatic mode converters, and waveplates through low-loss waveguides with variable cross-sections
Light: Science & Applications (2022)
-
Quantum simulations with multiphoton Fock states
npj Quantum Information (2021)