Abstract
Traditionally, population genetics focuses on the dynamics of frequencies of alleles acquired by mutations on germ-lines, because only such mutations are heritable. Typical genotyping experiments, however, use DNA from some somatic tissues such as blood, which harbors somatic mutations at the current generation in addition to germ-line mutations accumulated since the most recent common ancestor of the sample. This common practice may sometimes cause erroneous interpretations of polymorphism data, unless we properly understand the role of somatic mutations in population genetics. We here introduce a very basic theoretical framework of population genetics with somatic mutations taken into account. It is easy to imagine that somatic mutations at the current generation simply add individual-specific variations, as errors in mutation detection do. Our theory quantifies this increment under various conditions. We find that the major contribution of somatic mutations plus errors is to very rare variants, particularly to singletons. The relative contribution is markedly large when mutations are deleterious. Because negative selection also increases rare variants, it is important to distinguish the roles of these mutually confounding factors when we interpret the data, even after correcting for demography. We apply this theory to human copy number variations (CNVs), for which the composite effect of somatic mutations and errors may not be negligible. Using genome-wide CNV data, we demonstrate how the joint action of the two factors, selection and somatic mutations plus errors, shapes the observed pattern of polymorphism.
Similar content being viewed by others
Introduction
Population genetics explicitly focuses on mutations in germ-line cells, because only such germ-line mutations can be inherited through generations and should be observed in polymorphism data. Strictly speaking, however, this logic does not hold unless the polymorphism data are directly obtained from zygotes that initiate the individuals’ development. In practice, it is quite common that surveys of genetic variation are carried out by using DNA extracted from somatic tissues such as blood, particularly for higher eukaryotes such as large animals and plants. In such a case, the polymorphism data should reflect both germ-line mutations accumulated since the most recent common ancestor and somatic mutations that occurred in the current generation. It has been believed that the relative contribution of the latter should be negligible, therefore no much attention has been paid to somatic mutations in population genetics. However, there seem to be cases where the effect of somatic mutations is not negligibly small. The purpose of this work is to theoretically explore the effect of somatic mutations on the pattern of polymorphism. We particularly focus on copy number variations (CNVs) as a case where the relative contribution of somatic mutations could be potentially large.
A great deal of attention has been paid to CNVs because of their potential impact on important phenotypes. It is now widely accepted that gene duplication is one of the major driving forces of genome evolution, because duplicated genes provide raw materials for genetic innovation (for example, Ohno, 1970 and Lynch, 2007). With the advent of sequencing and genotyping technologies, enormous amounts of data on CNVs have been generated and analyzed in various species (for example, Redon et al., 2006; Maydan et al., 2007; Emerson et al., 2008; Ossowski et al., 2008; Perry et al., 2008; She et al., 2008; Conrad et al., 2010; and Mills et al., 2011), and the evolutionary mechanisms behind the observed patterns of CNVs are getting extensively discussed from the view point of population genetics.
A potential problem in analyzing the CNV data using the standard population genetic theories could be a high rate of somatic mutations causing CNVs. It has been suggested that there are CNVs within a single individual, for example, between somatic cells from different tissues and between somatic and germ-line cells (for example, Piotrowski et al., 2008 and Mkrtchyan et al., 2010). Extensive copy number differences (CNDs) between monozygotic (MZ) twins can be another prominent example of such ‘somatic mosaicism’. By definition, MZ twins should share the same germ-line mutations inherited from their parents. Thus, aside from experimental errors, CNDs between MZ twins must have come solely from somatic mutations after twinning. Recently, pairs of MZ twins discordant for some phenotypes, especially disorders or diseases, have been frequently examined for genetic differences, including CNDs, to identify genetic causes of such phenotypes (for example, Bruder et al., 2008; Kimani et al., 2009; Baranzini et al., 2010; Maiti et al., 2010; Sasaki et al., 2011; and Ehli et al., 2012). The results of these studies varied widely in the number of CNDs identified, from zero (for example, Kimani et al., 2009 and Baranzini et al., 2010) to over a dozen per pair (Maiti et al., 2010). These results cannot be compared straightforwardly, because they were obtained through experiments that differ in their genomic coverage, resolution and/or criteria for validating detected CNV candidates. All we can say at this point is that there is currently no consensus on the rate of somatic CNV mutations; it could be negligibly small, or large enough to invalidate the use of traditional population genetics.
In such circumstances, it is all the more important to establish a theoretical framework of population genetics that takes somatic mutations into account, and to extensively examine the possible impacts of somatic mutations on the CNV data over a wide range of parameters. These are the main goals of this study. We will also demonstrate how our theoretical framework can be applied to real data, using the currently available data on human CNVs as examples. As the quality of data for somatic mutations still keeps improving, in the near future our theoretical framework will enable us to precisely evaluate the roles of evolutionary mechanisms behind the observed pattern of CNVs, including the exact contribution of somatic mutations to it.
The effects of somatic mutations are similar to those of errors in mutation detection. Numerous studies have addressed the issue of mutation detection errors, especially errors in single-nucleotide polymorphism (SNP) calls using DNA reads via shotgun sequencing or next-generation sequencing technologies (reviewed for example in Pool et al., 2010; Nielsen et al., 2011; Hohenlohe et al., 2012; and Liu, 2012). General theoretical frameworks of sequencing errors have been developed by many authors (for example, Johnson and Slatkin, 2006; Lynch 2009; Emerson et al., 2010; Hohenlohe et al., 2010; Liu et al., 2010; Martin et al., 2010; Keightley and Halligan, 2011; Kim et al., 2011; Li, 2011; Luca et al., 2011; and Nielsen et al., 2012), but they usually involve many parameters and are not easy to obtain analytical expressions. Some simplifications are needed to have informative analytical results, such as estimations of the population mutation rate θG, summary statistics and/or the derived allele frequency at each site (for example, Achaz, 2008; Hellmann et al., 2008; Johnson and Slatkin, 2008; Knudsen and Miyamoto, 2009; and Kofler et al., 2011). These theories may be useful for point somatic mutations, whose rate is somewhat comparable to that of germ-line mutations.
However, it is not straightforward to directly apply these theoretical frameworks to somtatic mutations that occurs at a relatively high rate, as may be the case with CNVs. Moreover, these theories somehow specialize in errors of SNPs by assuming either that the error rate is known exactly or that the forward and backward error rates are identical. These assumptions are not likely satisfied in current experiments to detect CNVs. Therefore, we here develop a new framework that incoporates both forward and backward somtatic mutations as well as both forward and backward detection errors. Our theory can also accommodate general population genetic models, which take account of demography, selection, and so on.
Results
Model
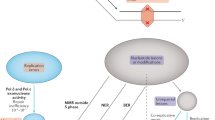
We consider a simple situation where n haploid genomes are sampled from a population with the current diploid population size Ncurr=N(0). We assume that the population size N(t) is given by a function of t, time measured backward from the present. We first focus on a single potentially variable locus (illustrated in Figure 1), then extend the result to a set of independent loci scattered across the genome. Two allelic states, wild type (W) and mutant (M), are allowed. Let uG and vG be the forward (from W to M) and backward (from M to W) germ-line mutation rates per generation per haploid, respectively (Figure 1, stage 1). Also, we assume that the DNA is sampled from a particular somatic tissue, such as a blood sample or a buccal swab, of each individual (Figure 2, stages 2–4). In such a situation, we expect that the sampled DNA accumulates a small number of detectable somatic mutations during cell cycles from the original zygote to the sampled tissue. Let uS and vS denote the rates of such detectable somatic mutations (per generation per haploid), forward and backward, respectively (Figure 1, from stage 2 to stage 3).
Three-step framework to predict the AFS taking account of somatic mutations. Consider a diploid population with size N(t) at time t (stage 1). Black and red bars represent wild-type and mutant alleles, respectively. Time t=0 is defined as the present (stage 2), and the standard population genetics can be applied to these zygotes at the current generation. Somatic mutations occur afterward (from stage 2 to stage 3), which, combined with errors in mutation detection, will be reflected in the observed state of the sample (stage 4). See text for details.
Schematic genealogy (a) and AFS (b) under a simple population genetic model with somatic mutations. A possible genealogy among haploid sequences is shown in (a). The stage numbers correspond to those in Figure 1. A large oval at stage 2 is a zygotic (haploid) genome. At stage 3, an open small oval and a red-shaded small oval are a somatic (haploid) genome and a germ-line one, respectively. A blue open box appended with a blue arrow (from stage 3 to stage 4) represents a sampled somatic tissue. (b) An expected AFS from these mutations is shown.
Errors in the detection of mutations have effects quite similar to those of somatic mutations (Figure 1, from stage 3 to stage 4). We assume that the average fraction uE of somatic DNA sequences with the true wild-type allele is erroneously identified as mutants (that is, false positives), and that the average fraction vE of true mutant somatic sequences are erroneously identified as wild types (that is, false negatives).
Selection can work at two levels. First, as the standard population genetics considers, selection works on germ-line mutations, which determines the number of offsprings in the next generation. For this selection, let 1, 1−hGsG and 1−sG be the relative fitnesses of individuals whose germ-line (or zygotic, to be more precise) genotypes are WW, WM and MM, respectively.
In addition, selection can work on somatic mutations. In general, a somatic mutation will not be passed on to descendants, but it potentially affects the non-inheritable fitness, that is, the survival probability and/or fertility that are relevant only to the individual having the somatic mutation. Throughout this study, we will ignore the fitness effects of somatic mutations, because the effects of somatic mutations on viability are expected to be negligibly small if only normal individuals are sampled. For example, in a population with the effective size Ne=10 000, even a somatic mutation whose fitness effect is equivalent to that of a severely deleterious germ-line mutation, say, 2NesG=200, can have 99% of wild-type viability. Thus, as the population genetic theory predicts, the effect of selection on a mutation is in general very limited (unless it is lethal or semi-lethal) at the individual level, even though the effect will be enhanced at the population level. This reasoning indicates that our assumption is not unreasonable especially when we are interested in detectable somatic mutations.
Basic theory
Under the above assumptions, we are interested in m, the number of haploids each with a CNV (that is, allele M) at the focal locus, out of n sampled haploids. We here derive the probability distribution of m, which will provide an allelic frequency spectrum later. The derivation involves three steps as illustrated in Figure 1:
(i) Predict the distribution φ(x) of the population frequency x of M among zygotes in the current generation (t=0, stage 2 in Figure 1), according to a standard population genetics theory, which takes account of germ-line mutations alone (Figure 1, stage 1).
(ii) Predict the frequency x′ of M among the somatic chromosomes to be sampled, conditional on x (Figure 1, stage 3). Then, predict the frequency x′′ of sequences that are observed to be of allele M in the experiment, by taking the effect of detection errors into account (Figure 1, stage 4).
(iii) Predict the probability distribution of m given n sampled somatic haploids, by averaging the binomial distribution of n trials with the success rate x′′ over the zygotic mutant frequency x (Figure 1, stage 4).
To predict the zygotic allele frequency distribution, φ(x), it is required to specify the past demographic history of the population, {N(t)}, the forward and backward germ-line mutation rates (uG and vG), and the selection parameters (sG and hG). We postpone this problem until later, and we first formulate steps (ii) and (iii) by assuming that φ(x|0)≡φ(x|t=0,{N(t)},uG,vG,sG,hG) in the current population (that is, at t=0 generation) is known. Henceforth, we will use a short-hand notation, 0≡(t=0,{N(t)},uG,vG,sG,hG), to represent this population genetic setting.
The step (ii) first concerns how somatic mutations change the allele frequency. Given the allele frequency x among zygotes and the rates of detectable somatic mutations, uS for forward and vS for backward, the population frequency of M at the sampling time is given by x′(uS,vS)=x(1−vS)+(1−x)uS, assuming no selection on somatic mutations. In addition, we incorporate the change in the frequency of sequences observed to be mutants. Let x′′ denotes the expected frequency of such ‘observed mutants’. Using the error rates uE and vE, it is given by:

Here, uSE and vSE are the ‘composite rates’ of somatic mutations and detection errors that give the net effect of forward (W to M) and backward (M to W) changes, respectively. They are defined as:


This approximation applies when uS, vS, uE, vE<<1, which holds in most practical cases. In simple experimental settings, we cannot distinguish somatic mutations and errors. Thus, frequency changes by somatic mutations and by detection errors are always combined together and measured through the composite rates uSE and vSE.
The step (iii) is straightforward; the probability that m out of n somatic haploids are observed to have allele M is given by the following basic formula:

Here, PBn[m|n,x′′] denotes a binomial probability, namely the probability of m ‘successes’ out of n trials when the success rate is x′′ per trial.
Figure 2 illustrates an intuitive expectation from this theoretical model. Inheritable germ-line mutations (red lightening bolts in stage 1 of panel a) are scattered across the genealogy, whereas detectable somatic mutations (blue lightening bolts from stage 2 to stage 3) occur only at the tip of the genealogy. Thus, each somatic mutation should affect a single haploid, most likely resulting in a unique mutant, that is, a singleton. Therefore, somatic mutations should contribute mostly to the singleton class in the allele frequency spectrum (AFS) (blue bar in panel b of Figure 2), whereas germ-line mutations are distributed into wider frequency classes (red bars). Because the n sampled haploids should be independently affected by somatic mutations, the absolute contribution of somatic mutations should amount roughly to nuS. These results are analogous to those on sequencing errors, such as their absolute contribution (∼nuE), which are derived, for example, by Achaz (2008), Hellmann et al. (2008) and Knudsen and Miyamoto (2009).
However, the behavior of backward mutation is not very simple. Below, we also explore the effect of backward mutations on the AFS under a relatively simplified situation, that is, the infinite site model is applied to germ-line mutations, but recurrent changes (including backward ones) are allowed after stage 2 (that is, somatic mutations and detection errors). The following results would enable more insightful mathematical understanding on the joint effects of forward and backward somatic mutations and errors.
AFS under the infinite site model
Equation (3) provides the basis of the following derivations. Obviously, without somatic mutations or errors, that is, with uSE=vSE=0, Equation (3) is identical to the well-known formula of the AFS, which only takes account of heritable germ-line mutations:

We refer to this AFS with no somatic mutation as the germ-line AFS.
It is often very convenient to expand Equation (3) with respect to the composite rates uSE and vSE, and express it in terms of the germ-line AFS:

with

If the composite rates are so small that nuSE<<1 and nvSE<<1, then the expansion could be approximated to the first order as:

This mathematical treatment is particularly powerful if the germ-line AFS is known either analytically or numerically. It also facilitates the comparison between (3) and (4), and helps evaluate the composite effect of somatic mutations and errors on the AFS. For this purpose, we here define Δ[m|0, uSE, vSE, n] as the relative difference between (3) and (4):

All computation through Equations (3, 4, 5, 6, 7) requires a germ-line allele frequency distribution, φ(x|0), which is determined by a specific set of population genetic parameters, 0, defined above. In general, numerical computation is possible for any kind of φ(x|0), and there are some special cases where the formula can be analytically given, either exactly or approximately. In the following, we will examine a few such cases assuming the infinite-site model (Kimura, 1969), where the germ-line mutation rates are so small that recurrent mutations are expected to be very rare. But we will allow recurrent changes from the zygotic state to the observed somatic state, via somatic mutations and/or detection errors. We also assume a constant-size population. In this section, we will use a short-hand notation,  , to represent the setting appropriate for the infinite-site models with a constant population size, N.
, to represent the setting appropriate for the infinite-site models with a constant population size, N.
It should be noted that in the following, we consider m={0, 1, 2, ..., n−1} and ignore the frequency class m=n. In practice, under the flux theory, once a derived allele is fixed, this fixed allele is regarded as a ‘new’ ancestral state. That is, the frequency class m=n is absorbed into the frequency class m=0 as soon as the mutant allele is fixed.
Selectively neutral mutations
When all mutations are selectively neutral, the equilibrium distribution φ*(x|...) of the mutant allele frequency x is given according to a flux theory (Kimura, 1969), which was later formulated using the Poisson random field theory (Sawyer and Hartl, 1992):

Substituting this for φ(x|0) in Equation (4), we get:

where  . Substituting this for P0[...] in Equation (6) and retaining up to the second leading terms, we get:
. Substituting this for P0[...] in Equation (6) and retaining up to the second leading terms, we get:

In terms of increments, this is translated as:

This predicts that, if we exclusively consider selectively neutral mutations, the expected increase in the frequency of singleton mutants will be  if uSE and uG are on the same order, and the increments of other frequency classes (m⩾2) are much smaller, given 4NuG<<1.
if uSE and uG are on the same order, and the increments of other frequency classes (m⩾2) are much smaller, given 4NuG<<1.
Deleterious mutations
Deleterious mutations may be common, especially when mutations occur in essential functional regions in the genome. To simplify the analysis, we assume that the fitness effects on germ-line mutants are additive, that is, hG=1/2. According to the Poisson random field theory (Sawyer and Hartl, 1992), the equilibrium distribution φ*(x|...) of the frequency x of a deleterious germ-line mutant is given as:

Substituting this for φ(x|...) in Equation (4), we get:

for m=1,...,n−1. Here,  is the confluent hypergeometric function. The probability P0[m=0|...] can be obtained from the general formula:
is the confluent hypergeometric function. The probability P0[m=0|...] can be obtained from the general formula:

Substituting Equation (13) into Equation (6), the increment of the spectrum of deleterious mutations is calculated, up to the first order of uSE and vSE, as:

for m=1,

for m=2,...,n−2, and

for m=n−1.
In the strong selection regime, 2NsG≫n, we can use the asymptotic expansion:

Up to the leading terms of the expansion, we have:

for m=1, ...,n−1. For m=0, we have

Substituting them for P0[...] in Equation (6) yields:

Equation (20) suggests that, if sG∼0.1 (and uG≈uSE), we will observe a roughly 5% increase in the singleton frequency. This simple approximation may roughly hold even with quite a large sG, say, up to ∼0.5.
Summary and implications
Figure 3 schematically summarizes the theoretical results we obtained above. There are a couple of very clear points. (1) First, whatever the germ-line AFS is, the major joint increment of the singleton frequency due to somatic mutations and errors is given by the forward composite rate, uSE, independent of germ-line mutation rates. In all cases (from neutral to very deleterious), the absolute contribution to the singleton class (that is, m=1) is nuSE, whereas those to the classes with m(>1) mutants are at most on the order of nuSE·P0[m−1|0,n] (see Supplementary Note 2 in Supplementary Information 1). Thus, the major contributions of somatic mutations and errors are to the singleton class, and the effect on other classes should be very small. (2) The relative contributions of somatic mutations and errors would be larger as selection is stronger against the mutant (M). This is obvious because the major absolute contributions of somatic mutations and errors are given by uSE alone while strong selection reduces the number of polymorphic loci substantially. Indeed, the proportion of singletons due to heritable mutations is θG (≡4NuG) when the mutation is selectively neutral (Figure 3a), roughly θGn/(2NsG) when it is strongly deleterious (Figure 3b and c), nuG when it is completely sterilizing (but not lethal at all), and 0 when it is lethal. (The latter two cases are discussed in Supplementary Note 1.)
Composite contributions of somatic mutations and errors to allele frequency spectra under various population genetic settings. It is assumed that all mutations are neutral (sG=0, a), moderately deleterious (2NsG=30, b) and strongly deleterious (2NsG=100, c). n=10, θG≡4NuG=0.001, vG=0, uSE=0.01θG, vSE=0 and hG=1/2 (that is, additive selection effect). The red bars represent the spectra due purely to germ-line mutations, and the blue bars represent the increments due to forward somatic mutations and false positives. Mathematical formulas for the contributions to the singleton class are shown on the right of two-headed arrows.
Although these conclusions were derived under the infinite-site model for mathematical convenience, they should also hold under finite-site models as long as the population mutation rate is sufficiently low that the majority of loci are monomorphic (see Supplementary Note 1). They should also hold even when the population size in the past is not constant because changes in the population size affect only the germ-line AFS but have no effect on the contributions of somatic mutations and errors.
These theoretical results caution against a naive evaluation of selection on CNVs using the AFS. It is known that both demography and selection affect the AFS. Accordingly, a common approach to evaluate selection on CNVs is to compare the spectrum of CNVs and that of SNPs at synonymous sites, which should be less affected by selection. It has been frequently demonstrated that the spectrum of CNVs is more skewed toward low frequencies than that of synonymous SNPs (for example, Emerson et al., 2008 and Conrad et al., 2010). Because selection provides one possible and popular interpretation of such a skew, the authors in the past large-scale analyses tended to conclude that CNVs are on average selected against. They further estimated selection parameters on CNVs from the allele frequency spectra, but so far without taking the effect of somatic mutations into account, although detection errors were somewhat corrected. We would point out that this approach could overestimate the effect of negative selection when the composite rate uSE is high enough to substantially increase the low-frequency classes of alleles, especially singletons. In the following, we will demonstrate this point by using an example of human CNVs, for which the somatic mutation rate may not necessarily be negligible. There, our theoretical framework will also reveal that the composite backward rate (vSE) can be disproportionally larger than the forward rate (uSE) in these experiments.
Application to human CNV data
The theoretical framework developed so far is readily applicable to real data. In the following, we will demonstrate it using two data sets on CNVs in humans as examples. One is a data set of CNDs between MZ twins (Maiti et al., 2010), which is used to estimate the composite rates of somatic mutations and mutation detection errors relative to the population-level diversity. With this estimate, we demonstrate how much the expected AFS could deviate from the prediction of traditional population genetics.
The other data set consists of three genome-wide allele frequency spectra of CNVs in the European population by Conrad et al. (2010), which are used for a maximum likelihood analysis to estimate the relative impacts of negative selection vs somatic mutations and errors on the allele frequency spectra, without prior information on the composite rates.
Estimating composite rates from CNDs between MZ twins
One potentially promising way to estimate the composite rates of somatic mutations and detection errors would be to exploit genetic differences between MZ twins, because such differences must have caused solely by somatic mutations or detection errors on either of the twins. While, as mentioned in Introduction, the rate of somatic CNV mutations is a controversial problem at this moment, we here use the data from Maiti et al. (2010). We use their data set because it is the only one we know that genotyped both twins and their parents, which allows us to distinguish forward and backward composite rates. In addition, because the twins’ (and their parents’) genomes are compared with a reference genome, we can also estimate the population germ-line mutation rate θG (≡4NeuG).
With the data of Maiti et al. (2010), we were able to estimate the forward composite rate relative to θG, as well as the absolute backward rate, as

as detailed in Supplementary Note 3 in Supplementary Information 1.
It should be noted that the study of Maiti et al. (2010) provides a virtual ‘upper-extreme’ of the extent of CNDs between twins among such studies conducted so far (see Introduction). Therefore, the potential impact of somatic mutations estimated in this subsection should be interpreted as an upper-bound.
By using an independent estimate of θG, we can compare the forward and backward composite rates, uSE and vSE. Using the data of Conrad et al. (2010), we estimated the genome-wide proportion of segregating CNV loci as 0.024 (see Supplementary Note 4 for detail). Because this is based on the data of sample size 40, we can roughly estimate θG as 0.024/(1+1/2+···+1/39)∼5.6 × 10−3 according to Watterson (1975). Thus, we have a broad estimate of uSE as 0.097 × 5.6 × 10−3∼5.4 × 10−4, which is only ∼1/250 of vSE (∼0.13). One possible explanation of this large discrepancy is that at least vSE (and perhaps also uSE) may be mostly due to errors in the array experiments of Maiti et al. (2010). This estimate of the backward composite rate seems to be too large if somatic mutations are its major source; vSE≈0.13 is even higher than the exceptionally high mutation rates (∼10−4) that some disease-associated structural variants are known to have (see for example Lupski, 2007). High error rates of array experiments have also been pointed out, for example, by Emerson et al. (2008).
It would be intriguing to demonstrate how the estimated total amount of somatic mutations and errors can potentially affect the AFS. To be realistic, we first construct a presumable spectrum for selectively neutral germ-line CNVs among 40 European haploids via the Poisson Random Field theory (for example, Sawyer and Hartl, 1992 and Williamson et al., 2005) implemented in the ‘prfreq’ program (Boyko et al., 2008). The demography of the population was modeled by the ‘bottleneck+2-step recovery’ model with the parameters provided in Table S1 of Boyko et al. (2008). The demographic parameters were inferred by Boyko et al. (2008) using ca. 8700 synonymous SNPs among 20 European-Americans. The obtained spectrum is shown by red bars in Figure 4.
Onto this spectrum, we added the composite effect of CNV somatic mutations and errors (as estimated above) according to the full expansion formula in Equation 5. The result is shown by blue bars in Figure 4. It demonstrates that there could be a substantial increase in the singleton class, while there are very little contributions to the other frequency classes. This result indicates that the composite effect of somatic CNV mutations and errors on population genetic analysis may not be negligible, provided that the forward composite rate in the spectrum analysis is indeed as high as that estimated from the data of Maiti et al. (2010). Thus, as mentioned earlier, neglecting somatic mutations and errors could potentially make us to misinterpret a substantial excess of singletons as evidence for selection against CNVs.
It is important to point out that there is a major difference in how the two factors (selection and somatic mutations plus errors) affect the AFS, although both cause skews toward rare frequency classes. As our theory shows, somatic mutations and errors affect primarily the singleton class, whereas the effect of selection can be observed in all frequency classes. Based on this difference, in the next section, we attempt to distinguish these two mutually confounding factors using the spectrum data alone.
Selection vs somatic mutations plus errors inferred from the AFS
In the previous section, we estimated the composite rates of CNV somatic mutations and errors, which enabled us to understand their impact on the AFS. Thus, when we have some prior information on the composite rates (for example, by twins data), it is straightforward to predict its effect on population genetic analysis. However, composite rates predicted from one experiment may not apply to other experiments particularly because of potentially large heterogeneity in error rates. Moreover, for many non-model species, such prior estimates of composite rates may not be available at all. In such situations, it would be more powerful if we can distinguish between the composite effect of somatic mutations and errors and the effect of selection using the spectrum data alone.
We here use a likelihood approach to estimate the composite rates and selection parameters simultaneously from the AFS. (The computational procedures are detailed in Supplementary Note 4.) It is assumed that the expected spectrum of neutral germ-line mutations (with no somatic mutation) is known but that the composite rates are unknown. We obtain such a presumably ‘neutral’ spectrum under the demographic model inferred from synonymous SNPs by the ‘prfreq’ program (Boyko et al., 2008), as already described in the previous subsection.
As an observed frequency spectrum, we use the exonic CNV data with n=40 haploids of an European origin, which were kindly provided by Conrad et al. (2010) (see also Figure 2.28 in their Supplementary Notes). The white bars in Figure 5a show this observed spectrum, which is denoted by  , where
, where  (k=1,..., B) is the observed number of CNV loci in the kth bin consisting of one or more of the allele frequency classes, each of which is defined by a particular number of mutants in the sample. Here, we define B=16 bins out of n−1=39 allele frequency classes, as indicated by the labels under the horizontal line in Figure 5. Such a practice is quite common in χ2 goodness-of-fit tests in which some allele frequency classes have very few (or zero) entries, as in the present case. We first check how a neutral model (demography taken into account) with no effects of selection, somatic mutations, or errors can explain the observed frequency spectrum by using a likelihood approach. A log-likelihood function of the observed spectrum is given by
(k=1,..., B) is the observed number of CNV loci in the kth bin consisting of one or more of the allele frequency classes, each of which is defined by a particular number of mutants in the sample. Here, we define B=16 bins out of n−1=39 allele frequency classes, as indicated by the labels under the horizontal line in Figure 5. Such a practice is quite common in χ2 goodness-of-fit tests in which some allele frequency classes have very few (or zero) entries, as in the present case. We first check how a neutral model (demography taken into account) with no effects of selection, somatic mutations, or errors can explain the observed frequency spectrum by using a likelihood approach. A log-likelihood function of the observed spectrum is given by
Model fitting to the AFS data of exonic CNVs (a) and intergenic CNVs (b) in humans. The observed spectrum is shown by the white bars. The colored bars show the best-fit spectra under the four models. The color code is red, the model with neutral germ-line mutation only; green, the model with selection; blue, the model with somatic mutations (plus errors); orange, the model with both selection and somatic mutations (plus errors). Demography is taken into account in all four models (see text for details).

Here,  (k=1,...,B) is the theoretical expectation of the proportion of the kth bin, which is normalized so that
(k=1,...,B) is the theoretical expectation of the proportion of the kth bin, which is normalized so that  .
.  is computed from Equation (3) by assuming that the CNV regions are unlinked to each other and that all loci have identical mutation rates and selection parameters.
is computed from Equation (3) by assuming that the CNV regions are unlinked to each other and that all loci have identical mutation rates and selection parameters.
In the neutral model with the demography estimated from synonymous SNPs, it is straightforward to calculate the expected spectrum with no somatic mutation or error (red bars in Figure 5a). The fit is not very good, as the theoretical spectrum has much fewer singletons and much more loci with k⩾2 than the observation. The poor fit is also indicated by an extremely small goodness-of-fit P-value (=5.9 × 10−50). The result therefore suggests potential roles of selection and/or the composite effect of somatic mutations and errors.
Next, we include selection in the theoretical model. It somewhat improves the fit to the observation, but the spectrum with the maximum likelihood still deviates from the observation in the same directions as the purely germ-line neutral spectrum does (green bars in Figure 5a), and the goodness-of-fit P-value remains quite small (=1.3 × 10−19), although significantly improved in comparison with the basic neutral model with P=5.9 × 10−50. Note that a larger P-value (or, equivalently, a smaller χ2) indicates a better fit. The improvement is highly significant (P=5.4 × 10−35, likelihood ratio test).
In contrast, when the composite effect of somatic mutations and errors is added to the neutral germ-line CNV model, the fit to the observation is dramatically improved. The theoretical spectrum with the maximum likelihood is almost indistinguishable from the observation (blue bars in Figure 5a), and the goodness-of-fit P-value (=1.6 × 10−6) becomes much larger (P=2.0 × 10−49, likelihood ratio test).
Finally, we add both selection and the composite effect of somatic mutations and errors to the purely germ-line neutral model. This case fits the observation best (the goodness-of-fit P-value=5.3 × 10−5 and P=1.1 × 10−50 for a likelihood ratio test) as shown by orange bars in Figure 5a, although the neutral CNV model with somatic mutations and errors explains the data almost equally well. A synopsis of these results, including the maximum-likelihood (ML) estimates of parameters, are given as Table S1 in Supplementary Information 2.
The same analyses are also applied to the data for intergenic CNVs and intronic CNVs from the identical sample of 20 Europeans (Conrad et al., 2010). We again found that the model incorporating both selection and somatic mutations plus errors best explains the observations (Table S1, Figure 5b and Supplementary Figure S11 in Supplementary Information 2). However, in contrast with the exonic data, incorporating selection alone fitted intronic and intergenic data better than incorporating only somatic mutations and errors did. This might be against intuition, but can be explained by our theory. If selection works against CNVs (as in the exonic case), then the relative contributions of somatic mutations and errors to rare allele frequencies are large. In such cases, their effect should stand out in our ML analysis.
Through this model-fitting approach by maximizing the log-likelihood function, Equation (22), there are two major points to make. First, the inclusion of somatic mutations plus errors drastically reduced the magnitude of the estimates of selection coefficient γ (≡−NcurrsG) for exonic CNVs, from γMLE=−24.3 for the purely germ-line model with selection to γMLE=−9.2 for the model with both selection and somatic mutations plus errors. Indeed, the former model is nested in the latter, and the likelihood ratio test (of 2 degrees of freedom) favors the latter with a P-value of 1.1 × 10−18. The coefficient γ reduced also for intronic and intergenic CNVs although the reduction was not so significant. Thus, ignoring somatic mutations likely causes an overestimation of the role of negative selection in the analysis of the AFS.
Second, the maximum likelihood estimates (MLEs) of the forward composite rate were in general much smaller than the rates estimated using the CNDs between twins in the previous section, whereas the estimates of backward composite rate vSE were roughly in agreement. The MLE of the ratio uSE/θG for the full model (with both selection and somatic mutations plus errors) was 0.079, 0.0071 and 0.0042 for exonic, intronic and intergenic CNVs, respectively. Thus, except for the exonic CNVs, the ratio was much smaller than the estimate of 0.097 via the analysis of CNDs between twins. This may be because: (1) most of the data of Conrad et al. (2010) are deletions whereas the majority of CNDs between twins identified by Maiti et al. (2010) are duplications; (2) the CNDs collected by Maiti et al. (2010) are somewhat biased toward deleterious ones (maybe due to coding regions of genes with potential association with diseases, much larger CNV sizes compared with those in Conrad et al., 2010, and so on); and/or (3) the array-based experimental data by Maiti et al. (2010) may contain a higher proportion of false positives than that by Conrad et al. (2010).
It is straightforward to understand the difference in uSE/θG between exonic and non-exonic regions. Exonic CNVs are much more likely very deleterious and eliminated from the population quickly, so that they do not contribute much to the germ-line allele frequency distribution. This effectively reduces the rate uG of observable germ-line CNVs, and thus ends up in the reduction of θG (≡4NeuG). In contrast, the effect of selection against somatic mutations should be negligible and that against errors should be none, so that such an effective reduction in the mutation rate is not expected for uSE. Combined together, these two contrasting effects result in a large uSE/θG ratio for exonic CNVs.
Throughout our ML analyses, we used a particular demographic model, that is, the ‘bottleneck+2 step recovery’ model by Boyko et al. (2008). To examine the possible effects of this choice of the demographic model, we repeated our analyses using their second best-fit model, namely the ‘bottleneck’ model by Boyko et al. (2008), and confirmed that the conclusions remain unchanged even under the latter demographic model (data not shown).
Discussion
Traditional population genetic theories deal exclusively with mutations accumulated through generations of germ-lines down to zygotes of the current generation, whereas in experiments genotypes are commonly determined from somatic cells. Whether such a common practice causes any problem or not depends crucially on how much somatic mutations can impact population genetic data. To the best of our knowledge, this study is the first to theoretically formulate and systematically quantify such effects of somatic mutations in population genetics. The impact of somatic mutations on polymorphism data is straightforward; it adds extra mutations that occurred at the current generation. Such mutations should be individual specific, so that most of them should be observed as singletons or very rare variants. In this sense, the effects of somatic mutations are almost indistinguishable from those of errors in mutation detection. The composite effect of these two factors is clearly quantified by our theoretical framework. As our theory (see also Figure 3) demonstrates, the major contributions of somatic mutations and errors are to the singleton class, and their contributions to other frequency classes are very small.
This effect is similar to that of negative selection, one of the major factors to increase rare variants. A major difference is that somatic mutations and errors result almost solely in singletons, while negative selection leaves other rare variant classes as well, particularly when the selection is weak or moderate. This is because negative selection decreases the absolute level of polymorphism; the reduction is remarkable especially for common variants. As a side effect of this more reduced polymorphism by stronger negative selection, the relative composite contribution of somatic mutations and errors becomes larger as shown in Figure 3. This holds regardless of how the germ-line AFS is shaped by the joint action of demography and selection.
In this work, we demonstrated practical aspects of our theory by applying it to human CNV data as examples. We estimated quite high composite rates of somatic mutations and detection errors, uSE and vSE, from the data of Maiti et al. (2010), which suggested the potential importance of considering their effects on population genetic analyses. A notable example should be analyses based on the allele frequency spectra, from which the role of selection is commonly argued. We introduced an ML approach to distinguish between their effects using the allele frequency spectra, and found both have significant roles to increase rare CNVs in human. It should be noted that several authors suggested conventional analyses while excluding singletons, because sequencing errors impact the singleton class most remarkably (for example, Achaz, 2008; Hellmann et al., 2008; and Knudsen and Miyamoto, 2009). Although reasonable for SNP data, this simple method may not fully exclude the composite effect of somatic mutations and errors on CNV data, because the composite backward rate vSE of CNVs may be quite large as we estimated in this article.
A limitation of the selection model we used is that it assumes a constant selective pressure for all CNVs. There should be a substantial variation in selection intensity especially on exonic CNVs; some must be very deleterious while others may be close to neutral. In such a situation, the expected spectrum should be a mixture of spectra that are highly skewed toward rare variants and near neutral spectra. Indeed, a large fraction of exonic CNVs in the data of Conrad et al. (2010) should be very deleterious given that a majority of their CNVs are deletions, which should have stronger impacts on phenotypes than duplications do. Therefore, a model with both highly deleterious germ-line mutations and almost neutral ones would also fit the AFS of human exonic CNVs almost as well as our models with somatic mutations do. To confirm this idea, we used a germ-line mutation model where a proportion (pneu) of loci are selectively neutral and the remaining ones share a single selection coefficient (γ), and we fitted the model to the observed AFS of exonic CNVs under the ML criterion. The MLEs of the parameters were pneu=0.092 and γ=−438, and the goodness-of-fit test gave χ2=49.7 and P=3.4 × 10−6, which are only slightly better than the values for the neutral model with somatic mutations plus errors (Supplementary Table S1). It is indicated that more sophisticated models would be helpful to fully understand the joint roles of selection and somatic mutations plus errors, especially when more data become available.
In our theoretical framework, it is very difficult to distinguish the effect of somatic mutations and that of mutation detection errors. Discrimination between these two factors may be possible experimentally. If the detection errors occur randomly, then they may be identified by repeating the genotyping experiments many times on the same locus from the same sampled tissue. In the multiple rounds of experiments, somatic mutations (as well as heritable mutations) will be detected consistently but errors will be detected at most only a few times, thus errors could be filtered out. In any case, improved knowledge of the rates of somatic mutations and detection errors will enhance our understanding on the mechanisms to maintain CNVs in a population.
Although we used the CNV data for humans, our theoretical framework can be applied to any species as long as sampled DNA accumulates detectable somatic mutations. Exceptions include small organisms such as Drosophila, whose DNA is typically extracted from the entire body rather than a certain tissue. In such a case, the effect of somatic mutations on polymorphism data is minimized, because a mutation on a certain somatic lineage would be diluted by other body parts lacking the mutation, weakening the signal to an undetectable level. This prediction is consistent with Emerson et al. (2008), who reported a relatively small estimate of selection coefficient against CNVs in Drosophila. This may be partly because the selection intensity was not overestimated so greatly due to the less effect of somatic mutations. Another implication of our theory is that the small estimate may be due to the population size of Drosophila, which is much larger than that of humans. Because the total contribution of somatic mutations and errors is ca. nuSE and that of germ-line mutations is somewhat proportional to θG≡4NeuG (see Figure 3 and the summary of our theoretical results), the relative contribution of somatic mutations is small if the population size is large. Thus, neither somatic mutations nor detection errors would cause a serious overestimation of the selection coefficient on fly CNVs.
Data archiving
There were no data to deposit.
References
Achaz G . (2008). Testing for neutrality in samples with sequencing errors. Genetics 179: 1409–1424.
Baranzini S, Mudge J, van Velkinburgh J, Khankhanian P, Khrebtukova I, Miller N et al. (2010). Genome, epigenome and RNA sequences of monozygotic twins discordant for multiple sclerosis. Nature 464: 1351–1356.
Boyko A, Williamson S, Indap A, Degenhardt J, Hernandez R, Lohmueller K et al. (2008). Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet 4: e1000083.
Bruder C, Piotrowski A, Gijsbers A, Andersson R, Erickson S, de Stahl T et al. (2008). Phenotypically concordant and discordant monozygotic twins display different DNA copy-number-variation profiles. Am J Hum Genet 82: 763–771.
Conrad D, Pinto D, Redon R, Feuk L, Gokcumen O, Zhang Y et al. (2010). Origins and functional impact of copy number variation in the human genome. Nature 464: 704–712.
Ehli E, Abdellaoui A, Hu Y, Hottenga J, Kattenberg M, van Beijsterveldt T et al. (2012). De novo and inherited CNVs in MZ twin pairs selected for discordance and concordance on attention problems. Eur J Hum Genet 20: 1037–1043.
Emerson J, Cardoso-Moreira M, Borevitz J, Long M . (2008). Natural selection shapes genome-wide patterns of copy-number polymorphism in Drosophila melanogaster. Science 320: 1629–1631.
Emerson K, Merz C, Catchen J, Hohenlohe P, Cresko W, Bradshaw W et al. (2010). Resolving postglacial phylo-geography using high-throughput sequencing. Proc Natl Acad Sci USA 107: 16196–16200.
Hellmann I, Mang Y, Gu Z, Li P, de la Vega F, Clark A et al. (2008). Population genetic analysis of shotgun assemblies of genomic sequences from multiple individuals. Genome Res 18: 1020–1029.
Hohenlohe P, Bassham S, Etter P, Stiffler N, Johnson E, Cresko W . (2010). Population genomics of parallel adaptation in threespine stickleback using sequenced RAD tags. PLoS Genet 6: e1000862.
Hohenlohe P, Catchen J, Cresko W . (2012). Population genomic analysis of model and nonmodel organisms using sequenced RAD tags. Methods Mol Biol 888: 235–260.
Johnson P, Slatkin M . (2006). Inference of population genetic parameters in metagenomics: a clean look at messy data. Genome Res 16: 1320–1327.
Johnson P, Slatkin M . (2008). Accounting for bias from sequencing error in population genetic estimates. Mol Biol Evol 25: 199–206.
Keightley P, Halligan D . (2011). Inference of site frequency spectra from high-throughput sequence data: quantification of selection on nonsynonymous and synonymous sites in humans. Genetics 188: 931–940.
Kim S, Lohmueller K, Albrechtsen A, Li Y, Korneliussen T, Tian G et al. (2011). Estimation of allele frequency and association mapping using next-generation sequencing data. BMC Bioinformatics 12: 231.
Kimani J, Yoshiura K, Shi M, Jugessur A, Moretti-Ferreira D, Christensen K et al. (2009). Search for genomic alterations in monozygotic twins discordant for cleft lip and/or palate. Twin Res Hum Genet 12: 462–468.
Kimura M . (1969). The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 61: 893–903.
Knudsen B, Miyamoto M . (2009). Accurate and fast methods to estimate the population mutation rate from error prone sequences. BMC Bioinformatics 10: 247.
Kofler R, Orozco-terWengel P, De Maio N, Pandey R, Nolte V, Futschik A et al. (2011). PoPoolation: a toolbox for population genetic analysis of next generation sequencing data from pooled individuals. PLoS One 6: e15925.
Li H . (2011). A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics 27: 2987–2993.
Liu X . (2012). jPopGen Suite: population genetic analysis of DNA polymorphism from nucleotide sequences with errors. Methods Ecol Evol 3: 624–627.
Liu X, Fu Y, Maxwell T, Boerwinkle E . (2010). Estimating population genetic parameters and comparing model goodness-of-fit using DNA sequences with error. Genome Res 20: 101–109.
Luca F, Hudson R, Witonsky D, Di Rienzo A . (2011). A reduced representation approach to population genetic analyses and applications to human evolution. Genome Res 21: 1087–1098.
Lupski J . (2007). Genomic rearrangements and sporadic disease. Nat Genet 39: S43–S47.
Lynch M . (2007) The Origin of Genome Architecture. Sinauer Associates: Sunderland, MA.
Lynch M . (2009). Estimation of allele frequencies from high-coverage genome-sequencing projects. Genetics 182: 295–301.
Maiti S, Kumar K, Castellani C, O'Reilly R, Singh S . (2010). Ontogenetic in de novo copy number variations (CNVs) as a source of genetic individuality: Studies on two families with MZD twins for schizophrenia. PLoS One 6: e17125.
Martin E, Kinnamon D, Schmidt M, Powell E, Zuchner S, Morris R . (2010). SeqEM: an adaptive genotype-calling approach for next-generation sequencing studies. Bioinformatics 26: 2803–2810.
Maydan J, Lorch A, Edgley M, Flibotte S, Moerman D . (2007). Copy number variation in the genomes of twelve natural isolates of Caenorhabditis elegans. Nat Genet 39: S43–S47.
Mills R, Walter K, Stewart C, Handsaker R, Chen K, Alkan C et al. (2011). Mapping copy number variation by population-scale genome sequencing. Nature 470: 59–65.
Mkrtchyan H, Gross M, Hinreiner S, Polytiko A, Man-velyan M, Mrasek K et al. (2010). The human genome puzzle—the role of copy number variation in somatic mosaicism. Curr Genomics 11: 426–431.
Nielsen R, Korneliussen T, Alberchtsen A, Li Y, Wang J . (2012). SNP calling, genotype calling, and sample allele frequency estimation from new-generation sequencing data. PLoS One 7: e37558.
Nielsen R, Paul J, Albrechtsen A, Song Y . (2011). Genotype and SNP calling from new-generation sequencing data. Nat Rev Genet 12: 443–451.
Ohno S . (1970) Evolution by Gene Duplication. Springer: Heidelberg, Germany.
Ossowski S, Schneeberger K, Clark R, Lanz C, Warth-mann N, Weigel D . (2008). Sequencing of natural strains of Arabidopsis thaliana with short reads. Genome Res 18: 2024–2033.
Perry G, Yang F, Marques-Bonet T, Murphy C, Fitzgerald T, Lee A et al. (2008). Copy number variation and evolution in humans and chimpanzees. Genome Res 18: 1698–1710.
Piotrowski A, Bruder C, Andersson R, de Stahl T, Menzel U, Sandgen J et al. (2008). Somatic mosaicism for copy number vari.aon in differentiated human tissues. Hum Mutat 29: 1118–1124.
Pool J, Hellmann I, Jensen J, Nielsen R . (2010). Population genetic inference from genomic sequence variation. Genome Res 20: 291–300.
Redon R, Ishikawa S, Fitch K, Feuk L, Perry G, Andrews T et al. (2006). Global variation in copy number in the human genome. Nature 444: 444–454.
Sasaki H, Emi M, Iijima H, Ito N, Sato H, Yabe I et al. (2011). Copy number loss of (src homology 2 domain containing)-transforming protein 2 (SHC2) gene: discordant loss in monozygotic twins and frequent loss in patients with multiple system atrophy. Mol Brain 4: 24.
Sawyer S, Hartl D . (1992). Population genetics of polymorphism and divergence. Genetics 132: 1161–1176.
She X, Cheng Z, Zöllner S, Church D, Eichler E . (2008). Mouse segmental duplication and copy number variation. Nat Genet 40: 909–914.
Watterson G . (1975). On the number of segregating sites in genetical models without recombination. Theor Popul Biol 7: 256–276.
Williamson S, Hernandez R, Fledel-Alon A, Zhu L, Nielsen R, Bustamante C . (2005). Simultaneous inference of selection and population growth from patterns of variation in the human genome. Proc Natl Acad Sci USA 102: 7882–7887.
Acknowledgements
We are grateful to Adam Boyko at Cornell University for kindly providing us with the program ‘prfreq’ and giving instructions on how to use it. We thank Donald F Conrad at Washington University and Matthew E Hurles at the Wellcome Trust Sanger Institute for kindly providing us with the original numerical data of their CNV allele frequency spectra. We also appreciate the comments and suggestions of the editor and three referees, who helped improve our manuscript. This work was supported by a grant from Japan Science and Technology Agency (JST) to HI.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on Heredity website
Supplementary information
Rights and permissions
About this article
Cite this article
Ezawa, K., Innan, H. Theoretical framework of population genetics with somatic mutations taken into account: application to copy number variations in humans. Heredity 111, 364–374 (2013). https://doi.org/10.1038/hdy.2013.59
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2013.59