Abstract
It is well known that tsunamis can produce gravity waves that propagate up to the ionosphere generating disturbed electron densities in the E and F regions. These ionospheric disturbances can be studied in detail using ionospheric total electron content (TEC) measurements collected by continuously operating ground-based receivers from the Global Navigation Satellite Systems (GNSS). Here, we present results using a new approach, named VARION (Variometric Approach for Real-Time Ionosphere Observation), and estimate slant TEC (sTEC) variations in a real-time scenario. Using the VARION algorithm we compute TEC variations at 56 GPS receivers in Hawaii as induced by the 2012 Haida Gwaii tsunami event. We observe TEC perturbations with amplitudes of up to 0.25 TEC units and traveling ionospheric perturbations (TIDs) moving away from the earthquake epicenter at an approximate speed of 316 m/s. We perform a wavelet analysis to analyze localized variations of power in the TEC time series and we find perturbation periods consistent with a tsunami typical deep ocean period. Finally, we present comparisons with the real-time tsunami MOST (Method of Splitting Tsunami) model produced by the NOAA Center for Tsunami Research and we observe variations in TEC that correlate in time and space with the tsunami waves.
Similar content being viewed by others
Introduction
The notion that gravity waves generated by tsunami waves (even with wave heights of a few centimeters in deep ocean) can propagate upward in the atmosphere and ultimately cause perturbations in the total electron content (TEC) of the ionosphere was first established by Daniels1, and was theoretically further developed by Hines2,3. Peltier and Hines4 subsequently showed that these TEC variations can be detected through ionosonde measurements.
Using this solid foundation and the abundance of GPS observations, researchers have set out goals to develop models and establish observational systems to provide reliable tsunami forecasts before the actual tsunami waves reach coastlines. It has been demonstrated that effects of an ocean tsunami can potentially be remotely observed as traveling ionospheric disturbances (TIDs) produced by the gravity waves. These TIDs were detected using different methods of observation, including ground-GPS5,6,7, Jason-1 radar altimeter8,9, incoherent scatter radar (ISR) at Arecibo10 and space-based measurements11,12.
Additional investigations highlighted that the detection of tsunami-driven TIDs is not always straightforward since there exists several other causes for TIDs, such as intense or large-scale tropospheric weather13,14,15, geomagnetic and auroral activity16,17, earthquakes18,19,20, and even unknown mechanisms21. Therefore, the relationship between detected TIDs and those that are induced by a tsunami has to be proven, for example by verifying that the horizontal speed, direction and spectral bandwidth of the TIDs match that of the ocean tsunami7.
While there has been progress in experimental work, along with theoretical modeling of the interactions between the ocean surface, atmosphere, and ionosphere8,22,23,24,25, recent reviews presented by26,27 concluded that the core scientific problems regarding the nature of the coupling between the ocean and ionosphere are still not sufficiently understood. To provide actionable geophysical data on the inferred amplitude, period, and velocity of a tsunami, based on the estimated gravity wave-induced TIDs, a number of real-time TEC monitoring systems are being developed utilizing the present capabilities of GNSS technology and infrastructures. As a matter of fact, up to now TEC variations are routinely estimated and geolocated in a post-processing mode.
The existing tsunami warning systems currently rely on numerical modeling (as MOST) and buoy observations7. Since the 2003 Rat Islands tsunami, the NOAA Center for Tsunami Research (NCTR) has developed a real-time model-forecast methodology ingesting deep-ocean tsunami measurements into the MOST model to produce timely and accurate tsunami forecasts for potentially vulnerable U.S. coastal communities28,29,30,31,32. As a major model component of this forecast system, MOST has been used to develop a database of tsunami propagation model results for nearly 2,000 tsunami sources covering all known subducting zones on earth. Based on an inversion algorithm33, the forecast method rapidly estimates the tsunami source to obtain a best fit between the pre-computed tsunami propagation database and the real-time tsunami measurements supported by a global tsunameter system composed of 65 deep-ocean bottom pressure sensors. Ground-GNSS observations processed in real-time may have the potential to enhance the current system by independently providing the tsunami speed and amplitude.
We are presenting a new GNSS processing algorithm, named VARION (Variometric Approach for Real-Time Ionosphere Observation) that focuses on the real-time detection of the TIDs caused by tsunami atmospheric gravity waves (see Appendix A for the methodology). VARION is an open source, entirely Python-based software (https://github.com/giorgiosavastano/VARION). It was derived from the VADASE (Variometric Approach for Displacements Analysis Standalone Engine) algorithm that was successfully applied to estimate in a real-time scenario the ground velocities and displacements induced by several earthquakes (e.g. the Tohoku-Oki earthquake, USGS Mw 9.0, 11 March 2011, 05:46:24 UTC; the Emilia earthquake, USGS Mw 6.0, 20 May 2012, 02:03:52), using a stand-alone GNSS receiver34,35,36. The VADASE algorithm was later modified and applied to geometry-free combinations of GNSS carrier-phase measurements for estimating TEC variations. Using the VARION algorithm each dual-frequency GNSS receiver is expected to provide time series of real-time TEC variations in a stand-alone operational mode.
For the validation of the algorithm we consider ionosphere effects of the tsunami generated by the Magnitude 7.8 - Haida Gwaii earthquake, that occurred at 03:04:08 Universal Time (UT) on 28 October 2012, 207 km SW of Prince Rupert, Canada (USGS, 2012). We investigate gravity waves observed in the ionosphere in the Island of Hawaii more than 4000 km from the epicenter and reached by the tsunami about 5 hours later. The NCTR’s real-time estimate of the tsunami source was based on an inversion process to fit the pre-computed model database with the tsunami records from the closest tsunameter 46419. The tsunami source was estimated to have a rupture area of 200 × 50 km2 with an average slip of 3.6 m, giving an earthquake moment magnitude of 8.0. Based on this source estimation, the model results were rapidly assembled to provide a basin-wide model forecast of tsunami propagation, including the waves propagating through the Hawaiian Islands used for comparison with the sTEC perturbations in the present study.
The Datasets section introduces the data and methodology used in the investigation and the results are presented and discussed in the section Results and Discussion. In the Conclusion section we present our conclusions and additional details about the VARION approach are offered in Appendix A.
Datasets
GPS dataset
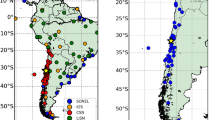
To estimate the TEC variations we used the GPS observations collected at 56 Plate Boundary Observatory (PBO) sites located on the Hawaiian Islands (https://www.unavco.org/instrumentation/networks/status/pbo). All the GPS permanent stations are located on the Big Island (Hawai’i), (see Fig. 1). Observations were acquired at 15- and 30-seconds cadence.
The map has been generated using the matplotlib Basemap toolkit55.
GPS processing
To process GPS observations we used two independent software packages. The VARION package based on single time differences of geometry-free combinations of GPS carrier-phase measurements, using a standalone GPS receiver and standard GPS broadcast products (orbits and clock corrections) that are available in real-time; and the bias-fixing Jet Propulsion Laboratory (JPL) technique that returns the absolute TEC values37, using a network approach to estimate the satellite and receiver interfrequency biases using the Global Ionospheric Mapping (GIM) software38.
Tsunami model
For verifying the agreement of the estimated TEC variations with the tsunami, we used the real-time MOST (Method of Splitting Tsunami) model provided by the NOAA research center. The model employs a finite-difference approximation of the characteristic form of the shallow water wave equations by use of the splitting method39,40. For propagation, MOST uses the shallow water equations in spherical coordinates with numerical dispersion to account for different propagation wave speeds at different frequencies41. MOST uses the elastic model of Okada42 to compute the initial seafloor deformation resulting from a source model, which is then used directly as the initial deformation of the ocean surface in the model43.
Results and Discussion
We processed the GPS observations from the 56 PBO GPS stations to estimate TEC variations at 15 s and 30 s rate with both VARION and JPL algorithms37. These two algorithms are designed to directly estimate two different parameters. As mentioned, the JPL algorithm is able to directly obtain the absolute TEC values, after estimating highly precise satellite and receiver Inter-Frequency Biases (IFBs) using about 200 GPS receivers distributed worldwide [e.g., refs 38, 44]. On the other hand, the direct outputs of the VARION algorithm are the sTEC variations (Equation 3), subsequently integrated over a certain time period; the variometric approach overcomes the problem of estimating the phase initial ambiguity and the IFBs, thus being ideal for real-time applications.
In order to highlight the TIDs, the TEC time series for each satellite were filtered to remove the TEC low-frequency variations (such as diurnal variations and multiple hour trends due to changing satellites elevation angles); VARION results were filtered using an 8th order polynomial, while the JPL algorithm uses a band-pass filter (0.5 to 5 mHz)45.
Figure 2 shows the sTEC time series for two hours (08:00 to 10:00 UT - 28 October 2012) for 7 satellites in view from the AHUP station obtained with the two approaches. The vertical black line represents the time when the tsunami arrived at the Hawaiian Islands according to the MOST model. Very good agreement (RMS differences at the level of few hundredths TEC units) is evident, the differences are mostly due to the different data filtering methods applied. Moreover, we see significant TIDs for 5 satellites (PRNs 4, 7, 8, 10, 20) at different times due to the different locations of the ionospheric piercing points (IPPs) and the subionospheric points (SIPs : IPPs projections onto the ellipsoid). In particular, for the satellite PRN 10 the TEC perturbation occurred before the tsunami reached the Hawaiian Islands; this is in fact due to the geometry corresponding to the particular elevation and azimuth angles of satellite PRN 10 as the tsunami-generated TIDs were detected when tsunami the wave front was still about 150 km away from the coast. For satellites PRN 13 and 23 no significant TIDs were detected, likely due to elevations and azimutal positions with respect to the tsunami as a possible cause of the TIDs.
The TEC variations are computed for 7 satellites (PRNs 4, 7, 8, 10, 13, 20, 23) in view from the AHUP station on the Hawaiian Islands (latitude: 19.379 degrees, longitude: −155.266 degrees, height: 1104.881 meters). The black vertical line represents the time when the tsunami reached the Hawaiian Islands. TIDs were clearly detected, with good agreement between the two approaches.
Can we detect TIDs induced by the tsunami itself ? If this could be confirmed, the potential of real-time detection of TIDs would be evident.
At first, we performed a wavelet analysis using the Paul wavelet (that gives better time localization than the Morlet one) and we determine both the dominant modes of variability and how those modes vary in time46. This technique allows us to highlight and evaluate the TID wave periods. Here, the wavelet analysis has been performed in python using scripts running the wavelet software provided by C. Torrence and G. Compo, and available at http://atoc.colorado.edu/research/wavelets/. We processed 260 sTEC time series, for all the satellites in view at the 56 GPS permanent stations. We found periods in the range of 10 to 30 minutes, similar to the periods of the tsunami ocean waves, which can range from 5 min up to an hour with the typical deep ocean period of only 10–30 wavelengths around 400 km, and the velocity approximately 200 m/s4.
Figures 3 and 4 show the sTEC time series wavelet analysis for the 7 satellites in view at the station AHUP. The upper panels show the sTEC time series obtained with the VARION software in a real-time scenario, as plotted in Fig. 2. The bottom panels indicate the wavelet spectra. The colors represent the intensity of the power spectrum and the black contour encloses regions of greater than 95% of confidence for a red noise process. We can identify 5 satellites (PRNs 4, 7, 8, 10, 20) with peaks consistent in time and period with the tsunami ocean waves. These results clearly show TIDs appearing after the tsunami reached the islands.
(a,b,e,f) Four of 260 time series used for the wavelet analysis, station AHUP, satellite PRN 4, 7, 8, 10. (c,d,g,h) The wavelet power spectrum used the Paul wavelet. The vertical axis displays the Fourier period (in min), the horizontal axis is time (s). The black vertical line represents the time when the tsunami reached the Hawaiian islands. The color panels represent the intensity of the power spectrum; the black contour encloses regions of greater than 95% confidence for a red-noise process with a lag-1 coefficient of 0.7246; the external black line indicates the “one of influence”, the limit outside of which edge effects may become significant. We clearly see the increase of the power spectrum for periods between 10 and 30 minutes during the TIDs.
(i,l,o) Three of 260 time series used for the wavelet analysis, station AHUP, satellite PRN 13, 20, 23. (m,n,p) The wavelet power spectrum used the Paul wavelet. The vertical axis displays the Fourier period (in min), the horizontal axis is time (s). The black vertical line represents the time when the tsunami reached the Hawaiian islands. For satellites PRN 13 and 23 we do not see significant increase of the power spectrum for periods between 10 and 30 minutes during the TIDs.
Figure 5 displays a map of the region around the Hawaiian Islands, the area of our focus in order to highlight the most significant sTEC variations. The colored tracks show the positions of the SIPs (equal to corresponding IPPs, when seen on the map) for each of the 7 satellites considered in Fig. 1 as seen from the 56 GPS permanent stations during an observation span of two hours (8:00 to 10:00 UT, 28 October 2012). The colors represent the variation in sTEC, obtained by VARION processing; the TIDs are clearly visible in the interval of significant sTEC variations (from positive to negative values and vice-versa).
The TIDs are clearly visible in the interval of significant sTEC variations (from positive to negative values and vice-versa). It is also shown that PRN 10 detected TIDs prior to the tsunami arrival at Hawaiian Islands (08:30:08 UT). The map has been generated using the matplotlib Basemap toolkit55.
Figure 6 shows time sTEC variations for two hours (08:00 to 10:00 UT - 28 October 2012) at the IPPs vs. distance from the Haida Gwaii earthquake epicenter, for the same 7 satellites under consideration. The TIDs are clearly visible in the interval of significant sTEC variations (from positive to negative values and vice-versa). The vertical and horizontal black lines represent the time (when the tsunami arrived at the Hawaiian Islands) and the distance (between the epicenter and the Big Island), respectively. In this way, we identify the green rectangle as the alert area and it is evident that satellite PRN 10, the closest to the earthquake epicenter detected TIDs before the tsunami arrived at Hawaiian Islands (08:30:08 UT). In the distance vs time plots (also called hodochrons) the slope of the straight line, fitted considering corresponding sTEC minima for different satellites, represents the horizontal speed estimate of TIDs. This plot indicates that the linear least-squares estimated speed of the TIDs is about 316 m/s and it is found to be in good agreement with a typical speed of the tsunami gravity waves estimated with ground-based GNSS receivers (see Appendix B). We note that such speed determinations via hodochron are not available in real-time, but neither are these estimates needed for real-time tsunami detection.
The TIDs are clearly visible in the interval of significant sTEC variations (from positive to negative values and vice-versa). The vertical and horizontal black lines represent the time (when the tsunami arrived at the Hawaiian Islands) and the distance (between the epicenter and the Big Island), respectively; it is evident that PRN 10 detected TIDs before the tsunami arrived at Hawaiian Hawaii Islands (08:30:08 UT). The slope of the straight line fitted, considering a linear least-squares regression for corresponding sTEC minima for different satellites, represent the TIDs mean propagation velocity.
Figure 7 displays a sequence of maps of the region around the Hawaiian Islands showing the variations in sTEC (determinable in real-time) at IPP/SPI locations on top of the MOST model sea-surface heights. Note that, just as the MOST model wavefronts are moving past the IPPs, the sTEC variations in the region become pronounced, correlated with the passage of the ocean tsunami itself. In particular, at 08:22:00 GPS time (08:21:44 UT) we are able to see sTEC perturbations from 56 stations looking at satellite PRN 10. The propagation of the MOST modeled tsunami passes the ionospheric pierce points located NW of the Big Island and offers insight with regard to the ionospheric response to the tsunami-driven atmospheric gravity wave. These perturbations are detected before the tsunami reached the islands as seen from the locations of the SIP points. The following frames indicate the tsunami-driven TIDs detected from the other 4 satellites (PRNs 4, 7, 8, 20) tracking the propagating tsunami (see supplementary video SV1).
TIDs are consistent in time and space with the tsunami waves. The maps have been generated using the matplotlib Basemap toolkit55.
Conclusion
We have found observational evidence of variations in GPS sTEC measurements in the range of 0.1–0.2 TEC units (on the order of 1% of the background TEC value) that are associated with the Haida Gwaii tsunami of 28 October 2012. We compared two independent signal processing techniques, one available in real-time and one available in post-processing, and a good agreement was found between the JPL (post-processed) and VARION (real-time capable) results. We performed a wavelet analysis and we observed sTEC variations with a typical period between 10 and 30 minutes, consistent with the ocean tsunami waves. We estimated the speed of the TIDs generated by the tsunami-driven IGWs and we found a typical speed of about 316 km/s. From the comparison between the MOST model results and TECs measurements we have validated our results in time and space. Using signals from 56 GPS stations located on the Hawaiian Islands, we have detected TEC perturbations before the actual tsunami arrival; this is due to the geometry of the satellite PRN 10 (elevation and azimuth angles) and so the position of the SIPs at that time.
We have demonstrated that the real-time capable VARION algorithm is able to detect the TIDs generated by tsunami-driven gravity waves and may be considered as a novel contribution to future integrated operational tsunami early warning systems.
We are currently implementing the VARION algorithm in JPL’s Global Differential GPS system (GDGPS) providing real-time access to 1-Hz data streams from about 230 global real-time stations collecting data from multiple constellations including GPS, Galileo, GLONASS and BeiDou. With real-time streams of data the polynomial fit has been implemented as a finite duration impulse response (FIR) high-pass filter. For our application, a FIR filter is designed with 2048 coefficients (taps), and so when using 1-Hz data there is an initial delay of 35 minutes (2048/3600*60). This period is called the transitory phase (TP). When TP ends, the system will proceed in stationary phase (SP) and will provide continuous real-time estimates of TEC perturbations. This initial delay will not be expected to affect the reliability of the system because it occurs once the receiver starts tracking the particular satellite and this will likely not coincide with start of the event.
A real-time tsunami detection system could be designed using VARION combined with real-time data from different sources (e.g. seismometers, buoys, GNSS receivers). Once an earthquake is detected in a specific location, such a system will begin processing the real-time TEC outputs using multiple stations located near the epicenter searching for ionospheric signals that may be correlated with the expected tsunami propagation. The measurements would be collected and processed by a central processing facility also providing risk assessments and maps related to a particular earthquake event. The use of multiple independent data types will be expected to contribute significantly to the robustness of the system.
Appendix A: VARION Methodology
The VARION approach is based on single time differences of geometry-free combinations of GPS carrier-phase measurements, using a standalone GPS receiver and standard GPS broadcast products (orbits and clocks corrections) that are available in real-time. We start from the carrier-phase observation, which in length units is

where i is the index of the signal frequency, subscript R refers to a particular receiver and superscript S refers to a satellite. λ is the carrier phase wavelength;  is the geometric range; c is the speed of light; δtR and δtS are the receiver and the satellite clock errors, respectively;
is the geometric range; c is the speed of light; δtR and δtS are the receiver and the satellite clock errors, respectively;  and
and  are the tropospheric and the ionospheric delays along the path from the satellite to the receiver, respectively;
are the tropospheric and the ionospheric delays along the path from the satellite to the receiver, respectively;  is the phase ambiguity;
is the phase ambiguity;  is the sum of the other effects (relativistic effects, phase center variations, and phase windup); and
is the sum of the other effects (relativistic effects, phase center variations, and phase windup); and  and
and  represent the multipath and the noise, respectively.
represent the multipath and the noise, respectively.
If no cycle slips occurred, the unknown carrier phase ambiguity can be considered constant between two consecutive epochs. The receiver and the satellite Inter-Frequency Biases (IFB) in the carrier-phase ionospheric obsevable are also assumed as constant for a given period47,48,49,50. For these reasons, differentiating (Equation 1) in time between two consecutive epochs (t and t + 1), and applying the geometry-free combination, we obtain the geometry-free time single-difference observation equation (Equation 2), with no need of estimate in real-time the phase ambiguity and the IFB.

where the subscript  refers to the geometry-free combination and f1 and f2 are the L1 and L2 frequencies, 1575.42 MHz and 1227.60 MHz respectively.
refers to the geometry-free combination and f1 and f2 are the L1 and L2 frequencies, 1575.42 MHz and 1227.60 MHz respectively.
Taking into account the ionospheric refraction along the geometric range, we compute the TEC variations between two consecutive epochs (Equation 3)

Subsequently, the TEC variations are integrated over the time interval (from  to
to  ) during which the tsunami event occurred, to retrieve tsunami ionospheric disturbances (Equation 4).
) during which the tsunami event occurred, to retrieve tsunami ionospheric disturbances (Equation 4).

We normally consider time intervals of 2 hours. In order to remove longer period variations in TEC time series (such as diurnal variations and multiple-hour trends due to changing elevation angle of the receiver-satellite line-of-sight), we used an  order polynomial to fit the TEC time series, and subtract the observed TEC values from the polynomial fit, with the residuals representing the variation in TEC due to a TID perturbation (see ref. 51 for detailed methodology).
order polynomial to fit the TEC time series, and subtract the observed TEC values from the polynomial fit, with the residuals representing the variation in TEC due to a TID perturbation (see ref. 51 for detailed methodology).
Concerning the geolocation of the TEC estimates, the VARION algorithm uses the Klobuchar broadcast ionospheric model, based on an ionosphere thin shell (in our case, at the height of 350 km) approximation52, enabling the real-time computation of both the positions of the ionospheric pierce points and the sub-ionospheric points (SIP: IPP projection onto the ellipsoid).
It is useful to underline that we considered the already presented technique based on double time differences of VTEC with intervals of 300 seconds53,54 and we believe that the main advantages of our VARION algorithm are the independence from cycle-slips (they are detected and removed as outliers), the true real-time TEC estimations and the very low computational time.
Appendix B: Ionospheric Height vs TID Velocity
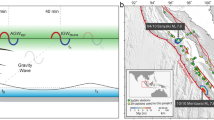
Under the flat Earth approximation, it is possible to show that there is a direct dependence of the TID estimated speed on the modeled ionospheric layer height. Taking into account Fig. 8, where the subscripts  and
and  represent estimated and real values, the estimated TID speed
represent estimated and real values, the estimated TID speed  using ground-based GNSS observations will not necessary be equal to the real TID speed
using ground-based GNSS observations will not necessary be equal to the real TID speed  . The two values are directly proportional as shown in Eqn. 5.
. The two values are directly proportional as shown in Eqn. 5.

where  represents the ratio between the modeled ionospheric height layer the height at which we have the maximum of the electron density, respectively.
represents the ratio between the modeled ionospheric height layer the height at which we have the maximum of the electron density, respectively.
In particular, the ionospheric shell height used in this case has a constant value of 350 km while the electron density profiles obtained using, e.g., the International Reference Ionosphere (IRI), a standard empirical model of the global ionosphere (available at http://omniweb.gsfc.nasa.gov/vitmo/iri_vitmo.html), indicates a maximum electron density value to occur at 300 km (see Supplementary Figure SF1). If we consider the TID speed to be almost equal to the tsunami speed, we can conclude that the best TID speed estimation using GNSS observations will be around 300 m/s.
Additional Information
How to cite this article: Savastano, G. et al. Real-Time Detection of Tsunami Ionospheric Disturbances with a Stand-Alone GNSS Receiver: A Preliminary Feasibility Demonstration. Sci. Rep. 7, 46607; doi: 10.1038/srep46607 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Daniels, F. B. Acoustic energy generated by ocean waves. d. Acoust. Soc. 24, 83 (1952).
Hines, C. O. Internal atmospheric gravity waves at ionospheric heights. Can. J. Phys. 38, 14411481, doi: 10.1139/p60-150 (1960).
Hines, C. O. Gravity waves in the atmosphere. Nature 239, 7378, doi: 10.1038/239073a0 (1972).
Peltier, W. R. & Hines, C. O. On the possible detection of tsunamis by a monitoring of the ionosphere. J. Geophys. Res. 81(12), 1995–2000 (1976).
Artru, J., Ducic, V., Kanamori, H., Lognonné, P. & Murakami, M. Ionospheric detection of gravity waves induced by tsunamis. Geophys. J. Int. 20, 840–848, doi: 10.1111/j.1365-246X.2005.02552.x (2005).
Rolland, L. M., Occhipinti, G., Lognonné, P. & Loevenbruck, A. Ionospheric gravity waves detected offshore hawaii after tsunamis. Geophys. Res. Lett. 37, L17101, doi: 10.1029/2010GL044479 (2010).
Galvan, D. A. et al. Ionospheric signatures of tohoku-oki tsunami of march 11, 2011: Model comparisons near the epicenter. Radio Sci. 47, RS4003 ,doi: 10.1029/2012RS005023 (2012).
Occhipinti, G., Lognonné, P., Kherani, E. A. & Hbert, H. Threedimensional waveform modeling of ionospheric signature induced by the 2004 sumatra tsunami. Geophys. Res. Lett. 33, L20104, doi: 10.1029/2006GL026865 (2006).
Mai, C.-L. & Kiang, J.-F. Modeling of ionospheric perturbation by 2004 sumatra tsunami. Radio Sci. 44, RS3011, doi: 10.1029/2008RS004060 (2009).
Lee, M. C. et al. Did tsunami-launched gravity waves trigger ionospheric turbulence over Arecibo? J. Geophys. Res. 113, A01302, doi: 10.1029/2007JA012615 (2008).
Coïsson, P., Lognonné, P., Walwer, D. & Rolland, L. M. First tsunami gravity wave detection in ionospheric radio occultation data. Earth and Space Science 2, 125–13, doi: 10.1002/2014EA000054 (2015).
Yang, Y.-M. et al. Tohoku-oki earthquake caused major ionospheric disturbances at 450 km altitude over alaska. Radio Sci. 49, 1206–1213, doi: 10.1002/2014RS005580 (2014).
Hung, R. J., Phan, T. & Smith, R. E. Observation of gravity waves during the extreme tornado outbreak of 3 april 1974. J. Atmos. Terr. Phys. 40, 831–843, doi: 10.1016/0021-9169(78)90033-8 (1978).
Kelley, M. C. In situ ionospheric observations of severe weather related gravity waves and associated small scale plasma structure. J. Geophys. Res. 102, 329–335, doi: 10.1029/96JA03033 (1997).
Xiao, Z., Xiao, S., Hao, Y. & Zhang, D. Morphological features of ionospheric response to typhoon. J. Geophys. Res. 112, A04304, doi: 10.1029/2006JA011671 (2007).
Richmond, A. D. & Matsushita, S. Thermospheric response to a magnetic substorm. J. Geophys. Res. 80, 2839–2850, doi: 10.1029/JA080i019p02839 (1975).
Nicolls, M. J., Kelley, M. C., Coster, A. J., González, S. A. & Makela, J. J. Imaging the structure of a large scale tid using isr and tec data. Geophys. Res. Lett. 31, L09812, doi: 10.1029/2004GL019797 (2004).
Calais, E. & Minster, J. B. GPS detection of ionospheric perturbations following the january 17, 1994, northridge earthquake. Geophys. Res. Lett. 22, 1045–1048, doi: 10.1029/95GL00168 (1995).
Artru, J., Lognonné, P. & Blanc, E. Normal modes modelling of post-seismic ionospheric oscillations. Geophys. Res. Lett. 28, 697700, doi: 10.1029/2000GL000085 (2001).
Kelley, M. C., Livingston, R. & McCready, M. Large amplitude thermospheric oscillations induced by an earthquake. Geophys. Res. Lett. 12, 577–580, doi: 10.1029/GL012i009p00577 (1985).
Tsugawa, T., Otsuka, Y., Coster, A. J. & Saito, A. Medium scale traveling ionospheric disturbances detected with dense and wide tec maps over north america. Geophys. Res. Lett. 34, L22101, doi: 10.1029/2007GL031663 (2007).
Occhipinti, G., Kherani, E. A. & Lognonné, P. Geomagnetic dependence of ionospheric disturbances induced by tsunamigenic internal gravity waves. Geophys. J. Int. 73, 753765, doi: 10.1111/j.1365-246X.2008.03760.x (2008).
Occhipinti, G. et al. Three-dimensional numerical modeling of tsunami-related internal gravity waves in the hawaiian atmosphere. Earth Planets Space 63(7), 847–851 (2011).
Hickey, M. P., Schubert, G. & Walterscheid, R. L. Propagation of tsunami-driven gravity waves into the thermosphere and ionosphere. J. Geophys. Res. 114, A08304, doi: 10.1029/2009JA014105 (2009).
Meng, X. et al. A new physics-based modeling approach for tsunami-ionosphere coupling. Geophys. Res. Lett. 42, 4736–4744, doi: 10.1002/2015GL064610 (2015).
Jin, S., Occhipinti, G. & Jin, R. Gnss ionospheric seismology: recent observation evidences and characteristics. Earth-Science Reviews 147, 54–64, doi: 10.1016/j.earscirev.2015.05.003 (2015).
Komjathy, A. et al. Review and perspectives: Understanding natural-hazards-generated ionospheric perturbations using GPS measurements and coupled modeling. Radio Sci. 51, 951–961, doi: 10.1002/2015RS005910 (2016).
Titov, V. V. et al. Real-time tsunami forecasting: Challenges and solutions. Nat. Hazards 35(1), 41–58 (2005).
Sardon, E. Z. N. & Rius, A. Tsunami forecasting, vol. 15, chap. 12, 371–400 (Harvard University Press, Cambridge, MA and London, England, 2009).
Wei, Y. et al. Real-time experimental forecast of the peruvian tsunami of august 2007 for u.s. coastlines. Geophys. Res. Lett. 35, L04609, doi: 10.1029/2007GL032250 (2008).
Wei, Y., Chamberlin, C., Titov, V., Tang, L. & Bernard, E. N. Modeling of the 2011 japan tsunami - lessons for near-field forecast. Pure Appl. Geophys. 170 (6–8), 1309–1331, doi:10.1007/s00024-012-0519-z (2013).
Tang, L. V. V. et al. Direct energy estimation of the 2011 japan tsunami using deep-ocean pressure measurements. J. Geophys. Res. 117, C08008, doi: 10.1029/2011JC007635 (2012).
Percival, D. B. et al. Extraction of tsunami source coefficients via inversion of DART® buoy data. Nat. Hazards 58(1), 567–590, doi: 10.1007/s11069-010-9688-1 (2011).
Colosimo, G., Crespi, M. & Mazzoni, A. Real-time GPS seismology with a stand-alone receiver: A preliminary feasibility demonstration. J. Geophys. Res. 116, B11 302, doi: 10.1029/2010JB007941 (2011).
Branzanti, M., Colosimo, G., Crespi, M. & Mazzoni, A. GPS near real-time coseismic displacements for the great tohoku-oki earthquake. IEEE Geoscience and Remote Sensing Letters, doi: 10.1109/LGRS.2012.2207704 (2012).
Benedetti, E. et al. Global navigation satellite systems seismology for the 2012mw6.1 emilia earthquake: Exploiting the vadase algorithm. Seism. Res. Lett. 85 no. 3, 649–656, doi: 10.1785/0220130094 (2014).
Komjathy, A., Sparks, L., Wilson, B. D. & Mannucci, A. J. Automated daily processing of more than 1000 ground-based GPS receivers for studying intense ionospheric storms. Radio Sci. 40, RS6006, doi:10.1029/2005RS003279 (2005).
Mannucci, A. J. et al. A global mapping technique for GPS derived ionospheric total electron content measurements. Radio Sci. 33, 565–582, doi: 10.1029/97RS02707 (1998).
Titov, V. V. & Synolakis, C. E. Modeling of breaking and non-breaking long-wave evolution and runup using vtcs-2. J. Waterway 121, 308–336(1995).
Titov, V. V. & Synolakis, C. E. Numerical modeling of tidal wave runup. J. Waterway 124(4), 157–171 (1998).
Burwell, D., C., A. & Tolkova, E. Diffusion and dispersion characterization of a numerical tsunami model. Ocean Modelling 19(1–2), 10–30 (2007).
Okada, Y. Surface deformation due to shear and tensile faults in a half space. Bull. Seismol. Soc. Am. 75 (4), 1135–1154 (1985).
Kajiura, K. Tsunami source, energy and directivity of wave radiation. Bull. Earthquake Res. Inst., Univ. Tokyo, 48, 835–869 (1970).
Mannucci, A. J. et al. GPS–based remote sensing of the geospace environment: Horizontal and vertical structure of the ionosphere and plasmasphere. Proc. SPIE Int. Soc. Opt. Eng. 5660, 1–13, doi: 10.1117/12.580048 (2004).
Yang, Y.-M. et al. The 2013 chelyabinsk meteor ionospheric impact studied using GPS measurements. Radio Sci. 49, 341350, doi: 10.1002/2013RS005344 (2014).
Torrence, C. & Compo, G. P. A practical guide to wavelet analysis. Bull. Amer. Meteor. Soc. 79, 6178 (1998).
Bishop, G., Walsh, D., Daly, P., Mazzella, A. & Holland, E. Analysis of the temporal stability of GPS and GLONASS group delay correction terms seen in various sets of ionospheric delay data. Proceedings of the 7th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1994) 1653–1661 (1994).
Sardon, E. Z. N. & Rius, A. Estimation of the transmitter and receiver differential biases and the ionospheric total electron content from global positioning system observations. Radio Sci 29, 577–586 (1994).
Brunini, C., B., W. & Meza, A. Temporal and spatial variability of the bias between topex- and GPS-derived total electron content. J Geod 79, doi: 10.1007/s00190-005-0448-z (2005).
Ciraolo, L., Azpilicueta, F., Brunini, C., Meza, A. & Radicella, S. M. Calibration errors on experimental slant total electron content (tec) determined with GPS. J Geodesydoi: 10.1007/s00190-006-0093-1 (2007).
Galvan, D. A., Komjathy, A., Hickey, M. P. & Mannucci, A. J. The 2009 samoa and 2010 chile tsunamis as observed in the ionosphere using GPS total electron content. J. Geophys. Res. 116, A06318, doi: 10.1029/2010JA016204 (2011).
Klobuchar, J. A. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Transactions on Aerospace and Electronic Systemsdoi: 10.1109/TAES.1987.310829 (1987).
Hernández-Pajares, M., Juan, J. M. & Sanz, J. Medium-scale traveling ionospheric disturbances affecting gps measurements: Spatial and temporal analysis. J. Geophys. Res. 111, A07S11, doi: 10.1029/2005JA011474 (2006).
Hernández-Pajares, M., Juan, J. M., Sanz, J. & Aragón-Àngel, A. Propagation of medium scale traveling ionospheric disturbances at different latitudes and solar cycle conditions. Radio Sci. 47, RS0K05, doi: 10.1029/2011RS004951 (2012).
Hunter, J. D. Matplotlib: A 2d graphics environment. Computing In Science & Engineering 9, 90–95(2007).
Acknowledgements
This research was partially developed thanks to the CNI (Consiglio Nazionale degli Ingegneri) and ISSNAF (Italian Scientists and Scholars in North America Foundation) fellowship granted to Mr. Giorgio Savastano for a two-months visit at NASA’s JPL (Jet Propulsion Laboratory, California Institute of Technology). In fact, VARION software was designed in 2015 at the University of Rome “La Sapienza”, Department of Civil, Building and Environmental Engineering, and subsequently, in 2016, further developed and validated in collaboration with the Ionospheric and Atmospheric Remote Sensing Group, Jet Propulsion Laboratory. The research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. We thank Dr. Yu-Ming Yang of JPL for providing us with GPS data in generating Figure 2 as well as expert advice during technical discussions. The authors would like also to thank the NOAA Center for Tsunami Research for providing access to the MOST model results for the 2012 Haida Gwaii event. Dr. Yong Wei’s work is funded by the Joint Institute for the Study of the Atmosphere and Ocean (JISAO) under NOAA Cooperative Agreement NA100AR4320148, JISAO Contribution 2016-01-48; PMEL Contribution 4574. Python wavelet software provided by Evgeniya Predybaylo based on Torrence and Compo (1998).
Author information
Authors and Affiliations
Contributions
G.S., A.M. and M.C. conceived the VARION algorithm, G.S. wrote the VARION software in python, G.S. and A.K. conducted the data processing. Y.W. provided the tsunami model. G.S., A.K., O.V. and M.C. analysed the results. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Savastano, G., Komjathy, A., Verkhoglyadova, O. et al. Real-Time Detection of Tsunami Ionospheric Disturbances with a Stand-Alone GNSS Receiver: A Preliminary Feasibility Demonstration. Sci Rep 7, 46607 (2017). https://doi.org/10.1038/srep46607
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep46607
This article is cited by
-
Machine learning-based detection of TEC signatures related to earthquakes and tsunamis: the 2015 Illapel case study
GPS Solutions (2024)
-
The JPL-GIM algorithm and products: multi-GNSS high-rate global mapping of total electron content
Journal of Geodesy (2024)
-
IROTI: a new index to detect and identify traveling ionospheric disturbances and equatorial plasma bubbles
GPS Solutions (2024)
-
Investigating Multiple Ionospheric Disturbances Associated with the 2020 August 4 Beirut Explosion by Geodetic and Seismological Data
Pure and Applied Geophysics (2024)
-
Using real GNSS data for ionospheric disturbance remote sensing associated with strong thunderstorm over Wuhan city
Acta Geodaetica et Geophysica (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.