Abstract
Hopping-type charge transport in an amorphous thin layer composed of organic molecules is simulated by the combined use of molecular dynamics, quantum chemical, and Monte Carlo calculations. By explicitly considering the molecular structure and the disordered intermolecular packing, we reasonably reproduce the experimental hole and electron mobilities and their applied electric field dependence (Poole–Frenkel behaviour) without using any adjustable parameters. We find that the distribution of the density-of-states originating from the amorphous nature has a significant impact on both the mobilities and Poole–Frenkel behaviour. Detailed analysis is also provided to reveal the molecular-level origin of the charge transport, including the origin of Poole–Frenkel behaviour.
Similar content being viewed by others
Introduction
Charge mobility μ in organic aggregates is a key factor in understanding the device performance of organic semiconductor devices such as organic light-emitting diodes (OLEDs)1,2,3. Typical organic layers of OLEDs are composed of amorphous thin films. Charge transport in amorphous organic solids is considered to occur through intermolecular charge hopping. Some models have been proposed to describe charge transport in amorphous organic solids. Among these models, the Gaussian disorder model4 successfully describes the macroscopic charge transport property. However, the model does not consider actual molecules and it has difficulty in revealing the molecular scale behaviour of carriers; the disorders, which originate from amorphous structures, are used as adjustable parameters to reproduce the experimental mobility data. Although microscopic analyses have also been carried out5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23 and some useful suggestions have been derived, we only have a limited understanding of the nature of charge transport in amorphous organic layers. In these studies, Marcus theory24 have frequently been employed to calculate rate constants kij of intermolecular charge transfer between molecule i and molecule j, described as:

Here, Hij is the electronic coupling between molecule i and j. ΔGij is the difference of Gibbs free energy between the initial and final states associated with the charge transfer from molecule i to j. λ is the reorganization energy, h is Planck constant, kB is Boltzmann constant, and T is the absolute temperature.
Our goals are to build a computational model reproducing the experimental μ quantitatively, and to gain understanding of the nature of charge transport in amorphous organic layers by analysing the model. We have recently carried out simulations in an amorphous organic solid23. The calculated μ was overestimated by two orders of magnitude, which also failed to reproduce the experimental observation that μ increased as the applied electric field F increased.
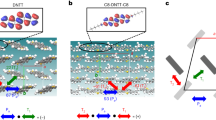
Here, charge transport process in an amorphous solid of 4,4′-bis(N-carbazolyl)-1,1′-biphenyl (CBP) (Supplementary Fig. S1), which is a typical host material for OLEDs, was investigated. In the calculations, we considered the energetic disorder (Fig. 1, see below for details) and intermolecular packing effect on λ, both of which were not included in a preceding paper23. An amorphous structure containing 4000 CBP molecules was generated using a molecular dynamics (MD) simulation. On the basis of the amorphous structure, Hij and λ were calculated by quantum chemical calculations. Reflecting the amorphous nature, the calculated Hij values were distributed as shown in Supplementary Figs S2 and S3. The “structural disorder” is often called the “off-diagonal disorder”. In the Gaussian disorder model4, material points on a cubic lattice are considered instead of real molecules, and the structural disorder is only an adjustable parameter to describe the experimental results. Here, real molecules are considered; not only the distribution of distances, but also the relative intermolecular orientation and the distribution of frontier orbitals contribute to the distribution of Hij. Examples of the intermolecular packing generated by the above-mentioned MD simulation are shown in Supplementary Fig. S4. From the examples and an intermolecular distance dependence of Hij (Supplementary Fig. S2), we find that Hij values are not solely determined by the intermolecular distances. In addition to the structural disorder, molecules (hopping sites) are distributed in energy in amorphous solids (Fig. 1), because different molecules undergo a different intermolecular interaction. The distribution of energy is called the “energetic disorder” or “diagonal disorder”. We calculated the energetic disorder by considering distributed electrostatic interaction with and polarization effect of neighbouring molecules. The energy of a hole/electron on molecule i,  , can be written as:
, can be written as:


Here, Iisolated and Aisolated are the ionization potential and electron affinity of an isolated CBP molecule, respectively.  ,
,  , and
, and  are the sum of electrostatic interaction with and polarization effect of neighbouring molecules, for positively charged, negatively charged, and the neutral state of molecule i, respectively. Therefore, ΔGij can be expressed as:
are the sum of electrostatic interaction with and polarization effect of neighbouring molecules, for positively charged, negatively charged, and the neutral state of molecule i, respectively. Therefore, ΔGij can be expressed as:

where ΔEk (k = i,j) is  or
or  for hole or electron transport, q is the charge of the carrier, F is an externally applied electric field (|F| = F) and xij is a vector connecting the centre of molecule i to the centre of molecule j (displacement of the carrier). The calculations in this study show that the distribution of the energy level was Gaussian (see Supplementary Fig. S5) and its sample standard deviation was 0.107 and 0.102 eV for the hole and electron, respectively. λ was calculated taking into account the steric influence of neighbouring molecules with the quantum mechanics / molecular mechanics method. Using the calculated Hij, ΔGij, and λ, kij were calculated from equation (1). The charge transport process was simulated using kinetic Monte Carlo method based on the MD-constructed amorphous structure and the kij, which provided the calculated μ (examples of calculated trajectories are shown in Supplementary Fig. S6). To confirm the validity of the calculations, we also performed time-of-flight (TOF) experiments. The experimental data were consistent with those reported previously20,25,26. More details of the computational and the experimental methods are shown later and and in the Supplementary Information.
for hole or electron transport, q is the charge of the carrier, F is an externally applied electric field (|F| = F) and xij is a vector connecting the centre of molecule i to the centre of molecule j (displacement of the carrier). The calculations in this study show that the distribution of the energy level was Gaussian (see Supplementary Fig. S5) and its sample standard deviation was 0.107 and 0.102 eV for the hole and electron, respectively. λ was calculated taking into account the steric influence of neighbouring molecules with the quantum mechanics / molecular mechanics method. Using the calculated Hij, ΔGij, and λ, kij were calculated from equation (1). The charge transport process was simulated using kinetic Monte Carlo method based on the MD-constructed amorphous structure and the kij, which provided the calculated μ (examples of calculated trajectories are shown in Supplementary Fig. S6). To confirm the validity of the calculations, we also performed time-of-flight (TOF) experiments. The experimental data were consistent with those reported previously20,25,26. More details of the computational and the experimental methods are shown later and and in the Supplementary Information.
Figure 2 compares the experimentally-obtained and the calculated μ for the hole and electron transport. The experimental μ (black filled and black open symbols in Fig. 2) shows a positive linear F1/2-dependence, often called Poole–Frenkel (PF)-type behaviour, commonly observed in organic amorphous materials1,4,27. Open circles in Fig. 2 consider the intermolecular packing effect in the calculations of λ but the energetic disorder is not considered. Here, the λ including the intermolecular packing effect in amorphous aggregates is denoted by λaggr. The calculated μ significantly deviate from the experimental values, being one or two orders of magnitude larger. In addition, the calculated negative F1/2-dependence is not compatible with the experiments. Open squares in Fig. 2 show the calculated μ incorporating the energetic disorder but the intermolecular packing effect on λ is not considered (calculated reorganization energy is noted as λisolated). By considering the energetic disorder, the experimentally-obtained positive F1/2-dependence is reproduced. The μ is more than one order of magnitude smaller compared with the experiments for electron transport. By incorporating both the energetic disorder and the intermolecular packing effect on λ, we obtain the filled squares in Fig. 2. The calculated μ showed a better agreement with the experimentally-obtained values. A slightly worse agreement for electron transport is proposed to reflect the difficulty in calculating unoccupied orbitals.
Calculated and experimental μ in an amorphous CBP film.
(a) For hole transport. (b) For electron transport. Black filled diamonds: measured by TOF experiments. Black open diamonds, downward triangles, and upward triangles: experimental data from Refs 20, 25 and 26, respectively. Open circles: calculated with λaggr and without energetic disorder (e. d.). Filled squares: calculated with λaggr and with e. d. Open squares: calculated with λisolated and with e. d.
We investigate the origin of the PF behaviour, the positive F1/2-dependence of μ. Figure 2 shows that the PF behaviour is reproduced when the energetic disorder is incorporated in the simulations, but not reproduced when the energetic disorder is not incorporated. Therefore, the energetic disorder plays a crucial role in the PF behaviour. To investigate the mechanism of influence of the energetic disorder on the F1/2-dependence of μ, we calculated the number of hops during the transport n, the number of hopping sites used at least once during the transport ν, and the mean time required for each individual charge hopping τ = t/n (t is the time required for the charge transport between electrodes), with and without the energetic disorder (see Table 1. The intermolecular packing effect on λ is considered in all cases.). When the energetic disorder is included in the simulations, n decreases by two orders of magnitude with F1/2 increasing from 300 V1/2cm−1/2 to 1300 V1/2cm−1/2, while τ has the same order of magnitude regardless of F. Since μ = L/(tF) = L/(nτF), the PF behaviour is mainly attributed to the decrease in n with F. Here, L is the distance between the electrodes. When F1/2 = 300 V1/2cm−1/2 and under the existence of the energetic disorder, n is larger than ν by two orders of magnitude, indicating that the same sites are repeatedly used. Hence, the charge carriers frequently move back and forth during the charge transport. This “round-trip” of carriers is enhanced by the energetic disorder: without the energetic disorder, n has the same order as or is one order of magnitude larger than that of ν. Different from the case of F1/2 = 300 V1/2cm−1/2, the differences of n and ν are much smaller when F1/2 = 1300 V1/2cm−1/2, regardless of whether the energetic disorder is incorporated or not. In summary, the energetic disorder causes frequent back and forth hopping of carriers and entails large n under weak F, but not under strong F. This results in the PF behaviour. When we compare the simulations with and without the energetic disorder under the same F1/2, not only n but also τ become larger by incorporation of the energetic disorder. Both factors affect the reduced μ for the case with energetic disorder. When we compare hole and electron transport with the same F1/2 and energetic disordered state, n and ν are not significantly different but τ is one to two orders of magnitude larger for electron transport. The larger τ induces a smaller μ for electrons in spite of the maximum Hij for electron transports (70 meV) being larger than that of hole transports (41 meV). This implies that μ is not solely determined by the largest Hij.
These characteristics can be explained at the molecular level. Figure 3 shows the number of hops into site i (here, we call it  ) versus their site energies
) versus their site energies  . When F1/2 = 300 V1/2cm−1/2,
. When F1/2 = 300 V1/2cm−1/2,  is nearly exponential with the site energies, indicating that the charges mainly use “low-energy” sites (black filled area in Fig. 1) during the transport, that is, charge carriers tend to jump into “low-energy” hopping sites. Here, we note that the “low-energy” site for hole (electron) has a positively (negatively) high energy for the hopping site, as shown in Fig. 1. When the charge carriers escape from the low-energy hopping sites, they tend to back into the low-energy sites owing to the difference of the site energies. Hence, the charge carriers frequently move forward and backward between the low-energy sites and the neighbouring sites under F1/2 = 300 V1/2cm−1/2.
is nearly exponential with the site energies, indicating that the charges mainly use “low-energy” sites (black filled area in Fig. 1) during the transport, that is, charge carriers tend to jump into “low-energy” hopping sites. Here, we note that the “low-energy” site for hole (electron) has a positively (negatively) high energy for the hopping site, as shown in Fig. 1. When the charge carriers escape from the low-energy hopping sites, they tend to back into the low-energy sites owing to the difference of the site energies. Hence, the charge carriers frequently move forward and backward between the low-energy sites and the neighbouring sites under F1/2 = 300 V1/2cm−1/2.
The small number of low-energy sites significantly decreases μ under weak F as demonstrated in the following manner. Figure 4 shows μ versus F1/2 with low-energy 1%, 3%, and 5% of all sites removed. From Fig. 4, μ is found to be significantly influenced by the small number (1–5%) of low-energy sites when F1/2 = 300 V1/2cm−1/2: it is often considered that low-energy sites trap carriers. Our results suggest that carriers hop back and forth between low-energy sites and the neighbouring sites. The carriers are not frozen in the low-energy sites, but the “round-trip” of carriers consequently consumes much time; therefore, this may also be comprehended as a kind of “trap”.
On the contrary, when F1/2 = 1300 V1/2cm−1/2, the correlation between  and the site energy is weak [Fig. 3(c)]. Figure 4 clearly shows that μ does not change irrespective of the existence of low-energy sites at F1/2 = 1300 V1/2cm−1/2, indicating that these sites do not work as “traps”. Charge carriers tend to move along with F regardless of the energetic disorder.
and the site energy is weak [Fig. 3(c)]. Figure 4 clearly shows that μ does not change irrespective of the existence of low-energy sites at F1/2 = 1300 V1/2cm−1/2, indicating that these sites do not work as “traps”. Charge carriers tend to move along with F regardless of the energetic disorder.
Next, we discuss the influence of Hij distribution on μ. Hij was distributed over the range of 0 to 41 meV and 0 to 70 meV for the hole and electron, respectively (Supplementary Fig. S3). The kinetic Monte Carlo simulations were also performed without molecular pairs with Hij < 0.1, 1.0, 2.0 and 3.0 meV, and the calculated μ are shown in Fig. 5. The molecular pairs with Hij < 0.1 meV do not affect the charge transports (open circles in Fig. 5 are overlapped with filled squares). However, the contributions of the pairs with Hij < 1.0, 2.0 and 3.0 meV are significant, especially at strong F. When the pairs with Hij < 3.0 meV are removed (downward open triangles in Fig. 5), μ decreases by three or four orders of magnitude. This result clearly shows that the pairs with Hij < 3.0 meV are frequently used as charge hopping sites although the Hij values are much smaller than the maximum Hij (41 meV and 70 meV for hole and electron hopping, respectively). Hence, the decrease in μ by removing pairs with Hij < 1.0–3.0 meV is attributed to the change in charge transport paths. This result indicates that in amorphous aggregates, weakly coupled pairs significantly contribute to μ by forming effective charge transport paths especially at strong F.
μ calculated under various conditions.
(a) For hole. (b) For electron. Filled squares: all the pairs are used. Open circles (overlapped with filled squares): pairs with Hij < 0.1 meV are removed. Open diamonds: pairs with Hij < 1.0 meV are removed. Upward open triangles: pairs with Hij < 2.0 meV are removed. Downward open triangles: pairs with Hij < 3.0 meV are removed.
From the above discussion, in amorphous thin layers, μ is not simply determined by the maximum Hij and therefore the maximum kij, although the values of μ are often discussed by the Hij or kij. This feature is different from that of crystalline solids. Thus, consideration of different hierarchical structures is crucial for the understanding of μ in amorphous organic aggregates.
In conclusion, μ was quantitatively reproduced without any adjustable parameters, by taking into account both the disorder of the energy level of the hopping sites and the disordered structure. The PF behaviour was also reproduced, and its origin was attributed to the influence of the energetic disorder on the charge transport trajectory: under weak F, charge carriers go back and forth owing to the difference of the site energies; however, under strong F, charge carriers tend to move simply along F. In amorphous organic solids, molecular pairs with relatively small Hij are found to largely contribute to μ, indicating that they form effective paths for charge transport.
Methods
Simulation of charge transport process
Simulations of the charge transport process for amorphous structure containing 100, 1000, 4000, and 8000 molecules of CBP were performed. The results for the 4000 CBP system are provided in the main text. The MD simulation was performed on LAMMPS program package28. Density functional theory and extended Hückel calculations were carried out using the Gaussian 09 program package29. Kinetic Monte Carlo simulations were performed using our in-house program. Details of methodology are described in Supplementary Information.
Experimental TOF measurement
μ was experimentally measured for a CBP thin film using TOF apparatus (TOF-401-3, Sumitomo Heavy Industries Advanced Machinery Co., Ltd., Japan). A TOF sample with the structure of ITO (50 nm)/CBP (3.9 μm)/Al (20 nm) was fabricated by vacuum-deposition. A N2 gas laser (KEC-150, Usho Optical Systems Co., Ltd., Japan) with a wavelength of 337 nm was used to generate the photocarriers.
Additional Information
How to cite this article: Uratani, H. et al. Detailed analysis of charge transport in amorphous organic thin layer by multiscale simulation without any adjustable parameters. Sci. Rep. 6, 39128; doi: 10.1038/srep39128 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Coropceanu, V. et al. Charge transport in organic semiconductors. Chem. Rev. 107, 926–952 (2007).
Tang, C. W. & VanSlyke, S. A. Organic electroluminescent diodes. Appl. Phys. Lett. 51, 913–915 (1987).
Adachi, C., Tsutsui, T. & Saito, S. Organic electroluminescent device having a hole conductor as an emitting layer. Appl. Phys. Lett. 55, 1489–1491 (1989).
Bässler, H. Charge transport in disordered organic photoconductors a Monte Carlo simulation study. Phys. Status Solidi B 175, 15–56 (1993).
Cornil, J., Beljonne, D., Calbert, J. P. & Brédas, J.-L. Interchain interactions in organic π-conjugated materials: Impact on electronic structure, optical response, and charge transport. Adv. Mater. 13, 1053–1067 (2001).
Brédas, J.-L., Calbert, J. P., da Silva Filho, D. A. & Cornil, J. Organic semiconductors: A theoretical characterization of the basic parameters governing charge transport. Proc. Natl. Acad. Sci. USA 99, 5804–5809 (2002).
Lin, B. C., Cheng, C. P., You, Z.-Q. & Hsu, C.-P. Charge transport properties of tris(8-hydroxyquinolinato)aluminum(III): Why it is an electron transporter. J. Am. Chem. Soc. 127, 66–67 (2005).
Hutchison, G. R., Ratner, M. A. & Marks, T. J. Intermolecular charge transfer between heterocyclic oligomers. Effects of heteroatom and molecular packing on hopping transport in organic semiconductors. J. Am. Chem. Soc. 127, 16866–16881 (2005).
Kirkpatrick, J. & Nelson, J. Theoretical study of the transfer integral and density of states in spiro-linked triphenylamine derivatives. J. Chem. Phys. 123, 084703 (2005).
Li, H., Brédas, J.-L. & Lennartz, C. First-principles theoretical investigation of the electronic couplings in single crystals of phenanthroline-based organic semiconductors. J. Chem. Phys. 126, 164704 (2007).
Datta, A., Mohakud, S. & Pati, S. K. Electron and hole mobilities in polymorphs of benzene and naphthalene: Role of intermolecular interactions. J. Chem. Phys. 126, 144710 (2007).
Kwiatkowski, J. J. et al. Simulating charge transport in tris(8-hydroxyquinoline) aluminium (Alq3). Phys. Chem. Chem. Phys. 10, 1852–1858 (2008).
Nagata, Y. & Lennartz, C. Atomistic simulation on charge mobility of amorphous tris(8-hydroxyquinoline) aluminum (Alq3): Origin of Poole–Frenkel–type behavior. J. Chem. Phys. 129, 034709 (2008).
Lukyanov, A., Lennartz, C. & Andrienko, D. Amorphous films of tris(8-hydroxyquinolinato)aluminium: Force-field, morphology, and charge transport. Phys. Status Solidi A 206, 2737–2742 (2009).
Yamada, T., Sato, T., Tanaka, K. & Kaji, H. Percolation paths for charge transports in N,N′-diphenyl-N,N′-di(m-tolyl)benzidine (TPD). Org. Electron. 11, 255–265 (2010).
Difley, S., Wang, L.-P., Yeganeh, S., Yost, S. R. & Voorhis, T. V. Electronic properties of disordered organic semiconductors via QM/MM simulations. Acc. Chem. Res. 43, 995–1004 (2010).
MacKenzie, R. C. I., Frost, J. M. & Nelson, J. A numerical study of mobility in thin films of fullerene derivatives. J. Chem. Phys. 132, 064904 (2010).
Yamada, T. et al. Revealing bipolar charge-transport property of 4,4′-N,N′-dicarbazolylbiphenyl (CBP) by quantum chemical calculations. Org. Electron. 12, 169–178 (2011).
Rüchle, V. et al. Microscopic simulations of charge transport in disordered organic semiconductors. J. Chem. Theory Comput. 7, 3335–3345 (2011).
Li, H. et al. Experimental and theoretical study of the charge transport property of 4,4′-N,N′-dicarbazole-biphenyl. Sci. China Chem. 55, 2428–2432 (2012).
May, F. et al. Design rules for charge-transport efficient host materials for phosphorescent organic light-emitting diodes. J. Am. Chem. Soc. 134, 13818–13822 (2012).
Friederich, P., Symalla, F., Meded, V., Neumann, T. & Wenzel, W. Ab initio treatment of disorder effects in amorphous organic materials: Toward parameter free materials simulation. J. Chem. Theory Comput. 10, 3720–3725 (2014).
Suzuki, F. et al. Multiscale simulation of charge transport in a host material, N,N′-dicarbazole-3,5-benzene (mCP), for organic light-emitting diodes. J. Mater. Chem. C 3, 5549–5555 (2015).
Marcus, R. A. & Sutin, N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta 811, 265–322 (1985).
Matsushima, H., Naka, S., Okada, H. & Onnagawa, H. Organic electrophosphorescent devices with mixed hole transport material as emission layer. Curr. Appl. Phys. 5, 305–308 (2005).
Matsusue, N., Suzuki, Y. & Naito, H. Charge carrier transport in neat thin films of phosphorescent iridium complexes. Jpn. J. Appl. Phys. 44, 3691 (2005).
Gill, W. D. Drift mobilities in amorphous charge-transfer complexes of trinitrofluorenone and poly-n-vinylcarbazole. J. Appl. Phys. 43, 5033–5040 (1972).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Frisch, M. J. et al.Gaussian 09, Revision C.01 and D.01. Gaussian, Inc., Wallingford CT, 2009.
Acknowledgements
The computation time on a supercomputer system was provided by the Institute for Chemical Research, Kyoto University, Japan, and the Academic Center for Computing and Media Studies (ACCMS), Kyoto University, Japan. This work was partly supported by JSPS KAKENHI Grant Number 25248053.
Author information
Authors and Affiliations
Contributions
H.K. planned and supervised the project. H.U. and S.K. performed the charge transport simulations. H.K., K.S., and F.S. supervised the simulations. T.F. performed TOF experiments and H.K. supervised them. H.U., S.K., and H.K. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Uratani, H., Kubo, S., Shizu, K. et al. Detailed analysis of charge transport in amorphous organic thin layer by multiscale simulation without any adjustable parameters. Sci Rep 6, 39128 (2016). https://doi.org/10.1038/srep39128
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep39128
This article is cited by
-
An efficient solid-solution crystalline organic light-emitting diode with deep-blue emission
Nature Photonics (2023)
-
Parameter-Free Multiscale Simulation Realising Quantitative Prediction of Hole and Electron Mobilities in Organic Amorphous System with Multiple Frontier Orbitals
Scientific Reports (2018)
-
Effects of Structural and Energetic Disorders on Charge Transports in Crystal and Amorphous Organic Layers
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

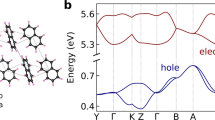



 versus their site energies.
versus their site energies. and
and  , respectively.
, respectively.
