Abstract
We formulate the Frobenius-norm-based measures for quantum coherence and asymmetry respectively. In contrast to the resource theory of coherence and asymmetry, we construct a natural measure of quantum coherence inspired from optical coherence theory while the group theoretical approach is employed to quantify the asymmetry of quantum states. Besides their simple structures and explicit physical meanings, we observe that these quantities are intimately related to the purity (or linear entropy) of the corresponding quantum states. Remarkably, we demonstrate that the proposed coherence quantifier is not only a measure of mixedness, but also an intrinsic (basis-independent) quantification of quantum coherence contained in quantum states, which can also be viewed as a normalized version of Brukner-Zeilinger invariant information. In our context, the asymmetry of N-qubit quantum systems is considered under local independent and collective  transformations. In- triguingly, it is illustrated that the collective effect has a significant impact on the asymmetry measure and quantum correlation between subsystems plays a non-negligible role in this circumstance.
transformations. In- triguingly, it is illustrated that the collective effect has a significant impact on the asymmetry measure and quantum correlation between subsystems plays a non-negligible role in this circumstance.
Similar content being viewed by others
Introduction
In the 20th century, quantum mechanics, as the core of quantum physics, is undoubtedly one of the most profound scientific theories during the development process of modern science and philosophy. Notably, quantum coherence is one of the most remarkable and characteristic traits of quantum mechanics and also viewed as the critical resource for the emerging field of quantum technologies, such as quantum cryptography1, quantum metrology2 and quantum computation3. This intrinsic principle of quantum mechanics enforces its entire departure from classical lines of thought, similar to the notion of quantum entanglement4. In different occasions, the generalized concept of quantum coherence manifests itself as quantum superposition, quantum asymmetry or non-commutability. These specific notions have gotten extensive applications in quantum physics both theoretically and experimentally. Therefore, the characterization, quantification and application of quantum coherence are one of the central topics in quantum information science.
Although the investigation of coherence theory has a long history in classical and quantum optics5,6,7,8,9, it does not provide an integrated and unified framework for quantitative study. In some contexts, even conflicting definitions have appeared with respect to the same concept10,11,12,13,14,15, especially when the vectorial character of electromagnetic waves is involved. From the perspective of quantum information theory, a rigorous framework for the characterization and quantification of coherence has been formulated very recently, based on the quantum resource theory16,17. On one hand, Baumgratz et al. defined the incoherent states and incoherent operations and further discussed the quantum coherence monotones in the constraint of a series of axiomatic-like prerequisites18, which is extremely similar to the approach adopted in quantum entanglement theory19. Within this framework, novel measures of quantum coherence have been proposed and the connections between coherence and other manifestations of quantum correlations have been carefully scrutinized20,21,22,23,24,25,26,27,28,29,30,31. On the other hand, Marvian and his collaborators proposed the resource theory of asymmetry which included the former notion of quantum coherence as a special case32,33,34,35,36,37. Moreover, the internal relations between these two approaches and their physical justifications have been further clarified lately38,39.
However, the story has never come to the end. The investigation of quantum coherence is now facing several crucial problems that need to be solved urgently. First of all, we should further identify the application scopes and physical meanings of existing measures of quantum coherence. In particular, the quantifiers presented in ref. 18 are established in the finite-dimensional setting and thus can not be directly applied to the infinite-dimensional systems. Moreover, explicit physical (or operational) meanings of existing measures of quantum coherence are to be pursued by the community, though partial results have been obtained31,40,41. Secondly, as indicated by Marvian et al., distinct approaches of quantifying quantum coherence will lead to different conclusions in a diverse set of tasks. For instance, the speakable notions of coherence may not be suitable to characterize the consumed resource in the task of phase estimation37,38. Moreover, Chitambar et al. also pointed out that all currently proposed basis-dependent theories fail to satisfy a criterion of physical consistency39. In addition, the interactions between quantum coherence and other manifestations of quantum correlations still need to be uncovered22,23. Finally, the quantitative relations between quantum coherence and other important quantities in quantum information are yet to be established42,43.
In contrast to the resource-theory framework, we notice that other types of coherence or asymmetry measures are also of great significance in optical coherence theory and condensed matter physics. For example, a measure of first-order coherence  (for qubit subsystem) was exploited to introduce the concept of accessible coherence44 and it was recently demonstrated that
(for qubit subsystem) was exploited to introduce the concept of accessible coherence44 and it was recently demonstrated that  can be unveiled from hidden coherence in partially coherent light45. Moreover, Fang et al. proposed a novel measure of the degree of symmetry by virtue of group theoretical approach and showed that this quantity can effectively detect the phenomena of accidental degeneracy and spontaneous symmetry breaking46. In this work, we formulate two Frobenius-norm-based measures by further extending their previous work and more importantly, illustrate the clear physical meanings of these quantifiers. Through the establishment of relationship with other significant physical quantities (e.g., Brukner-Zeilinger information), we emphasize that the purity of quantum states is not only a measure of mixedness, but also a basis-independent quantification of quantum coherence contained in quantum states.
can be unveiled from hidden coherence in partially coherent light45. Moreover, Fang et al. proposed a novel measure of the degree of symmetry by virtue of group theoretical approach and showed that this quantity can effectively detect the phenomena of accidental degeneracy and spontaneous symmetry breaking46. In this work, we formulate two Frobenius-norm-based measures by further extending their previous work and more importantly, illustrate the clear physical meanings of these quantifiers. Through the establishment of relationship with other significant physical quantities (e.g., Brukner-Zeilinger information), we emphasize that the purity of quantum states is not only a measure of mixedness, but also a basis-independent quantification of quantum coherence contained in quantum states.
Results
Coherence measure based on Frobenius norm
In the famous work of Mandel and Wolf, they introduced an important measure depicting the degree of polarization for planar electromagnetic fields7

where Φ2 represents 2 × 2 equal-time coherence matrix at a given point  and
and  , i, j = x, y. Note that this quantity characterizes the coherence between two mutually orthogonal components of the complex electric vector E(t) = [Ex(t), Ey(t)]T. Be aware of the Hermiticity and non-negativity of the matrix Φ2, we can define a physically valid quantum state ρ = Φ2/TrΦ2. Since the Bloch sphere is analogous to the Poincaré sphere,
, i, j = x, y. Note that this quantity characterizes the coherence between two mutually orthogonal components of the complex electric vector E(t) = [Ex(t), Ey(t)]T. Be aware of the Hermiticity and non-negativity of the matrix Φ2, we can define a physically valid quantum state ρ = Φ2/TrΦ2. Since the Bloch sphere is analogous to the Poincaré sphere,  can be rewritten as
can be rewritten as

where we have used the Bloch representation  and
and  are eigenvalues of ρ. It is apparent that
are eigenvalues of ρ. It is apparent that  is equivalent to the degree of first-order coherence
is equivalent to the degree of first-order coherence  adopted in refs 44,45 and exactly equal to the length of the Bloch vector
adopted in refs 44,45 and exactly equal to the length of the Bloch vector  . In fact, in this case (e.g., for qubit system) ρ can also be recast as
. In fact, in this case (e.g., for qubit system) ρ can also be recast as

with  and
and  .
.
Furthermore, Setälä et al. moved a step forward and extended the above 2D formalism into the formulation of the 3D degree of polarization coherence for arbitrary electromagnetic fields47,48, that is

where Φ3 denotes the 3 × 3 coherence matrix at a given point  and
and  , i, j = x, y, z. Similarly, by redefining ρ = Φ3/Tr Φ3, we obtain
, i, j = x, y, z. Similarly, by redefining ρ = Φ3/Tr Φ3, we obtain

Actually, we observe that this formalism can be unified and generalized to arbitrary dimensional systems, motivated by the work of Luis49, where a 4 × 4 density matrix was considered. The key idea is to quantify quantum coherence from the geometrical point of view, that is, the degree of coherence between distinct variables of optical fields is assessed as the distance between the coherence matrix and the identity matrix. Note that this geometrical approach is also employed in quantum resource theories16,17,18,19. Here the identity matrix, or maximally mixed state in the sense of quantum information, is identified as the fully incoherent and completely unpolarized light7,49. Therefore, we can construct the following general measure

where d is the dimension of the Hilbert space,  denotes the maximally mixed state. and the Frobenius norm is given by
denotes the maximally mixed state. and the Frobenius norm is given by  . Note that here the Frobenius norm is normalized to guarantee
. Note that here the Frobenius norm is normalized to guarantee  (see Methods section for more details). It is worth pointed out that this measure inherently possesses the following desirable properties:
(see Methods section for more details). It is worth pointed out that this measure inherently possesses the following desirable properties:
-
i
When d = 2, 3, 4, the coherence measure6 reduces to the existing quantifiers for 2D, 3D and 4D cases, where for 4D formalism, this measure was also termed as the depolarization index50,51.
-
ii
No optimization is involved in
 , which is in sharp contrast to the coherence measures proposed in ref. 18, though the optimization is rather straightforward there.
, which is in sharp contrast to the coherence measures proposed in ref. 18, though the optimization is rather straightforward there. -
iii
 is independent of the specific representation of ρ, that is,
is independent of the specific representation of ρ, that is,  is basis-independent.
is basis-independent. -
iv
 is unitarily invariant, since
is unitarily invariant, since  owing to the fact that the maximally mixed state
owing to the fact that the maximally mixed state  is the only state that remains invariant under arbitrary unitary transformation. In fact, the property (iv) is equivalent to (iii).
is the only state that remains invariant under arbitrary unitary transformation. In fact, the property (iv) is equivalent to (iii). -
v
 has an analytical expression and explicit geometrical interpretation. As we shall see below,
has an analytical expression and explicit geometrical interpretation. As we shall see below,  also has a clear operational meaning.
also has a clear operational meaning.
To further elaborate on the characteristics of  , we first present several observations where this coherence measure is involved.
, we first present several observations where this coherence measure is involved.
Observation I: Straightforward calculation shows that the square of  is directly proportional to the celebrated Brukner-Zeilinger invariant information52
is directly proportional to the celebrated Brukner-Zeilinger invariant information52

where the Brukner-Zeilinger information  is an operational notion defined as the sum of individual measures of information over a complete set of mutually complementary observables (MCO)53
is an operational notion defined as the sum of individual measures of information over a complete set of mutually complementary observables (MCO)53

Here i = 1, …, m and j = 1, …, d label complementary observables and their eigenvectors, respectively. A significant feature of  is its independence of the specific choice of the measured set of MCO and this independence is also equivalent to the unitary invariance of
is its independence of the specific choice of the measured set of MCO and this independence is also equivalent to the unitary invariance of  , since the unitary transformations do not alter the eigenvalues of ρ and Trρ2 only relies on them. Therefore, it is evident that
, since the unitary transformations do not alter the eigenvalues of ρ and Trρ2 only relies on them. Therefore, it is evident that  (and
(and  ) is a measure of basis-independent coherence contained in quantum states and quantifies the intrinsic randomness irrespective of the amount of entanglement between subsystems (if there are any). It is worth noting that the (global) purity does not solely determine the entanglement of a multi-partite state and this fact led to the investigation of the so-called maximally entangled mixed states for a given degree of purity54,55. Moreover, all pure states should always be represented as a coherent superposition of a certain set of basis states rather than a classical mixing and by our definition
) is a measure of basis-independent coherence contained in quantum states and quantifies the intrinsic randomness irrespective of the amount of entanglement between subsystems (if there are any). It is worth noting that the (global) purity does not solely determine the entanglement of a multi-partite state and this fact led to the investigation of the so-called maximally entangled mixed states for a given degree of purity54,55. Moreover, all pure states should always be represented as a coherent superposition of a certain set of basis states rather than a classical mixing and by our definition  for any pure state. This is reminiscent of the argument by von Neumann that the entropy of all pure states is defined to be 0 as a kind of normalization56. Finally, since the Brukner-Zeilinger invariant information was successfully utilized in quantum teleportation57, state estimation58 and the violation of Bell’s inequalities59,
for any pure state. This is reminiscent of the argument by von Neumann that the entropy of all pure states is defined to be 0 as a kind of normalization56. Finally, since the Brukner-Zeilinger invariant information was successfully utilized in quantum teleportation57, state estimation58 and the violation of Bell’s inequalities59,  , as a renormalized version of
, as a renormalized version of  , also plays an important role in all these quantum information tasks.
, also plays an important role in all these quantum information tasks.
Observation II: The coherence measure  is associated with entropy production problem of doubly-stochastic (bistochastic) quantum channels. By use of the quantum version of Kullback inequality (or a stronger Pinsker inequality60)
is associated with entropy production problem of doubly-stochastic (bistochastic) quantum channels. By use of the quantum version of Kullback inequality (or a stronger Pinsker inequality60)

Streater proved the following theorem61:
Theorem 1. Let  be a Hilbert space with dim
be a Hilbert space with dim and denote by
and denote by  the Hilbert space of operator on
the Hilbert space of operator on  with scalar product 〈A, B〉 = Tr (A†B). If
with scalar product 〈A, B〉 = Tr (A†B). If  is a bistochastic channel which is ergodic and has spectral gap γ ∈ [0, 1) (e.g., up to a scalar multiple, the identity matrix
is a bistochastic channel which is ergodic and has spectral gap γ ∈ [0, 1) (e.g., up to a scalar multiple, the identity matrix  is the only fixed point of T in
is the only fixed point of T in  and the spectrum of the channel T† ◦T is contained in the set [0, 1 − γ]∪{1}), then for any density matrix ρ
and the spectrum of the channel T† ◦T is contained in the set [0, 1 − γ]∪{1}), then for any density matrix ρ

where S(ρ) = −Tr(ρ ln ρ) is the von Neumann entropy of ρ.
From Theorem 1, we find that two separated terms contribute to the lower bound of the entropy production. The first term  is just the unnormalized version of
is just the unnormalized version of  , which characterizes the intrinsic coherence independent of the choice of a specific basis, while the spectral gap γ relies on representations of both T and ρ. To further elucidate the role of the bistochastic channel T, we consider the thermodynamics problem raised in ref. 62, where the the bistochastic channel was taken to be a projection measurement ρ → Δ(ρ) : = ∑kΠkρΠk. If {|l〉}l is the eigenbasis of ρ and {Πk = |ϕk〉〈ϕk|}k constitute another orthogonal basis, then γ is the second smallest eigenvalue of the matrix
, which characterizes the intrinsic coherence independent of the choice of a specific basis, while the spectral gap γ relies on representations of both T and ρ. To further elucidate the role of the bistochastic channel T, we consider the thermodynamics problem raised in ref. 62, where the the bistochastic channel was taken to be a projection measurement ρ → Δ(ρ) : = ∑kΠkρΠk. If {|l〉}l is the eigenbasis of ρ and {Πk = |ϕk〉〈ϕk|}k constitute another orthogonal basis, then γ is the second smallest eigenvalue of the matrix  , where M is a bistochastic matrix with the entries Mkl = 〈l|Πk|l〉 = |〈ϕk|l〉|2. It is easy to show that γ is zero if {|l〉}l and {|ϕk〉}k are the same, while γ = 1 if they are mutually unbiased. A deeper insight can be gained by noticing that once quantum thermodynamics is viewed as a resource theory, it can be cast as a hybrid of the resource theory of purity and the resource theory of asymmetry16. In particular, if {Πk}k are the eigenvectors of an observable L, γ (e.g., second smallest eigenvalue of
, where M is a bistochastic matrix with the entries Mkl = 〈l|Πk|l〉 = |〈ϕk|l〉|2. It is easy to show that γ is zero if {|l〉}l and {|ϕk〉}k are the same, while γ = 1 if they are mutually unbiased. A deeper insight can be gained by noticing that once quantum thermodynamics is viewed as a resource theory, it can be cast as a hybrid of the resource theory of purity and the resource theory of asymmetry16. In particular, if {Πk}k are the eigenvectors of an observable L, γ (e.g., second smallest eigenvalue of  ) is a quantifier to characterize to what extent ρ fails to commute with L and γ ≠ 0 if and only if ρ has some coherence over the eigenspaces of L. This line of thought coincides with that of Marvian et al.36.
) is a quantifier to characterize to what extent ρ fails to commute with L and γ ≠ 0 if and only if ρ has some coherence over the eigenspaces of L. This line of thought coincides with that of Marvian et al.36.
Observation III: For a square d-dimensional matrix A and p ∈ [1, +∞), the lp norms (or vector norms) and Schatten-p norms are defined as63

where  , r = rank(A) and
, r = rank(A) and  is used to refer to the vector of nonzero singular values
is used to refer to the vector of nonzero singular values  . In addition to the monotonicity
. In addition to the monotonicity  for 1 ≤ p ≤ q ≤ ∞, we can prove the following inequality by using Hölder’s inequality64
for 1 ≤ p ≤ q ≤ ∞, we can prove the following inequality by using Hölder’s inequality64

Note that the monotonicity and the above inequality12 is also satisfied by lp norms and the Schatten-p norms of A coincides with the ordinary (vector) lp norms of  . In particular, the Frobenius norm of A coincides with the corresponding l2 norm. Therefore,
. In particular, the Frobenius norm of A coincides with the corresponding l2 norm. Therefore,  gives a upper bound of l1 norm coherence and trace-norm coherence discussed in refs 18 and 27 respectively
gives a upper bound of l1 norm coherence and trace-norm coherence discussed in refs 18 and 27 respectively


where  denotes the set of diagonal states defined in a pre-fixed basis. It is not surprising that the upper bounds 13,14 are not tight in general though
denotes the set of diagonal states defined in a pre-fixed basis. It is not surprising that the upper bounds 13,14 are not tight in general though  and Ctr(ρ) indeed achieve their maximum values with the closest state
and Ctr(ρ) indeed achieve their maximum values with the closest state  . In fact,
. In fact,  and
and  , which is satisfied by the maximally coherent state18.
, which is satisfied by the maximally coherent state18.
On the other hand, it is intuitive to assume that the intrinsic coherence measure  may have a natural relationship with the resource theory of purity65, due to the fact that
may have a natural relationship with the resource theory of purity65, due to the fact that  is proportional to
is proportional to  . Actually,
. Actually,  provide a lower bound for the so-called unique measure of information introduced in ref. 66. By virtue of the quantum Kullback inequality9, we have
provide a lower bound for the so-called unique measure of information introduced in ref. 66. By virtue of the quantum Kullback inequality9, we have

where  is a unique measure for information, in the sense that
is a unique measure for information, in the sense that  is equal to the optimal transition rate for mixed states to one qubit pure state π (i.e., π = |0〉〈0|)16,65. However, since the Kullback inequality is not very sharp, this lower bound is rather loose, especially for the states with high purity.
is equal to the optimal transition rate for mixed states to one qubit pure state π (i.e., π = |0〉〈0|)16,65. However, since the Kullback inequality is not very sharp, this lower bound is rather loose, especially for the states with high purity.
Cohering (Purifying) power of quantum channels
With the framework of Baumgratz et al.18, we proposed the notion of cohering power of quantum channels (i.e., completely positive and trace preserving maps)23, which has been further explored in ref. 67. In the context of this work, we can introduce a similar quantity to characterize the cohering (purifying) capacity of quantum channels

Complete positivity of  enables a Kraus decomposition
enables a Kraus decomposition

where the second relation stems from the trace preserving property. Thus, the cohering power16 can be rewritten as

It is observed that the operator  is Hermitian and traceless. Moreover,
is Hermitian and traceless. Moreover,  if and only if
if and only if  is a unital quantum channel, i.e., doubly-stochastic (bistochastic) completely positive map or
is a unital quantum channel, i.e., doubly-stochastic (bistochastic) completely positive map or  68. Therefore, the cohering capacity
68. Therefore, the cohering capacity  can be recognized as a measure of nonunitality of quantum channels. Note that the nonunital channels also play a crucial role in the local creation of quantum correlations69. Within the scope of resource theories16,17, we may make a correspondence in our context: the only free state is the maximally mixed state
can be recognized as a measure of nonunitality of quantum channels. Note that the nonunital channels also play a crucial role in the local creation of quantum correlations69. Within the scope of resource theories16,17, we may make a correspondence in our context: the only free state is the maximally mixed state  , the free operations are unital channels and the resources are states with
, the free operations are unital channels and the resources are states with  . The justification of such a correspondence relies on the monotonicity of the function
. The justification of such a correspondence relies on the monotonicity of the function  under unital channels. The following theorem proves that it is the case.
under unital channels. The following theorem proves that it is the case.
Theorem 2 For any unital (i.e, bistochastic) quantum channel, it holds that  .
.
Proof. Since  , it is sufficient to prove
, it is sufficient to prove  . Consider the Kraus decomposition of
. Consider the Kraus decomposition of  and we have
and we have

where we have defined  . It is interesting to see that {Aμν} also constitute a unital quantum channel
. It is interesting to see that {Aμν} also constitute a unital quantum channel  due to the identities
due to the identities


where the unitality of  is used. With the aid of Chauchy-Schwarz inequality for operators
is used. With the aid of Chauchy-Schwarz inequality for operators  for p−1 + q−1 = 1 (e.g., p = q = 2 in our case), we finally obtain
for p−1 + q−1 = 1 (e.g., p = q = 2 in our case), we finally obtain

where the unitality property of A(⋅) is applied.
We have attempted to check whether the unitality of quantum channels is also a necessary condition for the monotonicity of  . Note that for finite-dimensional Hilbert spaces, a dynamical semigroup is strictly purity-decreasing if and only if the Lindblad generator is unital70. However, actually the Kraus or operator-sum representation is more general than the master equation approach3. Therefore, the necessity of unitality of operator-sum representation for strictly-decreasing purity is still an important unsolved problem. See Method section for more information.
. Note that for finite-dimensional Hilbert spaces, a dynamical semigroup is strictly purity-decreasing if and only if the Lindblad generator is unital70. However, actually the Kraus or operator-sum representation is more general than the master equation approach3. Therefore, the necessity of unitality of operator-sum representation for strictly-decreasing purity is still an important unsolved problem. See Method section for more information.
Asymmetry measure based on Frobenius norm
In realistic physical scenarios, there are some states which are invariant under a set of symmetric operations or a given symmetric group. This fact tells us that a specific group of symmetric transformations assigns a specific type of symmetry to the underlying systems. A state ρ is called symmetric (or G-invariant) with respect to a finite or compact Lie group G if it satisfies34,36,71

where U(g) denotes a unitary representation corresponding to the group element g ∈ G. We notice that this definition of symmetry is equivalent to other two criterions

where the summation in  will be replaced by integral over dg when a compact Lie group is considered. The criterion (i) induced a nature entropic measure of the asymmetry of ρ with respect to G36,71, (i.e.,
will be replaced by integral over dg when a compact Lie group is considered. The criterion (i) induced a nature entropic measure of the asymmetry of ρ with respect to G36,71, (i.e.,  ), which was also proved to be a measure of the quality of a quantum reference frame33. Based on the criterion (ii), it is realized that the commutator [U(g), ρ] characterizes to what extent ρ is asymmetric with respect to G and some matrix norm of [U(g), ρ] should be a reasonable measure of G-asymmetry36.
), which was also proved to be a measure of the quality of a quantum reference frame33. Based on the criterion (ii), it is realized that the commutator [U(g), ρ] characterizes to what extent ρ is asymmetric with respect to G and some matrix norm of [U(g), ρ] should be a reasonable measure of G-asymmetry36.
Along this line of thought, a new quantifier of asymmetry has recently been proposed by Sun’s group, which is defined as an average of the fidelity deviations of Hamiltonian H (or quantum state ρ) over a specific symmetric group g ∈ G46

where H0 = H − TrH/d is a re-biased version of H.  is mathematically tractable and also has desirable properties (e.g., basis-independence), mainly owing to the geometric feature of the Frobenius norm64. More importantly, it is has been demonstrated that
is mathematically tractable and also has desirable properties (e.g., basis-independence), mainly owing to the geometric feature of the Frobenius norm64. More importantly, it is has been demonstrated that  can effectively detect some significant phenomena in condensed matter physics, such as accidental degeneracy and spontaneous symmetry breaking46. Meanwhile, an analogous measure can be defined since we are more concerned with how to quantify the asymmetry (symmetry) of quantum states
can effectively detect some significant phenomena in condensed matter physics, such as accidental degeneracy and spontaneous symmetry breaking46. Meanwhile, an analogous measure can be defined since we are more concerned with how to quantify the asymmetry (symmetry) of quantum states


With this formulation, we can investigate the asymmetry of any quantum state with respect to a specific symmetric group. Remarkably, while seemingly unrelated, there actually exists a close connection between  and
and  . We first focus on the single qubit system
. We first focus on the single qubit system  , where
, where  is the Bloch vector and can be parameterized as
is the Bloch vector and can be parameterized as  with polar and azimuthal angles (θ0, ϕ0). Since the group of all linear unitary operations over a single qubit is equivalent to a
with polar and azimuthal angles (θ0, ϕ0). Since the group of all linear unitary operations over a single qubit is equivalent to a  algebra, here what interests us most is to investigate the performance of
algebra, here what interests us most is to investigate the performance of  under the
under the  group. The group element of
group. The group element of  can be expressed as
can be expressed as

where  is a real unit vector and for simplicity we denote the triple as a vector
is a real unit vector and for simplicity we denote the triple as a vector  . With the identity
. With the identity  and
and  , the quantity
, the quantity  for
for  group can be explicitly calculated
group can be explicitly calculated

where we have used the integral formula for a functional  over the
over the  group72
group72

and in our case the functional  can be represented as
can be represented as

As expected, the result29 indicates that  is a basis-independent quantity, that is, it does not rely on the initial orientation of
is a basis-independent quantity, that is, it does not rely on the initial orientation of  , although F(ω, θ, ϕ) explicitly depend on θ0 and ϕ0. Moreover, when
, although F(ω, θ, ϕ) explicitly depend on θ0 and ϕ0. Moreover, when  = 0, the initial state ρ is the maximally mixed state
= 0, the initial state ρ is the maximally mixed state  and meanwhile
and meanwhile  . This observation coincides with the fact that for any symmetry and for any representation of the symmetry, the completely mixed state
. This observation coincides with the fact that for any symmetry and for any representation of the symmetry, the completely mixed state  is invariant under all symmetry transformations34. Intriguingly, we build up a relationship between
is invariant under all symmetry transformations34. Intriguingly, we build up a relationship between  and
and  for arbitrary single-qubit system
for arbitrary single-qubit system

Apparently,  is a monotonic increasing function of
is a monotonic increasing function of  , which implies that more intrinsic coherence signifies more asymmetry under the
, which implies that more intrinsic coherence signifies more asymmetry under the  group. Such a simple but novel relation motivates us to inspect
group. Such a simple but novel relation motivates us to inspect  for N-qubit states by invoking the tensor product structure of Hilbert space.
for N-qubit states by invoking the tensor product structure of Hilbert space.
An arbitrary N-qubit (pure or mixed) states can be written as

where  (xj = 1, 2, 3) are the standard Pauli matrices in the Hilbert space of qubit j and
(xj = 1, 2, 3) are the standard Pauli matrices in the Hilbert space of qubit j and  is the corresponding identity operator. The set of real coefficients
is the corresponding identity operator. The set of real coefficients  with xj = 1, 2, 3 constitutes the so-called correlation matrix T. To gain further insight into the property of
with xj = 1, 2, 3 constitutes the so-called correlation matrix T. To gain further insight into the property of  , we consider the symmetry group
, we consider the symmetry group  , where the group element is
, where the group element is  and
and  are independent local unitary operations acting on qubit j. Similar to the single-qubit case 29, the key procedure is to calculate the average of
are independent local unitary operations acting on qubit j. Similar to the single-qubit case 29, the key procedure is to calculate the average of  over
over  . Due to the tensor product structure of N-qubit states and the trace formula Tr(A⊗B) = Tr(A)Tr(B), we have the relation
. Due to the tensor product structure of N-qubit states and the trace formula Tr(A⊗B) = Tr(A)Tr(B), we have the relation

Therefore, the problem reduces to the evaluation of the integral  . In fact, we can prove that only when xj = yj = 0, this integral is nonzero, namely (see Methods section)
. In fact, we can prove that only when xj = yj = 0, this integral is nonzero, namely (see Methods section)

Finally, we obtain the asymmetry of N-qubit states under  in a general form
in a general form

where the coefficient  . Obviously, this result reduces to the single-qubit case for N = 1 and the maximally mixed state
. Obviously, this result reduces to the single-qubit case for N = 1 and the maximally mixed state  still corresponds to the minimum value of
still corresponds to the minimum value of 
 . In addition to the unambiguous and monotonous relation between
. In addition to the unambiguous and monotonous relation between  and
and  (hence
(hence  ), it is worthwhile to note that
), it is worthwhile to note that  is independent of the correlation matrix T, more precisely, independent of the internal quantum correlations (e.g., entanglement) between subsystems.
is independent of the correlation matrix T, more precisely, independent of the internal quantum correlations (e.g., entanglement) between subsystems.
Intuitively, one might be tempted to conjecture that any local symmetric transformation group G will lead to a correlation-independent measure of asymmetry. However, this is not the case. To illustrate this, let us take a closer look at local unitary transformations. Other than the independent local unitary transformations considered above, their collective counterparts also plays a crucial role in quantum information and computation73. In this circumstance, the element of symmetry group is the tensor product of N identical unitary transformations  , that is,
, that is,  . Take two-qubit states for example and we obtain (see Methods section for more details)
. Take two-qubit states for example and we obtain (see Methods section for more details)

It is evident that the collective effect exhibits a significant influence on the asymmetry measure and  indeed relies on the diagonal entries of the correlation matrix T, which are basis-dependent quantities.
indeed relies on the diagonal entries of the correlation matrix T, which are basis-dependent quantities.
Discussion
In this work, we first formulate a coherence measure  based on the Frobenius norm, which is defined from a geometric perspective. Remarkably, we have demonstrated that this quantity is not only a measure of mixedness, but also an intrinsic (basis-independent) quantification of quantum coherence contained in quantum states, which can also be viewed as a normalized version of Brukner-Zeilinger information52. To further illustrate this point, a comparison can be made between
based on the Frobenius norm, which is defined from a geometric perspective. Remarkably, we have demonstrated that this quantity is not only a measure of mixedness, but also an intrinsic (basis-independent) quantification of quantum coherence contained in quantum states, which can also be viewed as a normalized version of Brukner-Zeilinger information52. To further illustrate this point, a comparison can be made between  and the coherence measures proposed by Baumgratz et al.18. For example, for a single-qubit state
and the coherence measures proposed by Baumgratz et al.18. For example, for a single-qubit state  , those quantifiers are listed as follows
, those quantifiers are listed as follows


where h(x) = −xlog x − (1 − x)log (1 − x) is the binary entropy function and CR(ρ) is the relative entropy of coherence. From the above expressions, it is evident that CR(ρ),  and Ctr(ρ) are all basis-dependent measures, since they all depend on s3, which is not a unitarily-invariant quantity. Moreover, the participation of s3 precisely reflects the choice of the pre-fixed basis. In fact, we can present an alternative formulation of
and Ctr(ρ) are all basis-dependent measures, since they all depend on s3, which is not a unitarily-invariant quantity. Moreover, the participation of s3 precisely reflects the choice of the pre-fixed basis. In fact, we can present an alternative formulation of  based on the eigenvalues λj of ρ, by noticing that λj − 1/d is the corresponding eigenvalues of
based on the eigenvalues λj of ρ, by noticing that λj − 1/d is the corresponding eigenvalues of  , which is a Hermitian and traceless operator
, which is a Hermitian and traceless operator

Note that  for any pure state. This result is just a consequence of the basis-dependent property of
for any pure state. This result is just a consequence of the basis-dependent property of  : pure states can only be represented as a coherent superposition in any pre-fixed basis (without including itself as a base vector) and more precisely, any pure state can always be connected by a unitary transformation within a given dimension. In contrast to quantum correlations,
: pure states can only be represented as a coherent superposition in any pre-fixed basis (without including itself as a base vector) and more precisely, any pure state can always be connected by a unitary transformation within a given dimension. In contrast to quantum correlations,  is a global property of quantum states, which quantifies the intrinsic randomness irrespective of the amount of entanglement between subsystems. This is reminiscent of the argument by von Neumann that the entropy of all pure states is defined to be zero as a kind of normalization, but the entropy itself does not give a clue on the quantum correlations between subsystems of the (pure) states. Moreover, the current construction of coherence measure is not valid for infinite dimensional systems and a possible solution is to invoke the so-called extended (or unitized) Hilbert-Schmidt algebra instead74.
is a global property of quantum states, which quantifies the intrinsic randomness irrespective of the amount of entanglement between subsystems. This is reminiscent of the argument by von Neumann that the entropy of all pure states is defined to be zero as a kind of normalization, but the entropy itself does not give a clue on the quantum correlations between subsystems of the (pure) states. Moreover, the current construction of coherence measure is not valid for infinite dimensional systems and a possible solution is to invoke the so-called extended (or unitized) Hilbert-Schmidt algebra instead74.
Analogous to previous works23,67, the cohering power  of quantum channels is introduced in our context. It is demonstrated that
of quantum channels is introduced in our context. It is demonstrated that  if and only if
if and only if  is a unital quantum channel, i.e., doubly-stochastic (bistochastic) completely positive map. Therefore, the cohering capacity
is a unital quantum channel, i.e., doubly-stochastic (bistochastic) completely positive map. Therefore, the cohering capacity  can be recognized as a measure of nonunitality of quantum channels. For instance, for some common types of decoherence processes (such as depolarizing and phase damping channels)
can be recognized as a measure of nonunitality of quantum channels. For instance, for some common types of decoherence processes (such as depolarizing and phase damping channels)  since they are unital quantum channels. However, for dissipative channels (e.g., amplitude damping channel)
since they are unital quantum channels. However, for dissipative channels (e.g., amplitude damping channel)  is exactly equal to the damping parameter γ, which can be thought of as the probability of losing a photon (here we adopt the notations in ref. 3). Intrudingly, the spontaneous emission process is one of the strongest cohering channels, due to the fact that it maps any state into a certain pure state (e.g., the ground state of a system). As a comparison, it’s worth noting that J. Wallman proposed a measure of coherence of quantum operations rather than the coherence of quantum states, where the role of purity is also highlighted75. Based on the commutator between quantum state and the elements of a specific symmetric group G, we formulate an asymmetry measure
is exactly equal to the damping parameter γ, which can be thought of as the probability of losing a photon (here we adopt the notations in ref. 3). Intrudingly, the spontaneous emission process is one of the strongest cohering channels, due to the fact that it maps any state into a certain pure state (e.g., the ground state of a system). As a comparison, it’s worth noting that J. Wallman proposed a measure of coherence of quantum operations rather than the coherence of quantum states, where the role of purity is also highlighted75. Based on the commutator between quantum state and the elements of a specific symmetric group G, we formulate an asymmetry measure  by integrating the Frobenius norm of the commutator over this group. Two distinct situations are considered: local independent and collective
by integrating the Frobenius norm of the commutator over this group. Two distinct situations are considered: local independent and collective  transformations. For N-qubit quantum states,
transformations. For N-qubit quantum states,  only relies on the purity and is actually equivalent to
only relies on the purity and is actually equivalent to  (or
(or  ) under local independent
) under local independent  transformations. However, for local collective
transformations. However, for local collective  transformations,
transformations,  also depends on the quantum correlations between subsystems. One important open question is to find a closed expression of
also depends on the quantum correlations between subsystems. One important open question is to find a closed expression of  for arbitrary N-qubit states (especially N > 3) in this case.
for arbitrary N-qubit states (especially N > 3) in this case.
Methods
Normalization of  and
and 
Here we only focus on  , because
, because  is a completely positive and trace preserving map and hence
is a completely positive and trace preserving map and hence  is also a valid density matrix. Trace-preserving property renders
is also a valid density matrix. Trace-preserving property renders  and we obtain
and we obtain

Note that for p ∈ [1, +∞) and an arbitrary non-negative vector  , the following inequality holds for vector p-norms76
, the following inequality holds for vector p-norms76

Since the Schatten-p norms of an operator A is equal to its vector p-norm of its singular values (e.g.,  ), the above inequality also holds for Schatten-p norms. Therefore, we have
), the above inequality also holds for Schatten-p norms. Therefore, we have

where we have used  due to the positivity of
due to the positivity of  and the monotonicity
and the monotonicity  . It is quite clear that the equality is satisfied only if the quantum channel
. It is quite clear that the equality is satisfied only if the quantum channel  maps the maximally mixed state
maps the maximally mixed state  to a pure state, which only possesses intrinsic (e.g., basis-independent) coherence in our context.
to a pure state, which only possesses intrinsic (e.g., basis-independent) coherence in our context.
Necessity of unital channels
In ref. 70, it is proved that a dynamical semigroup is strictly purity-decreasing if and only if the Lindblad generator is unital. Here the quantum dynamic semigroup (in the Schrödinger picture) is a family of one-parameter linear trace-preserving maps  satisfying an additional property except for complete positivity, namely77
satisfying an additional property except for complete positivity, namely77

which is called semigroup condition or Markov property. However, we recall that a linear map  is completely positive if and only if it admits a Kraus representation. Thus in our context we are dealing with a more general class of dynamical maps. Note that Nielsen and Chuang stated in their book that a quantum process described in terms of an operator-sum representation cannot necessarily be written down as a master equation, especially for non-Markovian dynamics3. In particular, it is worth pointing out that the technique used in ref. 70 does not work for our purpose. Therefore, the necessity of unitality of operator-sum representation for strictly-decreasing purity is still an important unsolved problem.
is completely positive if and only if it admits a Kraus representation. Thus in our context we are dealing with a more general class of dynamical maps. Note that Nielsen and Chuang stated in their book that a quantum process described in terms of an operator-sum representation cannot necessarily be written down as a master equation, especially for non-Markovian dynamics3. In particular, it is worth pointing out that the technique used in ref. 70 does not work for our purpose. Therefore, the necessity of unitality of operator-sum representation for strictly-decreasing purity is still an important unsolved problem.
Moreover, though we present an elegant proof of the sufficient part, we can reach this conclusion from a different perspective. For α ∈ (0, 1)∪(1, +∞), the quantum α-divergence28

where we assume that supp(ρ)⊂supp(σ). The monotonicity of  under unital channels follows from the facts that
under unital channels follows from the facts that  is monotone under completely positive and trace preserving maps in the range α ∈ (0, 2]28 and
is monotone under completely positive and trace preserving maps in the range α ∈ (0, 2]28 and  .
.
Integrals over independent and collective local unitary transformations
For independent local unitary transformations, the key task is to calculate the integral  . For simplicity, we define
. For simplicity, we define  . A straightforward observation shows that the evaluations of
. A straightforward observation shows that the evaluations of  can be divided into four categories
can be divided into four categories

The first three situations are evident but the last one is not immediately obvious. In order to calculate  , the key point is that for any σj (j = 1, 2, 3), one can always find an operator
, the key point is that for any σj (j = 1, 2, 3), one can always find an operator  such that UσjU† = σ3. Moreover, this operator can be absorbed into the average over
such that UσjU† = σ3. Moreover, this operator can be absorbed into the average over  . Therefore, we only need to consider
. Therefore, we only need to consider  . Finally, we can obtain
. Finally, we can obtain

where we have used the identity

and the commutation relations

Finally, for any i, j = 1, 2, 3 we have

However, the situation is much more complex when confronted with the collective local unitary transformations. Take two-qubit state for example and in this case we should deal with the integral  . Similar analysis leads to the fact
. Similar analysis leads to the fact

Special attention should be paid to the case x1 = x2 ≠ 0, y1 = y2 ≠ 0, that is

We have also considered the three-qubit state and only present the result here

where δi,j and εi,j,k denote the Kronecker delta and Levi-Civita symbol, respectively. However, the generalization to arbitrary N-qubit states is still missing, which is left as an open question for further study.
Additional Information
How to cite this article: Yao, Y. et al. Frobenius-norm-based measures of quantum coherence and asymmetry. Sci. Rep. 6, 32010; doi: 10.1038/srep32010 (2016).
References
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145 (2002).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222 (2011).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Communication (Cambridge University Press, Cambridge, 2000).
Schrödinger, E. Discussion of Probability Relations between Separated Systems. Math. Proc. Cambridge Philos. Soc. 31, 555 (1935).
Glauber, R. J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 131, 2766 (1963).
Sudarshan, E. C. G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 10, 277 (1963).
Mandel, L. & Wolf, E. Optical Coherence and Quantum Optics (Cambridge University Press, Cambridge, England, 1995).
Born, M. & Wolf, E. Principles of Optics (Cambridge Univ. Press, 1999).
Wolf, E. Introduction to the Theory of Coherence and Polarization of Light (Cambridge Univ. Press, 2007).
Karczewski, B. Degree of coherence of the electromagnetic field. Phys. Lett. 5, 191–192 (1963).
Wolf, E. Unified theory of coherence and polarization of random electromagnetic fields. Phys. Lett. A 312, 263–267 (2003).
Tervo, J., Setälä, T. & Friberg, A. T. Degree of coherence for electromagnetic fields. Opt. Express 11, 1137–1143 (2003).
Setälä, T., Tervo, J. & Friberg, A. T. Complete electromagnetic coherence in the space-frequency domain. Opt. Lett. 29, 328–330 (2004).
Wolf, E. Comment on ‘Complete electromagnetic coherence in the space-frequency domain’. Opt. Lett. 29, 1712 (2004).
Setälä, T., Tervo, J. & Friberg, A. T. Reply to comment on ‘Complete electromagnetic coherence in the space-frequency domain’. Opt. Lett. 29, 1713–1714 (2004).
Horodecki, M. & Oppenheim, J. (Quantumness in the context of) resource theories. Int. J. Mod. Phys. B 27, 1345019 (2013).
Brandão, F. G. S. L. & Gour, G. Reversible Framework for Quantum Resource Theories. Phys. Rev. Lett. 115, 070503 (2015).
Baumgratz, T., Cramer, M. & Plenio, M. B. Quantifying Coherence. Phys. Rev. Lett. 113, 140401 (2014).
Vedral, V., Plenio, M. B., Rippin, M. A. & Knight, P. L. Quantifying Entanglement. Phys. Rev. Lett. 78, 2275 (1997).
Girolami, D. Observable Measure of Quantum Coherence in Finite Dimensional Systems. Phys. Rev. Lett. 113, 170401 (2014).
Shao, L.-H., Xi, Z., Fan, H. & Li, Y. Fidelity and trace-norm distances for quantifying coherence. Phys. Rev. A 91, 042120 (2015).
Streltsov, A., Singh, U., Dhar, H. S., Bera, M. N. & Adesso, G. Measuring Quantum Coherence with Entanglement. Phys. Rev. Lett. 115, 020403 (2015).
Yao, Y., Xiao, X., Ge, L. & Sun, C. P. Quantum coherence in multipartite systems. Phys. Rev. A 92, 022112 (2015).
Yuan, X., Zhou, H., Cao, Z. & Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 92, 022124 (2015).
Xi, Z., Li, Y. & Fan, H. Quantum coherence and correlations in quantum system. Sci. Rep. 5, 10922 (2015).
Cheng, S. & Hall, M. J. W. Complementarity relations for quantum coherence. Phys. Rev. A 92, 042101 (2015).
Rana, S., Parashar, P. & Lewenstein M. Trace-distance measure of coherence. Phys. Rev. A 93, 012110 (2015).
Rastegin, A. E. Quantum-coherence quantifiers based on the Tsallis relative α entropies. Phys. Rev. A 93, 032136 (2016).
Napoli, C. et al. Robustness of coherence: An operational and observable measure of quantum coherence. Phys. Rev. Lett. 116, 150502 (2016).
Chitambar, E. et al. Assisted Distillation of Quantum Coherence. Phys. Rev. Lett. 116, 070402 (2016).
Winter, A. & Yang D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 116, 120404 (2016).
Gour, G. & Spekkens, R. W. The resource theory of quantum reference frames: manipulations and monotones. New J. Phys. 10, 033023 (2008).
Gour, G., Marvian, I. & Spekkens, R. W. Measuring the quality of a quantum reference frame: The relative entropy of frameness. Phys. Rev. A 80, 012307 (2009).
Marvian, I. & Spekkens, R. W. The theory of manipulations of pure state asymmetry: I. Basic tools, equivalence classes and single copy transformations. New J. Phys. 15, 033001 (2013).
Marvian, I. & Spekkens, R. W. Modes of asymmetry: The application of harmonic analysis to symmetric quantum dynamics and quantum reference frames. Phys. Rev. A 90, 062110 (2014)
Marvian, I. & Spekkens, R. W. Extending Noether’s theorem by quantifying the asymmetry of quantum states Nat. Commun. 5, 3821 (2014).
Marvian, I., Spekkens, R. W. & Zanardi, P. Quantum speed limits, coherence and asymmetry. arXiv:1510.06474.
Marvian, I. & Spekkens, R. W. How to quantify coherence: distinguishing speakable and unspeakable notions. arXiv:1602.08049.
Chitambar, E. & Gour, G. Are Incoherent Operations Physically Consistent?—A Critical Examination of Incoherent Operations. arXiv:1602.06969.
Singh, U., Bera, M. N., Misra, A. & Pati, A. K. Erasing Quantum Coherence: An Operational Approach. arXiv:1506.08186.
Bagan, E., Bergou, J. A., Cottrell, S. S. & Hillery M. Relations between coherence and path information. Phys. Rev. Lett. 116, 160406 (2016).
Singh, U., Bera, M. N., Dhar, H. S. & Pati, A. K. Maximally coherent mixed states: Complementarity between maximal coherence and mixedness. Phys. Rev. A 91, 052115 (2015).
Bera, M. N., Qureshi, T., Siddiqui, M. A. & Pati, A. K. Duality of quantum coherence and path distinguishability. Phys. Rev. A 92, 012118 (2015).
Kagalwala, K. H., Giuseppe, G. D., Abouraddy, A. F. & Saleh, B. E. Bell’s measure in classical optical coherence. Nat. Photonics 7, 72 (2013).
Svozilík, J., Vallés, A., Peřina, J. J. & Torres, J. P. Revealing Hidden Coherence in Partially Coherent Light. Phys. Rev. Lett. 115, 220501 (2015).
Fang, Y. N., Dong, G. H., Zhou, D. L. & Sun, C. P. Quantification of Symmetry. Commun. Theor. Phys. 65, 423–433 (2016).
Setälä, T., Kaivola, M. & Friberg, A. T. Degree of Polarization in Near Fields of Thermal Sources: Effects of Surface Waves. Phys. Rev. Lett. 88, 123902 (2002).
Setälä, T., Shevchenko, A., T., Kaivola, M. & Friberg, A. T. Degree of polarization for optical near fields. Phys. Rev. E 66, 016615 (2002).
Luis, A. Degree of coherence for vectorial electromagnetic fields as the distance between correlation matrices. J. Opt. Soc. Am. A 24, 1063–1068 (2007).
Gil, J. J. & Bernabeu, E. Depolarization and polarization indices of an optical system. Opt. Acta 33, 185–189 (1986).
Aiello, A. & Woerdman, J. P. Physical bounds to the entropy-depolarization relation in random light scattering. Phys. Rev. Lett. 94, 090406 (2005).
Brukner, C. & Zeilinger, A. Operationally Invariant Information in Quantum Measurements. Phys. Rev. Lett. 83, 3354 (1999).
Brukner, C. & Zeilinger, A. Conceptual inadequacy of the Shannon information in quantum measurements. Phys. Rev. A 63, 022113 (2001).
Munro, W. J., James, D. F. V., White, A. G. & Kwiat, P. G. Maximizing the entanglement of two mixed qubits. Phys. Rev. A 64, 030302 (2001).
Wei, T.-C., Nemoto, K., Goldbart, P. M., Kwiat, P. G., Munro, W. J. & Verstraete, F. Maximal entanglement versus entropy for mixed quantum states. Phys. Rev. A 67, 022110 (2003).
Neumann, J. V. Mathematical Foundations of Quantum Mechanics (Springer, New York, 1932).
Lee, J. & Kim, M. S. Entanglement Teleportation via Werner States. Phys. Rev. Lett. 84, 4236 (2000).
Rehacek, J. & Hradil, Z. Invariant Information and Quantum State Estimation. Phys. Rev. Lett. 88, 130401 (2002).
Brukner, C., Zukowski, M. & Zeilinger, A. The essence of entanglement. arXiv:quant-ph/0106119.
Hiai, F., Ohya, M. & Tsukada, M. Sufficiency, KMS condition and relative entropy in von Neumann algebras. Pacific J. Math. 96, 99–109 (1981).
Streater, R. F. Convergence of the quantum Boltzmann map. Comm. Math. Phys. 98, 177–185 (1985).
Kammerlander, P. & Anders, J. Coherence and measurement in quantum thermodynamics. Sci. Rep. 6, 22174 (2016).
Watrous, J. Theory of Quantum Information (University of Waterloo, Waterloo, 2011).
Bhatia, R. Matrix Analysis (Springer, 1997).
Horodecki, M., Horodecki, P. & Oppenheim, J. Reversible transformations from pure to mixed states and the unique measure of information. Phys. Rev. A 67, 062104 (2003).
Horodecki, M. et al. Local Information as a Resource in Distributed Quantum Systems. Phys. Rev. Lett. 90, 100402 (2002).
Mani, A. & Karimipour, V. Cohering and decohering power of quantum channels. Phys. Rev. A 92, 032331 (2015).
Mendl, C. B. & Wolf, M. Unital Quantum Channels–Convex Structure and Revivals of Birkhoff’s Theorem. Commun. Math. Phys. 289, 1057–1086 (2009).
Streltsov, A., Kampermann, H. & Bruss, D. Behavior of Quantum Correlations under Local Noise. Phys. Rev. Lett. 107, 170502 (2011).
Lidar, D. A., Shabani, A. & Alicki, R. Conditions for strictly purity-decreasing quantum Markovian dynamics. Chem. Phys. 322, 82–86 (2006).
Vaccaro, J. A., Anselmi, F., Wiseman, H. M. & Jacobs, K. Tradeoff between extractable mechanical work, accessible entanglement and ability to act as a reference system, under arbitrary superselection rules. Phys. Rev. A 77, 032114 (2008).
Gilmore, R. Lie Groups, Lie Algebras and Some of Their Applications (Wiley, New York, 1974).
Bourennane, M. et al. Decoherence-free quantum information processing with four-photon entangled states. Phys. Rev. Lett. 92, 107901 (2004).
Minh, H., Biagio, M. & Murino, V. Log-Hilbert-Schmidt metric between positive definite operators on Hilbert spaces. In: Advances in Neural Information Processing Systems 27 (NIPS), pp. 388–396 (2014).
Wallman, J., Granade, C., Harper, R. & Flammia, S. T. Estimating the coherence of noise. New J. Phys. 17, 113020 (2015).
Roga, W., Puchała, Z., Rudnicki, Ł. & Życzkowski, K. Entropic trade-off relations for quantum operations. Phys. Rev. A 87, 032308 (2013).
Alicki, R. & Lendi, K. Quantum Dynamical Semigroups and Applications (Springer, Berlin, 2007).
Acknowledgements
This research is supported by the National Natural Science Foundation of China under Grants No. 11421063 and No. 11534002, the National Basic Research Program of China under Grants No. 2012CB922104 and No. 2014CB921403.
Author information
Authors and Affiliations
Contributions
Y.Y. and G.H.D. initiated the research project and established the main results under the guidance of C.P.S. and X.X. joined discussions and provided constructive suggestions. Y.Y. wrote the manuscript and all authors commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yao, Y., Dong, G., Xiao, X. et al. Frobenius-norm-based measures of quantum coherence and asymmetry. Sci Rep 6, 32010 (2016). https://doi.org/10.1038/srep32010
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep32010
This article is cited by
-
Characterizing nonclassical correlations of tensorizing states in a bilocal scenario
Quantum Information Processing (2023)
-
Correlation-induced coherence and its use in detecting quantum phase transitions
Science China Physics, Mechanics & Astronomy (2022)
-
Quantum coherence and its distribution in the extended Ising chain
Quantum Information Processing (2021)
-
Asymmetry-induced nonclassical correlation
Quantum Information Processing (2021)
-
Coherence and entanglement under three-qubit cloning operations
Quantum Information Processing (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

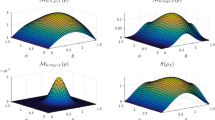
 , which is in sharp contrast to the coherence measures proposed in ref.
, which is in sharp contrast to the coherence measures proposed in ref.  is independent of the specific representation of ρ, that is,
is independent of the specific representation of ρ, that is,  is basis-independent.
is basis-independent. is unitarily invariant, since
is unitarily invariant, since  owing to the fact that the maximally mixed state
owing to the fact that the maximally mixed state  is the only state that remains invariant under arbitrary unitary transformation. In fact, the property (iv) is equivalent to (iii).
is the only state that remains invariant under arbitrary unitary transformation. In fact, the property (iv) is equivalent to (iii). has an analytical expression and explicit geometrical interpretation. As we shall see below,
has an analytical expression and explicit geometrical interpretation. As we shall see below,  also has a clear operational meaning.
also has a clear operational meaning. and
and 