Introduction

In recent years, the study of networks associated with complex systems has received the attention of researchers from many different areas. Especially, weighted networks1,2 represent the natural framework to describe natural, social, and technological systems3. The deterministic weighted networks have attracted increasing attentions because many network characteristics are exactly solved through their quantities, such as mean weighted first-passage time, average weighted shortest path4 etc.

Several recent works have studied the mean first-passage time (MFPT) for some self-similar weighted network models. Dai et al.5 found that the weighted Koch networks are more efficient than classic Koch networks in receiving information when a walker chooses one of its nearest neighbors with probability proportional to the weight of edge linking them (weight-dependent walk). Then Dai et al.6 introduced non-homogenous weighted Koch networks, and defined the mean weighted first-passage time (MWFPT) inspired by the definition of the average weighted shortest path. Sun et al.4 discussed a family of weighted hierarchical networks which are recursively defined from an initial uncompleted graph. Zhu et al.7 reported a weighted hierarchical network generated on the basis of self-similarity, and calculated analytically the expression of the MFPTs with weight-dependent walk by using a recursion relation of the hierarchical network structure. Sun et al.8 obtained the exact scalings of the mean first-passage time (MFPT) with random walks on a family of small-world treelike networks.

For un-weighted networks, calculating the entire mean first-passage time (EMFPT) generally use three methods, i.e., the definition of the EMFPT8,9, the average shortest path10, and Laplacian spectra11,12. Sun et al.8 used the definition of the EMFPT for the considered networks to obtain the analytical expressions of the EMFPT and avoided the calculations of the Laplacian spectra.

In this paper, there are two methods to calculate the entire mean weighted first-passage time (EMWFPT), 〈F〉n, for the weighted treelike networks as follows. Method 1 is to get the asymptotic behavior of the EMWFPT directly by the definition of the EMWFPT. Method 2 is to get the asymptotic behavior of the EMWFPT based on the relationship between 〈F〉n and λn, i.e, 〈F〉n = (Nn − 1)λn, where Nn is the total number of nodes. The obtained consistent results show that Method 2 is entirely feasible. Thus the effective resistance mean exactly the weight between two adjacency nodes for the weighted treelike networks. Our key finding is profound, which can help us to compute the EMWFPT by the weighted Laplacian spectra.

The organization of this paper is as follows. In next section we introduce a family of weighted treelike networks. Then we give the definition of the EMWFPT and use two methods to calculate it. In the last section we draw conclusions.

Weighted treelike networks

Recently, there are several literatures on the preferential-attachment (scale-free) method of generating a random by adding a very specific way of generating weights1,13,14. Based on Barabasi-Albert model, deterministic networks have attracted increasing attention because they have an advantage with precise formulations on some attributes. In this section a family of weighted treelike networks are introduced15,16,17, which are constructed in a deterministic iterative way. The recursive weighted treelike networks are constructed as follows.

Let r(0 < r < 1) be a positive real numbers, and s(s > 1) be a positive integer.

(1) Let G0 be base graph, with its attaching node a0 and the other nodes . Each node of links the attaching node a0 with unitary weight. We also call the attaching node a0 as the central node.

(2) For any n ≥ 1, Gn is obtained from Gn−1: Gn has one attaching node labelled by an, that we call an as the central node of Gn. Let be s copies of Gn−1, whose weighted edges have been scaled by a weight factor r. For , let us denote by the node in image of , then link all those to the attaching node .. through edges of unitary weight. Let Gn = G(Vn, En) be its associated weighted treelike network, with vertex set Vn(|Vn| = Nn) and edge set En(|En| = Nn − 1). Similarly, , . 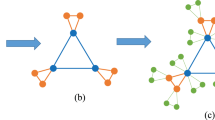In Fig. 1, we schematically illustrate the process of the first three iterations.

Figure 1: Take the ‘Sierpinski’ weighted treelike networks Gn, for example, Gn is regarded as merging , , and central Node an, n = 0, 1, 2.
figure 1

Full size image

The weighted treelike networks are set up.

According to the construction method of Gn (n ≥ 1), Gn can be regarded as merging s + 1 groups, sequentially denoted by . (see Fig. 1).

From the construction of the weighted treelike networks, one can see that Gn, the weighted treelike networks of n-th generation, is characterized by three parameters n, s and r: n being the number of generations, s being the number of copies, and r representing the weight factor. The total number of nodes Nn in Gn satisfy the following relationship, i.e. . Then

The entire mean weighted first-passing time

Assuming that the walker, at each step, starting from its current node, moves uniformly to any of its nearest neighbors. For two adjacency nodes i and j, the weighted time is defined as the corresponding edge weight wij. The mean weighted first-passing time (MWFPT) is the expected first arriving weighted time for the walks starting from a source node to a given target node. Let the source node be i and the given target node be j, denote Fij(n) by the MWFPT for a walker starting from node i to node j. We consider here the entire mean weighted first-passage time 〈F〉n as the average of Fij(n) over all pair of vertices,

To calculate the asymptotic behavior of the 〈F〉n for this model, we focus on the two methods, the definition of the EMWFPT and the average shortest path, respectively.

Method 1

In this section, we compute the EMWFPT using the definition of the EMWFPT. Step 1, we study the first quantity Qtot(n), i.e, the sum of MWFPTs for all nodes in to absorption at the central node an. Step 2, we study the second quantity Htot(n), i.e, the sum of MWFPTs for central node an to arrive all nodes in of Gn. Step 3, we use the definition to obtain the asymptotic behavior of the MWFPT between all node pairs and the asymptotic behavior of the EMWFPT in the limited of large n.

Step 1

We study the first quantity Qtot(n), i.e, the sum of MWFPTs for all nodes in to absorption at the central node an. Defining be the MWFPT of a walker from node i to the central node an for the first time. We denote by Ttot(n) the sum of MWFPTS for all nodes of Gn to absorption at the central node an.

We have already arrived the result about Ttot(n)15, i.e.

where be the MWFPT from Node to the central node an. Thus, the problem of determining Ttot(n) is reduced to finding . Note that the degree of the node is s + 1, we obtain

Through the reduction of Eq. (3), we obtain

With the initial condition of , Eq. (4) is inductively solved as

Inserting and Eq. (5) into Eq. (2), we obtain the exact solution of MWFPT from all other nodes to the central node on the networks Gn as follow

Then,

From the definition of Ttot(n), Ttot(n) is given by

where . Recalling that Eq. (1), the asymptotic behavior of Qtot(n) in the limited of large n is as follows,

Step 2

We study the second quantity Htot(n), i.e, the sum of MWFPTs for central node an to arrive all nodes in of Gn. Firstly, let Ri(n) denote the expected weighted time for a walker in weighted networks Gn, originating from node i to return to the starting point i for the first time, named mean weighted return time. By definition of , we obtain

where is the set of neighbors of the central node an and . Using Eq. (5) and Eq. (9) is solved as

Note that the degree of the node an is s, we obtain

Similarly,

Inserting Eq. (12) into Eq. (11), we obtain

From the definition of Htot(n), Htot(n) is written by

Recalling Eq. (1) and Eq. (13), Eq. (14) is solved as

The asymptotic behavior of Htot(n) in the limited of large n is as follows,

Step 3

We use the definition to obtain the asymptotic behavior of the EMWFPT in the limited of large n. Starting from the definition of the EMWFPT and the recursive construction, we can decompose the Ftot(n) into four terms:

The first term takes into account a walker starting from and arriving at nodes belonging to the same subgraph. The second term takes into account all the possible paths where the initial point and the final one belong to two different subgraphs, and we can set them to and and multiply the contribution by a combinatorial factor s(s − 1). Finally the last two terms takes into account all the possible paths between each of nodes of subgraph and the central node an.

Using the scaling mechanism for the edges, the first term in Eq. (17) can be easily identified with

By construction, each pass connecting two nodes belonging to two different subgraphs, must pass through the central node an, hence using , the second term of Eq. (17) can be split into two parts:

Then, Eq. (17) can be simplified as

Inserting Eq. (8) and Eq. (16) into Eq. (20), the asymptotic behavior of Ftot(n) in the limited of large n is as follows,

and

Method 2

In this section, Method 2 is that the average weighted shortest path used to get the asymptotic behavior the EMWFPT. This method gives some significantly new insights more straightforward than Method 1.

The resistance distance rij between two nodes i and j is defined as the effective (electrical) resistance between them when each weighted edge has been replaced by a resistor. It is known that the weighted first-passage time between two nodes is related to their resistance distance by 18,19 and, in which is the total number of edges for weighted treelike network Gn and Fi,j = Fj,i. The EMWFPT of weighted treelike network is

Let λij as the weighted shortest path between two nodes i and j of the weighted networks Gn2. For any weighted treelike networks, the weighted shortest path λij of Gn is equal to the effective resistance rij between node i and j, i.e, rij = λij. By definition the average weighted shortest path λn of the graph Gn is given by4

For a large system, i.e., Nn → ∞, we have already known that the λn of the Gn is (see ref. 17).

Now we substitute Eq. (24) and Eq. (25) into Eq. (23) obtaining,

This result coincides with the asymptotic behavior 〈F〉n in Eq. (22). Therefore, we can draw the conclusion that the effective resistance mean exactly the weight between two adjacency nodes for the weighted treelike networks.

Conclusions

In this paper, we have proposed a family of weighted treelike networks formed by three parameters as a generalization of the un-weighted trees. We have calculated the entire mean weighted first-passage time (EMWFPT) with random walks on a family of weighted treelike networks. We have used two methods to obtain the asymptotic behavior of the EMWFPT with regard to network parameters. Firstly, using the construction algorithm, we have calculated the receiving and sending times from the central nodes to the other nodes of to obtain the asymptotic behavior of the EMWFPT. Secondly, applying the relationship equation between EMWFPT and the average weighted shortest path, we also have obtained the asymptotic behavior of the EMWFPT. The dominating terms of the EMWFPT obtained by two methods are coincident, which shows that the effective resistance is equal to the weight between two adjacency nodes. Noticed that the dominating term of the EMWFPT scales linearly with network size Nn in large network. It is expected that the edge-weighted adjacency matrices can be used to compute the weighted Laplacian spectra to obtain the asymptotic behavior of the EMWFPT of weighted treelike networks.

Additional Information

How to cite this article: Dai, M. et al. The entire mean weighted first-passage time on a family of weighted treelike networks. Sci. Rep. 6, 28733; doi: 10.1038/srep28733 (2016).