Matrix description of the complete topology of three-dimensional cells

Abstract

A new, efficient method based on a series of matrices is introduced to completely describe the detailed topology of individual domains and their topology evolution in three-dimensional cellular structures. With this approach, we found a lot of new topological grain forms which are never reported before, i.e., there are total 8 and 32 topological forms for 7- and 8-faced grains respectively, other than the reported 7 and 27. This method is proved to be a practical tool to predict all possible grain forms efficiently. Moreover, a connectivity index of grain forms serves as a new convenient differentiator of different multicellular structures.

Introduction

Metals and ceramics commonly consist of space-filling arrays of single-crystal grains separated by a network of grain boundaries and foams (froths) are networks of gas-filled bubbles separated by liquid walls. Cellular structures or tessellations also occur in biological tissue and in magnetic, ferroelectric and complex fluid contexts¹.

Since the coarsening of cellular structures depends strongly on topology, the topological features of individual domains including grains, bubbles, cells, etc. in multicellular microstructures are subjects of longstanding interest which despite intensive studies is still not fully understood^{1,2,3,4,5,6,7,8,9,10}. The most widespread notion relating to grain topology is the number of grain faces^3,4,5,6,7,8. However, the number of faces of a grain is only a basic topological descriptor, it is clearly incomplete^9,10. A more detailed topology of a grain should include the information of the number of faces, edges and vertices, as well as the adjacency relationships between each feature². Of particular interest is how to describe such refined topology of grains completely and efficiently, with the ultimate object of throwing light on grain growth.

Nowadays, there are mainly two represent methods to describe the refined grain topology. Matzke⁹ introduced a more detailed topological description for bubbles in soap foams. Matzke characterized a large population of bubbles by recording the total number of faces and the number of edges of each face in each bubble. By extending this method, E.A. Lazar et al.¹⁰ introduced Weinberg vectors¹¹ and p vectors¹² to describe the grain topology and investigated the topological difference between Poisson-Voronoi and grain growth microstructures. Another method is the Schlegel diagram description of grains. Recently, B.R. Patterson et al.¹³ use Schlegel diagrams¹⁴ to describe the details of the topological flow of grains and generate some possible forms for grains with 4–9 faces.

The Schlegel diagrams of some grains, although not many in the system, are 2-connected but not 3-connected planar graphs^13,15. The Weinberg vectors description is only suitable for grains with Schlegel diagrams being 3-connected planar graphs¹⁰, while not suitable for grains with Schlegel diagrams being 2-connected planar graphs. Moreover, it is difficult to generate the large number of possible grain forms efficiently by the Schlegel description of grain form evolution in grain growth, especially for grains with large face number. It is necessary to develop a general, efficient method to describe the refined grain topology which can overcome these disadvantages of the above two methods.

In this paper, based on spectral graph theory¹⁶, we develop a new, efficient method to completely classify the topology of three-dimensional grains and apply it in the study of the topological grain forms. It involves using a series of matrices to describe the grain topology and using matrices operation to describe the grain form evolution in grain growth. With the aid of this method, we find that there are total 8 possible forms in 7-faced grain class, 32 forms in 8-faced grain class and 131 forms in 9-faced grain class respectively (See details in the Supplemental Material), which proved that a lot of grain forms are left out in the previous findings¹³.

Methods

We consider n to be the faces number of a grain, p the vertices number and q the edges number. Euler’s Law relates the faces, edges and vertices of a polyhedron as (n − q + p = 2)¹⁷. Under the restrictions of surface tension in three-dimensional cellular structures, three boundary interfaces meet at an edge and four edges meet at a vertex. Thus, for an individual grain, each edge has two vertices and each vertex radiates three edges, we can get (2q = 3p)³. We define the grain topological face adjacency matrix as the matrixA^f(e) = [α_ij]_n × n, in which α_ij = k if the face i and j have k joint edges and α_ij = 0 if i and j have no joint edge or i = j. Figure 1 shows the Schlegel diagram of a 5-faced grain and its face adjacency matrix.

Figure 1

Schlegel diagram of a 5-faced grain and its face adjacency matrix.

Topological properties like the number of grain faces, the number of edges per face and the neighboring relations among different faces are involved in this matrix and can be calculated efficiently from matrix operation. The face adjacency matrix contains all the information of the correlations among grain faces, which can be used to completely describe the grain topology. We can also define the vertex adjacency matrix and edge adjacency matrix, however, they are not the complete topology description for grains whose Schlegel diagrams are not 3-connected graph.

The grains with same topological forms have isomorphic Schlegel diagram and permutation-similar A^f(e). The spectra (i.e. the set of eigenvalues together with their multiplicities) of their A^f(e) are identical. In spectral graph theory, the (adjacency) spectrum of a graph, which is the spectrum of its adjacency matrix, is one of its topological invariants¹⁶. Thus, the spectrum of A^f(e) can be used to describe the grain topology.

The Laplacian matrix of a graph is defined as the degree matrix minus the adjacency matrix. For grain forms, the face Laplacian matrix L^f(e) = diag(d(f_i)) − A^f(e), where diag(d(f_i)) is a diagonal matrix in which the entries on main diagonal equal to the edge number of the grain faces. The second-smallest eigenvalue of the Laplacian matrix, λ₂, is a very important parameter to describe the graph characteristics, which is a topological index and called algebraic connectivity¹⁶.

Results and Discussions

Topology characteristics of grain forms

Lazar¹⁰ presented eight most common grain topologies in grain growth and Poisson-Voronoi microstructure and observed that grain growth microstructure favor certain highly symmetric grain topologies relative to the Poisson-Voronoi microstructure. Table 1. listed their corresponding λ₂ values. It can be seen that the most frequent grain forms in grain growth microstructure always has large λ₂ values among all possible forms in a given face class. For 7-, 8-, 9- and 10-faced grains in grain growth microstructures, the most frequent grain topologies corresponds to 1^st, 2^nd,1^st and 1^st largest λ₂ values in their total 8, 32, 131 and 723 forms, respectively. This reveals that some properties related to large λ₂ are favored by grain growth, termed as algebraic connectivity preferred tendency (large λ₂ preferred), besides the highly symmetric form preferred tendency observed in Lazar’s study¹⁰.

Table 1 The eight most common grain topologies in a descending order in the Poisson-Voronoi and grain growth microstructures¹⁰.

In spectral graph theory, large value of λ₂ represents good connectivity, expansion and randomness properties of a graph¹⁶. Apparently, λ₂ is influenced by not only the topological symmetry but also the edge distribution of grain faces, etc. For highly symmetric topological forms, if they have a narrow edge distribution of faces, i.e., the number of edges of each face approximates the average edges per face, the values of λ₂ are large.

Actually, a narrow edge distribution of faces for a topological form is favorable in grain growth. Grain growth involves the form transition from higher face class to lower one by the disappearing of triangular faces. If a grain has more triangular faces, it increased the probability of face loss and transfer down the topological ladder to a disappearing tetrahedron to maintain grain growth¹³. And if a grain has no triangular face, it should employ edge-switch transitions to create triangular faces before decreasing to lower face classes. For a larger-edged face, the process of transferring down its edges ladder to ultimately a triangular face is complex relative to the smaller-edged faces. From the view of edge evolution, a larger-edged face of a grain is more stable than a smaller-edged faces. On the other hand, if one of grain faces increases its stability by increasing its edges, the edges of other faces are sure to decrease under the constraint of Euler’s equation. Therefore, the realistic way to increase the stability of a topological form is to modulate the edges of each face to approximate the average edges per grain face, which result in a narrow edge distribution of faces and a large λ₂ value.

To make more clear of the difference between the algebraic connectivity and symmetry of topological forms, Fig. 2 lists all the topological forms of 7-faced grains together with the λ₂ values and the order S of the symmetry forms. The λ₂ value of each form decreased from left to right. The grain with p vector (0005200) has five 4-edged faces and two 5-edged faces, approximating to the average edges per face 4.2 for 7-faced grain class, has the largest λ₂ value 3.382. The right-hand three forms have the smallest λ₂ values, however, they have good symmetry, especially the most right hand one. These three forms are unstable and likely occur only as a transient state in the grain growth process, although they have high symmetry.

Figure 2

All eight 7-faced grain forms.

With the increase of triangular faces, the deviation degree from the average edges per face will increase, which resulted in low algebraic connectivity for grains. From the algebraic connectivity preferred tendency, these forms will have a less frequency in grain growth microstructures. This is in accord with Patterson’s result¹³ that the highest frequency forms have few or no triangular faces, while those with the most triangular faces are present the least.

The difference between the grain growth and Poisson-Voronoi microstructure can also be observed with respect to λ₂ value in Table 1. The λ₂ values of the most frequent grain topologies in grain growth microstructures are substantially larger than the corresponding ones in Poisson-Voronoi microstructures. This reveals that the availability of the matrix topology description can be used as another tool for distinguishing between fundamental characteristics of different cellular microstructures, besides the reported order of symmetry¹⁰ of grain topology in Weinberg-vector method.

Grain form evolution in grain growth

An important application of the matrix topology description is the highly efficient analysis of the grain topological form evolution during the grain growth process. The fundamental topological events¹³ occurring in three-dimensional grain growth include: Type I – loss of a grain face through disappearance of a neighboring tetrahedron, Type II– grain encounter between grains not formerly touching and Type III – separation of grains sharing a face.

Steele¹⁸ used Schlegel diagrams and the topological events to study the collapsing polycrystal grains, illustrating the possible topological forms of grains by means of downward and horizontal transitions from 8 to 4 faces. Patterson¹³ expands Steele’s original analysis to include other possible grain forms resulting from uphill and horizontal transitions. However, it is difficult to work out all possible grain forms only by hands with the help of Schlegel diagrams and the topological events. That is part of the reasons why the above studies on topological forms are incomplete and terminated at 8-faced grains.

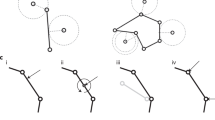
As the grain form evolves based on the topology events, the grain topological matrices will transform at the same time. We can use matrix operation to analyze the possible grain forms in grain growth efficiently. Through the fundamental topological events, a grain topological form would experience 3 possible changes: (1) losing a triangular face, (2) gaining a triangular face and (3) rearrangement of faces¹³. This can be reflected onto grain’s Schlegel diagram (See Fig. 3). Now we give the matrix description of the change (1) losing a triangular face as an example.

Figure 3

Changes of the vertices, edges and faces in Schlegel diagram during grain form evolution.

(a) Losing a triangular face, (b) Gaining a triangular face and (c) Rearrangement of faces. The solid lines and dots denote the edges and vertices after evolution, respectively. The dashed lines and circles denote the original ones.

For convenience, three incidence matrices are constructed depending on the vertices, edges and faces of grain forms. (a) We define the grain topological face-vertex incidence matrix as M^f−v = [m_ij]_n×p, in which m_ij = 1 when the vertex j is in the face i and m_ij = 0 otherwise. (b) We define the grain topological vertex-edge incidence matrix as M^v−e = [μ_ij]_p×q, in which μ_ij = 1 when the vertex i is in the edge j and μ_ij = 0 otherwise. (c) We define the grain topological face-edge incidence matrix as M^f−e = [w_ij]_n×q, in which w_ij = 1 when the edge j is in the face i and w_ij = 0 otherwise. These three incidence matrices have correlations as follows,

The generalized elementary matrices are used in the matrix operation, which include row-deleting matrix (Eⁱ, deleting row i of identity matrix, I) and row-inserting matrix (Uⁱ, inserting a all 0’s row between row (i–1) and row i of I), besides the elementary matrices as row-switching matrix (or permutation matrix, P^i,j), row-multiplication matrix (D^i(c), c≠0) and row-addition matrix (T^{i, j(k)}). It should be noted that c could equal 0 in the generalized matrix D^i(c).

For the change of (1) losing a triangular face, we consider that the mth face of an n-faced grain is a triangular face. Losing this face corresponds to the operation of deleting row m and the three columns with value “1” in M_n^f−e. It is convenient to use the generalized elementary matrices to do matrix operation. That is

where , c₁ < c₂ < c₃. Besides M^f−e,M^f−v and M^v−e can also be obtained by matrix operation. The detailed derivations or explanations of all equations related to the above three topological changes can be seen in the Supplemental Material.

The most realistic means for determining possible grain forms is through the processes causing face-gain or loss in normal grain growth, i.e. encounter, separation and horizontal edge switch transitions within the same face class¹³. We begin with the lone tetrahedron in face class 4 and determine the possible higher forms gradually by uphill and horizontal topology transformations. Firstly, we place a triangular face at any one of the vertices of a grain form in lower face class to get a new grain form in higher face class. Secondly, we do the edge-switch transitions for this form and some other new forms would be created. Thirdly, we do edge-switch transitions again for all forms created in the previous step to find more new forms. The third step was repeated until there are no new forms created. Figure 4 shows the flow chart of the process of the generation of all the possible grain forms. The spectrum of A^f(e) is used to distinguish whether a created form is a new one. Although having the same spectrum is only the necessary condition for two graphs to be isomorphic (i.e., the two forms are the same), it is a practice criterion because there have been found very few examples of non-isomorphic cubic graphs that have the same spectrum¹⁹.

Figure 4

Flow chart of the generation of all the possible grain forms.

This method is able to generate all the possible grain forms, in that any one of f-faced forms can be transformed to all the other forms with f faces by the horizontal edge switch transitions, i.e., rearrangement of faces. The detailed proof is presented in the Supplemental Material and the path of the transition of any two 7-faced grain forms is also included as an example. Figure 5 shows the sketch of the generation of 5- and 6-faced forms from the beginning 4-faced forms.

Figure 5

Sketch of the generation of 5- and 6-faced forms from the beginning 4-faced forms.

The matrix description of grain form evolution in grain growth was implemented by developing a program written in Scilab 5.5.1 (free and open source software for numerical computation, Scilab Enterprises, available from: http://www.scilab.org). Table 2 lists the number of topological forms calculated by this program with a 4 × 3.40 GHz CPU, 16 G RAM computer in an acceptable period of time (e.g., 5 hours for 13-faced grains). For comparison, some similar results are also included. The enumeration of 3-regular simple (3-connected) and band-faced (2-connected but not 3-connected) planar graphs using a Monte Carlo algorithm is done by Keller¹⁵. The number of our calculated grain forms with 3-connected Schlegel diagrams in this work is the same as Keller’s for grains with 13 and fewer faces, but more larger than Keller’s results for grains with 14 faces. Especially, the number of our calculated band-faced planar graphs is larger than Keller’s results for grains with 8 and larger faces. This result indicates that many grain forms are not found by Monte Carlo method of which the reason is still clear. The generated simple graphs by plantri software are a little more than our and Keller’s results for grains with 13 and 14 faces, which is possibly because of the error in judging two same grain forms in different methods and the exact reason still awaits further analysis. The plantri software cannot generate band-faced planar graphs which limits its use in the grain growth studies.

Table 2 Summary of the grain forms generated using our matrix description method, Monte Carlo method¹⁵ and plantri.¹⁵

We plot all the Schlegel diagrams for 8- and 9-faced grains in the Supplementary Material. Figure 6 lists 5 new forms found in this work beyond the known 27 forms for 8-faced grains as reported¹³. They all belong to band-faced topological grain forms and are observed to have characteristic pairs of contiguous three-edged faces. These three-edged face pairs are supposed to be unstable and decompose rapidly¹³ in grain growth process, resulting in relative low frequency of these grain forms in microstructures. It can also be seen that these forms in Fig. 5 have very high symmetry but wide edge distribution of grain faces. This further indicates that high symmetry is possibly a necessary condition for high frequency of occurrence of a certain grain form but not a sufficient condition. Those forms that occur more frequently than others normally have the characteristics of high symmetry plus narrow edge distribution of grain faces, which can be described by the new topology index found in this work-algebraic connectivity.

Figure 6

Five new forms found in this work beyond the known 27 forms for 8-faced grains as reported¹³.

Conclusion

In conclusion, we have introduced an efficient method to completely describe grain topologies. The application of this method to the grain form analysis has shown that the grain growth microstructure favors topological forms with large algebraic connectivity relative to the Poisson-Voronoi microstructure. This suggests that not only highly symmetric topological forms, but also forms with narrow edge distribution of faces are preferred in grain growth microstructure. The algebraic connectivity of grain forms has been proved to be a new convenient differentiator of different multicellular structures. Further, the matrix description of grain topology can serves as a new practical tool to predict the possible grain forms in three-dimensional grain growth efficiently.