Introduction

Percolation (for reviews see Stauffer 19791, Essam 19802) is the random occupation of sites or bonds on lattices or networks, named as site percolation or bond percolation, respectively. Site percolation is more general than bond percolation because every bond model may be reformulated as a site model (on a different graph) and the converse is in general not true3. The appeal of percolation is the occurrence of a critical phenomenon, which has attracted attention for a wide range of applications: liquid flows in porous media4,5, epidemic spread6,7,8, granular and composite materials9,10,11,12, forest fires13,14,15 and fracture patterns and earthquakes in rocks16.

The research originated from homogeneous percolation, i.e., percolation with a single occupation probability. For example, Fisher and Essam (1961) solved homogeneous percolation problems on Bethe lattices17; Sykes and Essam (1964) studied the exact critical occupation probabilities in two dimensions18; Gerald (et al., 2001) derived the value of critical occupation probabilities for a four-dimensional percolation problem on hyper-cubic lattices19.

Building on those results, researchers began to study inhomogeneous percolation20,21,22,23,24,25,26, in which sites (or bonds) may have different occupation probabilities. In 1982, Kesten20 obtained a critical surface of occupation probabilities for inhomogeneous percolation on square lattices. In 2013, Grimmett21 extended the result of inhomogeneous bond percolation to triangular and hexagonal lattices utilizing Russo-Seymour-Welsh (RSW) theory of box-crossings. Recently, Radicchi27 studied percolation on not necessarily infinite graphs and used graph decomposition methods to identify abrupt and continuous changes in percolation.

In the current paper, we focus on inhomogeneous percolation on Bethe lattices. The interest in a good understanding of this inhomogeneous percolation process is twofold. Firstly, Bethe lattices might hold fractal structures, which allow more complex behaviour than square or triangular lattices. The results of this inhomogeneous percolation on Bethe lattices have more extensive applications, e.g., the spreading problem of social networks or infectious diseases (see section III). Secondly, as is well known, most results on percolation are obtained using the heuristic approximation or numerical approaches27,28,29 and it is difficult to get the exact solutions for average cluster sizes and the percolation probability even for homogeneous percolation. In this paper, we investigate inhomogeneous site percolation on Bethe lattices from two occupation probabilities to m occupation probabilities: for the case of two occupation probabilities, we present the explicit formula of the critical occupation probability and the exact solution of average cluster size ; and for the case of m occupation probabilities, because of computational complexity, we formulate and obtain the numerical solutions of average cluster size and percolation probability, which might shed light on deriving the results of inhomogeneous percolation. Besides, we analyse in detail the spread of SARS (an infectious disease) using this inhomogeneous percolation on Bethe lattices with dynamically changing parameters. We present specific control strategies for SARS by comparing the critical infection probabilities, the average numbers of infected individuals for each day, and the probability of the large-scale outbreak of SARS.

Basic theory

In ref. 30 a Bethe lattices is defined to be a tree where each site has Z neighbours, Z is also named coordination number. For the sake of convenience, we denote it as .

On a Bethe lattices, if all sites are occupied randomly with the same probability p, independent of its neighbours, we call the percolation process as homogeneous site percolation and write it as . If the sites of a Bethe lattices are occupied with different probabilities, then the percolation is inhomogeneous. To be concrete, without loss of generality, assume that Z neighbours of each site are occupied randomly with m occupation probabilities , and then, we divide Z neighbours of each site into mdifferent groups (m is the number of types of neighbours according to occupation probabilities), where, of Z neighbours are sites with occupation probability , are sites with occupation probability and are sites with occupation probability. 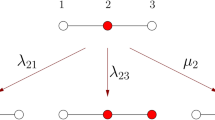The inhomogeneous percolation is indicated with. See Fig. 1 for an illustration of

Figure 1
figure 1

PBL(3; (1, p1), (2, p2)) with 3 sub-generations.

Full size image

In this paper, we first consider inhomogeneous percolation on a Bethe lattices with , that is . Clearly, in this case if or or , inhomogeneous percolation will specialize to homogeneous percolation on BL(Z)30. In a second step, we generalize the results of to the case of .

Critical surface of occupation probability

Occupation probability is the probability with which the sites of a network are occupied. For , assume that a grandparent site is a first type-site on an infinite lattice, then for the parent site, there are sub-branches that begin with the first type-sites and sub-branches beginning with the second type-sites (Fig. 1.). According to the binomial distribution, only branches are accessible on average. On the other hand, if the grandparent site is a second type-site, then for the parent site, there are sub-branches that begin with first type-sites and sub-branches which begin with second type-sites. In this case, on average, only branches are accessible. Recalling that the ratio of these two types of sites is , and according to expectation theory, on average, only

branches are accessible at each step. In order to get an infinite cluster, it is necessary that the quantity (1) is equal or greater than one. Therefore, the critical condition such that an infinite cluster (percolating cluster) first occurs is

from equation (2), we derive the critical surface of occupation probability

this critical surface of is a line with slope in the occupation probabilities set . As an example, see Fig. 2(a) for an illustration of the critical surface of .

Figure 2: Critical surface of occupation probability.
figure 2

(a) Critical surface of occupation probability of . (b) Critical surface of occupation probability of .

Full size image

In a similar way, we can derive the following result.

Theorem 1. The critical surface of is given by

Proof of Theorem 1

For , if the grandparent site is an ith type-site, then for the parent site, there are sub-branches that begin with an ith type-site and nk sub-branches beginning with kth type-sites (Fig. 1). According to the multi-binomial distribution, in this case only branches are accessible on average.

Recalling the occupation probabilities for all types of sites and according to expectation theory, overall, only

branches are accessible on average. In view that is equal to one on the critical surfaces, we have equation (4), the critical surface of .

It is clear that if ; if , where, ; is the percolation probability (existing infinite clusters). The theory generalizes the concept of exact critical value in homogeneous percolation. For consistency, we also indicated the critical surface of by. The critical surface is the subset of the occupation-probability set with all satisfying equation (4). Then, in the supercritical phase, stands for , and there exists almost surely at least one infinite cluster of occupied sites. Contrarily, in the subcritical phase, stands for , and all clusters of occupied sites are almost surely finite. For an illustration, Fig. 3(b) is the critical surface of .

Figure 3: Average cluster size χ(p) of PBL(3; (1, p1), (2, p2)).
figure 3

The left-hand curve is a sketch of the average cluster size and the right-hand curve is a sketch of the mean size of finite clusters of occupied sites when .

Full size image

For an intuitive understanding, take as a reference, and, we have from equation (4) that . In this case is degenerated to a critical point, which is consistent with homogeneous percolation (in the supercritical phase, and in the subcritical phase, .

The critical surface of occupation probabilities consists of those probabilities at which the percolation behaviour of the system changes essentially. We can control the percolation behaviour if we know the critical surface of occupation probabilities.

Average cluster size of occupied sites

The average cluster size of occupied sites is the mean size of the finite (non-percolating) clusters of occupied sites. It is closely related to the critical surface of occupation probabilities. We consider and the relationship between and critical surface.

Theorem 2

Assume that the Bethe lattice is infinite with occupation probabilities such that , then the average cluster size of occupied sites of satisfies

where , .

Proof of Theorem 2. If the Bethe lattice is infinite, all sites are equivalent for evaluating the average cluster size of occupied sites. Let be the average cluster size of the centre sites which are of type i , and be the contribution (to the average cluster size) from a sub-branch which begins with a jth type-site and whose parent site is an ith type-site (Fig. 1). Then

where, the first term is the contribution from the centre site itself, the second term is the contribution from the first type branches, and the third term is the contribution of the second type branches.

According to expectation theory, on average, the average cluster size is

Based on definition of inhomogeneous percolation on a Bethe lattice, the following recurrence relations can be concluded

Solving from equation (9), we have from (7) and (8) that

and

where, and .

For or or , equation (6) reduces to .

The average cluster size (of occupied sites) , which is a function of the occupation probability , can reveal the intensity of percolation. For , increases rapidly with p (Fig. 3), and diverges in a power law of the distance between p and pc, as p approaches pc from below. For , there exist infinite clusters of occupied sites and their number increases as . On the other hand, the numbers of finite clusters (of occupied sites) and their sizes are reducing. Therefore, for , the average sizes of finite clusters decrease with p increasing (Fig. 3).

Similarly, generalizing the result to , we first solve from equation (10), where the have the same meaning as above

Then, substitute the solution of equation (10) into equation (11) to get the values of , here .

According to expectation theory, the average cluster size is

Because the explicit expression of is very complex, we provide only the derivation process.

Percolation probability

In this part, we mainly discuss the percolation probability, i.e., the probability that the origin site belongs to a percolating infinite cluster. Percolation probability is indicated as that can reveal the intensity of percolating, for (Fig. 4).

Figure 4
figure 4

Percolation probability P∞(p) of PBL (3; (1, p1), (2, p2)).

Full size image

For , in order to determine , let denote the probability that an ith type origin site belongs to a percolating infinite cluster, where , .

A site belongs to a percolating infinite cluster, which means, not only the site itself is occupied, but also at least one of the branches (originating from the site) connects to the percolating cluster. Both of these are independent of each other, so, . According to mean theory, it can be concluded that

where, , is the probability that a sub-branch does not connect to the percolating cluster and the sub-branch begins with a jth type-site, whose parent site is an ith type-site. Then, we have

for each equation of (14), the first term is the probability that the root site of a sub-branch is not occupied and the second term is the probability that the root site of the sub-branch is occupied but no child sub-branch connects to the percolating cluster.

If , equation (14) has only the trivial solution , then from (13) we have (Fig. 4). If , there is a nontrivial solution for equation (14) and then equation (13) has a nonzero solution. In this case, it is not easy to get the exact nontrivial solution of equation (14) for it is a set of multivariable high-order equations. By employing fixed-point iteration, we get a numerical solution of equation (14) instead and then obtain the percolation probability from (13). From the numerical solution (Fig. 4), it can be seen that picks up abruptly at pc then increases rapidly with p increasing.

We extend the result to by a similar analysis. In this general case, satisfy meaning the same as above)

Firstly, derive the solution of (15) by fixed-point iteration, and then substitute into (16),

This way, we get , where .

Percolation model of the disease spreading (SARS in Beijing, 2003)

Severe acute respiratory syndrome (SARS) is a viral respiratory illness caused by a corona-virus. In Beijing (China), about 2523 cases have been infected with SARS in 2003. At the beginning of emergence, because of the lack of understanding of SARS and the high mobility of the modern-social activities, SARS spread rapidly. Afterwards, when people found the high infectivity and death rate of SARS, they begun to limit social activity of the public and take strict isolated measure to prevent the spreading of disease then the disease was contained. Is this the proper infection control measure of SARS? Which kind of infectious diseases are suitable for this approach?

In fact, the spreading of SARS is a percolation process. Considering the differences of physical resistibility or intimate contact with the infected individual, we divided people into two groups: the people with higher infection probability (e.g., infants and elderly or healthcare workers), named as susceptible persons; and the people with lower infection probability, named as common persons. Then this disease is modelled as inhomogeneous percolation on Bethe lattices with two occupied probabilities, i.e., . Here, Z is the average contact number of each person, S (of Z) denotes susceptible persons with infection probability p and Z-S (of Z) is common persons with infection probability kp .

The first case of SARS was confirmed on March 5 (in Beijing, 2003) and the government started reporting the cases from April 20. According to case-reporting data from April 20 to June 23 (in Beijing, 2003) (from the government bulletin) and the control activities of government, we find three other critical time points of SARS: May 1 (it is legal holidays from May 1 to May 7), May 14 (people generally panicked over SARS and limited their social activities), and May 30 (new cases of SARS considerably decreased). Correspondingly, the spreading process of SARS was divided into five stages. Then, by random simulation, we found that the spreading of SARS has a fifteen-day time delay. Therefore, we changed the five stages of the spreading process of SARS into: stage 1—from March 20 to May 4, stage 2—from May 5 to May 15, stage 3—from May 16 to May 28, stage 4—from May 29 to June 13, and stage 5—from June 14 to June 23.

In the initial stage, the average contact number of one infected patient was around fifteen , in which two or three person had infected SARS (Gong et al.31), so the infection probability was around . We take according to the percentage of susceptible people in the population and we set by statistical investigation. It is worth noting that the infection probability p is the manifestation of the spreading intensity of the disease, which can only be slightly affected by the protective approach. Therefore, the infection probability was adjusted to 0.1425 in the second stage and third stage, and was adjusted to 0.141 in the fourth stage and fifth stage. The other parameters, i.e., Z and S would change with prevention (isolation of infected patient and restriction of travel) and k remains unchanged in different stages. By statistical investigation, we set Z = 13 and S = 4 in second stage, Z = 12 and S = 3 in third stage, Z = 11 and S = 3 in fourth stage, Z = 8 and S = 2 in fifth stage.

Obviously, the spreading model of SARS (in Beijing) is inhomogeneous percolation on a Bethe lattice with dynamically changing parameters. See Table 1 for the model division and the parameters.

Table 1 The results of inhomogeneous percolation of SARS and some parameters by simulation and statistical analysis.
Full size table

Results of percolation model and control measures

From equation (3), equation (6), and equation (13), we acquire the critical infection probabilities, average number of infected individuals, and the probability of large-scale outbreak for the SARS percolation model in different spreading stages (Table 1).

It can be concluded from Table 1, that, if one is infected with SARS and would live as a normal person, then the disease would infect a massive crowd of healthy people except for and . That warns us, at the initial stage of SARS, humankind should try their best to find SARS patients as early as possible and isolate them from healthy people. Nevertheless, during the incubation period, it is inevitable that some infected persons, who cannot be found and live as the normal person around us that is quite dangerous. At this time, the most effective way is to reduce outdoor activities of public then cut down the average contact number.

For more accurate and meticulous disease-control strategies, we scrutinized the dynamic-dependent relationship between and the average number of infected cases with subtle parameters by a Monte-Carlo simulation. In the initial stage of the SARS process, from March 20 to April 8, according to the above analysis, , and , based on these, the average number of infected cases of each day was simulated. See Fig. 5(a) for an illustration. It is clear that the random variation of the infected number has an incremental trend and that implies that the disease would infect a large amount of persons. Then from April 9 to April 19, during the second stage of SARS, some protective measures were taken with the understanding of the disease, so parameters changed to , and . By simulation, we found that the infected number changes chaotically as in Fig. 5(b). With the time going by, from April 20 to May 4, the severity of the disease gradually being known, more protective measures were taken and parameters reduced further to , and . In this stage, the simulation revealed that the average infected number of each day fluctuates with a trend of decline and it would be zero after a period, which predicates the infectious disease can be controlled without any additional measures (Fig. 5(c)). In fact, by simulating the percolation, we acquire in the initial stage, in the second stage, and in the third stage, i.e., the initial stage is a supercritical phase of the spread of SARS, the second stage is a critical phase, and the third stage is a subcritical phase, which agrees with the simulation. We could conclude that, near the critical point, slightly adjusting of the system parameters would cause a fundamental change of the trend of infectious diseases. Therefore, in order control the large-scale outbreak of the disease, we must try our best to make , even if the infection probability is only a little smaller than the critical infection probability. Actually, if , the probability of a large outbreak of SARS is zero; and if p reaches and crosses , the probability picks up as a power law with exponent one in terms of p-pc, and the disease will outbreak rapidly.

Figure 5
figure 5

The average number of infected individuals versus every day with infection probabilities that are larger, equal, and smaller than critical infection probability.

Full size image

As we know, reducing outdoor activities of the public is a powerful strategy for infectious disease with latent period but it severely obstructs the people’s daily life and social economy. The methods in this paper will supply a quantitative measure for the risk of disease outbreaks and to guide our practice more appropriately.

Predictions

Based on the model of the spreading of SARS, we could supplement the data of cases from March 5 to April 20, during which the recording data was missing. See Fig. 6.

Figure 6
figure 6

Simulation results (a) Cumulative cases of SARS with simulation data and actual data. (b) Daily new cases of simulation and report. (c) The cumulative cases and daily new cases by simulation.

Full size image

Figure 6(a) is the actual cumulative case-reporting data and simulative data. New cases of each day are displayed in Fig. 6(b). We can find that the inhomogeneous percolation is in good fitting with the dynamic process of SARS spreading and time delay is the considerable feature of SARS. The relationship between cumulative confirmed cases and cases out of effective control displays in Fig. 6(c). It can be seen that there will be many persons infected with SARS even if only a few cases of SARS are out of effective control.

Sensitivity analysis

The sensitivity index is the ratio of the change in output to the change in input of parameters or variables32. Taking into account the characteristics of the model, we employ a one factor at a time (OAT) approach, which is more agile and easy to interpret. The popular sensitivity index of OAT approach is , where Y is the output, θ is the input, is the sensitivity index of Y to θ, and is the partial derivative of Y with respect to θ. The quotient is introduced to normalize the index by removing the affects of units33.

First, we get from equation (3), and then derive that:

Where, is the critical infection probability, one of the output of the SARS-percolation model; denote the average contact number of each patient, the number of susceptible persons of Z, the ratio of infection probabilities of susceptible person to common person (see page 12), respectively. They are all input parameters.

Based on the Table 1, the sensitivity indexes of to three input parameters at five critical time points are obtained, which are all negative scalars. These suggest that the decreasing of each input parameters correspond to the increasing of . Among them, the absolute value of is about 0.8, which is maximum, is about 0.5, and is about 0.3. It is clear that has greater sensitivity to Z. See Fig. 7(a) for an illustration.

Figure 7
figure 7

Sensitivity index (a) Sensitivity index of critical infection probability to input parameters-Z, S and k on five critical days of SARS in Beijing (2003) (b) Sensitivity index of the average infected cases by one patient to input variable p (infection probability). (c) Sensitivity index of the probability of SARS large-scale outbreak to input variable p.

Full size image

By a similar analysis with a numerical approach, we obtain and . The sensitivity index is shown in Fig. 7(b). It indicates that is more sensitive near the . Since is the average size of all-finite clusters of infected cases, the exhibits negative value when p is greater than . By a numerical approach, the sensitivity of the probability of large-scalar outbreak of SARS is displayed in Fig. 7(c). has similar characteristics as . They are both more sensitive near the .

Conclusion

In this paper, we present a theoretical framework for inhomogeneous site percolation on Bethe Lattices, and apply it to investigate a diffusion problem of an infectious disease. It is found that the inhomogeneous percolation on Bethe lattices serves as an appropriate model to describe the dynamic spreading behaviour of the infectious disease (SARS). The percolation model of SARS is not only in good agreement with the actual recorded data, but also can be used to predict the future trend of the disease and supply the missing data of the past. Moreover, it can provide quantitative results for government to make more proper disease-control strategies.

Additional Information

How to cite this article: Ren, J. et al. How Inhomogeneous Site Percolation Works on Bethe Lattices: Theory and Application. Sci. Rep. 6, 22420; doi: 10.1038/srep22420 (2016).