Abstract
Evapotranspiration (ET) is the process by which liquid water becomes water vapor and energetically this accounts for much of incoming solar radiation. If this ET did not occur temperatures would be higher, so understanding ET trends is crucial to predict future temperatures. Recent studies have reported prolonged declines in ET in recent decades, although these declines may relate to climate variability. Here, we used a well-validated diagnostic model to estimate daily ET during 1981–2012 and its three components: transpiration from vegetation (Et), direct evaporation from the soil (Es) and vaporization of intercepted rainfall from vegetation (Ei). During this period, ET over land has increased significantly (p < 0.01), caused by increases in Et and Ei, which are partially counteracted by Es decreasing. These contrasting trends are primarily driven by increases in vegetation leaf area index, dominated by greening. The overall increase in Et over land is about twofold of the decrease in Es. These opposing trends are not simulated by most Coupled Model Intercomparison Project phase 5 (CMIP5) models and highlight the importance of realistically representing vegetation changes in earth system models for predicting future changes in the energy and water cycle.
Similar content being viewed by others
Introduction
Terrestrial ET is a key component of the energy and water cycles over global land1. It is the second largest component of the hydrological cycle after precipitation2,3. Variation of terrestrial ET influences precipitation1 and land surface water availability in water bodies, such as lakes and rivers. ET is the second largest component in the surface energy balance after net radiation1. Change in terrestrial ET and its associated latent heat flux, will impact the sensible heat flux by changing land surface temperature, having important implications on regional and global warming4.
Recent studies have focused on ET trends in last several decades and have attributed the ET trends to regional drought1, climate change5, or internal climate variability6. In addition to potential discrepancies in the direction and cause of these changes, the relative contribution of the three main components of ET (i.e., Et, Es and Ei) to these global trends remains unknown. ET components can respond differently to changes in environmental conditions and/or vegetation. For example, while Et is dependent on plant phenology and water-use efficiency, Es is mostly driven by the atmospheric demand for vapour, the availability of water in the soil and the amount of vegetation above the soil and Ei by the occurrence of rainfall and the characteristics of the vegetation stand.
Several studies report the partitioning of global land surface ET, mainly using global land models7 or isotope observations8,9. Although Et is a major component of ET, the global ratio of Et to ET remains uncertain9. More importantly, it is not clear how the ET components contribute to annual trend and variability in ET. To unravel the key mechanisms behind the trends in ET and the contribution of each ET component to these trends over the last three decades, we used the observation-driven Penman-Monteith-Leuning (PML)10,11 model. The PML model has been chosen because of its sound physical basis, simple parameterization and relatively straightforward application10,11,12; furthermore, it can be implemented globally and at high spatial and temporal resolutions, when forced with readily-available gridded meteorological13,14,15 and satellite data16,17.
Results
Model validations
The PML estimated ET and its partitioning are comprehensively assessed from point to global scale, including: (i) catchment precipitation (P) and streamflow (Q) data; (ii) eddy-covariance flux tower data; (iii) satellite-derived soil moisture; (iv) field experiments of ET partitioning; (v) comparing annual Ei/P ratio in homogeneous forests; (vi) evaluation of Es in extreme climates; and (vii) model inter-comparison. This assessment includes five validations, being (i) to (v) and two evaluations, (vi) to (vii); all are outlined below in-turn.
First, over a long-term catchment water balance, ‘observed’ mean annual ET is the difference between the observed catchment mean annual P–Q. The PML estimated ET compares well with long-term water-balance ET observations from 643 largely unregulated large (>2000 km2) catchments across the world (Fig. 1a), with coefficient of determination R2 = 0.87 and Bias = −1.4%. The time-series of aggregated estimated annual ET from the 643 catchments also show good correspondence to the annual P–Q aggregated series (Fig. 1d, R2 = 0.65). This indicates a good performance of the annual ET simulations. In addition, PML-estimated ET trend compares reasonably well to the catchment annual P–Q trend for 46 large unregulated catchments (>10,000 km2) distributed across North America, Europe, South America and Australia (Fig. 1b, R2 = 0.40). It is noted that the catchment annual P–Q trend may have noticeable errors in some catchments due to the influence of catchment storage changes.
Validation of the PML-ET model.
(a) Comparison of the estimated mean annual ET (1981–2012, mm year−1) to catchment ET (P–Q) observations in 643 catchments (red dots in the global map). (b) Comparison of estimated annual ET trend (mm year−2) to catchment annual ET (P–Q) for 46 large catchments (>10, 000 km2) with less than 3-year missing data. (c) Comparison of the estimated ET (mm month−1) to the measured ET at 95 flux sites (red dots in the global map). (d) Annual anomalies of the estimated ET, ET components and catchment observed ET (P–Q), all aggregated from catchments (number of catchments per year provided using grey bars) with annual Q observations. (e) Annual anomalies of the estimated ET, ET components and the observed microwave soil moisture, all aggregated between 40 °N and 40 °S (area covered by the microwave soil moisture data). Error bars for ET and its components are s.d. obtained from the two PML simulations. Error bars for P–Q are s.d. obtained from the two precipitation datasets. R2 in Fig. 1(a–d) is obtained from comparing measured ET and estimated ET. R2 in Fig. 1(e) is obtained from comparing soil moisture and estimated Es. The maps were generated using a commercial software MATLAB.
Second, at monthly scale, the estimated ET is compared to eddy-covariance flux measurements in 95 flux towers widely spread (Fig. 1c), yielding a good agreement indicated by R2 = 0.77 and Bias = −6.0% (Fig. 1c). To test the robustness of the PML model for simulating ET in various climatic conditions, we split the 95 flux towers into two groups: dry and wet. The 16 sites with aridity index (the ratio of potential evapotranspiration to precipitation) more than 1.5 are deemed as ‘dry’; and the 79 sites with aridity index less than 1.5 classified as ‘wet’. Monthly estimated ET corresponds well to the measured in both dry (R2 = 0.77 and Bias = −9.7%) and wet (R2 = 0.77 and Bias = −5.3%) climatic conditions, demonstrating that the PML model performs equally well in both dry and wet conditions.
Third, the ET partitioning into its respective components is also independently evaluated. The annual Es series estimated by the PML model shows good agreement with the TRMM (Tropical Rainfall Measuring Mission) soil moisture estimates (aggregated over 40 °N–40 °S TRMM coverage but excluding grid cells with over tropical forests where soil moisture retrieval is difficult), with R2 = 0.71 (Fig. 1e).
Fourth, the ET partitioning is also checked against 12 field experiments covering various ecosystems for which the Es/ET percentage ratio is obtained (Table 1). The Es/ET percentage ratio estimated by the PML model corresponds well to the results obtained by the field experiments, with R2 = 0.79.
Fifth, the annual Ei/P percentage is also compared to measurements in 11 largely homogeneous inland forest sites (Table 2). Most sites are in humid tropical forests where Ei likely accounts for a significant proportion of ET. Both measurements and estimates show narrow ranges of Ei/P percentage ratios. The measurements show that about 8–14% of annual P is partitioned to Ei for the selected forests, which are similar to the PML estimates that vary from 5% to 11%.
Sixth, the ET partitioning can be qualitatively evaluated in extreme climates, such as deserts in Sahara, central Asia, Arabian Peninsula and central Australia where mean annual potential ET is more than 10 times of mean annual P (Fig. 2a). In these areas, most of precipitation is used for Es, as estimated by the PML model (Figs 2c and 2d).
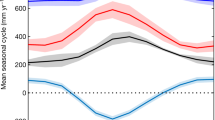
Seventh, the ET estimates from the PML model are also compared to other two diagnostic models (MTE1 and GLEAM6), 9 land surface models1 and 39 Coupled Model Intercomparison Project Phase 5 (CMIP5) climate models18 (Fig. 3). The PML model shows reasonable agreement to the median of the nine land surface models, MTE and GLEAM in the annual global average ET estimates: R2 of 0.69, 0.52 and 0.31, respectively and shows the least agreement to the median of 39 CMIP5 models: R2 of 0.14. All the three diagnostic models show significantly increasing ET trend over 1982–2011, being 0.68, 0.32 and 0.38 mm year−2 for PML (p < 0.01), MTE (p < 0.01) and GLEAM (p < 0.1) models, respectively.
Annual global anomalies (mm year−1) in ET.
Outputs from 39 CMIP5 models span from 1982 to 2005; outputs from 9 land surface models are from 1982 to 2008; outputs from other models (i.e., MTE, GLEAM and PML) are from 1982 to 2011. Dash lines show linear trends for the median of nine land surface models (yellow), MTE (blue), GLEAM (cyan) and PML (black), respectively.
Overall, these seven assessments, including five point to regional validations and two global evaluations, give confidence on the ET components used in our analysis.
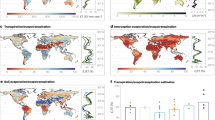
Global and continental summary
The spatial distribution of PML mean annual ET is shown in Fig. 2b. The 1981–2012 mean ET across the global land surface (not considering water bodies and permanent ice surfaces) is 538.1 ± 56.5 mm year−1 (i.e., 63.2 × 103 km3 year−1) (Fig. 4a) or ~67% of mean annual P (805.6 ± 41.7 mm year−1); in good agreement with previous estimates based on similar study periods1,2,3,6. PML Et accounts for ~65% of ET (350.4 ± 54.7 mm year−1), Es for ~25% (133.9 ± 15.0 mm year−1) and Ei for ~10% (53.7 ± 5.5 mm year−1). These estimates fall within the broad range of variability reported by studies based on isotopes8,9 and satellite observations and modelling19,20,21. The relative contribution of the different ET components varies per continent (Fig. 2c,d), reflecting water availability, energy constraints and land cover heterogeneity. Continents containing vast tracts of tropical forests, like South America, evaporate more and the relative contributions from Et and Ei are larger (Fig. 2b,c); whereas in largely arid continents, such as Australia, Es is a substantial contributor (Fig. 2d).
Mean global land surface and continental averages (1981–2012) of various statistics for P, ET, Et, Es and Ei.
(a) Mean annual values (mm year−1). (b) Variance or covariance of annual values (mm2 year−2). (c) Trend (mm year−2). Error bars are s.d. obtained from PML simulations 1 and 2. The symbol ** indicates significance level 1–α = 99% (p < 0.01); the symbol * indicates significance level 1–α = 95% (p < 0.05); the symbol ‘n’ is not significant (p > 0.05). In each figure sub-part for each geographic area the numbers presented are ordered equivalently to the sub-part legend. Note that scaling is applied to the Var (P) on part (b).
Averaged across the global land surface, the inter-annual variance of ET is 1907 ± 147 mm2 year−2, representing only ~6.2% of the P variance (Fig. 4b). The greater than ten-fold difference between P and ET variances is because vegetation and soil serve as ‘storage’ buffers. The Es variance of 967 ± 28 mm2 year−2 is similar to the Et variance globally (958 ± 94 mm2 year−2), despite the Et being more than double Es. This is because some vegetation, especially trees, has access to deep soil water for Et and have developed deep roots in response to P variability22,23. Compared to that, shallow soil water is a more immediate buffer for Es responding directly to the P variability. As a result, global variance in Es is comparable to that in Et, as Es is a larger component of ET in regions with a high inter-annual variability in P, like Australia or South Africa6.
The global multi-decadal trend (1981–2012) in ET is positive (p < 0.01), i.e. in the same direction as previous estimates1,6 (Fig. 3). This is caused by significant positive trends in Et (0.72 ± 0.23 mm year−2) and in Ei (0.14 ± 0.07 mm year−2), which are partly counter-balanced by a significant but smaller negative trend in Es (–0.32 ± 0.07 mm year−2) (Fig. 4c). Strong positive ET trends are observed in northern and eastern Asia, India, eastern North America, Europe, northern Sub-Saharan Africa and northern and eastern Amazonia (Fig. 5a), mainly as a result of increased Et (Fig. 5b). Negative ET trends are observed over parts of subtropical and temperate South America, the Middle East and western United States and are mainly explained by reductions in Es (Fig. 5a,c). Decreases in Es in the Sahel24, Indian Subcontinent and southern China are also accompanied by increases in Et (Fig. 5b,c).
Global maps of trend and correlation (1981–2012).
(a) ET trend (mm year−2). (b) Et trend (mm year−2). (c) Es trend (mm year−2). (d) LAI trend (m2 m−2 year−1). (e) correlation between annual P and annual ET (for land grid cells where p < 0.01, else they are white). (f) P trend (mm year−2). Trends in ET, Et and Es are obtained from the average of the two PML simulations. Trends in LAI are obtained from the AVHRR based LAI product and P trends are averaged from the two P products (i.e., PGF and WFDEI). The maps were generated using MATLAB.
Causality analysis
The contrasting positive trend in Et and negative trend in Es is mostly explained by the increase in leaf area index (LAI) (Fig. 5d). This increasing trend in LAI has been attributed to CO2 fertilization25, global warming26, increased productivity in croplands27, afforestation and forest protection27,28. The increase in LAI also means more shading of the soil surface and less coupling between the atmosphere and the soil surface and these are likely to be the main reasons for the decreasing trend in Es29,30.
The trends in ET and its components due to the observed increase in LAI are further explored as the difference between PML-ET simulations obtained using the observed LAI time series and PML-ET results obtained using detrended LAI time series. The spatial distribution of the trend difference is shown in Fig. 6 and the continental summary of the trend difference is summarised in Table 3. The LAI increase causes noticeable increase in ET (Fig. 6a) in Europe, India, eastern China, eastern and northern Australia, Sahel and eastern Amazon, which is accompanied by an increase in Et (Fig. 6b) and decrease in Es (Fig. 6c). The trend difference in Ei is much smaller compared to that in Et or in Es (Fig. 6d).
Global maps of trend difference.
(a) ET (mm year−2). (b) Et (mm year−2). (c) Es (mm year−2). (d) Ei (mm year−2). Using the PML model, the trend difference is calculated between the average estimates using the observed LAI time series (experiments 1 and 2) minus the average estimates using detrended LAI time series (experiments 3 and 4); details of these experiments are provided in the Methods section. The maps were generated using MATLAB.
The contrasting trends between Es and Et occur mainly in croplands, grasslands, mixed forests and shrublands (see Supplementary Information Figs S1 and S2). Furthermore, the contrasting trends are confirmed when they are stratified using the LAI trend ranging from −0.025 to 0.035 m2 m−2 year−1 (see Supplementary Information Fig. S3).
Globally, the increase in LAI causes an increase in Et and Ei trends by 0.71 and 0.08 mm year−2 and a decrease in Es trend by 0.30 mm year−2 (Table 3). The increase in LAI causes an increase in Et trend for all continents, ranging from 0.57 mm year−2 in Africa to 1.16 mm year−2 in Europe and also causes a slight increase in Ei trend, ranging from 0.04 mm year−2 in Australia to 0.19 mm year−2 in Europe. In contrast, the increase in LAI reduces Es trend for all continents; ranging from −0.18 mm year−2 in North America to −0.56 mm year−2 in South America. These impacts on Et, Es and Ei cause noticeable ET trends increasing in all continents, ranging from 0.30 mm year−2 in North America to 0.84 mm year−2 in Europe.
While the trend in ET is influenced by vegetation change, the ET (and its components) variability is dominated by inter-annual climate variability31. Globally, this is demonstrated by Fig. 7a showing similar variance estimates in annual ET, Et and Es from PML using observed LAI time series and using detrended LAI time series. There is a strong correlation between P and Es (and ET) (Fig. 5e) and the P trend influences Es and ET trends in the southern mid-latitudes, such as the increasing trend in northern Australia and southern Africa and the decreasing trend in southern South America (Fig. 5a,c,f). In these regions, the dynamics of the EI Niño/Southern Oscillation6,32 dominate the multi-decadal P and ET variability. When stratified using the P trend, the ET trend gradually rises with increasing P trend (see Supplementary Information Fig. S4). Furthermore, a decrease in Es trend and Ei trend occurs when the P trend decreases; a strong increase in Ei trend accompanies the strong increase in P trend.
Summary of variance and trend in global ET components and LAI obtained from CMIP5 and PML models for 1981–2005.
(a) variance in ET components (mm year−2). (b) variance in LAI (m4 m−4). (c) trend in ET components (mm year−2). (d) trend in LAI (m2 m−2 year−1). The global variance and trend in the CMIP5 and PML models are obtained using area–weighted average over all land gird cells. All eight CMIP5 models with archived ET, Et and Es outputs are used. Five of the eight models also archived LAI outputs. The model details are summarised in Table S1. Green dots are variance or trend estimated by PML using observed LAI time series (Fig. 7a,c) and are variance and trend in LAI time series (Fig. 7b,d); black dots are variance or trend estimated by PML using detrended LAI time series (Fig. 7a,c) and are variance and trend in detrended LAI time series (Fig. 7b,d). Red crosses are the variance or trend estimated by each CMIP5 model. The bottom, middle and top of each box are the 25th, 50th and 75th percentiles, respectively and the bottom and top whiskers represent the minimum and maximum values.
Discussion
Using the well-validated diagnostic PML model, we estimated that global ET is comprised of 65% Et, 25% Es and 10% Ei. Although Et is larger than Es, their inter-annual variability is similar, because the variability in Et is buffered by vegetation and soil moisture storage. The Es has high inter-annual variability reflecting the high inter-annual variability of P. Regionally, the ET variability is dominated by Et and Ei in densely vegetated and wet regions and by Es in sparsely vegetated and arid regions.
The PML model showed positive trend in ET consistent with and close to, the median (+0.63 mm year−2) of the trends in four other global ET products1,6,33,34. PML and these other four products all show slightly positive ET trends globally of similar magnitude in the last three decades. Over 1981–2012, the PML model estimates positive Et trend of 0.72 mm year−2, which is partially counteracted by a negative Es trend of 0.32 mm year−2. These contrasting trends are primarily driven by the increasing trend in vegetation LAI.
There is a limitation in the PML model in that it does not directly account for the impact of enhanced CO2 concentration on vegetation water use efficiency. To quantify this potential impact, we used the CABLE35 global land surface model which simulates changes in water use efficiency. The experiment was performed using the same forcing data, but with two CO2 concentration forcings: fixed CO2 concentration set at 1981 level and annual CO2 concentration time series from 1981 to 2012. The CABLE simulations show that the change in vegetation water use efficiency due to increasing CO2 concentrations from 1981 to 2012 reduces Et by 0.17 mm year−2 and increases Es by 0.04 mm year−2, hence reducing ET by 0.13 mm year−2. The positive Et trend estimated by the PML model will therefore be smaller (by 20–30%) if the CO2 influence on vegetation water use efficiency is taken into account, but the PML result will still show the strong opposing trends in Et and Es.
We further explore the trends in PML ET components with simulations from the eight CMIP5 models that archive outputs of ET, Et and Es (Fig. 7c) over a common 1981–2005 period. All eight models show positive ET trend, with the PML estimate close to the median of the trend from the eight models. However, the CMIP5 models do not show the contrasting Et and Es trends and generally simulate higher positive trend in Es than in Et. Possible reasons for this may include: (i) a more direct ET response to P in the CMIP5 models thereby implying an insufficient accounting of the vegetation and soil moisture buffering on ET in the CMIP5 models (as seen in the higher variance in ET and its components in the models (Fig. 7a)); and (ii) the limited number of CMIP5 models used here (not all models archive all ET components and there is possible inconsistency in the definition of ET components between models). Also for 1981–2005, we compare observed LAI with simulations from the five CMIP5 models that archived LAI. Results show that the five CMIP5 models overestimate inter-annual LAI variability (Fig. 7b) and do not optimally incorporate LAI to simulate ET components (Fig. 7c) though these five CMIP5 models simulate global LAI greening reasonably (Fig. 7d). Both these findings (i.e., assessing CMIP5 ET and LAI characteristics) suggest the need for better incorporating vegetation dynamics for land-atmospheric interactions in global earth system models to adequately predict future changes in the energy and water fluxes.
Methods
The PML model
At each grid cell, daily ET is the sum of Es, Et and Ei. The PML model estimates Es and Et according to10

where ε = s/γ, in which γ is the psychrometric constant and s = de*/dT is the slope of the curve relating saturation water vapour pressure to temperature;  is the density of air and
is the density of air and  is the specific heat of air at constant pressure;
is the specific heat of air at constant pressure;  is the water vapour pressure deficit of the air (humidity deficit), in which
is the water vapour pressure deficit of the air (humidity deficit), in which  is the saturation water vapour pressure at air temperature and ea is the actual water vapour pressure; Ga is the aerodynamic conductance; Gc is the canopy conductance for transpiration; and f is the fraction of P to equilibrium soil evaporation εAs/(1+ε), estimated from the accumulated precipitation over the previous month11. A, the available energy absorbed by the surface (net absorbed radiation minus soil heat flux), is partitioned using LAI into canopy absorption (Ac) and soil absorption (As). Ei is modelled using an adapted version of the widely adopted Gash rainfall interception model and assumes that the ratio between the wet canopy evaporation rate and the rainfall rate does not vary between storms36. ET estimated at a land grid cell is aggregated from ET estimated from each land cover type within the grid cell.
is the saturation water vapour pressure at air temperature and ea is the actual water vapour pressure; Ga is the aerodynamic conductance; Gc is the canopy conductance for transpiration; and f is the fraction of P to equilibrium soil evaporation εAs/(1+ε), estimated from the accumulated precipitation over the previous month11. A, the available energy absorbed by the surface (net absorbed radiation minus soil heat flux), is partitioned using LAI into canopy absorption (Ac) and soil absorption (As). Ei is modelled using an adapted version of the widely adopted Gash rainfall interception model and assumes that the ratio between the wet canopy evaporation rate and the rainfall rate does not vary between storms36. ET estimated at a land grid cell is aggregated from ET estimated from each land cover type within the grid cell.
There is only one-free parameter, the maximum stomatal conductance ( gsx) to calculate Et in PML. The gsx was estimated for each land cover type using the trial-and-error method by comparing (1) modelled mean annual ET with water balance ET observations (mean annual P minus mean annual Q) and (2) modelled monthly ET with in situ flux tower ET measurements.
At the mean annual scale (1981–2012), the PML model is further constrained by the classic Budyko framework, the Fu hydroclimatic model37 at each grid cell since PML is not constrained by mean annual water balances. The Fu model ensures that mean annual ET is always less than mean annual P for grid cells covered by non-crop vegetation. For cropland, mean annual ET can be larger than mean annual precipitation if irrigation uses groundwater or water transferred from other basins. Therefore, in only those grid cells covered by non-crop vegetation, the three ET components were equally scaled to match the mean annual ET (1981–2012) estimated from the Fu model. There is one parameter  in the Fu model, which was calibrated against catchment ET observations.
in the Fu model, which was calibrated against catchment ET observations.
Data
Meteorological forcings from 1981 to 2012 used to drive the PML model include daily precipitation, air temperature, vapour pressure, shortwave downward radiation, longwave downward radiation and wind speed. The forcings were obtained from two widely used datasets: the Princeton Global Forcing (PGF) data14,15 and the WATCH Forcing Data ERA-Interim (WFDEI) meteorological forcing data13.
Vegetation forcing data were obtained as follows. LAI data from 1981 to 2011 were obtained from Boston University (BU) dataset16. It was derived from the Advanced Very High Resolution Radiometer (AVHRR)-NDVI data. The temporal resolution for the BU dataset is half-monthly and its spatial resolution is 0.0833°. The LAI time series data in 2011 was used for 2012. Emissivity and albedo at 0.05° spatial resolution and 8-day resolution from 1981to 2012 were obtained from the Global Land Surface Satellite (GLASS) dataset38. The GLASS albedo product was produced from both AVHRR (1981–1999) and Moderate Resolution Imaging Spectroradiometer (MODIS) (2000–2012) data. The GLASS longwave emissivity product was generated from both AVHRR visible and near-infrared reflectance from 1981 to 1999 and MODIS seven black-sky albedos ranging from 2000 to 2012. The surface emissivity and mean daily air temperature, was used to estimate daily outgoing longwave radiation, Rlo. Static land cover for 16 land cover types based on the International Geosphere-Biosphere Program (IGBP) Data, generated using 2000–2001 MODIS data, were obtained from the Oak Ridge National Laboratory Distributed Active Archive Center39.
Validation datasets include catchment streamflow, fluxnet eddy covariance ET and over land microwave soil moisture. A total of 643 largely unregulated catchments with a widespread geographic distribution were selected to evaluate model performance at the mean annual scale. To exclude regulated catchments, major dam locations were obtained from three sources: (i) International Commission of Large Dams40; (ii) Meridian World Data (http://www.meridianworlddata.com/) and (iii) National Land and Water Resources Audit of Australia (http://www.nlwra.gov.au/). Daily streamflow data for the selected catchments was obtained from four sources: (i) the Global Runoff Data Centre (located in Germany, http://www.bafg.de/GRDC/EN/Home/homepage_node.html); (ii) the Water Information Research and Development Alliance between CSIRO and Australian Bureau of Meteorology41; (iii) the Model Parameter Estimation Experiment (MOPEX)42 and (iv) the Chinese Academy of Sciences. Each catchment had at least 5 years of observations. Catchment mean annual ET values were estimated as mean annual P minus mean annual runoff (Q), assuming that changes in soil water storage are negligible in the long term43.
A total of 95 fluxnet towers were selected to evaluate model performance at monthly scale. Data for the 93 towers were obtained from the LaThuile FLUXNET dataset. An additional two sites were obtained, one from the OzFlux and another from AmeriFlux. The selected sites span a wide range of climate regimes, covering a total of 11 vegetation types39. These include: grasslands (GRA), evergreen broadleaf forest (EBF), croplands (CRO), mixed forest (MF), evergreen needleleaf forest (ENF), wetlands (WET), open shrublands (OSH), deciduous broadleaf forest (DBF), savannas (SAV), woody savannas (WSA) and closed shrublands (CSH).
Each flux site meets the following criteria: (1) mostly homogeneous land cover at 1 km radius from the flux tower (checked with Google Earth); (2) daily energy balance closure of more than 75%; and (3) more than 2 years of daily data (during days with no precipitation) available. Note here that our evaluation compares the ETPML at 0.50° spatial resolution (i.e., the resolution of the global forcing data) against ETflux representing ET from a radius of tens to hundreds of metres (depending on biophysical, atmospheric and instrumental characteristics).
Annual variation of ET and its components was validated against that of observed soil moisture in sparsely-vegetated regions. The observed soil moisture data were obtained from the radiometer Microwave Instrument on board NASA’s Tropical Rainfall Measuring Mission (TRMM) that started providing passive microwave observations at 10.7 GHz (X-band) and eight higher frequencies including the 37 GHz (Ka) band from December 1997. The observations can be assimilated in a microwave radiation transfer model to infer soil moisture, soil and canopy temperature and vegetation optical depth. We used the top soil moisture retrieved from the Land Parameter Retrieval Model44 based on L- and Ka-band brightness temperatures. The retrieved soil moisture represents the top few centimeters corresponding to 10.7 GHz (X-band). The platform TRMM covers regions between 40 °N and 40 °S. Due to the influence of dense vegetation, reasonable soil moisture retrievals over tropical forests are not available and thus masked out45. The dataset used in this study was resampled to 0.50° spatial resolution and aggregated to monthly average for January 1998 to December 2012.
Modelling experiments
The PML model simulations used two forcing datasets (PGF and WFDEI). Four simulations were run as follows: (1)PML + PGF; (2) PML + WFDEI; (3) PML + PGF (detrended LAI); (4) PML + WFDEM (detrended LAI).
Simulations 1–2 were carried out using observed LAI time series and simulations 3–4 were carried out by repeating the simulations 1–2 but using detrended LAI (i.e. removing the long-term trend, but allowing for sub-annual variation related to seasonal cycles). The difference between simulations 1–2 and simulations 3–4 is used to quantify the impacts of LAI change on trends and variability in ET and its components.
Statistical analysis
Annual variance in ET at each grid cell was partitioned into Et, Es and Ei components and expressed as  . The Mann–Kendall Tau-b non-parametric test including Sen’s slope method46 was used for trend analysis and significance testing.
. The Mann–Kendall Tau-b non-parametric test including Sen’s slope method46 was used for trend analysis and significance testing.
Additional Information
How to cite this article: Zhang, Y. et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 6, 19124; doi: 10.1038/srep19124 (2016).
References
Jung, M. et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 467, 951–954, doi: 10.1038/nature09396 (2010).
Trenberth, K. E., Smith, L., Qian, T. T., Dai, A. & Fasullo, J. Estimates of the global water budget and its annual cycle using observational and model data. Journal of Hydrometeorology 8, 758–769, doi: 10.1175/jhm600.1 (2007).
Oki, T. & Kanae, S. Global hydrological cycles and world water resources. Science 313, 1068–1072, doi: 10.1126/science.1128845 (2006).
Wang, K. & Dickinson, R. E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology and climatic variability. Reviews of Geophysics 50 (2012).
Douville, H., Ribes, A., Decharme, B., Alkama, R. & Sheffield, J. Anthropogenic influence on multidecadal changes in reconstructed global evapotranspiration. Nature Clim. Change 3, 59–62 (2013).
Miralles, D. G. et al. El Niño-La Niña cycle and recent trends in continental evaporation. Nature Climate Change 4, 122–126 (2014).
Lawrence, D. M., Thornton, P. E., Oleson, K. W. & Bonan, G. B. The Partitioning of Evapotranspiration into Transpiration, Soil Evaporation and Canopy Evaporation in a GCM: Impacts on Land–Atmosphere Interaction. Journal of Hydrometeorology 8, 862–880, doi: 10.1175/jhm596.1 (2007).
Jasechko, S. et al. Terrestrial water fluxes dominated by transpiration. Nature 496, 347–351, doi: 10.1038/nature11983 (2013).
Coenders-Gerrits, A. M. J. et al. Uncertainties in transpiration estimates. Nature 506, E1–E2, doi: 10.1038/nature12925 (2014).
Leuning, R., Zhang, Y. Q., Rajaud, A., Cleugh, H. & Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resources Research 44, doi: 10.1029/2007wr006562 (2008).
Zhang, Y. Q. et al. Using long-term water balances to parameterize surface conductances and calculate evaporation at 0.05 degrees spatial resolution. Water Resources Research 46, doi: 10.1029/2009wr008716 (2010).
Morillas, L. et al. Improving evapotranspiration estimates in Mediterranean drylands: The role of soil evaporation. Water Resources Research 49, 6572–6586, doi: 10.1002/wrcr.20468 (2013).
Weedon, G. P. et al. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resources Research 50, 7505–7514, doi: 10.1002/2014wr015638 (2014).
Sheffield, J., Wood, E. F. & Roderick, M. L. Little change in global drought over the past 60 years. Nature 491, 435–438, doi: http://www.nature.com/nature/journal/v491/n7424/abs/nature11575.html#supplementary-information (2012).
Sheffield, J., Goteti, G. & Wood, E. F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. Journal of Climate 19, 3088–3111, doi: 10.1175/jcli3790.1 (2006).
Zhu, Z. C. et al. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sensing 5, 927–948, doi: 10.3390/rs5020927 (2013).
Beck, H. E. et al. Global evaluation of four AVHRR-NDVI data sets: Intercomparison and assessment against Landsat imagery. Remote Sensing of Environment 115, 2547–2563, doi: 10.1016/j.rse.2011.05.012 (2011).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society 93, 485–498, doi: 10.1175/bams-d-11-00094.1 (2012).
Mu, Q., Zhao, M. & Running, S. W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sensing of Environment 115, 1781–1800, doi: 10.1016/j.rse.2011.02.019 (2011).
Schlesinger, W. H. & Jasechko, S. Transpiration in the global water cycle. Agricultural and Forest Meteorology 189–190, 115–117, doi: 10.1016/j.agrformet.2014.01.011 (2014).
Wang-Erlandsson, L., van der Ent, R. J., Gordon, L. J. & Savenije, H. H. G. Contrasting roles of interception and transpiration in the hydrological cycle & ndash; Part 1: Temporal characteristics over land. Earth Syst. Dynam. 5, 441–469, doi: 10.5194/esd-5-441-2014 (2014).
Campos, G. E. P. et al. Ecosystem resilience despite large-scale altered hydroclimatic conditions. Nature 494, 349–352, doi: 10.1038/nature11836 (2013).
Smettem, K. R. J., Waring, R. H., Callow, J. N., Wilson, M. & Mu, Q. Z. Satellite-derived estimates of forest leaf area index in southwest Western Australia are not tightly coupled to interannual variations in rainfall: implications for groundwater decline in a drying climate. Global Change Biology 19, 2401–2412, doi: 10.1111/gcb.12223 (2013).
Dardel, C. et al. Re-greening Sahel: 30 years of remote sensing data and field observations (Mali, Niger). Remote Sensing of Environment 140, 350–364, doi: 10.1016/j.rse.2013.09.011 (2014).
Donohue, R. J., Roderick, M. L., McVicar, T. R. & Farquhar, G. D. Impact of CO2 fertilization on maximum foliage cover across the globe’s warm, arid environments. Geophysical Research Letters 40, 3031–3035, doi: 10.1002/grl.50563 (2013).
Jiang, N., Zhu, W. Q., Zheng, Z. T., Chen, G. S. & Fan, D. Q. A Comparative Analysis between GIMSS NDVIg and NDVI3g for Monitoring Vegetation Activity Change in the Northern Hemisphere during 1982–2008. Remote Sensing 5, 4031–4044, doi: 10.3390/rs5084031 (2013).
Piao, S. L. et al. The carbon balance of terrestrial ecosystems in China. Nature 458, 1009–U1082, doi: 10.1038/nature07944 (2009).
Siry, J. P., Cubbage, F. W. & Ahmed, M. R. Sustainable forest management: global trends and opportunities. Forest Policy and Economics 7, 551–561, doi: 10.1016/j.forpol.2003.09.003 (2005).
Breshears, D. D. The grassland-forest continuum: trends in ecosystem properties for woody plant mosaics? Frontiers in Ecology and the Environment 4, 96–104, doi: 10.1890/1540-9295(2006)004[0096:tgctie]2.0.co;2 (2006).
Adams, H. D. et al. Ecohydrological consequences of drought- and infestation- triggered tree die-off: insights and hypotheses. Ecohydrology 5, 145–159, doi: 10.1002/eco.233 (2012).
Power, S., Delage, F., Chung, C., Kociuba, G. & Keay, K. Robust twenty-first-century projections of El Nino and related precipitation variability. Nature 502, 541–545, doi: 10.1038/nature12580 (2013).
Chiew, F. H. S. & McMahon, T. A. Global ENSO-streamflow teleconnection, streamflow forecasting and interannual variability. Hydrological Sciences Journal-Journal Des Sciences Hydrologiques 47, 505–522, doi: 10.1080/02626660209492950 (2002).
Zhang, K. et al. Vegetation Greening and Climate Change Promote Multidecadal Rises of Global Land Evapotranspiration. Scientific Reports 5, 15956, doi: 10.1038/srep15956 (2015).
Mao, J. et al. Disentangling climatic and anthropogenic controls on global terrestrial evapotranspiration trends. Environmental Research Letters 10, 094008, doi: 10.1088/1748-9326/10/9/094008 (2015).
Wang, Y. P. et al. Diagnosing errors in a land surface model (CABLE) in the time and frequency domains. Journal of Geophysical Research-Biogeosciences 116, doi: 10.1029/2010jg001385 (2011).
van Dijk, A. & Bruijnzeel, L. A. Modelling rainfall interception by vegetation of variable density using an adapted analytical model. Part 1. Model description. J. Hydrol. 247, 230–238, doi: 10.1016/s0022-1694(01)00392-4 (2001).
Fu, B. P. On the calculation of the evaporation from land surface (in Chinese). Sci. Atmos. Sin. 5, 23–31 (1981).
Liang, S. et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. International Journal of Digital Earth 6, 5–33, doi: 10.1080/17538947.2013.805262 (2013).
Friedl, M. A., Strahler, A. H. & Hodges, J. ISLSCP II MODIS (Collection 4) IGBP Land Cover, 2000-2001. In Hall, Forest, G., Collatz, G., Meeson, B., Los, S., Brown de Colstoun, E. & Landis, D. (eds.). ISLSCP Initiative II Collection. Data set. Available on-line [http://daac.ornl.gov/] from Oak Ridge National Laboratory Distributed Active Archive Center, Oak Ridge, Tennessee, USA doi: 10.3334/ORNLDAAC/968 (2010). (Date of access: 22/01/2014)
Vorosmarty, C. J. et al. Anthropogenic sediment retention: major global impact from registered river impoundments. Global and Planetary Change 39, 169–190, doi: 10.1016/s0921-8181(03)00023-7 (2003).
Zhang, Y. Q., Viney, N., Frost, A., Oke, A., Brooks, M., Chen, Y. & Campbell, N. Collation of Australian modeller’s streamflow dataset for 780 unregulated Australian catchments. CSIRO: Water for a Healthy Country National Research Flagship, 117pp (2013).
Duan, Q. et al. Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 320, 3–17, doi: 10.1016/j.jhydrol.2005.07.031 (2006).
Zhang, L., Dawes, W. R. & Walker, G. R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resources Research 37, 701–708 (2001).
Owe, M., de Jeu, R. & Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. Journal of Geophysical Research-Earth Surface 113, doi: 10.1029/2007jf000769 (2008).
Liu, Y. Y. et al. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sensing of Environment 123, 280–297, doi: 10.1016/j.rse.2012.03.014 (2012).
Burn, D. H. & Elnur, M. A. H. Detection of hydrologic trends and variability. J. Hydrol. 255, 107–122 (2002).
Cavanaugh, M. L., Kurc, S. A. & Scott, R. L. Evapotranspiration partitioning in semiarid shrubland ecosystems: a two-site evaluation of soil moisture control on transpiration. Ecohydrology 4, 671–681, doi: 10.1002/eco.157 (2011).
Wilson, K. B., Hanson, P. J., Mulholland, P. J., Baldocchi, D. D. & Wullschleger, S. D. A comparison of methods for determining forest evapotranspiration and its components: sap-flow, soil water budget, eddy covariance and catchment water balance. Agricultural and Forest Meteorology 106, 153–168, doi: 10.1016/s0168-1923(00)00199-4 (2001).
Kostner, B. Evaporation and transpiration from forests in Central Europe relevance of patch-level studies for spatial scaling. Meteorology and Atmospheric Physics 76, 69–82, doi: 10.1007/s007030170040 (2001).
Liu, C. M., Zhang, X. Y. & Zhang, Y. Q. Determination of daily evaporation and evapotranspiration of winter wheat and maize by large-scale weighing lysimeter and micro-lysimeter. Agricultural and Forest Meteorology 111, 109–120, doi: 10.1016/s0168-1923(02)00015-1 (2002).
Kelliher, F. M. et al. Evaporation, xylem sap flow and tree transpiration in a new-zealand broad-leaved forest. Agricultural and Forest Meteorology 62, 53–73, doi: 10.1016/0168-1923(92)90005-o (1992).
Yunusa, I. A. M., Walker, R. R. & Lu, P. Evapotranspiration components from energy balance, sapflow and microlysimetry techniques for an irrigated vineyard in inland Australia. Agricultural and Forest Meteorology 127, 93–107, doi: 10.1016/j.agrformet.2004.07.001 (2004).
Balwinder, S., Eberbach, P. L., Humphreys, E. & Kukal, S. S. The effect of rice straw mulch on evapotranspiration, transpiration and soil evaporation of irrigated wheat in Punjab, India. Agricultural Water Management 98, 1847–1855, doi: 10.1016/j.agwat.2011.07.002 (2011).
Kang, S. Z., Gu, B. J., Du, T. S. & Zhang, J. H. Crop coefficient and ratio of transpiration to evapotranspiration of winter wheat and maize in a semi-humid region. Agricultural Water Management 59, 239–254, doi: 10.1016/s0378-3774(02)00150-6 (2003).
Domec, J.-C. et al. A Comparison of Three Methods to Estimate Evapotranspiration in Two Contrasting Lob lolly Pine Plantations: Age-Related Changes in Water Use and Drought Sensitivity of Evapotranspiration Components. Forest Science 58, 497–512, doi: 10.5849/forsci.11-051 (2012).
Constantin, J., Grelle, A., Ibrom, A. & Morgenstern, K. Flux partitioning between understorey and overstorey in a boreal spruce/pine forest determined by the eddy covariance method. Agricultural and Forest Meteorology 98-9, 629–643, doi: 10.1016/s0168-1923(99)00129-x (1999).
Liu, W., Li, P., Li, H. & Duan, W. Estimation of evaporation rate from soil surface using stable isotopic composition of throughfall and stream water in a tropical seasonal rain forest of Xishuangbanna, Southwest China. Acta Ecologica Sinica 26, 1303–1310, doi: 10.1016/S1872-2032(06)60022-X (2006).
Czikowsky, M. J. & Fitzjarrald, D. R. Detecting rainfall interception in an Amazonian rain forest with eddy flux measurements. J. Hydrol. 377, 92–105, doi: 10.1016/j.jhydrol.2009.08.002 (2009).
Kume, T. et al. Ten-year evapotranspiration estimates in a Bornean tropical rainforest. Agricultural and Forest Meteorology 151, 1183–1192, doi: 10.1016/j.agrformet.2011.04.005 (2011).
Asdak, C., Jarvis, P. G., van Gardingen, P. & Fraser, A. Rainfall interception loss in unlogged and logged forest areas of Central Kalimantan, Indonesia. J. Hydrol. 206, 237–244, doi: 10.1016/s0022-1694(98)00108-5 (1998).
Marin, C. T., Bouten, W. & Sevink, J. Gross rainfall and its partitioning into throughfall, stemflow and evaporation of intercepted water in four forest ecosystems in western Amazonia. J. Hydrol. 237, 40–57, doi: 10.1016/s0022-1694(00)00301-2 (2000).
Lloyd, C. R. & Marques, A. D. Spatial variability of throughfall and stemflow measurements in amazonian rainforest. Agricultural and Forest Meteorology 42, 63–73, doi: 10.1016/0168-1923(88)90067-6 (1988).
Ubarana, V. N. in Amazonian Deforestation and Climate (ed Gash, J. H. C. ) 151–162 (John Wiley, 1996).
Cuartas, L. A. et al. Interception water-partitioning dynamics for a pristine rainforest in Central Amazonia: Marked differences between normal and dry years. Agricultural and Forest Meteorology 145, 69–83, doi: 10.1016/j.agrformet.2007.04.008 (2007).
Shuttleworth, W. J. Evaporation from amazonian rainforest. Proceedings of the Royal Society Series B-Biological Sciences 233, 321–346, doi: 10.1098/rspb.1988.0024 (1988).
Hutjes, R. W. A., Wierda, A. & Veen, A. W. L. Rainfall interception in the tai forest, ivory-coast - application of 2 simulation-models to a humid tropical system. J. Hydrol. 114, 259–275, doi: 10.1016/0022-1694(90)90060-b (1990).
Vernimmen, R. R. E., Bruijnzeel, L. A., Romdoni, A. & Proctor, J. Rainfall interception in three contrasting lowland rain forest types in Central Kalimantan, Indonesia. J. Hydrol. 340, 217–232, doi: 10.1016/j.jhydrol.2007.04.009 (2007).
Valente, F., David, J. S. & Gash, J. H. C. Modelling interception loss for two sparse eucalypt and pine forests in central Portugal using reformulated Rutter and Gash analytical models. J. Hydrol. 190, 141–162, doi: 10.1016/s0022-1694(96)03066-1 (1997).
Acknowledgements
This work was carried out in the Land and Water, CSIRO. We thank Ray Leuning and Michael Roderick for their suggestions on the PML-ET model and thank Martin Jung for his comments and suggestions for validating our results. YYL is the recipient of an Australian Research Council DECRA Fellowship (project number DE140100200). We thank three anonymous reviewers for their constructive comments and suggestions. This work used runoff data collated by the Global Runoff Data Centre, located in Koblenz in Germany. This work also used eddy covariance data acquired by the FLUXNET community and in particular by the following networks: AmeriFlux (U.S. Department of Energy, Biological and Environmental Research, Terrestrial Carbon Program (DE-FG02-04ER63917 and DE-FG02-04ER63911)), AfriFlux, AsiaFlux, CarboAfrica, CarboEuropeIP, CarboItaly, CarboMont, ChinaFlux, Fluxnet-Canada (supported by CFCAS, NSERC, BIOCAP, Environment Canada and NRCan), GreenGrass, KoFlux, LBA, NECC, OzFlux, TCOS-Siberia and USCCC. We acknowledge the financial support to the eddy covariance data harmonization provided by CarboEuropeIP, FAO-GTOS-TCO, iLEAPS, Max Planck Institute for Biogeochemistry, National Science Foundation, University of Tuscia, Université Laval, Environment Canada and US Department of Energy and the database development and technical support from Berkeley Water Center, Lawrence Berkeley National Laboratory, Microsoft Research eScience, Oak Ridge National Laboratory, University of California–Berkeley and the University of Virginia. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP and we thank the climate modelling groups (listed in Table S1 of this paper) for producing and making available their model output and we thank Longhui Li collating CMIP leaf area index dataset. For CMIP the U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.
Author information
Authors and Affiliations
Contributions
Y.Q.Z. designed the study and conducted land surface evapotranspiration modelling and model validation. Y.Q.Z., T.R.M. and F.H.S.C. assessed the importance of vegetation dynamics. Y.Q.Z., J.P.A., H.X.Z., Y.Y.L. and M.P. prepared forcing and validation data. C.L. and Y.P.W. conducted the CABLE modelling. Y.Q.Z., J.P.A., T.R.M., F.H.S.C., J.V., C.M.L., X.J.L., H.X.Z., Y.P.W., Y.Y.L., D.G.M. and M.P. contributed to the text and interpretation.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, Y., Peña-Arancibia, J., McVicar, T. et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci Rep 6, 19124 (2016). https://doi.org/10.1038/srep19124
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep19124
This article is cited by
-
Coupling uncertain patterns of climatic variables in estimating evaporation from open water bodies
Stochastic Environmental Research and Risk Assessment (2024)
-
Notable shifts beyond pre-industrial streamflow and soil moisture conditions transgress the planetary boundary for freshwater change
Nature Water (2024)
-
The maritime continent’s rainforests modulate the local interannual evapotranspiration variability
Communications Earth & Environment (2023)
-
The influence of variations in actual evapotranspiration on drought in China's Southeast River basin
Scientific Reports (2023)
-
Evapotranspiration on a greening Earth
Nature Reviews Earth & Environment (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.