Introduction

A continuous quantum phase transition (henceforth QPT) entails non-analytic behaviour of the ground-state properties of a system at the quantum critical point1,2,3,4. QPT is observed ubiquitously in diverse areas of condensed matter physics and has extensively been studied through last few decades3. Interest in different aspects of it, with many important open issues is nevertheless growing rapidly with time.

One important and long-standing question concerns the existence of the fingerprints of a QPT on higher excited states (i.e., states with finite energy density with respect to the ground state). It is known that QPT has definitive signatures in the ground-state (and low-lying states close to it), as reflected in certain ground-state properties like the derivative of ground-state entanglement (concurrence)5, the ground-state fidelity susceptibility (see, e.g.,6,7,8,9,10,11) or scaling of ground-state entanglement entropy at the critical point(see, e.g.,12,13,14). For a physical (local) Hamiltonian, it is not unexpected for the states moderately close to the ground state (with vanishing energy density) to retain such direct mark of the singularity on them. But as one goes up in energy scale (and hence down in length-scale) the non-universal microscopic details of the system tend to dominate most of the physical properties of the system and the signature of the ground-state singularity gets obscured. This however does not rule out existence of such a signature lying hidden in those excited states in some form.

From the point of view of equilibrium physics, a faint positive indication follows from the existence of the so-called quantum critical region in the finite temperature phase diagram of a quantum system, where the behaviors of the system is strongly affected by the existence of an underlying quantum critical point even at T ≠ 03. Similar indication is obtained from non-equilibrium response mechanism of a system driven at a finite rate across a quantum critical point, largely known as the Kibble-Zurek mechanism15,16, which predicts universal scaling behaviour of defect density with respect to the drive rate. It has been observed that similar to the classical case17,18, the said universality holds even for rapid drives that produces finite density of non-adiabatic excitation also in the quantum case19,20,21,22,23,24.

However, a clear signature of quantum criticality on high-lying states has remained elusive so far. Here we bridge this gap by demonstrating a case where the fingerprints of the QPT on the higher-excited states play an essential role in the occurrence of a non-analyticity in the non-equilibrium response of the system. The signature of the critical point is observed in the energy absorbed by the system from a pulse of large duration. Stronger signature is observed as contribution from higher excited states are incurred by applying pulse of larger amplitude. Though a non-analyticity does not necessarily imply a phase transition (see, e.g.25, where non-analytic behaviour of correlation length is observed at a point with no phase transition), in our case the signature always and exclusively occurs at the critical points.

Results

Consider a quantum many-body Hamiltonian with a set of d independent coupling parameters defining a d-dimensional parameter space, where a position vector represents a set of values for the couplings. We start with the initial state to be the ground-state of with eigenvalue . At t = 0 we apply a pulse of strength r in a given direction by switching the value of from to and again at t = τ, switch it back to (see Fig. 1). The initial energy of the system at t = 0 is the ground-state energy . The final energy of the system (after the pulse is withdrawn) is . The absorbed energy is hence

Figure 1
figure 1

Phase diagram of XY chain in transverse field at T = 0 in the h − γ plane.

The three critical lines (in dashes) are shown - the anisotropy transition in red (along γ = 0, between h = ±1) and the Ising transition lines in blue. Application of an arbitrary pulse in the h − γ plane is illustrated.

Full size image

We show (our main result), that if and only if for a particular value of r (r = rc), corresponds to quantum phase transition point, then the first derivative of Eabs with respect to r is discontinuous at r = rc (a general mathematical argument is given under the heading“General Outline of our Calculation”). Henceforth we drop the arrows and hats when unambiguous. Note that it is actually sufficient to study the final energy of the system instead of Eabs but energy transfer is usually easier to measure than absolute energy.

For the sake of illustration we consider the XY-chain in a transverse field:

where σx,y,z represents the three components of a Pauli spin, γ and h denote the anisotropy and the transverse field respectively (we take ħ = J = 1). The T = 0 phase diagram of the system has three critical lines as shown in (Fig. 1). Pulses of varying height r along a chosen direction in the h-γ plane are applied by changing parameters from to , where , , , δ being the angle between and the positive h-axis (see Fig. 1).

The general expression for Eabs can be obtained as follows. Hamiltonian (2) can be written as direct product of mutually commuting operators , each acting on a separate 2-D Hilbert space spanned by occupation number states and , in the momentum (k)-space (see, e.g.,3,4). Hk has eigenvalues corresponding respectively to eigenvectors and , where . We start at t = 0 with the ground-state of , given by (where super/subscript I and F indicate values corresponding to and respectively. One can express: , where Thus, for 0 < t < τ, the wave function is . Similarly for t > τ, , where (see, e.g.26). The absorbed energy as defined in Eq. (1) is thus in the limit. Now we consider the so called dephasing limit , in which all phases that include τ can be considered rapidly oscillating and are dropped out from the calculation of any physical quantity following Riemann-Lebesgue Lemma (see, e.g.,27). In this limit is hence replaced by . Using this and expressions for ϵk and ϕ (θ), we get

where , and the square root refers to the principal branch. Our quantity of interest is and our main result is that the derivative changes discontinuously as a function of r at r = rc. The analytic expression for the measure of discontinuity (size of the jump in the derivative) is given by

(where the subscripts refer respectively to the values , with η → 0+) which is the quantitative measure of the non-analyticity.

General Outline of our Calculation

The occurrence of the non-analyticity can be qualitatively seen from the general outline of our calculation given in the following. We switch to the complex plane by substituting z = eik in the above expression and convert the integral in Eq. (3) to one over a circular contour with unit radius centering the origin in the z-plane:

where

with

Note that W is analytic within , brings in branch-points into the problem which can be avoided by drawing proper branch-cuts and indenting the contour so that the only singularities enclosed within are the poles, coming from the zeros of z2Q. The non-analytic behaviour of Eabs with respect to r occurs because the pole structure within are different for r > rc and r < rc – poles move in/out of the contour as r is varied across rc. Thus the functional dependence of Eabs on r (which depends on the residues of the poles within ) are in general different on two sides of rc, giving rise to the non-analyticity at (and only at) the critical point. In this context it is interesting to note that no such non-analyticity is observed in Eabs (see Suppl. Mat. ) for a single quench as a function of λF in an XY chain (see e.g.28,29,30). In the following we outline our approach for calculating Δ exactly analytically for pulses in arbitrary directions in the parameter plane.

Crossing the Ising (h = 1) Critical Line

Here we consider pulses from a general initial point (hI, γI) towards a direction δ such that the Ising transition line is crossed (e.g., in Fig. 2c). Evaluating the integral for Eabs (Eq. 4) following the general outline given above (see the Method section for details) we get, for hF = 1, γF ≠ 0,

Figure 2
figure 2

Kink signatures for infinite and finite τ.

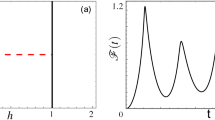
Plot of Eabs for different types of pulses are shown. Clear signatures (kinks) are visible at critical points marked by vertical dotted lines. (a) Eabs vs λF plot for a general type of pulse (λI → λF → λI) starting from hI = 0, γI = 1 in the direction given by tanδ = −0.5. The critical point occurs at λF = 1.118. (b) Eabs vs γF plot for an anisotropic pulse starting from γI = 1.5 with fixed h = 0.2. (c) Eabs vs hF plot for a field-pulse starting from hI = 0.2 with fixed anisotropy, γ = 0.5. (d) Eabs vs hF plot for a transverse Ising model with a transverse field-pulse 0 → hF → 0. For τ = 50, the plots are almost indistinguishable from the infinite τ result, particularly at and around the critical point.

Full size image

where m = tan(δ). Δ = 0 for any other point on the pulse-line that is not a QPT point. This is of course under the assumption that we are considering the nearest point of intersection between the pulse-line and the critical line from the initial point. If the line intersects more than one critical lines, Eabs shows discontinuity (Δ ≠ 0) at each of those (see Fig. 3). A further simplification occurs if we consider the Ising case, i.e., γ = 1, under the h-pulse 0 → hF → 0, where we can calculate the entire analytical expression: for hF ≤ 1 and for hF ≥ 1 (Fig. 2d).

Figure 3
figure 3

(a) Pulse line intersecting two critical lines. This happens for . For this figure, δ = −tan−1 (1.5). (b) Corresponding Eabs vs λF. The present case corresponds to initial point λI = (hI = 0, γI = 1), the pulse direction tanδ = −1.5 and pulse duration τ → ∞. The pulse-line crosses the two critical lines at λF = 0.667 and λF = 1.118 which are the anisotropy critical line and the Ising critical line respectively. The non-analyticity is observed in both the cases.

Full size image

Crossing the Anisotropic (γ = 0) Critical Line

In this case (as in Fig. 2b), when we cross γF = 0 critical line in the region −1 < h < 1, the size of discontinuity is given by

Note that for , the γ = 0 line is not critical since there is no restructuring of the locations of poles (see Methods section).

The Multi-Critical Points (MCP) are characterized by a discontinuity in Δ as a function of δ. Suppose we keep (hI, γI) fixed and vary the pulse direction δ, then Δ(δ) is discontinuous at the values of δ for which the pulse-direction passes through the MCPs at (h = ±1, γ = 0). For example, choosing the initial point to be (hI, γI) = (0, 1), we get the following values of Δ depending on δ within the infinitesimal neighborhood of the MCP.

Crossing More than one critical lines

In some cases, as one increases r , one crosses both the anisotropic critical line and the Ising critical line (Fig. 3a) so that the Eabs − λF curve has two kinks (Fig. 3b) due to (independent) changes in the pole structure twice corresponding to the crossing of two critical points (see Methods Sec. for details).

Signature on the Higher Excited States

Here we show that the non-analyticity in Eabs at λF = λC essentially involves contributions from higher excited states of H(λI) and H(λC). Let and denote the complete set of ortho-normalized eigenstates of H(λI) and H(γF) and . It can be shown that . The overlap vanishes exponentially with N (see, e.g., Ref. 31) and is independent of N Hence the “ground-state-only” contribution vanishes as N → ∞ (note that is nothing but the fidelity between and .) Hence all the terms contributing to Eabs (and hence its non-analyticity) involves higher excited states.

The question that naturally arises is how high can we go up in the energy and still find eigenstates (of the critical Hamiltonian H(λC)) contributing significantly to the signature? One quantitative way of probing this is to monitor the magnitude of the discontinuity Δ as the function of the pulse height r, as one increases it by moving away from the critical point deeper into a phase. An increase in r will result in excitation of higher energy eigenstates of H(λC) and hence more weight of such states in Eabs. Hence, if the signature weakens on the eigenstates of Hc as one goes up in energy, then increase in r is expected to decrease Δ. But here Δ increases monotonically with such increase in r without bound. For example, for crossing the Ising line (Eq. 6), we get and for crossing the anisotropy line (Eq. 7), . This indicates that eigenstates with higher and higher energy (even those with non-vanishing energy density) excited by abitrary increase in r, actually carry the imprint of the critical point, which is filtered out and added up to enhance Δ.

Finally, the state itself, from which we read our signature off, has extensive subsystem entanglement entropy (proportional to the linear dimension of the sub-system)32,33. Our signature is thus visible on a non-equilibrium state not only with extensive energy density, but also with extensive entanglement entropy - a state truly far from the ground state manifold.

Signature in Transverse Spin Polarization

Eabs is not necessarily the only quantity from which the non-analytic signature of QPT can be read off. Here we illustrate this by discussing the special case of 0 → hF → 0 pulse, keeping γ constant. The quantity we concentrate on is the total transverse spin polarization . Though , as τ → ∞ one gets , starting with a ground state of H(h = 0) as the initial state. Thus the non-analytic behaviour of Eabs as a function of hF is directly reflected in the behaviour of limτ → ∞Mz(τ) vs hF.

Discussion

Though the models we have studied are integrable, we conjecture that Eabs will continue to bear similar non-analytic signature of continuous QPT in generic systems, at least when rc is small. The intuition is based on the observation that Δ is a continuous function of (hI, γI) for a given critical point, i.e. if we move our initial point towards the transition point (thereby reduce rc), the value of Δ reduces in a continuous manner. This means, even if our pulse height is small enough so that the ground state of H(λI) is a superposition of only the low-lying eigenstates of H(λc), still the discontinuity will persist. But appearance of non-analyticity at criticality due to excitation of only the low energy manifold of H by small perturbations is expected to be universal. Hence existence of such non-analyticities in the tractable models suggests their existence in more generic systems. However, if indefinitely higher excited states will still continue to bear the signature in those cases is an open question.

The entire picture fits in if we assume that , for a given and pulse direction is the property of the equilibrium “phase”, i.e., it is a smooth function as long as the pulse-line between and lies within a single phase. If it crosses a phase boundary (transition line/point), it in general becomes a different smooth function. Hence Eabs shows a non-analyticity at the boundary as a function of .

The above picture allows us to consider Eabs as a powerful substitute of order parameter for a quantum phase transition, with Δ serving as a sharp locator of the critical point. It is well known that identifying the correct order parameter for complex phases of a condensed matter may often prove to be a hard task. Locating a quantum critical point accurately can also be quite difficult. Our result indicates an alternative non-equilibrium route to the solution of these long-standing problems.

In conclusion, we demonstrate that quantum phase transition (QPT) can be detected from a truly non-equilibrium signature exhibited in the energy absorbed by the concerned system from an externally applied pulse. The non-analyticity essentially involves signature of the QPT on high-lying excited states. This opens up possibilities of devising protocols for detecting and confirming quantum critical points in systems where the location of the critical point and the nature of the phases across it are not precisely known.

Many open issues spring to mind. Do similar signatures exist for QPTs other than continuous ones (e.g., for 1st order) or those without local order parameters, like the topological QPTs? Since the signature involves higher excited states, does it persist at low but finite temperature? Finally, how high in energy can one find eigenstates bearing discernible signatures of the low-lying equilibrium quantum phase transition for a generic quantum critical system with local interactions? Of course, one can design a non-local Hamiltonian, say, by choosing independent orthogonal states as the eigenstates of the Hamiltonian, in which case higher excited states will, by construction, have no information whatsoever regarding the nature of the ground state. Hence the indication we obtain here delves into the deeper issues of correlation between the low-lying and higher eigenstates of a local Hamiltonian. These general open questions are likely to trigger further research in the field.

Methods

Here we lay down the details of evaluating Eabs for different cases of crossing the critical lines. In the general expression Eq. (4) of Eabs, the evaluation of the integration of Eabs involves the investigation of positions of poles and branch points in/outside the contour. There are four branch points: z1,2(hI, γI), and five poles: 0 (of order 2), z1,2(hF, γF), (of order 1). Branch points involving (hI, γI) and poles involving (hF, γF) will be denoted by zI and zF respectively. The positions of the poles change depending on the value of hF and γF. The critical lines hF = ±1 and γF = 0 divide the hF − γF plane into four different regions where the poles residing inside the contour are different (elaborated in Fig. 4).

Figure 4
figure 4

Pole structure in the hF − γF plane.

The poles z = 0, , are inside the contour for and γF > 0 (named Region I); z = 0, , are inside for and γF < 0 (Region II); z = 0, , are inside when hF > 1 for all values of (positive and negative) γF (Region III); z = 0, , are inside when hF < −1 for all values of γF (Region IV).

Full size image

First we consider the case of crossing h = 1 critical line from positive γI (Region I to Region III in Fig. 4). The pole z = 0 are always inside in all cases. Of the other four, is always inside and is always outside the contour. However, the pole is inside the unit circle for hF < 1 and outside for hF > 1. The branch points are inside the circle and the contour should be indented to avoid branch lines (Fig. 5, left contour). Since the integral over the indentations are continuous functions of (hF, γF), the non-analyticity in the behaviour of Eabs arises from the restructuring of poles inside the unit circle and we have

Figure 5
figure 5

Contours with poles and branch-point for integrating Eabs (Eq. 4) under different circumstances: The left contour represents the case of crossing the h = 1 line.

zF corresponds to the arguments hF, γF and zI for hI, γI. The right contour corresponds to the case of crossing the γ = 0. zF corresponds to the arguments hF, γF and zI for hI, γI. In both the figures red dotted lines represent the branch-cuts.

Full size image

where A.P. stands for analytic part and Res. for residue of the integrand of Eabs. We then calculate the difference of slope of two sides of hF = 1 to get Eq. (6).

Next we consider the case of crossing γ = 0 critical line. Here all the poles except z = 0 change their positions when γF = 0 is crossed [see Figs 4 and 5 (right contour)]. Thus we get

This equation leads to the evaluation of the difference of slope before and after crossing γF = 0 as in Eq. (7). As mentioned above, the γ = 0 line is not critical for because the poles , remain inside and , remain outside the unit circle for all values of γF. Hence, there is no restructuring of the location of poles and no non-analyticity of absorbed energy in this case.

For pulses applied along a line that cross two critical lines/points, two independent kinks are observed at the two critical points. For example (Fig. 3b), when λF crosses the γF = 0 line, the pole structure changes from inside to inside (see Fig. 4) and Δ is given by Eq. (7). Similarly when the pluse line crosses the hF = 1 line, the pole goes outside and comes inside and Δ is given by Eq. (6).

Additional Information

How to cite this article: Bhattacharyya, S. et al. Signature of a continuous quantum phase transition in non-equilibrium energy absorption: Footprints of criticality on higher excited states. Sci. Rep. 5, 16490; doi: 10.1038/srep16490 (2015).