Abstract
The drying process of graphene-polymer composites fabricated by solution-processingfor excellent dispersion is time consuming and suffers from a restacking problem.Here, we have developed an innovative method to fabricate polymer compositeswith well dispersed graphene particles in the matrix resin by using solventfree powder mixing and in-situ polymerization of a low viscosity oligomerresin. We also prepared composites filled with up to 20 wt% of grapheneparticles by the solvent free process while maintaining a high degree of dispersion.The electrical conductivity of the composite, one of the most significantproperties affected by the dispersion, was consistent with the theoreticallyobtained effective electrical conductivity based on the mean field micromechanicalanalysis with the Mori-Tanaka model assuming ideal dispersion. It can be confirmedby looking at the statistical results of the filler-to-filler distance obtainedfrom the digital processing of the fracture surface images that the variousoxygenated functional groups of graphene oxide can help improve the dispersionof the filler and that the introduction of large phenyl groups to the graphenebasal plane has a positive effect on the dispersion.
Similar content being viewed by others
Introduction
The extraordinary properties of graphene such as its large surface area,outstanding flexibility and transparency, as well as its excellent mechanical,electrical and thermal properties1,2,3,4,5,6,7 havebeen reported since Geim and co-workers at Manchester University successfullyidentified single-layer graphene in 20048. It was consideredpreviously that the material is thermodynamically unstable and unable to existunder ambient conditions9. Graphene-polymer composites havethe potential to be applied to various products such as components of electronicequipment, energy storage media, organic solar cells, heat-conduction composites,film packaging and biomimetic devices due to the extraordinary properties10,11. However, restacking occurs frequently during mixing withthe polymer matrix due to strong van der Waals forces between the graphenefillers and causes cracks, pores and pin holes in the composite. These defectsdecrease the beneficial properties of the graphene-polymer composites10,11,12,13,14,15. Since solution processing requires a longdrying time during the preparation of graphene-polymer composites and generallyresults in restacking during the drying process, a solvent free process isrequired to induce good dispersion of graphene particles in polymer compositesfor commercial applications.
High quality graphene is typically produced using mechanical peeling, chemicalvapor deposition (CVD) and carbonization from solid sources16,17,18.The original mechanical peeling method from highly oriented pyrolytic graphiteyields a small amount of high quality graphene8. Carbonizationfrom solid sources and CVD methods have been used to synthesize large sizegraphene sheets on silicon wafers19,20,21,22,23. The size,thickness and quality of the graphene produced by CVD growth with nickel andcopper substrates may meet specifications required by industrial applications.However, such production methods are not appropriate for mass production ofgraphene fillers. In this respect, the only possible method of producing graphenefillers for fabrication of polymer composites is the liquid exfoliation andreduction of graphene oxide (GO), which process has previously been used toproduce chemically converted graphene (CCG) in large quantities24,25.
Many studies have focused on the three main methods of manufacturing graphene-polymercomposites: in-situ polymerization, solution compounding and melt blending,as summarized in a review by Sengupta et al10. Additionally,many studies have been carried out on graphene composites based on a rangeof polymers including epoxy, polymethyl methacrylate, polypropylene, polyethylene,polystyrene, polyphenylene sulfide, polyamide, polyaniline, phenylethynyl-terminatedpolyimide and silicone rubber as, reviewed by Kuilla11. Thefindings described by the above references demonstrate that in-situ polymerizationand solution compounding help improve the physical properties of compositesby enhancing the dispersion of fillers; however, melt blending is the mosteconomical technique due to the nonuse of a solvent.
In-situ polymerization methods were proposed recently to prepare polymercomposites by utilizing a polymerizable low viscosity oligomer resin withexcellent dispersion state of fillers26,27,28. Hence, thepotential of a solvent free in-situ polymerization method using the oligomermatrix is immense for commercial production of graphene-polymer composites.The solvent free in-situ polymerization method can be discussed by consideringthe unique two dimensional structure and chemical surface properties of graphene.As shown in Figure 1, we have developed an innovativemethod to fabricate polymer composites with well dispersed graphene fillersusing solvent free powder mixing and in-situ polymerization of a low viscosityoligomer matrix. In order to investigate the dispersion state, we used graphenenanoplatelets (GNP), synthesized GO and GO reduced by phenylhydrazine (CCG-P)as fillers in the polymer composites. We also obtained distributions of filler-to-fillerdistance for individual composites and then calculated the mean and standarddeviation of each distribution to evaluate the filler dispersion quantitatively.
Experimental method
Materials
GNP is a unique nanoparticle consisting of short stacks of graphene sheetswith a platelet shape. Three kinds of grade C GNPs (C300, C500 and C750,XG Science, Lansing, MI, USA) were used and the surface areas of C300, C500,and C750 were 300, 500 and 750 m2/g, respectively. GradeC particles typically consist of aggregates of sub-micron platelets that havea particle diameter of less than 2 μm and a typical particle thicknessof less than a few nanometers, depending on the surface area. CBT resin (CBT160) was supplied in powder form by the Cyclics Corporation (Schenectady,NY, USA). The number of butyl groups in the oligomer mixture varied from 2to 7, which variation resulted in a melting point range of 130 to 150°C.The initially molten oligoesters had a low viscosity of approximately 0.02 Pa·s.A tin-based catalyst was included in the CBT resin and the viscosity of theresin increased rapidly with the entropically driven, ring-opening polymerizationof the cyclic oligoesters at temperatures above 160°C. The fully polymerizedoligoesters were converted into polymerized CBT (pCBT) with a structure similarto that of PBT and a density of 1.3 g/cm3.
Synthesis of GO and CCG-P
GO was synthesized using the modified Hummer's method. Graphite flake(KS 150, TIMICAL GRAPHITE & CARBON, Bodio, Switzerland) was added to aflask containing H2SO4 solution (120 ml) andthen stirred for 1 h. In order to oxidize the graphite, a KMnO4solution was titrated into the mixture and the reaction was maintained for5 h. Deionized (DI) water (150 ml) and H2O2(17 ml) were successively added to the mixture, which was incubatedfor 24 h. The exfoliated GO was neutralized in a dialysis tube afterthe mixture was treated in a centrifuge. The GO was finally dried for 48 husing freeze drying equipment. CCG-P was prepared with a phenyl hydrazinereducing agent (see Figure S1). Phenyl hydrazine (2 ml)was added slowly to the reactor with the GO and DI water and the mixture wasmaintained for 6 h. The mixture was filtrated using a vacuum pump andthe resulting cake was then dried in an oven. Details of the characterizationof the fillers are shown in the Supplementary Information.
Fabrication of composites
The used materials were dried overnight at 110°C to eliminate moisturewhich can interfere with the polymerization of the CBT resin. Since the viscosityof molten CBT is as low as 0.02 Pa·s during the first melting,excellent dispersion of fillers can be derived. To maintain the excellentdispersion of the modified graphene fillers, the composites were preparedusing a powder mixing method as shown in Figure 1. Afterthe CBT powder and fillers were weighed with the target weight fraction, theCBT powder and fillers were mixed using a Thinky mixer (ARE 310, Thinky Corporation,Tokyo, Japan) at 2000 rpm for 3 min in order to obtain a uniformlydispersed powder mixture. After the mixed fine powder with weight of 1.5 gwas used to fill a square mold with dimensions of 2.5 cm × 2.5 cmwith 2 mm thickness, GNP-pCBT, GO-pCBT and CCG-P-pCBT composites werethen prepared using a heating press (Daeheung science Co., Incheon, Korea)at 250°C under a pressure of 20 MPa for 2 min. Details ofthe characterization of the composites are shown in the SupplementaryInformation.
Image processing for quantitative evaluation of dispersion
In order to analyze the scanning electron microscopy (SEM) images accurately,a commercial image processing tool (Image Pro-Plus 6, Media Cybernetics, Inc.,Rockville, MD, USA) was used to remove the fracture texture of the SEM imagesand to analyze the average distance between the incorporated fillers in thecomposites. For accurate processing, a sharpening process was performed 2times to emphasize the modified graphene fillers in the fracture surface ofthe SEM images. The fillers in the filtered images were selected with an aspectratio from 1 to 1,000,000 and a length from 0 to 1,000,000 and then highlightedin red (see Figure S2). Statistical data on the distancebetween the filler particles were computed from the digitally processed fracturesurface images.
Theoretical method
The electrical conductivity of the prepared composite was calculated theoreticallybecause the dispersion state of the fillers in the composite can be inferredby evaluating the difference between the theoretically obtained values andthe experimentally measured results.
Mean field micromechanical estimates of effective electrical conductivity
The Mori-Tanaka model29,30,31,32 has been used to estimatethe effective elastic properties of heterogeneous materials, particularlyfor composites containing small amounts of reinforcing fillers in elasticresins. Such approaches are based upon Eshelby's equivalent inclusionmethod33. These mean field approaches are extended in thisstudy to estimate the effective steady state electrical conductivity of compositescontaining different types of heterogeneities with arbitrary shapes, orientations,and interphases between the resin and the reinforcements.
Modified Mori-Tanaka method
A single ellipsoidal heterogeneity embedded within an infinite homogeneousmatrix domain, subject to a constant far-field electric flux, is consideredwhen the Mori-Tanaka method (MTM)29,30,31,32 is appliedto steady state conduction problems. It is assumed for the MTM that the meanelectric field gradient in the matrix has been disturbed by the presence ofother heterogeneities. The continuum average electric flux vector (J)and the electric field gradient (∇φ) are used to predictthe effective electrical conductivity tensor for the composite. The mathematicalrelationships used to determine the electrical conductivity are similar infunctional form to those used to develop the micromechanics models of thermalconductivity for steady state heat flux34. The electrical flowin a composite may be characterized in terms of the far-field applied electricflux vector (J):

where  is the effective second rank electrical conductivity tensor and ∇φis the electrical field gradient, which can be expressed in terms of the electricalpotential, φ. Like the classical Eshelby solution for linear elasticity,for which the strain field inside each heterogeneity is constant, the resultingelectric field gradient inside each heterogeneity is constant when calculatingeffective electrical conductivities.
is the effective second rank electrical conductivity tensor and ∇φis the electrical field gradient, which can be expressed in terms of the electricalpotential, φ. Like the classical Eshelby solution for linear elasticity,for which the strain field inside each heterogeneity is constant, the resultingelectric field gradient inside each heterogeneity is constant when calculatingeffective electrical conductivities.
The second rank electrical conductivity tensor was obtained in this studyby using the formalism established by Nemat Nasser and Hori29to derive expressions for the fourth rank elastic stiffness tensor for multi-phasedcomposites. For a composite with a matrix phase of (0) and a reinforcementphase of (1), the effective second rank electrical conductivity tensor ( ) can be expressed as below.
) can be expressed as below.

where

A(1)is the second rank electrical field concentration tensor for the heterogeneity. σ(0)and σ(1) are the second rank electrical conductivity tensorsfor the matrix and heterogeneity, c1 is the heterogeneityvolume fraction, S(1) is the second rankEshelby tensor for the heterogeneity and I is the second rankidentity tensor. The Eshelby tensor (S(1))accounts for the influence of the aspect ratio and geometry of the heterogeneityon the local electrical field. Eshelby tensors for specific reinforcementshapes, such as spheres, platelets and fibers, are readily available in theliterature34.
It is assumed that the matrix contains m distinct types of ellipsoidalheterogeneities (p = 1, 2,..., m), each consisting of nplayers (αp = 1, 2,..., np; p= 1, 2,..., m). Each type of heterogeneity has distinct electricalproperties, shapes and orientation distributions. The overall effectivenessof the electrical conductivity tensor,  ,for a composite containing m distinct types of heterogeneities (p= 1, 2,..., m), can be expressed as follows.
,for a composite containing m distinct types of heterogeneities (p= 1, 2,..., m), can be expressed as follows.

where

 is the second rank electrical field concentration tensor for the αpthlayer of the pth heterogeneity (αp= 1, 2,..., np, p = 1, 2,..., m). Further,
is the second rank electrical field concentration tensor for the αpthlayer of the pth heterogeneity (αp= 1, 2,..., np, p = 1, 2,..., m). Further,  is the second rank electrical conductivitytensor for the αpth layer of the pthheterogeneity,
is the second rank electrical conductivitytensor for the αpth layer of the pthheterogeneity,  is the volume fractionof the αpth layer of the pthheterogeneity and S(p) is the second rankEshelby tensor common to the heterogeneity and to all layers of the pthheterogeneity. Once the overall electrical conductivity tensor,
is the volume fractionof the αpth layer of the pthheterogeneity and S(p) is the second rankEshelby tensor common to the heterogeneity and to all layers of the pthheterogeneity. Once the overall electrical conductivity tensor,  , is determined for composites containing aligned heterogeneities,the effective electrical conductivity tensors (
, is determined for composites containing aligned heterogeneities,the effective electrical conductivity tensors ( and
and  ) for composites containing 2D and 3Drandomly oriented heterogeneities can be determined using an orientation averagingscheme as described in the Supplementary Information (see Figure S3).
) for composites containing 2D and 3Drandomly oriented heterogeneities can be determined using an orientation averagingscheme as described in the Supplementary Information (see Figure S3).
Micromechanically predicted electrical conductivities
The MTM was used to predict effective electrical conductivity of the compositecontaining GNP (σ(1) = 2.0 × 106 S/m)in the dielectric CBT matrix (σ(0) = 1.0 × 10−13 S/m).The nanoplatelets had a nominal in-plane dimension: length (L) of 2.0 μmand thicknesses (t) of 4.0 (C300), 2.8 (C500) and 1.9 (C750) nm. Suchplatelets can be approximated by oblate ellipsoids (aspect ratio, L/t ≈500, 715 and 1050).
Results and Discussion
The fracture surfaces of composites filled with GNP, GO and CCG-P wereobserved using an SEM and GNPs were dispersed well in the composites eventhough the filler content increased (see Figure S4). Theincorporated fillers were dispersed well in the composite even at 20 wt%filler content, as can be seen in Figure 2. As expected,the electrical conductivity of the composite was improved with respect tothe increase in the filler loadings, as shown in Figure 3.The electrical percolation threshold of the composites filled with C300 andC500 GNPs was observed to have a filler content of around 5 wt% andthat of the composite incorporated with C750 GNP was observed at about 3 to4 wt%. The electrical conductivity of the composite with high loadingof 20 wt% C300 and C500 GNPs did not improve significantly, whereasthat of the highly loaded composite filled with C750 GNP of 20 wt%was enhanced to 16 S/m. The measured electrical conductivity of theGNP-pCBT composite was consistent with the effective electrical conductivitypredicted by the mean field micromechanical estimates found using the Mori-Tanakamodel under assumed ideal conditions. The dispersion of 20 wt% C750GNP filled composite prepared using the proposed composite preparation wassuperior to that of 20 wt% C750 GNP filled composites fabricated bythe typical melt mixing using a Haake Rheomix internal mixer and the ultrasonicationprocessing as explained in Supplementary Information andshown in Figure S5. From these observations, it can beconcluded that the proposed composite preparation method using simple powdermixing and in-situ polymerization based on solvent free processing can induceexcellent dispersion of fillers in composites.
The degree of filler dispersion in composites with 20 wt% fillercontent was determined quantitatively using digitally processed SEM imagesof the fracture surface, as shown in Figures S2 and 2. Based on the average filler-to-filler distance, calculatedby image processing, distance distribution curves were obtained for individualcomposites and then the mean and standard deviation of each distribution werecalculated. GO and CCG-P composites exhibited dispersion superior to thatof GNP composites. The CCG-P composite showed the most uniform dispersion,as can be seen by the standard deviation indicated in Table1.
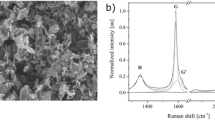
It is well known that the geometry of the fillers is one of the most importantparameters in determining both the dispersion state of fillers and superiorelectrical properties of composites. In particular, thickness and the numberof stacked layers for flake type fillers are influential. Wide angle X-raydiffraction (WAXD) measurement was performed to analyze the number of stackedlayers of the modified graphene fillers and the resulting patterns are shownin Figure 4a. A (0 0 2) diffraction of GO was shownaround a Bragg angle of 11°. The interlayer spacing, calculated from the(0 0 2) diffraction, was 8.08 Å, which is far larger than that of graphite(3.34 Å). The large expansion of the interlayer spacing is ascribedto the insertion of oxygen containing groups and H2O molecules.Because a (0 0 2) diffraction of the GNP appeared at the Bragg angle of 27.5°,the interlayer spacing was 3.34 Å, which indicated the removal of theoxygen containing group and the H2O molecules35.Broader peaks for the (0 0 2) diffraction of the GNP were observed with respectto the increasing surface area of the fillers; this increase in the surfacearea of the fillers was expressed by the number in the grade name, i.e.,the surface area of C300 GNP is 300 m2/g. This impliesthat the surface area of the filler is related to any number of stacked graphiticlayers. In contrast to GO, CCG-P shows two dominant peaks. One peak at 6.7°corresponds to the interlayer spacing of 1.32 nm and this enlargedinterlayer spacing is induced by the phenyl group attached to the graphenelayers. The other broadened peak is centered at 23.5° and correspondsto an interlayer spacing of 3.87 Å, which may be the result of somerestacked graphene layers. Since the spacing is very close to that of pristinegraphite, the functional groups of GO have been efficiently removed36.
Atomic force microscopy (AFM) is usually utilized to investigate the thicknessand number of stacked graphene layers. The thicknesses of C300, C500, C750,GO and CCG-P were 4.0, 2.8, 1.9, 1.0 and 1.0 nm, respectively, withsheet sizes less than 2 μm (see Figure 5).The number of stacked layers of GNP (i.e., C300, C500 and C750) andGO fillers was 12, 8, 6 and 2, respectively, because the interlayer spacingsof GNP and GO were 3.34 Å and 8.08 Å, respectively. It was alsoconfirmed from these results that the number of stacked layers dropped asthe surface area of the GNP fillers increased. Transmission electron microscopy(TEM) is another useful tool for investigating the number of stacked layersin modified graphene fillers. The TEM image results were in good agreementwith the AFM image results and both single and double graphitic layers canbe observed in both CCG-P and GO images (see Figure 5).
The defect levels of the GNPs, GO and CCG-P, which can affect the electricalproperties of graphene composites, were investigated using Raman spectroscopy.As can be seen in Figure 4b, a D band at 1350 cm−1and a G band at 1580 cm−1 were observed in theRaman spectra of GNP. The D-band is a disorder induced feature arising froma double resonance Raman scattering process from non-zero-center phonon modesand is generally attributed to the presence of amorphous or disordered carbons.The G band is caused by in-plane tangential stretching of the carbon carbonbonds in graphene sheets37. The Raman spectrum of GO exhibitedtwo intense peaks at 1328 and 1595 cm−1, whichcorrespond to the D and G bands. The G peak of the CCG-P was red-shifted to1583 cm−1, which shift was similar to that ofGO reduced by hydrazine38. The intensity ratio values of theD band to the G band (ID/IG) were 0.52, 0.43, 0.69, 0.96 and 1.27 for C300,C500, C750, GO and CCG-P, respectively. The ID/IG intensity ratio of CCG-Pincreased to 1.27 (compared with 0.96 for GO), indicating that numerous smallsp2 domains were formed during the reduction reaction39. The GNP filled composite containing relatively thin fillers showedsuperior electrical conductivity because the GNPs had similar defect levelsand also a larger number of fillers allowed electrical percolation to occurat lower filler content level.
The Fourier transform infrared (FT-IR) spectra of GNPs and GO exhibitedrepresentative peaks at 3415, 1730, 1627, 1245 and 1090 cm−1,corresponding to O-H stretch, C = O stretch, aromatic C = C and O-H bending,epoxy C-O stretch and alkoxy C-O stretch, respectively (see Figure4c)40. In the FT-IR spectrum of CCG-P, the C = O andalkoxy C = O peaks increased at the same time as the aromatic C = C peak decreasedgreatly, which meant the introduction of phenyl groups. The surface elementalcompositions of the GNP, GO and CCG-P were analyzed by X-ray photoelectronspectroscopy (XPS). Each peak was fitted to the binding energy of standardcarbon, 284.6 eV. The XPS spectra are shown in Figures6 and S6. The C1s XPS spectrum of GO shows thatthere were three kinds of peaks assigned to oxygen functional groups: hydroxyl,epoxide and carbonyl39. The C1s XPS spectra of the GNP alsoexhibited these peaks but their intensities were much lower than those ofGO, indicating that the oxygen functional groups had been removed. The C1sXPS spectrum of CCG-P revealed that most of the oxygen functional groups wereremoved by reduction with phenyl hydrazine and the C1s spectrum of CCG-P alsoshowed a new peak at 285.8 eV corresponding to C in the C-N bonds ofthe hydrazones41. Therefore, it can be concluded that variousoxygenated functional groups introduced to GO caused the enhanced dispersionof GO in the matrix, with high filler content even though GO based compositesincluded thinner fillers than did GNP based composites and contained a largeramount of fillers at the same content. Furthermore, CCG-P exhibited the highestdegree of dispersion, induced by the introduction of large phenyl groups.
Conclusion
A method of preparing polymer composites using solvent free powder mixingand in-situ polymerization of a low viscosity oligomer resin was applied tofabricate graphene-polymer composites with ultra-high dispersion of fillers.The GNP composites prepared using this method exhibited uniform filler dispersionat a weight fraction of less than 20 wt% and their electrical conductivitywas consistent with the effective electrical conductivity predicted by meanfield micromechanical estimates performed using the Mori-Tanaka model. Inorder to evaluate the filler dispersion quantitatively, the filler-to-fillerdistance was measured for individual composites and then the mean and standarddeviation of the distance were calculated. GO and CCG-P composites exhibiteddispersion superior to that of GNP composites and the CCG-P composite showedthe most uniform dispersion. The GO prepared in this study was thinner thanGNPs and contained hydroxyl, epoxide and carbonyl functional groups attachedto the basal plane. The synthesized CCG-P was the thinnest filler with largephenyl groups. The various oxygenated functional groups of GO caused the enhanceddispersion of GO fillers in the matrix and CCG-P exhibited the highest degreeof dispersion induced by the introduction of large phenyl groups.
References
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Bunch, J. S. et al. Electromechanical resonators from graphene sheets. Science 315, 490–493 (2007).
Wang, S. et al. High mobility, printable and solution-processed graphene electronics. Nano Lett. 10, 92–98 (2010).
Liu, C. et al. Graphene-based supercapacitor with an ultrahigh energy density. Nano Lett. 10, 4863–4868 (2010).
Xia, J. L. et al. Effect of top dielectric medium on gate capacitance of graphene field effect transistors: Implications in mobility measurements and sensor applications. Nano Lett. 10, 5060–5064 (2010).
Mao, Y. et al. High performance graphene oxide based rubber composites. Sci. Rep. 3, 2508/1–7 (2013).
Xu, Y., Li, Z. & Duan, W. Thermal and thermoelectric properties of graphene. Small 10, 2182–2199 (2014).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Mermin, N. D. Crystalline order in two dimensions. Phys. Rev. 176, 250–254 (1968).
Sengupta, R., Bhattacharya, M., Bandyopadhyay, S. & Bhowmick, A. K. A review on the mechanical and electrical properties of graphite and modified graphite reinforced polymer composites. Prog. Polym. Sci. 36, 638–670 (2011).
Kuilla, T. et al. Recent advances in graphene based polymer composites. Prog. Polym. Sci. 35, 1350–1375 (2010).
Naebe, M. et al. Mechanical property and structure of covalent functionalised graphene/epoxy nanocomposites. Sci. Rep. 4, 4375/1–7 (2014).
Li, Y. et al. Highly electrically conductive nanocomposites based on polymer-infused graphene sponges. Sci. Rep. 4, 4652/1–6 (2014).
Yang, Y., Rigdon, W., Huang, X. & Li, X. Enhancing graphene reinforcing potential in composites by hydrogen passivation induced dispersion. Sci. Rep. 3, 2086/1–7 (2013).
David, L. et al. Evaluating the thermal dagame resistance of graphene/carbon nanotube hybrid composite coatings. Sci. Rep. 4, 4311/1–6 (2014).
Huang, X. et al. Graphene-based materials: synthesis, characterization, properties and applications. Small 7, 1876–1902 (2011).
Sun, Z. et al. Growth of graphene from solid carbon sources. Nature 468, 549–552 (2010).
Ruan, G., Sun, Z., Peng, Z. & Tour, J. M. Growth of graphene form food, insects and waste. ACS nano 5, 7601–7607 (2011).
Reina, A. et al. Large area, few-layer graphene films on arbitrary substrates by chemical vapor deposition. Nano Lett. 9, 30–35 (2009).
Li, X. et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009).
Kim, K. S. et al. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 457, 706–710 (2009).
Berger, C. et al. Electronic confinement and coherence in patterned epitaxial graphene. Science 312, 1191–1196 (2006).
Zheng, M. et al. Metal-catalyzed crystallization of amorphous carbon to graphene. Appl. Phys. Lett. 96, 063110/1–3 (2010).
Hernandez, Y. et al. High-yield production of graphene by liquid-phase exfoliation of graphite. Nat. Nanotechnol. 3, 563–568 (2008).
Stankovich, S. et al. Synthesis of graphene-based nanosheets via chemical reduction of exfoliated graphite oxide. Carbon 45, 1558–1565 (2007).
Fabbri, P., Bassoli, E., Bon, S. B. & Valentini, L. Preparation and characterization of poly (butylene terephthalate)/graphene composites by in-situ polymerization of cyclic butylene terephthalate. Polymer 53, 897–902 (2012).
Noh, Y. J. et al. Enhanced dispersion for electrical percolation behavior of multi-walled carbon nanotubes in polymer nanocomposites using simple powder mixing and in-situ polymerization with surface treatment of the fillers. Compos. Sci. Technol. 89, 29–37 (2013).
Kim, S. Y., Noh, Y. J. & Yu, J. Improved thermal conductivity of polymeric composites fabricated by solvent-free processing for the enhanced dispersion of nanofillers and a theoretical approach for composites containing multiple heterogeneities and geometrized nanofillers. Compos. Sci. Technol. 101, 79–85 (2014).
Nemat-Nasser, S. & Hori, M. Micromechanics: Overall Properties of Heterogeneous Materials. North-Holland, Amsterdam, (1993).
Mori, T. & Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metallurgica 21, 571–574 (1973).
Benveniste, Y. A new approach to the application of Mori-Tanaka's theory in composite materials. Mech. Mater. 6, 147–157 (1987).
Mura, T. Micromechanics of defects in solids. M. NijhoffPubl, The Hague (1991).
Eshelby, J. D. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. R. Soc. A 241, 376–396 (1957).
Yu, J., Lacy Jr, T. E., Toghiani, H. & Pittman Jr, C. U. Micromechanically-based effective thermal conductivity estimates for polymer nanocomposites. Compos. Pt. B-Eng. 53, 267–273 (2013).
Rao, C. V., Reddy, A. L. M., Ishikawa, Y. & Ajayan, P. M. Synthesis and electrocatalytic oxygen reduction activity of graphene-supported Pt3Co and Pt3Cr alloy nanoparticles. Carbon 49, 931–936 (2011).
Wang, Y., Shi, Z. & Yin, J. Facile synthesis of soluble graphene via a green reduction of graphene oxide in tea solution and its biocomposites. ACS Appl. Mater. Interfaces 3, 1127–1133 (2011).
Pak, S. Y., Kim, H. M., Kim, S. Y. & Youn, J. R. Synergistic improvement of thermal conductivity of thermoplastic composites with mixed boron nitride and multi-walled carbon nanotube fillers. Carbon 50, 4830–4838 (2012).
Park, S. et al. Colloidal suspensions of highly reduced graphene oxide in a wide variety of organic solvents. Nano Lett. 4, 1593–1597 (2009).
Pham, V. H. et al. One-step synthesis of superior dispersion of chemically converted graphene in organic solvents. Chem. Commun. 46, 4375–4377 (2010).
Pham, V. H. et al. Highly efficient reduction of graphene oxide using ammonia borane. Chem. Commun. 49, 6665–6667 (2013).
Stankovich, S. et al. Stable aqueous dispersions of graphitic nanoplatelets via the reduction of exfoliated graphite oxide in the presence of poly(sodium 4-styrenesulfonate). J. Mater. Chem. 16, 155–158 (2006).
Acknowledgements
This study was supported by the Korea Institute of Science and Technology(KIST) Institutional Program and the Basic Science Research Program throughthe National Research Foundation of Korea (NRF) funded by the Ministry ofEducation, Science and Technology (R11-2005-065). It was also supported bythe Technological innovation R&D program of SMBA [S2177379],the Nano-Convergence Foundation [development and commercialization ofhigh heat dissipative nanocarbon-polymer composites for 25 W/m·K],which is funded by the Ministry of Science, ICT and Future Planning (MSIP,Korea) and the Ministry of Trade, Industry and Energy (MOTIE, Korea) and theWPM (World Premier Materials) Program, Project No. 10037878, UltralightStructural Nano Carbon Composites, funded by the Ministry of Trade, Industryand Energy (MOTIE, Korea).
Author information
Authors and Affiliations
Contributions
Y.J.N. and S.Y.K. conceived the experiments. H.-I.J., S.L. and C.H.L. synthesizedgraphenes. J.Y. performed the calculations. S.H.H. performed the image processing.Y.J.N., S.Y.K. and J.R.Y. wrote the paper. All authors discussed the resultsand commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensedunder a Creative Commons Attribution 4.0 International License. The imagesor other third party material in this article are included in the article'sCreative Commons license, unless indicated otherwise in the credit line; ifthe material is not included under the Creative Commons license, users willneed to obtain permission from the license holder in order to reproduce thematerial. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Noh, Y., Joh, HI., Yu, J. et al. Ultra-high dispersion of graphene in polymer composite via solvent freefabrication and functionalization. Sci Rep 5, 9141 (2015). https://doi.org/10.1038/srep09141
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09141
This article is cited by
-
Modeling of Effective Electrical Conductivity and Percolation Behavior in Conductive-Polymer Nanocomposites Reinforced with Spherical Carbon Black
Applied Composite Materials (2022)
-
Polymer functional group impact on the thermo-mechanical properties of polyacrylic acid, polyacrylic amide- poly (vinyl alcohol) nanocomposites reinforced by graphene oxide nanosheets
Journal of Polymer Research (2022)
-
Comparative investigation on antibacterial studies of Oxalis corniculata and silver nanoparticle stabilized graphene surface
Journal of Materials Science (2022)
-
A comprehensive review on the thermal, electrical, and mechanical properties of graphene-based multi-functional epoxy composites
Advanced Composites and Hybrid Materials (2022)
-
3D Quantitative Light-intensity Dispersion Index of Polymer Nanocomposites Based on Optical Microscopy
Fibers and Polymers (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.