Storage and retrieval of (3 + 1)-dimensional weak-light bullets and vortices in a coherent atomic gas

Abstract

A robust light storage and retrieval (LSR) in high dimensions is highly desirable for light and quantum information processing. However, most schemes on LSR realized up to now encounter problems due to not only dissipation, but also dispersion and diffraction, which make LSR with a very low fidelity. Here we propose a scheme to achieve a robust storage and retrieval of weak nonlinear high-dimensional light pulses in a coherent atomic gas via electromagnetically induced transparency. We show that it is available to produce stable (3 + 1)-dimensional light bullets and vortices, which have very attractive physical property and are suitable to obtain a robust LSR in high dimensions.

Introduction

The investigation of light storage and retrieval (LSR), a key technique for realizing optical quantum memory, has received much attention in recent years^1,2,3. One of important techniques for LSR is electromagnetically induced transparency (EIT)⁴, a quantum interference effect typical occurring in a three-level atomic system interacting with a probe and a control laser fields. The origination of EIT is the existence of dark state, which makes not only the absorption (dissipation) of the probe field largely suppressed but also the LSR possible through an adiabatical manipulation of the control field.

Up to now, nearly all studies on LSR have been carried out in various schemes working in linear regime^5,6. Such schemes are simple but encounter the inevitable problem of pulse spreading due to the existence of dispersion, which may result in a serious distortion for retrieved pulse. Recently, the EIT-based LSR has been generalized to weak nonlinear regime, where the storage and retrieval of a (1 + 1)-dimensional [(1 + 1)D] (i.e., the first ‘1’ refers to one spatial dimension and the second ‘1’ refers to time) soliton pulse is suggested^7,8. However, because the (1 + 1)D soliton pulse is unstable in high dimensions due to the existence of diffraction, such scheme is still not realistic or quite limited. For practical applications of optical quantum memory, a challenged problem is to obtain a light pulse that is robust (i.e., with a high fidelity) during storage and retrieval in (3 + 1)D.

Before proceeding, we note that in recent years there is much effort focused on high-dimensional optical solitons due to their rich nonlinear physics and important applications^9,10. Although in recent works^11,12,13 (3 + 1)D light bullets and vortices in coherent atomic systems have been studied, the possibility of their storage and retrieval is not explored yet to the best of our knowledge.

Here we propose an EIT-based new scheme to realize a robust LSR for (3 + 1)D light pulses in a coherent atomic ensemble working in a free space. Based on Maxwell-Bloch equations governing the evolution of atoms and light field we derive a nonlinear equation controlling the motion of the envelope of a probe field. We show the possibility for obtaining (3 + 1)D light bullets (or called (3 + 1)D spatiotemporal optical solitons^9,10) and vortices, which have ultraslow propagating velocity and extremely low generation power. We further show that these high-dimensional light pulses can be stabilized by using the balance between dispersion, diffraction, nonlinearity and by a far-detuned laser field. We demonstrate that these high-dimensional light pulses can be stored and retrieved very stably by switching off and on a control field.

Results

Model

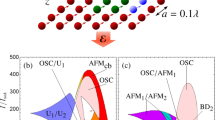
We consider a cold, lifetime-broadened Λ-type three-level atomic gas interacting with a probe field (with pulse length τ₀, center angular frequency ω_p and half Rabi frequency Ω_p) that drives the |1〉 ↔ |3〉 transition and a continuous-wave control field (with the center angular frequency ω_c and half Rabi frequency Ω_c) that drives |2〉 ↔ |3〉 transition; see the inset of Fig. 1(a).

Figure 1

Model and linear dispersion relation.

(a) Possible experimental arrangement of beam geometry. The probe (with angular frequency ω_p and half Rabi frequency Ω_p) and continuous-wave control (with angular frequency ω_c and half Rabi frequency Ω_c) fields propagate nearly along z direction. The (orange) thick arrow denotes the Stark field (with angular frequency ω_s) used to stabilize (3 + 1)D light bullets and vortices. Cold atomic gas are represented by yellow dots. The inset shows the energy-level diagram and excitation scheme of the Λ-type three-level atoms. Δ₂ and Δ₃ are detunings, Γ₁₃ (Γ₂₃) is the decay rate from |3〉 to |1〉 (|3〉 to |2〉). The atoms are initially populated on the ground state |1〉. (b) The linear dispersion relation K(ω) of the probe field as a function of ω.

For simplicity, we assume the electric field propagates along z direction with the form , where is the unit polarization vector (envelope). A fardetuned laser field (Stark field) used to stabilize (3 + 1)D light bullets and vortices (see below) is applied to the system [see Fig. 1(a)] with the form , where e_s, E_s and ω_s are the unit polarization vector, field amplitude and angular frequency, respectively. Due to the existence of the Stark field, an energy shift for the level |j〉 occurs, i.e., . Here α_j is the scalar polarizability of the level |j〉 and denotes the time average in one oscillating cycle.

Under electric-dipole and rotating-wave approximations, the Hamiltonian of the system in the interaction picture reads , with , and . Here Δ₂ = ω_p − ω_c − ω₂₁ and Δ₃ = ω_p − ω₃₁ are respectively the two- and one-photon detunings, p_jl is the electric-dipole matrix element related to the levels |j〉 and |l〉, = E_j − E_l is the energy difference between the level |j〉 and the level |l〉 with E_j the eigenenergy of the level |j〉.

The equation of motion for density matrix σ in the interaction picture reads

where σ is a 3 × 3 density matrix, Γ is a 3 × 3 relaxation matrix denoting the spontaneous emission and dephasing. The explicit expressions of Eq. (1) are presented in Methods.

The equation of motion for Ω_p can be obtained by the Maxwell equation , where with the atomic concentration. Under slowly varying envelope approximation, the Maxwell equation is reduced to ref. 14

where , with c the light speed in vacuum.

Our model can be realized by selecting realistic physical systems. One of them is the ultracold ⁸⁷Rb atomic gas with the energy levels selected as |1〉 = |5²S_1/2, F = 1〉, |2〉 = |5²S_1/2, F = 2〉 and |3〉 = |5²P_1/2, F = 2〉, respectively. The decay rates are given by and and ¹⁵. If atomic density , κ₁₃ takes the value of 3.0 × 10⁹ cm⁻¹ s⁻¹.

Nonlinear envelope equation

We use the standard method of multiple scales developed for EIT system¹⁴ to derive the nonlinear envelope equation for the probe field based on the asymptotic expansion of the Maxwell-Bloch (MB) Eqs. (1) and (2)(see Methods).

The first-order solution of the asymptotic expansion reads , . Here D = |Ω_c|² − (ω + Δ₂ + iγ₂₁)(ω + Δ₃ + iγ₃₁) and θ = K(ω)z₀ − ωt₀, with K(ω) = ω/c + κ₁₃(ω + Δ₂ + iγ₂₁)/D (linear dispersion relation). Note that the frequency and wave number of the probe field are respectively given by ω_p + ω and k_p + K(ω), so ω = 0 corresponds to the center frequency of probe field.

Fig. 1(b) shows the imaginary and real parts of K(ω), i.e., Im(K) and Re(K). The dashed and solid lines are for Ω_c = 0 and for Ω_c = 1.0 × 10⁷ s⁻¹, respectively. From the upper panel we see that for Ω_c = 0 (with no EIT) the probe pulse suffers a large absorption (the dashed line), whereas for Ω_c = 1.0 × 10⁷ s⁻¹ (with EIT) a transparency window opens and hence the probe pulse is nearly free of absorption (the solid line). The lower panel of Fig. 1(b) shows the drastic change of dispersion due to EIT, which results in a significant reduction of the group velocity of the probe pulse.

The solvability condition at the second order of the asymptotic expansion is i[ ∂F/∂z₁ + (∂K/∂ω)∂F/∂t₁] = 0, which means that the probe-pulse envelope F travels with the group velocity V_g = (∂K/∂ω)⁻¹. The nonlinear envelope equation for F is obtained from the solvability condition at the third order, i.e.,

where W₁₁ is the self-phase modulation coefficient of the probe field and W₁₂ is the cross-phase modulation coefficient contributed by the Stark field. The explicit expressions of W₁₁ and W₁₂ are given in Methods.

Combining the solvability conditions (i.e., the equations for F) at the all orders, we obtain the unified equation for F, which can be written into the dimensionless form

with , s = z/L_Diff, τ = [t − z/Re(V_g)]/τ₀, (ξ, η) = (x, y)/R, g₁ = L_Diff/L_Disp, g₂ = L_Diff/L_Nonl, and V(ξ, η) = [E_s(ξ, η)/E₀]². Here U₀, R and E₀ are respectively the typical Rabi frequency, beam radius and field amplitude; L_Diff = ω_pR²/c, and are respectively typical diffraction length, dispersion length and nonlinear length.

Note that the envelope equation (4) includes dispersion, diffraction, nonlinearity and “external” potential. When obtaining Eq. (4) we have neglected the imaginary parts of ∂^jK/∂ω^j (j = 1, 2), W₁₁ and W₁₂. This is reasonable because the system works under the EIT condition so that their imaginary parts are much smaller than their real parts. In addition, the diffraction, dispersion and nonlinearity are assumed to be balanced, i.e., L_Diff = L_Disp = L_Nonl, which can be achieved by taking and and hence we have g₁ = g₂ = 1 in Eq. (4). By taking we also have g₃ = 1. The “external” potential V(ξ, η) in Eq. (4) comes from the Stark field, which can be adjusted and hence useful to control the stability of the light bullets and vortices.

By choosing the realistic system parameters Ω_c = 9.0 × 10⁷ Hz, Δ₂ = −6.0 × 10⁶ Hz, Δ₃ = −2.0 × 10⁸ Hz, R = 40 μm, τ₀ = 2.0 × 10⁻⁷ s, U₀ = 2.87 × 10⁷ Hz and E₀ = 3.04 × 10⁴ V/cm, we have L_Diff ≈ L_Disp ≈ L_Nonl = 1.26 cm and

We see that the probe pulse propagates with an ultraslow group velocity.

Solutions of (3 + 1)D weak-light bullets and vortices

In order to obtain high-dimensional nonlinear localized solutions of the system, we assume the Stark field has the form of Bessel function, i.e., (E_s0 and b are real constants; l is an integer; ). Then Eq. (4) becomes

with v₀ = E_s0/E₀. Note that Eq. (6) is similar to that obtained in Ref. 16. However, the physics here is different from that in Ref. 16 because Eq. (6) describes the nonlinear evolution of the probe-field envelope in the EIT system whereas the equation in Ref. 16 governs the dynamics of a Bose-Einstein condensate. Using the transformation u = ψ exp(iμs), Eq. (6) is reduced into , where μ is a propagation constant.

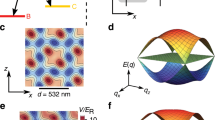
Fig. 2 shows the power of the probe pulse defined by , which is a function of the propagation constant μ and the potential strength constant v₀. Based on the modified squared-operator method¹⁷, (3 + 1)D light bullet solutions are found numerically. Presented in Fig. 2(a) is the result of several light bullet solutions for the potential parameters l = 0 (i.e., the zeroth-order Bessel function) and b = 1. We see that for different values of v₀ (v₀ = 1.3, 2.0, 2.7), P always increases to a maximum firstly and then decreases. The stability domain of the light bullet solutions is the one with dP/dμ > 0 according to Vakhitov-Kolokolov (VK) criterion (see ref. 17), which has been confirmed numerically by using a propagation method. The isosurfaces (|ψ| = 0.05) of stable light bullet solutions for (v₀ = 1.3, μ = 0.5) (the red one), (v₀ = 2.0, μ = 1.9) (the blue one) and (v₀ = 2.7, μ = 4.0) (the green one) have been plotted in the figure.

Figure 2

Solutions of (3 + 1)D light bullets and vortices.

(a) Probe-field power P of several light bullet solutions as functions of μ and v₀, with the Stark field chosen as the zero-order Bessel function (i.e., l = 0). The solid, dashed and dotted-dashed lines are for v₀ = 1.3, 2.0 and 2.7, respectively. Insets give isosurface (|ψ| = 0.05) plots of light bullets for (v₀ = 1.3, μ = 0.5; the red one), (v₀ = 2.0, μ = 1.9; the blue one) and (v₀ = 2.7, μ = 4.0; the green one), respectively. (b) Probe-field power P of the light vortex solution as a function of μ and v₀, with the Stark field chosen as the first-order Bessel function (i.e., l = 1). The green solid line is for v₀ = 2.7. Insets display respectively plots of the isosurface (|ψ| = 0.05) for (v₀ = 2.7, μ = 1.5) of the light vortex and its phase distribution in x-y plane.

Fig. 2(b) shows the result of a light vortex solution for the potential parameters l = 1 (i.e., the first-order Bessel function) and b = 1. The light vortex solution with quantum number of orbital angular momentum m = 1 is found. Because the stability domain of the vortex solution cannot be obtained by the VK criterion, a propagation method is used to study its stability. The isosurface (|ψ| = 0.05) and phase distribution of the vortex solution for (v₀ = 2.7, μ = 1.5) are plotted in the figure. We found that the vortex solution is fairly stable during propagation in the region where dP/dμ > 0.

The threshold of the optical power density for producing the (3 + 1)D light bullets and vortices given above can be estimated by using Poynting's vector¹⁴. For light bullets we obtain

A similar conclusion is also obtained for light vortices. Consequently, to produce (3 + 1)D light bullets and vortices in the present system very low generation power is needed. This is drastically contrast to conventional optical media, such as glass-based optical fibers, where generation power at order of kilowatts or even larger is usually needed to produce light bullets and vortices¹⁸.

Storage and retrieval of (3 + 1)D light solitons and vortices

The principle of EIT-based LSR is well known¹⁹. When switching on the control field, probe pulse propagates in the atomic medium with nearly vanishing absorption; by slowly switching off the control field the probe pulse disappears and gets stored in the form of atomic coherence; when the control field is switched on again the probe pulse reappears. However, this principle is usually applied for linear optical pulses, which may suffer serious distortion due to the dispersion and/or diffraction. In the following we show that it is available to realize the LSR of the (3 + 1)D light bullets and vortices in our present system.

To this end, we consider the solution of the MB Eqs. (1) and (2) by using a control field that is adiabatically changed with time t to realize the function of its turning on and off. The switching-on and switching-off of the control field is modeled by the following function

where T_off and T_on are respectively the times of switching-off and the switching-on of the control field with a switching time T_s. The storage time of the light bullets and vortices is approximately given by T_on − T_off.

We first consider the LSR of the (1 + 1)D soliton pulse, corresponding the case ∂²/∂ξ² = ∂²/∂η² = 0 and g₃ = 0 in Eq. (4). The result of numerical simulation on the time evolution of |Ω_pτ₀| and atomic coherence σ₂₁ as functions of z and t is presented in Fig. 3. The red solid line shown in the upper part of each panel represents the control field |Ω_cτ₀|. Here we choose T_s/τ₀ = 0.2, T_off/τ₀ = 5.0, T_on/τ₀ = 15.0 and the other system parameters are mentioned above. The wave shape of the input probe pulse is taken as a hyperbolic secant one, i.e., Ω_p(0, t) = 7.0 sech(t/τ₀). Lines 1 to 4 are for propagation distance z = 0, 1.5, 3.0 and 4.5 cm, respectively.

Figure 3

Storage and retrieval of (1 + 1)D soliton pulse.

(a) Evolution of |Ω_pτ₀| and (b) atomic coherence σ₂₁ as functions of z and t. For a better visualization, σ₂₁ has been amplified 20 times. Lines 1 to 4 are for z = 0, 1.5, 3.0 and 4.5 cm, respectively. The control field |Ω_cτ₀| is shown in the upper part of each panel.

Shown in Fig. 3(a) is the result of |Ω_pτ₀|. We see that the retrieved pulse has nearly the same shape with the one before the storage. The physical reason of the shape-preservation of the probe pulse before and after the storage is due to a balance between dispersion and nonlinearity, i.e., the pulse is indeed a soliton that is rather stable during the storage and retrieval. Fig. 3(b) shows the atomic coherence σ₂₁, which has been amplified by 20 times for a better visualization. We see that σ₂₁ is nonzero during the switch-off of the control field, which is a manifestation of the information transfer (i.e., storage) from the light field to the atomic ensemble.

We now turn to investigate the LSR of the (3 + 1)D light pulses. Fig. 4 shows the storage and retrieval of the light pulses with the Stark field taken to be the zero-order Bessel function (the left side of each column) and the light pulses with the Stark field taken to be the first-order Bessel function (the right side of each column) for different probe-field intensities, with the other parameters are the same as used above. Isosurfaces (|Ω_pτ₀| = 0.5) for Ω_p0τ₀ = 2.0, 7.0, 10.0 at z = 0 (before the storage), 2.25 cm (during the storage) and 4.5 cm (after the storage) are illustrated, respectively. The results are the following: (i) For the case of weak probe-field intensity (the first line in the figure), the probe pulse broadens before and after the storage; (ii) For the case of moderate probe-field intensity (the second line in the figure), the retrieved probe pulse has nearly the same shape with the one before the storage; (iii) For the case of strong probe-field intensity (the third line in the figure), the retrieved probe pulse displays a serious distortion after the storage. From these results, we conclude that in the regime of the moderate probe-field intensity the storage and retrieval of (3 + 1)D light pulses are robust, which is desirable for light and quantum information processing in high dimensions. This regime is just the one where stable light bullets and vortices can form.

Figure 4

Storage and retrieval of (3 + 1)D light pulses with different probe-field intensities.

Storage and retrieval of (3 + 1)D light pulses with the Stark field taken to be the zero-order Bessel function (the left side of each column) and the (3 + 1)D light pulses with the Stark field taken to be the first-order Bessel function (the right side of each column) for different probe-field intensities (i.e., Ω_p0τ₀ = 2.0, 7.0, 10.0) at z = 0 (before the storage), z = 2.25 cm (during the storage) and z = 4.5 cm (after the storage), respectively. The second line corresponds to the storage and retrieval of stable light bullets and vortices. All figures are isosurface plots with |Ω_pτ₀| = 0.5.

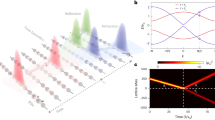
In order to illustrate more clearly the evolution process of the storage and retrieval of the stable (3 + 1)D light bullet and vortex (i.e., the case (ii) described above), in Fig. 5(a), Fig. 5(b) and Fig. 5(c) we show the numerical result of the evolution of the probe field (|Ω_pτ₀|) and the control field (|Ω_cτ₀|) as functions of time at z = 0, 2.25 cm and 4.5 cm, respectively. We see that the light bullet and vortex undergo steps of appearance, disappearance and reappearance. Presented in the first (second) column of Fig. 5(d) is the light-intensity distribution in x-y plane of the bullet (vortex) for t/τ₀ = 5.0, 10.0 and 15.0, respectively. The third column is the phase distribution of the light vortex. The result shows that the light bullet and vortex can be stored around t/τ₀ = 5.0 when the control field is switched off and be retrieved around t/τ₀ = 15.0 when the control field is switched on again. Interestingly, the phase distribution of the vortex can also be stored and retrieved, which means that the memory of the light vortex can bring more information than that of the light bullet.

Figure 5

Robust storage and retrieval of (3 + 1)D light bullet and vortex.

(a), (b), (c) Evolutions of |Ω_pτ₀| as function of t at the position z = 0, z = 2.25 cm and z = 4.5 cm, respectively. Insets are isosurface plots (|Ω_pτ₀| = 0.5) of the light bullet and vortex. (d) Light-intensity distribution of the light bullet (the first column) and the vortex (the second column) in x-y plane at t/τ₀ = 5.0, 10.0 and 15.0, respectively. The third column shows the phase distribution of the vortex. The points A, B, C in (b) correspond to the times t/τ₀ = 5.0, 10.0, 15.0 in (d).

We have also studied the storage and retrieval of vortices for m = 2. The numerical result shows that these vortices are unstable during the propagation and hence a robust storage and retrieval of them are not available.

Discussion

From the results described above, a robust SLR for the (3 + 1)D weak-light bullets and vortices is possible by using the cold Λ-type three-level atomic system. These results can be easily generalized to other types of EIT systems with different (such as ladder-type⁸) level configurations. Furthermore, our theory can also be used to study the (3 + 1)D LSR with a Raman scheme^20,21, which has been suggested to obtain a broadband quantum memory of linear light pulses and has been realized recently by experiment by using the atomic ensemble working at room temperature^22,23.

In conclusion, we have proposed an EIT-based new scheme to realize a robust LSR for (3 + 1)D light pulses in a coherent atomic ensemble. Based on MB equations we have derived a nonlinear equation controlling the evolution of the probe-field envelope. We have shown that it is possible to obtain (3 + 1)D light bullets and vortices, which have very slow propagating velocity and ultra low generation power. We have further shown that these high-dimensional light pulses can be stabilized by using the balance between dispersion, diffraction, nonlinearity and by a Stark laser field. We have demonstrated that these high-dimensional light pulses can be stored and retrieved very stably by switching off and on a control field. Our study raise the possibility of guiding a related experiment and have potential applications in the area of light and quantum information processing.

Methods

Maxell-Bloch equations

In our semi-classical approach, MB equations are used to describe the motion of light field and atoms. Explicit expressions of the Bloch equation in the interaction picture are

where . Dephasing rates are defined as with being the spontaneous emission rate from the state |j〉 to all lower energy states |i〉 and being the dephasing rate reflecting the loss of phase coherence between |j〉 and |l〉.

Asymptotic expansion

Assume , with , and . Thus , with and . Here is the dimensionless small parameter characterizing the typical amplitude of the probe pulse. To obtain a divergence-free expansion, all the quantities on the right-hand side of the expansion are considered as functions of the multi-scale variables , , and . Substituting the expansions into Eqs. (1) and (2) and comparing the coefficients of , we obtain a set of linear but inhomogeneous equations which can be solved order by order.

The first order (q = 1) solution is given by and , where D = |Ω_c|² − (ω + Δ₂ + iγ₂₁)(ω + Δ₃ + iγ₃₁) and θ = K(ω)z₀ − ωt₀. The linear dispersion relation reads K(ω) = ω/c + κ₁₃(ω + Δ₂ + iγ₂₁)/D. F is a yet to be determined envelope function depending on the slow variables x₁, y₁, t₁, z₁ and z₂.

At the second order (q = 2), a solvability condition gives i[∂F/∂z₁ + (∂K/∂ω)∂F/∂t₁] = 0, with V_g = (∂K/∂ω)⁻¹. The approximation solution at this order reads , , and , where

and , with .

At the third order (q = 3), a solvability condition yields the equation (3). The explicit expressions of the self- and cross-phase modulation coefficients W₁₁ and W₁₂ are given by