Message spreading in networks with stickiness and persistence: Large clustering does not always facilitate large-scale diffusion

Abstract

Recent empirical studies have confirmed the key roles of complex contagion mechanisms such as memory, social reinforcement and decay effects in information diffusion and behavior spreading. Inspired by this fact, we here propose a new agent–based model to capture the whole picture of the joint action of the three mechanisms in information spreading, by quantifying the complex contagion mechanisms as stickiness and persistence and carry out extensive simulations of the model on various networks. By numerical simulations as well as theoretical analysis, we find that the stickiness of the message determines the critical dynamics of message diffusion on tree-like networks, whereas the persistence plays a decisive role on dense regular lattices. In either network, the greater persistence can effectively make the message more invasive. Of particular interest is that our research results renew our previous knowledge that messages can spread broader in networks with large clustering, which turns out to be only true when they can inform a non-zero fraction of the population in the limit of large system size.

Introduction

Over the last few years, many empirical works^{1,2,3,4,5,6,7} or practical model^8,9 have identified the strong relevance of complex contagion mechanisms such as memory effect, social reinforcement and decay effects to information diffusion or behavior spreading. On account of memory effect, the previous contact activities can affect the current spreading process^4,10. Specifically, individual's selection of message items can be naturally expedited by the increasing frequencies of the same choices of other people if they find the items interesting or crucial enough^3,8,11. This is usually interpreted as the results of social reinforcement^9,12,13. On the other hand, there are an increasing amount of new messages an individual is facing every day in modern real life, whereas the attention and processing abilities of people are finite and saturated^4,11,14. The novelty of a message usually trend to fade with time and hence the attention people pay to it, which is normally described as decay effects^1,4,11,15. It is shown that the social reinforcement effect could be weakened or even counterbalanced by decay effects^4,5,11.

Although the competition between social reinforcement and decay effects has been emphasized and used as a guideline to measure the natural time scale that attention fades away¹¹, to our best knowledge few works have been attempted to model explicitly the competition and memory effect and study deeply how it shapes the spreading of information on complex networks. Here we want to point out that the three mentioned effects in information spreading are quite different from those have been considered in the studies on Naming Game (NG) and Category Game (CG), since either NG or CG is a two-step multi-state negotiation process^16,17,18,19, whereas information spreading is not. First, herein memory effect performs as the storing of the times of contact of people with recipients of information^3,8, rather than the possible words (or names) for the object (or a category) in NG (or CG)^16,17,18,19. Second, decay effect in information spreading reflects the decay of people's interest or attention in a message owing to the competition with other news or stories^4,11, contrary to the NG (CG) in which it means the decrease of the number of different words used in the system (or average number of words per category)^16,17,18,19. Third, unlike the phenomenon that an hearing would have more opportunities to add (or remain) one word only if more selected speakers try to transmit the same one to it^16,17,18,19, the reinforcement effect in information diffusion indicates the more simple situation that the more neighbors adopting the message, the higher likelihood an individual following them^3,5.

Next, the big challenge we are confronted with is the possibility of modeling and studying the message spreading along with both social reinforcement and decay effects based on the memory effect. Recent researches⁶ have shown that the variation in the ways that different information spread is attributed to not only the stickiness – the probability of information adoption is mainly dominated by the first few exposures^6,7, but also the persistence – the relative extent to which more repeated exposures to the message continue to have durative effect. Similar results especially the exposure response behaviors were also confirmed by a lot of empirical studies^4,5,7. The two mechanisms, stickiness and persistence, thus enable us to quantitatively study the joint action of the three effects together.

At the same time, the structures of complex social systems can be characterized by complex networks, on which many spreading activities may take place, ranging from the spreading of epidemics^20,21,22,23, the diffusion of behaviors and news^3,8, to the promotion of technique innovations²⁴, etc. Consequently, motivated by the empirical studies^{3,4,5,6,7,8,11} mentioned above, we propose a new agent-based model offering an opportunity to explore the impact of social reinforcement and decaying effects quantified by stickiness and persistence on the message (information) diffusion on various networks. In the presence of strong decay effects, we find that a message is more likely to outbreak (i.e., it can reach a non-zero fraction of the population in the thermodynamic limit) on the tree-like networks such as scale-free (SF) networks and Erdős-Rényi (ER) random networks rather than on the regular lattices (RLs). Specifically, a message can spread broader in the RLs than that in the tree-like networks only if it can outbreak. The critical behaviors of the diffusion process can be reasonably estimated by the bond-percolation theory considering spatial correlations of the underlying networks through which message diffuses. In addition, we develop a verification approximation, whose solutions confirm well the non-negligible role of the dynamical correlations between transmission events in the RLs.

Results

Here, we first carry out extensive simulations for the agent-based model of message diffusion on square lattice. We then compare the simulation results with the predictions from the analytical bond percolation theory and verification method involving time correlations of the spreading events. Finally we extend our model and analytical methods to other networks such as RLs, SF networks and ER networks to validate the robustness of our findings.

Message diffusion on square lattice

We first consider the message diffusion on a square lattice of size N = L × L with periodic boundary conditions. The message starts spreading from the center node (selected as the seed), while all the others are in the susceptible state (i.e., they hear nothing about the message).

To intuitively grasp the roles of stickiness and persistence, we begin by presenting the time evolution of spatial patterns of message spreading in Fig. 1. The message with stickiness a = 0.40 (see the Methods for the precise definitions of a, b and other parameters) spreads in an irregular manner (see Fig. 1(a1)). By comparison, the message with a slightly stronger stickiness a = 0.45 diffuses outward to susceptible areas in a quasi-circular manner with a broader rim of informed (infected) individuals (see Fig. 1(a2)). This indicates that messages with different strength of stickiness could give rise quite different spreading patterns and behaviors. Figs. 1(b1) (b2) and Supplementary Fig. S1 show that the persistence b also affects considerably the whole spreading size, by governing the number of the isolated susceptible islands (blue domains surrounded by red areas, the emergence of these islands arises from the fact that continually increasing number of infected neighbors fail to infect those individuals owing to small persistence). The above arguments suggest that the stickiness and persistence have great but different influences on the spreading of message.

Figure 1

The time evolution of spatial patterns, for two different values of stickiness (a1) a = 0.40, (a2) a = 0.45 (bottom panel) where b = 0; and for two values of persistence (b1) b = −1.00, (b2) b = 1.00 (bottom panel) where a = 0.45.

Red sites represent recovered or alerted nodes, bright green sites represent infected ones and blue sites denote susceptible nodes. Other parameters are chosen as n_s = 2 and N = 101 × 101.

We next explore the critical behaviors of message diffusion for various stickiness and persistence, by providing a quantitative assessment of the message burstiness. By means of the theory of non-equilibrium phase transition in statistical physics which has been successfully generalized to study the epidemic dynamics, previous studies^25,26 on spreading dynamics have shown that the fluctuation of the order parameter is divergent at the critical point. We thus use the procedure proposed in²⁶ to numerically determine the critical areas. To be more specific, a series of variabilities v(a, b) are firstly obtained as

where ρ_R and v(a, b) denote, respectively, the density of recovered individuals in the population and the relative standard deviation (RSD) at parameter point (a, b). There exists a maximum variability v_max(b) for each value of b when varying a from 0 to 0.5 and the values of v_max(b) with b ∈ [−1, 1] can be used as the numerical estimation of the threshold position.

Although a bond-percolation process can be mapped to the SIR model^27,28, its extension to the current model is not straightforward. First, in our model, the transmission probability that a susceptible individual approves the message varies with the times he has received it from his infected neighbors (i.e., the number of informed neighbor he has had). Second, the time correlations between different transmission events E_n²⁷ (the transmission event E_n(t) represents that an individual, who has received the message at least once before, successfully approves the message when he has received it another n times until time t). To confirm the existence of the time correlation, in Fig. 2 we compare the dynamic proportions of the four transmission events () obtained from numerical simulations with those predicted by the bond percolation considering spatial correlations ( and see the Methods section for definitions of q_n and T_n(a, b)) for three parameter points (a, b). Here, ω_n(a, b, t) represents the occurrence frequency of E_n(t) obtained from numerical simulations and 〈k〉 denotes the average degree of the networks. In Figs. 2 (b) and (c), we see that α₀(t) (α₂(t)) is greater (less) than β₀(t) (β₂(t)) during the spreading process, whereas α₁(t) (α₃(t)) is equal or close to β₁(t) (β₃(t)). The reason is that the existence of time correlations of the transmission events E_n(t) can determine whether the subsequent events E_m(t) (m > n) happen or not in the spreading process. If E_n(t) does not happen, the events E_m(t) (m > n) will probably happen; otherwise E_m(t) (m > n) will never happen since an informed individual transmits the message only one time and then becomes recovered (i.e., completely ignores the message) forever. Consequently, E₀ (E₂) contributes more (less) than predicted by percolation theory to the spreading course (also see Supplementary Fig. S2). To overcome the challenge, we develop a verification approximation involving the time correlations of the transmission events, besides the spatial correlations originating from the spatial structure of the lattice²⁷. It is necessary to mention that the discrete-time synchronous transmission of the message enables us to avoid concerning about the additional synergistic effect²⁹. Moreover, Figs. 2(b) and (c) show that α_n(a, b, t) is dynamically stable, which shows that this correlation always exists. It allows us to adopt average values of the four indices α_n(a, b, t) at the critical regions for the verification approximation.

Figure 2

The evolution of proportions of the transmission events.

The parameters are chosen at (a) subcritical point a = 0.20, b = 0.20; (b) critical point a = 0.35, b = 0.20; and (c) supercritical point a = 0.43, b = 0.20.

Based on the proposed methods in the Methods section and Eq. (1), we yield both the analytical prediction and the verification threshold for n_s = 2, plus the numerical results for various n_s, as depicted in Fig. 3. We note that the numerical thresholds stay at a ≈ 0.32, which is mainly determined by the stickiness of message (i.e., the parameter a), regardless of the values of b and n_s. This means that most informed individuals are actually infected by their first one or two infected neighbors (also see Supplementary Figs. S2–S6). Furthermore, the numerical estimations are fairly reproduced by the bond-percolation theory. Comparing the analytical boundary, the verification approximation involving both spatial and time correlations gives a higher accurate estimation than the bond-percolation method considering only spatial correlations (the dashed black line is clearly closer to the numeric markers than the black solid line is).

Figure 3

The phase diagram of the message spreading.

The real numerical critical boundaries (crosses) are obtained by Eq. (1) for various n_s on square lattice of size N = 101 × 101. For comparison, analytical boundary (black line) and verification boundary (dash black line) for n_s = 2 are also shown (the cases for n_s = 3, 4, 5 do not allow us to analytically identify the critical lines). Herein, we select a narrow parameter ranges b ∈ [−1, 1] and a ∈ [0.32, 0.36] containing the numerical critical boundary for the calculation of verification threshold (see more detailed method in the Methods section).

Message diffusion on regular lattice networks and regular random networks

Centola's work³ concludes that social behaviors can spread farther and faster across clustered-lattice networks than across corresponding regular random networks (RRNs), owing to the strong social reinforcement induced by clustered ties. RRNs are networks that all nodes have exactly the same degree while links are randomly distributed among nodes, avoiding self-connections and multiple connections. To check whether the findings by Centola are still fulfilled for information diffusion, we further investigate our model defined on the RLs (Hexagonal network and Moore network) and the RRNs.

To get a comparison, we present in Fig. 4 the differences of the final size of recovered population on the two networks with the same average degree. The blue areas characterize the parameter regions where the conclusion of Centola's experiment (that the information spreads farther across the RLs than across the corresponding RRNs) does not hold. The violation is attributed to the presence of strong decay effects (b < 0) in the vicinity of the critical regions. Specifically, the outbreaks of message can happen more easily in the RRNs than that in the RLs for negative persistence owing to that strong decay effects outcompetes the weak reinforcement effect (also see Supplementary Fig. S7, strong reinforcement effect (decay effects) is reflected by large stickiness and/or positive persistence (negative persistence) in our model). As a and b get larger, things turn out differently, the message is able to seize a larger population in the RLs, which is accordant with the anticipation of Centola's experiment. This means that high level of clustering created by redundant ties that linked each node's neighbors to one another in the RLs strengthens the reinforcement effect and hence facilitates the diffusion of the message³. Moreover, larger n_s improves the performance of stickiness in facilitating the message diffusion, making social reinforcement effects be the most prominent for the RLs. Consequently, the blue areas shrink with increasing n_s. Thus, the above differences investigated indicate that network topology and n_s (which can be regarded as one of the intrinsic characteristics of the message) simultaneously determine the effects of stickiness and persistence on the spreading dynamics.

Figure 4

The differences of spreading sizes between RLs and RRNs networks (ρ_RL − ρ_RRN).

(a,b) n_s = 2, (c,d) n_s = 3. The average degrees of the networks are 〈k〉 = 6 (a,c) and 〈k〉 = 8 (b,d), respectively. ρ_RL (ρ_RRN) represents the recovered density of population (i.e., spreading size) on RLs (RRNs).

Using Eq. (1), we obtain the numerical thresholds for various values of n_s. According to the methods described in the Methods section, we can yield the analytical (theoretical) thresholds of message diffusion on both the RRNs and the RLs, in addition to the verification thresholds on the RLs for n_s = 2 (Supplementary Fig. S10 and Fig. 11 show that the time correlations between the transmission events in Hexagonal lattice and Moore lattice are noticeable). In the case of RRNs (Figs. 5(a) and (b)), we observe that the positions of the critical boundaries are mainly determined by both the stickiness and 〈k〉 instead of the persistence and n_s, on account of weaker social reinforcement^3,27 resulting from the low clustering coefficient. Unlike the case of RRNs, the theoretical analysis by means of bond-percolation theory gives rather accurate predications of the position of the threshold with strong persistence, but not for negative persistence (i.e, with the presence of strong decay effects) on the RLs. When the underlying networks for message diffusion are Hexagonal lattice and Moore lattice, more available edges for message spreading will further strengthen the role of persistence in message diffusion, especially with stronger social reinforcement (positive b). That enables all transmission events involve in the diffusion (see Supplementary Figs. S10–S13), so that β_n(a, b, t) gets close to α_n(a, b, t) (see Supplementary Figs. S10 and S11). On the other hand, the trajectories obtained by verification approximation are in good agreement with the simulations, from which one can conclude that the effect of time correlations of transmission events is indeed general on the RLs. Additionally, the message steps forward to arrive in half of the neighbors of the same host on the RLs by flowing through almost edges connecting it. This makes the message with positive persistence (b > 0) outbreak more easily in the presence of denser local connections and the persistence thus imposes a greater influence on outbreaks of message on RLs with larger average degree for small n_s (). The message also has reached a saturation state when the subsequent events E_i happen (see Supplementary Figs. S14–S21). Also in RLs, higher n_s limits the effect of persistence and the phase transitions are determined by not only the topologies of the networks but also the stickiness and persistence of the message.

Figure 5

The phase diagrams of the message spreading on RLs and RRNs.

The underlying networks are (a) RRN with 〈k〉 = 6, (b) RRN with 〈k〉 = 8, (c) Hexagonal lattice and (d) Moore lattice. The predictions from the bond-percolation theory (solid lines) and verification approximations (dashed lines) for n_s = 2 are illustrated to compare with the simulation data (markers) for various n_s. To get the verification trajectory on Hexagonal lattice (and Moore lattice), we select two parameter regions containing the numerical thresholds (see more detailed method in the Methods section). One region is b ∈ [−0.3, 1.0] and a ∈ [0.06, 0.24]; the other one is b ∈ [−0.3, 1.0] and a ∈ [0.01, 0.19] in Hexagonal lattice. One region is b ∈ [−1.0, −0.3] and a ∈ [0.23, 0.24]; the other one is b ∈ [−1.0, 0.3] and a ∈ [0.15, 0.18] in Moore lattice.

In addition, the reinforcement effect begins to work as the message is bursting and prevailing on both the RLs and RRNs. Therefore, the results for positive persistence near the thresholds (see Supplementary Figs. S12–S24) elucidate the actual phenomenon “Three men make a tiger” (or “A lie, if repeated often enough, will be accepted as truth”), where the majority do not believe the message as a truth until at least three neighbors have tried to transmit this message to them.

Message diffusion on SF networks and ER networks

To further check the robustness of our above findings, we finally investigate our message diffusion model on SF and ER networks with 〈k〉 = 6, 8, 10, 12. Since two or more transmission events fail to last over the long time at the critical points (see Supplementary Fig. S24), we do not take the time correlations into consideration in theoretical analysis. Compared with the simulation data, the analytical results for SF networks and ER networks with different average degrees show that the theoretical approaches are already sufficient to give fairly precise expressions of the outbreaks of message completely determined by the stickiness a (see Supplementary Fig. S25). Nevertheless, the persistence also partly boosts its impact on the size of message diffusion as 〈k〉 gets larger (see Supplementary Fig. S26).

Fig. 6 displays evident differences of the final spreading sizes on the RLs and SF (ER) networks with the same degree. The spreading sizes are larger in SF (ER) than those in the RLs at the parameter regions where the message has already outbroken on SF (ER) but not yet on the RLs, owing to the hubs and shorter shortest paths in SF (ER)³⁰ (see Supplementary Fig. S25 for the critical boundaries of message on SF and ER). Just for strong persistence, denser local connectivity of the RLs can make an invasion take place more easily. As a and b increase beyond the critical boundaries displayed in Fig. 5, the message can capture a larger population again on the RLs, despite of the existence of hubs the short characteristic path length in the SF (ER) networks. The reason is that very smaller clustering coefficient gives rise to weak social reinforcement effect^3,31, which again leads to weak performance of persistence in promoting the spread of message on the SF (ER) networks. Our results indicate that the role of reinforcement effect is more important than that of hubs or shortest paths in facilitating message spreading only when the message outbreaks on the RLs. Otherwise, especially for the presence of decay effects (negative persistence) the facilitation of hubs and shortest paths to the diffusion on SF (ER) cannot be neglected. In addition, the results for positive persistence on SF and ER networks can also be treated as evidence of the mechanism “Three men make a tiger” (see Supplementary Fig. S27 and Fig. S28).

Figure 6

The differences of spreading sizes between the RLs and SF (ER) networks (ρ_SF/ER − ρ_RL).

(a,b) the difference ρ_SF − ρ_RL, (c,d) the difference ρ_ER − ρ_RL. (a,c) The average degrees of the networks are 〈k〉 = 6 (a,c) and 〈k〉 = 8 (b,d), respectively. Here, ρ_SF (ρ_ER, ρ_RL) represents the recovered density in SF networks (ER networks, RLs). Other parameter: n_s = 2.

Discussion

In conclusion, taking into account social reinforcement and decay effects based on memory effect in reality, we have proposed a new agent-based message spreading model with stickiness and persistence and carried out extensive computer simulations of our model on various types of networks. By means of the relative standard deviation method and the bond percolation theory involving the spatial correlations, we are able to determine numerically and analytically the positions of critical boundaries. Moreover, the remarkable accuracy of verification approximation involving the time correlations between different transmission events validates the wide existence of such correlations for the message diffusion on regular lattices.

Our preliminary results show that in RLs, the persistence depends greatly on the position of inflection point n_s and average degree 〈k〉 of the underlying networks and begins to play a pivotal role in the spreading process with increasing 〈k〉 owning to the emergent large clustering coefficient³. Stronger social reinforcement arising from larger clustering coefficient leads readily to stronger infectivity of the message, which can invade a great number of susceptible individuals in the RLs, confirming the conclusion of Centola's work. By comparison, in tree-like networks such as RRNs, SF and ER, the critical thresholds of message diffusion are only dominated by the stickiness and both the hubs and the short characteristic path length facilitate the outbreaks of message in the presence of decay effects. It worth emphasizing that the results presented in this paper has successfully substantiated the phenomenon “Three men make a tiger” (or “A lie, if repeated often enough, will be accepted as truth”).

Placing our study in the context of social media, the hub nodes actually play a role of broadcasters, advertisements and so on, which are very important for the large scale spreading of information. However, the intrinsic contents of messages and their adaptation to hosts are extremely relevant in determining the message diffusion. In particular, the results for the message diffusion on the SF and ER networks constitute a proof that exposure to mass media can favour the outbreaks of behaviors, news or messages, despite the decay effects, only if the stickiness of the message is large enough. On the other hand, the RLs are efficient in taking advantage of social reinforcement effects to promote the global spreading of the message, owning to more cluster ties (or local pressures) that function as form of ‘initial groups’ or ‘small groups’ through interpersonal communication or ‘machine-interpersonal communication’³². It is also verified by our research that the local, personal communication is irreplaceable to lead to propagation of message despite of the developed media industry today, from the perspective of communication.

Recent studies have started considering the memory effect^3,8, social reinforcement and decay effects⁴ in information spreading. The mechanisms were yet investigated in isolation. Our work is the first attempt to account explicitly for the three key mechanisms together and to evaluate the joint action of them by quantifying their effects as stickiness and persistence. It provides a quantitative guideline for future social experiments for message spreading.

In reality, the ways in which information spread may be very complicated. In the present study, we do not capture the difference of individual-level preference³³ that might have also influenced their decisions to adopt one message. For example, in an online social network such as Twitter, individuals may prefer different hashtags and significant variations in the ways that the hashtags on different topics spread were observed⁷. In addition, one need to concern about the diverse cultural and societal backgrounds³⁴ which would lead to the different styles by which individuals contact with the medium, or even hamper communications among different groups of members³². Moreover, the volatilities of complex contagion of controversial topics, psychological status of individuals³⁵ reveal that the status of the individuals in the communication systems are time dependent, which should be addressed in future research.

Methods

Message spreading model with stickiness and persistence

The message spreading model is implemented on a network consisting of N nodes and E edges, where the nodes represent the individuals in a population and the edges the social interactions among them, through which information propagates. Each individual is allowed to be in one of three states at each time step: (i) Susceptible (or uninformed) state—the individual has not yet heard the message or is aware of the news but not willing to transmit it. (ii) Infected state—the individual catches the message and forwards it to all his nearest neighbors. (iii) Recovered state—the individual will never transmit the message any more after having transmitted it once before.

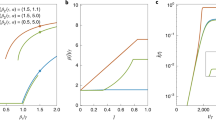
Specifically, the information propagation is modeled in a probabilistic framework at individual level^8,9. A susceptible individual i will adopt the message with a probability λ_n° (a, b), given that he has heard it from his informed neighbors n° times (i.e., n° informed neighbors he has had), plus the first time. In detail, n° = n + 1 when individual i has owned at least one informed neighbors, otherwise n° = 0. Here λ_n° (a, b) is a linear piecewise function of the times he has received message from his informed neighbors:

where k_i is the degree of node i. n_s is the inflection point beyond which persistence is the dominant factor for the infection probability of message and the parameters a (stickiness) and b (persistence) characterize how λ_n° (a, b) change with n°, as illustrated in Fig. 7. Since empirical data^3,6,7 have shown that social reinforcement sets in such that initial exposures generally increase infection probability, the parameter a should be non-negative when n° ≤ n_s. For n° > n_s, the competition between social reinforcement and decay effects, characterized by the parameter b, will be taken into account for the message adoption. If the reinforcement is strong enough the individual will be more likely to adopt the message with increasing n° (b > 0). Otherwise, even if many infected neighbors try to transmit the information to the focal individual i, the multiple exposures will lead to a decreased probability for the information adoption (b < 0). In the present study, we set b ∈ [−1, 1] and a ∈ (0, 0.5] so that the spreading dynamics of the message can be comprehensively investigated. For simplicity, we do not consider the diversity of individuals' response to the message and all individuals behave identically with the same values of parameters a and b.

Figure 7

The adopting probability of message as a function of n°.

The degree of stickiness and persistence are quantified as an_s and b, respectively. n_s denotes the position of inflection point.

We perform Monte Carlo (MC) simulations with synchronous updating of the states of all the individuals. Each MC step consists of the following three procedures: (i) All susceptible individuals decide whether or not to adopt the message with probability λ_n° (a, b); (ii) If an individual adopts the message, he will try to transmit what he has approved to all his nearest susceptible neighbors in the next step and then becomes recovered immediately; (iii) Otherwise, the susceptible individuals will wait to repeat the procedure (i) in the following MC steps. The above elementary spreading processes are repeated steps until there are no infected individuals anymore in the population.

Theoretical analysis of the model

For the occurrence probability of transmission event with τ = 1³⁶. We consider the spatial correlations that affect the process of diffusion, but do not yet influence the critical behaviour of the message spreading²⁷. The transition point from susceptible to infected phase is determined by^27,36

where 〈T〉 and T_C are, respectively, the mean transmissibility and the critical topology-dependent bond-percolation threshold. On the other hand, the mean transmissibility can be gotten as

where is the probability that the recipient has other n (n = 0, 1, 2, 3) infected neighbors except for the one chosen beforehand when considering the spatial correlations (p is the probability that one nearest neighbor of the focal individual is in infected state).

Combine Eqs. (2), (3), (4) and , the mean transmissibility for the discrete case reads as

Then we have

where , θ₁ = (1 − p)^〈k〉−1 and . The positive root is selected as the theoretical prediction

In SF networks, the critical point T_C beyond which the message can reach a finite faction of the population can be obtained³⁶ as . Since RRNs and ER networks are generated by connecting randomly selected pair of nodes, . Due to the randomness of connections in these networks, each edge of a neighbor of one host can probably connected to any other N − 2 individuals. Therefore, the transmission of message from an informed neighbor to the susceptible host (i.e., message flows through the edge in the system) will happen only if there is at least one infected individual in the left N − 2 ones to transmit the message to the recipient. In other words, the probability that the message flow can reach the susceptible host through the edges connecting to the recipient is for the three networks (i. e., the RRNs, SF networks and ER networks). Also, two or more transmission events fail to last over the long time at the critical points (see Supplementary Fig. S8, Fig. S9 and Figs. S25), so the time correlations are ruled out in the theoretical analysis for the cases of RRNs, SF networks and ER networks. In the regular lattices, since each one has exact 〈k〉 specific neighbors. Specifically, for square lattice with von Neumann neighborhood, for Hexagonal lattice and for the lattice with Moore neighborhood. The bond percolation threshold for a square lattice, T_C = 0.347 for Hexagonal lattice and T_C = 0.232 for square lattice with Moore neighborhood^27,37.

Verification approximation of information threshold

In analogous to q_n(a, b), we first set . According to Eq. (4), can be calculated numerically by counting the relative number of successful attacks (i.e, transmission events) α_n(a, b) from infected neighbors to hosts for given values of a and b and equating this to . In other words, α_n(a, b) represents numerically the proportion of E_n occurring at parameter point (a, b). Furthermore, can be normalized as

Q_n(a, b) actually represents the probability that the recipient owns n (n = 0, 1, 2, 3) infected neighbors expect for the preselected informed one, involving both the spatial and time correlations of the message diffusion.

Herein, we select different parameter regions containing the numerical critical boundaries for corresponding lattices with n_s = 2 for the calculation of Q_n(a, b). We average all non-zero Q_n(a, b) in the selected parameter ranges for the expected indices Q_n and substitute them into the equation

to get the verification thresholds.