Introduction

Quantum technology allows one to organize and control the components of a complex system governed by the laws of quantum physics1. Control lies at the heart of virtually every aspect of quantum science and in general it is very difficult to achieve. A retrospective and representative study of control follows the spin echo effect; inhomogeneous broadening of a spin can be removed by applying a single π inversion pulse halfway through the evolution2. Quantum control theory has matured over the last two decades, from single spin nuclear magnetic resonance experiments to large-scale manipulation during a quantum computation3. As long as quantum technology has room to grow, quantum control will remain an active area of research. It has already covered a lot of subjects, such as the Lie-algebraic conditions required for strong analytic controllability4,5,6, quantum feedback control on state preparation, stabilization or entanglement improvement7,8,9,10, time-dependent Hamiltonian designation for adiabatic passage11,12,13 and exact state transmission14,15,16,17. Every protocol mentioned before needs elaborate design.

After the investigations based on the control of closed quantum system18,19 were gradually extended into the open system regime20, active control sequences have been established to defeat the environmental dephasing and dissipation effects21,22,23,24,25. In light of the quantum Zeno effect or similar effects, decoherence of an open quantum system could be universally slowed down with ultra-fast modulation26,27,28 and concatenated pulses29. Many of these existing works are extremely relying on dynamical decoupling (DD) by subjecting the target system to a series of open-loop, high-frequency, control transformations30,31,32,33,34,35. DD and its varieties turn out to be a universal and efficient class of control method in both theory and experiments.

The control efficiency of DD, more precisely, the robustness of state fidelity under DD control against environment, is mainly determined by the ratio of the characteristic timescale of the environmental correlation function and the period or quasi-period of the pulses. In the Markov environment, we are faced with a vanishing correlation time. System control is almost impossible since any information contained within a quantum state will undertake irreversible loss due to the environment induced error before any external control comes into effect. Whereas in a non-Markovian environment, it is possible to drive a quantum state against the environmental influence with a properly configured control pulse sequence. A common approximation for DD and its varieties, such as UDD (Uhrig DD) and CDD (concatenated DD)31,32, invokes an ideal delta-function describing a zero-width pulse train with unbounded strength. It is essentially a perturbative approach to the effective Hamiltonian. In practice, realistic experiments can not be ideal: pulse strength is bounded, duration is finite and parametric fluctuations are inevitable. One can never completely eliminate stochastic quantum fluctuation and environmental noise from the laboratory. In other words, the DD mechanisms used in quantum control are generally not under total control themselves. In light of this consideration, we are prompted to answer the following question: to what extent can a pulse sequence with randomness be effective?

Traditional DD approaches break down when one discusses the errors randomly occurring in the pulse sequence. It is actually the zero-order approximation to a nonperburbative DD pulse sequence36. We will instead use a more realistic pulse description in the effective Hamiltonian consisting of all of the parameters, such as width, strength, pseudo-period and their fluctuations, which is based on the exact quantum-state-diffusion (QSD) equation [See Method].

Results

Random Control Model

An illustration of a regularly spaced rectangular wave train is shown in Fig. 1(a). This configuration allows us to parameterize experimental inaccuracies associated with the period τ, temporal duration Δ and strength Φ/Δ. A typical example of an imperfect or out-of-order rectangular pulse sequence is shown in Fig. 1(b). Notice the time-dependent strength, temporal duration and quasi-period in this case. We will use these parameters to measure the fault-tolerance of a system to pulse sequence inaccuracies. The regularly spaced sequence appearing in Fig. 1(a) should protect the quantum system from decoherence and relaxation. The robustness of our scheme can be portrayed by its fault-tolerance to fluctuations of three parameters. The quasi-period is defined as the time interval between the starting point of any pulse and that of its following pulse. The quasi-period will generally possess a random distribution. We can express these three fluctuating parameters as

where X = τ, Δ, Φ, respectively, DX's are their individual deviation scales and Rand(−1, 1) denotes a random number uniformly distributed between −1 and 1. This is a realistic noise model – stochastic fluctuations naturally occur within the quantum measurement devices and during the pulse creation process. In the limit of a large sample number, M[X′] = X, where M[·] denotes the statistical ensemble mean. Each random series is instantaneously generated and mutually independent. Furthermore, the random values are not shared between τ, Δ and Φ simultaneously. More importantly, they are unknown during our random control scheme. Without loss of generality, we require Δ + DΔ < τ − Dτ for each rectangular pulse to avoid unnecessary confusion.

Figure 1
figure 1

The diagrams of (a) perfect pulse sequence with constant distance, duration and strength and (b) irregular pulse sequence with random paramters.

Full size image

Fault-tolerant Control of Fidelity

Through the derivation by QSD equation [See Method]37,38,39, a qubit open system with Zeeman splitting ω embedded in a dissipative environment follows an exact stochastic Schrödinger equation driven by an effective Hamiltonian:

Here c(t) = Φ′/Δ′ during the “on” time of random pulse sequence which lasts Δ′ and subsequently c(t) = 0 during the “off” time of duration τ′ − Δ′ during an interval of instantaneous quasi-period τ′. Q(t) satisfies an ordinary differential equation and the boundary condition is Q(0) = 0. Γ and γ are parameters appearing in the correction function of environment . Γ is the system-environment coupling strength and 1/γ is proportional to the environmental memory time. When γ → ∞, the non-Markovian process is reduced to the Markov limit asymptotically.

For arbitrary initialization of the system |ψ0〉 = μ|1〉 + ν|0〉, |μ|2 + |ν|2 = 1, the fidelity that measures the survival probability can be expressed by:

where takes the real part of the following function. One can obtain the average of the fidelity over all possible pure state configurations and find

Below we will numerically examine the effects of random control on fidelity during time evolution.

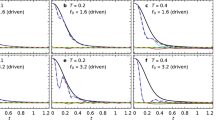
The efficiency of regular and random control is defined in terms of the time interval associated with a fidelity drop from unity to 0.95. The fidelity is functionally dependent on the bath memory coefficient γ. We illustrate the relationship between the memory function and the randomized DD parameters Φ, τ and Δ separately in Figs. 2, 3 and 4. Each calculation determines the randomization effects inherent to a specific control parameter while the remaining parameters remained fixed in a dummy state. The efficiency was then evaluated with respect to the ensemble average of these dummy states.

Figure 2
figure 2

The moment T when the average fidelity of a single qubit reduces to 0.95 from unity as a function of the fluctuation scale for pulse strength under different γ.

We choose Φ = 0.2ω, τ = 0.02ωt, Δ = 0.4τ and Γ = ω.

Full size image
Figure 3
figure 3

The moment T when the average fidelity of a single qubit reduces to 0.95 from unity as a function of the period fluctuation scale under different γ.

We choose Φ = 0.2ω, τ = 0.02ωt, Δ = 0.4τ and Γ = ω.

Full size image
Figure 4
figure 4

The moment T when the average fidelity of a single qubit reduces to 0.95 from unity as a function of the temporal duration fluctuation scale under different γ.

We choose Φ = 0.2ω, τ = 0.02ωt, Δ = 0.4τ and Γ = ω.

Full size image

The horizontal axes appearing in Figs. 2, 3 and 4 represent the ratio of the stochastic fluctuation scale DX to the mean value of the corresponding parameter X; X = Φ, τ and Δ, respectively. The fluctuations vanish at the origin of each of these coordinate systems. This is the condition for regular DD, hence, for a fixed γ, the relative efficiency of random and regular DD appears in reference to the intersection of the curve and the vertical axis. These results should also be compared to those which naturally emerge in the absence of control: , 0.87ωt and 0.65ωt when γ = 0.2, 0.5 and 0.9, respectively. Thus it is evident that both random and regular control greatly enhance the survival time of the target state as it evolves under open system dynamics; order-of-magnitude improvements are found even in the worst situations considered.

The efficiency has a varying sensitivity to deviations in the DD parameters. This behavior is illustrated in Figs. 2, 3 and 4. For example, deviations in the pulse strength hardly effect the value of . Deviations in the period of the pulse sequence have a small impact on the efficiency as well, though a modest decline in tends to occur with increasing Dτ/τ. However, the performance of the pulse sequence of DD becomes sensitive to deviations in Δ as the bath approaches the strong non-Markovian regime. This sensitivity is exemplified in Fig. 4 by the 40% reduction of T over the evaluation scale 5Δ/4 < τ′ < 15Δ/4 with γ = 0.2, a typical strong non-Markovian condition. These results indicate the effectiveness of noisy quantum DD. The relative performance of regular and random control depends on the environmental coefficient γ, improving as the environment becomes more Markovian. For near-Markovian processes, little distinction can be made between completely regular and completely random control.

The common thread among these three figures is the memory effect of the environment. In terms of the fidelity expression in Eq. (4), strong suppression of dissipation requires the exponential function to approach unity in the presence of c(t). In absence of control pulse,

where . A straightforward derivation shows that when γ is dominant in Eq (5), the absolute value of approximately decays in an exponential way with time. Thus the control pulse is not able to dynamically decouple the open system for dominantly large γ, i.e. within the near-Markovian environment. On the contrary, smaller γ implies a longer memory and a slower characteristic decay of the quantum state. Coherence can be preserved in this case with a control pulse of proper frequency. Appropriate pulse sequences could roughly wash out the dissipation influence. In summary, we have found that standard quantum DD can be quite effective when fluctuations occur in the pulse sequence. The performance is largely insensitive to fluctuations in pulse strength and sequence period. It is, however, quite sensitive to several other factors. The greatest influence, to no surprise, comes from the structure of the environmental noise process itself. A non-Markovian environment is required for effective DD in both cases, regular and random. Secondly, the control pulse sequence requires a sufficiently fast pulse series, i.e. a sufficiently small average value of τ. Dissipation effects from the system-environment interaction create disordered system dynamics, these effects can be neutralized if a sufficiently large number of control photons interact with the system during the characteristic correlation time of the environment. Hence, the required pulse rate depends on the fixed bath correlation time, a time that is inversely proportional to γ.

A third condition, which has not been discussed thus far, concerns the ratio between the pulse width and pulse periodicity. This dependence is clearly illustrated in Fig. 5 where comparisons in the fidelity evolution are made between regular and stochastic control for various Δ/τ. Perhaps the most striking comparison results when Δ/τ = 0.3 – random control can actually outperform regular control in some occasions. To be fair, we concede that regular DD is more favorable towards the beginning of this example evolution. As the interpulse separation diminishes, e.g. Δ = 0.75τ, it becomes difficult to discriminate the curves and the fidelity remains roughly the same in either case. Moreover, in Fig. 6, similar patterns emerge when we examine inter-parameter dependencies between Δ and τ. Both of these figures correspond to the same average Δ and τ. Again, we find examples where random control permits longer survival times than the regular case for long evolutionary periods. However, in this case random control outperforms regular DD control in early evolutionary intervals as well. Over the entire evaluation interval, random control yields a fidelity greater than 0.9 when the ratio between the average values of Δ and τ is optimized (Δ/τ ≥ 0.4). Although the optimized random controls yield slightly lower fidelities than the regular controls for these average values, they could adequately approximate the ideal regular sequence if the performance requirements are not prohibitively restrictive.

Figure 5
figure 5

The time evolution of the average fidelity of a single qubit under regular control (blue lines) and under random control (red lines) with different Δ.

We choose γ = 0.3, Φ = 0.2ω, τ = 0.02ωt and Γ = ω.

Full size image
Figure 6
figure 6

The time evolution of the average fidelity of a single qubit under regular control (blue lines) and under random control (red and gray lines) with different Δ, DΔ and Dτ.

We choose γ = 0.3, Φ = 0.2ω, τ = 0.02ωt and Γ = ω.

Full size image

Discussion

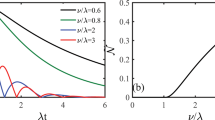
The effectiveness of the random DD pulse sequence is fairly state-independent. The similarity in performance for several initial qubit configurations is illustrated in Fig. 7. These configurations are defined in terms of the initial population |μ|2 of the upper level of the open qubit system. We plot the fidelity as a function of |μ|2 rather than μ in light of Eq. (3). Curves associated with a particular |μ|2 represent the common result of a group of quantum states with the same upper level population. We find a slight decrease in fidelity control efficiency with increasing |μ|2. Nevertheless, random control provides robust and reliable stabilization against damping effects for all possible initializations. In the short time regime, the efficiency of random control is nearly the same for every possible initial pure state.

Figure 7
figure 7

The time evolution of the fidelity of a single qubit under random control with different initial states indicated by population |μ|2.

We choose γ = 0.3, Φ = 0.2ω, τ = 0.02ωt, Δ = 0.4τ, DΔ = 0.2τ, Dτ = 0.2τ and Γ = ω.

Full size image

We have introduced a general unknown stochastic disturbance into the nonperturbative quantum DD model to account for imperfect laboratory control. An error-free control sequence consists of a sequence of identical, equally spaced pulses. In our nonperturbative method, this sequence has already far beyond the traditional DD pulse: the bang-bang (BB) control sequence. With high precision, we can control the average values of the parameters which characterize the sequence, but we cannot control the errors which occur on them or predict any occurrence in advance. Using the quantum-state-diffusion equation, we have analyzed the performance of a realistic quantum DD sequence prepared with random laboratory parametric fluctuations and find it to be effective in controlling the dynamics of an open quantum system over a wide range of non-Markovian processes.

The control efficiency, which is measured by the average fidelity over initial pure states, is found to be dependent on the average frequency of the control pulse, the environmental memory and the ratio of the average pulse duration time Δ to the period τ. When the mean values of Δ and τ are optimized into a very loose condition, random dynamical decoupling sequences can adequately approximate the ideal regular sequence if the performance requirements are not prohibitively restrictive. This will alleviate the experimental requirements placed on pulse sequence generation in quantum control to a great extent.

The survival time, which is measured by the time moment T when the system fidelity reduces to a given value from unity, is associated with the quantum speed limit (QSL) of open quantum systems40,41,42. The lower bound of the required time of evolution is , where 41. Kαs' are the Kraus operators characterizing the time evolution of the open system and ||A|| is the Hilbert-Schmidt norm of A. For our dissipation model, the summation in the expression of is , where the larger the population of the upper state is, the shorter the evolution time τ is. It can also be expected that if a system under a certain control yields nearly vanishing Q(t) during the evolution, τ could be very large such that T is greatly enhanced by the control. Although our system is in a non-Markovian environment, which is beyond the scope of Lindblad master equation, yet it turns out that when |μ|2 = 0.5 and there is no external control applied to the system, the survival time T corresponding to is around 0.13 (in the same unit as in Fig. 7), whereas the lower bound τ ≈ 0.05 which serves as a significant lower bound for T. In general, the QSL under non-Markovian dynamics and external dynamical control remains an interesting topic for future research.

The randomness considered here is entirely different from the random decoupling schemes initiated by L. Viola et al. (see Refs. 43,44,45). Based on standard (ideal) π pulse, the random DD proposed in these works allows the “control propagator” to follow a random but known path on the group of rotating operations. Both the past “control operations” and the moments at which they are applied are known, but the future “control path” is random. It should not be confused with the stochastic error considered in the phase or rotation axis of π pulse of DD, since by which the connection between the control efficiency and the randomly errors in shape of pulse is still not clear. Our DD with random control assumes the occurrence of unknown stochastic fluctuations over pulse sequence parameters, including duration time, period and strength. The magnitude of the errors or fluctuations are so big that the previous DD pulse sequence now has not much significance than a reference. This investigation also differs from the control with no control procedure proposed by some of the authors of this work, see Ref. 46. There, an out-of-control environment consisting of disordered external white noise was shown to suppress decoherence in a more ordered system. Here, we demonstrate the effectiveness of quantum state stabilization when irregular control pulses are applied.

Methods

We employ an exact stochastic Schrödinger equation, the QSD equation, to investigate this stochastic special DD process. This allows one to include the function of external pulse sequence directly into the microscopic quantum model. For an arbitrary model (setting [planck] = 1):

where and respectively denote the creation and annihilation operators for the k-th mode in the bosonic bath. In the interaction picture with respect to , an exact QSD equation generally reads37,38:

Here Hsys(t) is the system Hamiltonian that could absorb an arbitrary DD pulse function. We have dropped the ket notation for ψt(z*) ≡ |ψt(z*)〉. L is the coupling operator of the system with the environment. is the environmental Gaussion noise process satisfying and and G(t, s) is the environmental correlation function. includes system operators and the environmental noises with O-operator satisfying:

and O(s, s, z*) = L. The states ψt(z*) of the system correspond to a particular “configuration” z*, thus the system density matrix is recovered by ρt = M[|ψt(z*)〉 〈ψt(z*)|].

Consider the random control over a single two-level system (qubit) which is under the dissipative influence from the environment, so that Hsys = E(t)σz/2 and L = σ−. The non-perturbative pulse sequence indicated by a function of time c(t), regular or random, contributes to the system energy shift E(t) = ω + c(t). For this model, the exact effective Hamiltonian in Eq. (7) is found to be Eq. (2).