Extracting quantum dynamical resources: consumption of non-Markovianity for noise reduction

Abstract

A great many efforts are dedicated to developing noise reduction and mitigation methods. One remarkable achievement in this direction is dynamical decoupling (DD), although its applicability remains limited because fast control is required. Using resource theoretic tools, we show that non-Markovianity is a resource for noise reduction, raising the possibility that it can be leveraged for noise reduction where traditional DD methods fail. We propose a non-Markovian optimisation technique for finding DD pulses. Using a prototypical noise model, we numerically demonstrate that our optimisation-based methods are capable of drastically improving the exploitation of temporal correlations, extending the timescales at which noise suppression is viable by at least two orders of magnitude, compared to traditional DD which does not use any knowledge of the non-Markovian environment. Importantly, the corresponding tools are built on operational grounds and can be easily implemented to reduce noise in the current generation of quantum devices.

Introduction

Even the most promising platforms for quantum computing^1,2 are inherently plagued with complex quantum noise^3,4,5,6, which must be significantly reduced to meet the threshold required for error corrected quantum computing^7,8,9. This has led to a flurry of techniques for noise characterisation and control^10,11, including dynamical decoupling (DD)^{12,13,14,15,16,17,18,19}.

The goal of DD is to remove the interference from the environment to implement a desired dynamics. This is achieved by open-loop control, i.e. applying a fixed sequence of unitary interventions, which have the effect of cancelling the influence of the environment, somewhat analogously to how the rotation of a spinning top keeps it upright. However, the successful application of DD techniques on existing devices often requires faster control than is feasible. Still, it may be possible to loosen these limitations by devising DD schemes that cancel the influence of the environment in a more bespoke way, by accounting for the ability of the environment to carry a memory²⁰, a property known as non-Markovianity^6,21. This connection between noise suppression and quantum memory and its application to DD-like techniques has been conjectured but is still lacking a formal quantitative description^22,23.

In the search for a birdseye view of quantum control and noise mitigation techniques, we turn to the formalism of quantum resource theories²⁴, which has had tremendous success in quantifying the utility of properties like entanglement and coherence^25,26,27 as well as resources embedded within transformations^28,29,30,31. A quantum resource theory consists of a set of potential resource objects, and a set of free, i.e. implementable transformations on those resources. Using these transformations, one can partition the potential resource objects into: free resource objects that can be readily produced under the free transformations alone, and non-free ones which require the experimenter to have access to some additional ‘resourceful quantity’ to acquire. These resourceful quantities may be properties like entanglement and coherence, and are typically used to quantify the ability perform tasks like the production and distillation of arbitrary states^25,26, and communication³². They are quantified by resource monotones. When considering the usage of non-Markovianity for noise suppression, loosely speaking, the resource at hand is the memory present in the noise, while the free operations consist of the control that pulses that the experimenter can apply. However, to date, no resource theory currently exists for noise reduction—arguably one of the most important goals in quantum physics in the present era. The most similar task described by existing literature is the distillation of many noisy channels into fewer noiseless ones³³. While this is important in its own right, it cannot describe noise reduction on the entire system of interest, as is sought for DD.

We argue that the reason why a resource theoretic quantification of noise reduction techniques like DD does not yet exist, is that the necessary resource objects are multitime quantum processes, as opposed to states or channels used in the previous resource theory literature. This is because multitime correlations^34,35 are crucial to the efficacy of DD.

Recently, a resource theory of multitime processes³⁶ was built around the process tensor formalism^6,37, enabling multitime correlations to be probed and quantified using resource monotones. Alas even with multitime quantum process frameworks such as these, it seems like noise reduction is impossible, as it would explicitly involve making a resource object—the noisy process that is to be ‘de-noised’—more valuable under free transformations—something strictly forbidden in all resource theories.

Our innovation is to sidestep this apparent impossibility by concentrating resources in the temporally separated subsystems of a process’ multitime Choi state, analogously to how more traditional resource distillation concentrates resources held in spatially separated subsystems. Mathematically, this requires a notion of temporal coarse-graining for multitime processes, whose property of irreversibility accounts for how aptly chosen control at a short timescale translates to noise suppression at a long timescale. By introducing resource theories of temporal resolution (RTTR), we provide the mathematical framework which, through temporal coarse-graining, unifies channel and multitime resource theories, thus enabling a clear quantification of the resources needed for noise suppression, including but not limited to DD. In particular, closely aligned with DD we provide the resource theory of independent quantum instruments (IQI), a prototypical resource theory of temporal resolution for noise reduction.

Subsequently, we apply the tools of semi-definite optimisation to our process tensor formalism, to search for optimal DD sequences within the resource theory of IQI. This optimisation is informed by the specific non-Markovian correlations within a multitime process, whose characterisation is already known. Finally, the optimisation methods we present in this work are numerically demonstrated to produce a drastic lengthening in the timescales for noise suppression, as compared to traditional DD. Finally, the ‘noise-tailored’ optimisation methods we present in this work are numerically demonstrated to produce a drastic lengthening in the timescales for noise suppression when compared to traditional, noise-agnostic, DD. This result adds to the growing body of work towards minimising noise by characterising and harnessing the respective properties of the underlying noise process^{10,38,39,40,41}. Importantly, while resource theories have made great mathematical strides, their direct impact on quantum technologies has arguably been limited. Our results aim to provide concrete means to close this gap.

Results

A resource theory is a mathematical structure consisting of a set of potential resource objects, and a set of implementable free transformations upon those resource objects. From that starting point, one can deduce which resources are free, which are costly, and find monotones (i.e. functions that do not increase under free operations) that quantify the value of any given resource object. To translate this abstract formalism into a description of DD, there are two prerequisites. Firstly, noise processes must be cast as resources, and DD must be seen as transformations of those noise processes. Secondly, there must be a mechanism by which DD sequences can decrease noise under resource non-generating operations (i.e. those performable in DD setups). Below, the first issue is addressed using the process tensor framework, and the second is resolved by irreversibility of temporal coarse-graining. For a detailed summary of the notation we employ throughout this paper, see supplementary Table 1.

Physical scenario

Any quantum noise can be modelled as an evolution operator ${{{{\mathcal{T}}}}}_{t:0}^{{{{\rm{se}}}}}$ jointly acting on the system (s) of interest and its environment (e) for some time t. In order to minimise the formation of s-e correlations, DD applies control operations on s at n intermediate times. This divides the evolution ${{{{\mathcal{T}}}}}_{t:0}^{{{{\rm{se}}}}}$ into time segments $\hat{n}=\{{t}_{1},\ldots,{t}_{n}\}$. The resulting n step noise process on s then has a concise representation as a quantum comb⁴², also known as a process tensor ${{{{\bf{T}}}}}_{\hat{n}}$^6,37,43, consisting of sequences of s-e evolution maps

$${{{{\bf{T}}}}}_{\hat{n}}:= {{{{\rm{tr}}}}}_{{{{\rm{e}}}}}{\circ }_{e}{{{{\mathcal{T}}}}}_{t:{t}_{n}}^{{{{\rm{se}}}}}{\circ }_{e}\cdots {\circ }_{e}{{{{\mathcal{T}}}}}_{{t}_{1}:0}^{{{{\rm{se}}}}}{\circ }_{e}{\rho }_{0}^{{{{\rm{e}}}}},$$

(1)

where ${\rho }_{0}^{{{{\rm{e}}}}}$ is an initial environment state, and ${\circ }_{e}$ denotes composition on the e subsystem, of functions. In this notation, the partial trace and appending of states such as ${\rho }_{0}^{{{{\rm{e}}}}}$ are explicitly considered as functions to be composed over e, and ${{{{\bf{T}}}}}_{\hat{n}}$ is an object ‘with n open slots’ (see Fig. 1), i.e. it acts on n operations/interventions on the system.

Fig. 1: Dynamical decoupling of non-Markovian processes.

a To decouple a system from its environment, an experimenter interacts with the process ${{{{\bf{T}}}}}_{\hat{n}}$ (maroon) at intermediate times $\hat{n}=\{{t}_{1},\ldots,{t}_{n}\}$. This amounts to applying chosen control operations, and then temporally coarse-graining the process. When the experimenter chooses to do nothing (left), the resulting channel is ${{{{\bf{T}}}}}_{{{\emptyset}}}:= \left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\right]$. When they instead apply a traditional DD sequence (right) ${{{{\bf{A}}}}}_{\hat{n}}=\{{{{\mathcal{I}}}},{{{\mathcal{X}}}},{{{\mathcal{Z}}}},{{{\mathcal{X}}}},{{{\mathcal{Z}}}}\}$, the process is transformed as ${{{{\bf{T}}}}}_{\hat{n}}\mapsto {{{{\bf{T}}}}}_{\hat{n}}^{{\prime} }=\left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\right]$ (Eq. (3)), where ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}=\{{{{\mathcal{I}}}},{{{\mathcal{I}}}},{{{\mathcal{X}}}},{{{\mathcal{X}}}},{{{\mathcal{Y}}}},{{{\mathcal{Y}}}},{{{\mathcal{Z}}}},{{{\mathcal{Z}}}}\}$ such that ${{{{\bf{T}}}}}_{{{\emptyset}}}^{{\prime} }:= \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{\prime} }| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]=\left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}{{\emptyset}}}\right]\!\right]$ (Eq. (2)) has greater mutual information than ${{{{\bf{T}}}}}_{{{\emptyset}}}$. b Information about the system of interest s that flows into the environment e under a non-Markovian process is not necessarily lost. Instead, this information becomes increasingly `tangled' in a complex web of multitime correlations. c DD `untangles' these multitime correlations into correlations held in s alone, which in itself impedes the formation o f new s-e correlations in a Zeno-like manner. d Optimal dynamical decoupling (see Sec.II-G) performs this conversion of correlations more efficiently, resulting in better noise reduction over longer timescales compared to a traditional dynamical decoupling sequence.

${{{{\bf{T}}}}}_{\hat{n}}$ has a natural representation as a Choi matrix⁶ that lives on 2n + 2 copies of s, two per intermediate intervention and one for the initial input and final output, respectively. Importantly, ${{{{\bf{T}}}}}_{\hat{n}}$ incorporates all pertinent memory effects between different points in time^43,44 and is a completely positive and trace preserving transformation. In what follows, it will become apparant, that DD is simply a transformation of the noise process ${{{{\bf{T}}}}}_{\hat{n}}$ that ‘untangles’ complex multitime correlations in the process tensor—mediated by e—such that the temporal correlations are isolated to s alone, i.e. information is preserved. We depict this in Fig. 1.

Concretely, exercising any control over this process ${{{{\bf{T}}}}}_{\hat{n}}$, including a DD sequence, amounts to contraction of the above tensor with an analogous control tensor ${{{{\bf{A}}}}}_{\hat{n}}$ acting at intermediate times $\hat{n}$. The set of control operations is broad and may include physical pulses as well as logical gates, depending on the experimental scenario. We require that these experimental interventions be performed at a timescale much faster than that of the noise process. While this is a good approximation in most relevant scenarios (where the control Hamiltonian is much stronger than the noise Hamiltonian), a breakdown of this assumption would prevent the required separation of experimenter and environment influences. We note that the assumption of brief interventions is common to most DD techniques, and discrete-time control more generally. The contraction of the noise process with control sequence is denoted by

$${{{{\bf{T}}}}}_{{{\emptyset}}}^{{\prime} }:= \left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{A}}}}}_{\hat{n}}\right]\!\right].$$

(2)

Here, the process tensor is on the left and the control tensor is on the right by convention—see panel (a) of Fig. 1 for a depiction and Sec. IC-A for details of our compact notation for tensor contractions. A specific detail of importance is that the control sequence is taken to include pre- and post- operations to the whole dynamics, meaning that it has two spaces that will not contract with the process in Eq. (2). Consequently, ${{{{\bf{T}}}}}_{{{\emptyset}}}^{{\prime} }$ is simply a familiar quantum channel (not a scalar), where the set of intermediate times is the empty set.

Resource theories for quantum processes

We now bring in the tools of resource theories of multitime processes³⁶ to uncover the resources of ${{{{\bf{T}}}}}_{\hat{n}}$ that allow for dynamical decoupling. Any resource theory comprises of resource objects and transformation on these objects. Here, noise processes ${{{{\bf{T}}}}}_{\hat{n}}$ are the resource objects, while experimental control transforms one process into another. To formalise this idea we introduce superprocesses ${{{{\bf{Z}}}}}_{\hat{n}\hat{m}}$ that map n intervention processes to m intervention processes³⁶

$${{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }=\left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{m}}\right]\!\right].$$

(3)

Here, the tensor contraction notation from Eq. (2) is extended to denote transforming one process into another with an operator ${{{{\bf{Z}}}}}_{\hat{n}\hat{m}}$, see Fig. 1. Physically, this latter superprocess consists of pre- and post- processing operations on the s and additional ancillary system a, see Sec. Representation of Free Transformations for more details. Just as the operations within ${{{{\bf{A}}}}}_{\hat{n}}$ were taken to be effectively instantaneous, so are those of ${{{{\bf{Z}}}}}_{\hat{n}\hat{m}}$. For n = 0, i.e. the case of channels ${{{{\bf{T}}}}}_{{{\emptyset}}}$ the corresponding superprocess ${{{{\bf{Z}}}}}_{{{\emptyset}}{{\emptyset}}}$ (mapping channels to channels) is called a supermap and has been widely studied^{28,29,30,33,45}. In general, the superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{m}}$ is a rather flexible object that transforms processes on n times to processes on m times. To connect these abstract objects to physically relevant scenarios and to reveal the underlying mechanism of DD and similar noise reduction methods, it is necessary to break this transformation into two less general objects. The first is a superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ that does not change the temporal structure (in the sense that it leaves the number of times for interventions invariant). The second is temporal coarse-graining which only changes the temporal structure, i.e. reduces the accessibility of the underlying process to the experimenter. This—at first glance artificial—two-step decomposition of superprocesses allows for the identification, quantification and utilisation of resources for noise reduction, as we demonstrate for DD.

A resource theory of multitime processes—defined by a set of readily available free processes and the set of implementable free superprocesses—provides a framework to describe how noise processes can be manipulated. It naturally gives rise to a set of monotones and resources²⁴, i.e. non-increasing functions of the process under the action of free superprocess (which are determined by the respective experimental control). One such resource that has been identified in some of these theories³⁶ is non-Markovianity. Our goal now is to quantify the role of non-Markovian memory in protocols like DD. However, ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$, the superprocesses which DD employs, are resource preserving or decreasing transformations in the sense that they cannot increase the non-Markovianity of a given process ${{{{\bf{T}}}}}_{\hat{n}}$. In fact, since ideal DD pulses are unitary, the non-Markovianity of a process will be the same before and after a DD superprocess ${{{{\bf{T}}}}}_{\hat{n}}\mapsto {{{{\bf{T}}}}}_{\hat{n}}^{{\prime} }$. As alluded to above, It turns out that we need one more ingredient for successful noise mitigation; we will show that DD consumes multitime correlations under our two-part temporal coarse-graining procedure, which is shown in Fig. 3a. In this light, the goal of DD is to find an optimal superprocess such that the two-part coarse-graining procedure most efficiently harnesses multitime non-Markovian correlations to produce correlations at the system-level.

Temporal coarse-graining

Specifically, the goal is to transform a noisy process ${{{{\bf{T}}}}}_{\hat{n}}$ into a clean quantum channel ${{{{\bf{T}}}}}_{{{\emptyset}}}^{{\prime} }$. To accomplish this, one must first apply a superprocess that yields the transformed (n-step) process ${{{{\bf{T}}}}}_{\hat{n}}^{{\prime} }$ and then transform it to a channel ${{{{\bf{T}}}}}_{{{\emptyset}}}^{{\prime} }$ via temporal coarse-graining, see the bottom two lines of Fig. 3a for a graphical depiction. The latter consists of removing times available for intermediate interventions by applying n − m identity maps ${{{{\mathcal{I}}}}}_{i}^{{{{\rm{s}}}}}$. We denote this operation corresponding to coarse-graining all but $\hat{m}$ times by ${{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}$, where identities are applied to all times in $\hat{n}$ that are not also in $\hat{m}$. Thus, for $\hat{m}\subseteq \hat{n}$, we can re-express Eq. (3) as

$${{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }=\left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{m}}\right]\!\right]=\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right].$$

(4)

Here, ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ maps between process tensors of the same type, while ${{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}$ can be seen as temporal coarse-graining from an n intervention process to a m intervention process with $\hat{m}\subseteq \hat{n}$.

The benefit of this two-tiered view point is that all non-trivial allowed control can be delegated to the free superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$, whose purpose in noise reduction is to rearrange temporal correlations such that the noise is destructively canceled upon subsequent coarse-graining. This, in turn, concentrates the system-level temporal correlations, a procedure that can be thought of as analogous to resource distillation, where some resource is concentrated among fewer spatially distinct subsystems^33,46. Here, the concentration of resources is temporal, rather than spatial.

Noise reduction is possible because of the irreversibility of temporal coarse-graining, see Sec. Proof of Obs.

Observation 1

(Irreversibility of temporal coarse-graining) Temporal coarse-graining ${{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}:{{\mathsf{T}}}_{\hat{n}}\to {{\mathsf{T}}}_{\hat{m}}$ is an order reflecting operation. This is that for all processes ${{{{\bf{T}}}}}_{\hat{n}}$ and $\hat{m}\subseteq \hat{n}$

$$\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]=:{{{{\bf{T}}}}}_{\hat{m}}\mathop{\mapsto }\limits^{{{{{\bf{Z}}}}}_{\hat{m}\hat{m}}}{{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }\,\,\,\,\Rightarrow \,\,\,\,{{{{\bf{T}}}}}_{\hat{n}}\mathop{\mapsto }\limits^{{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}{{{{\bf{T}}}}}_{\hat{n}}^{{\prime} },$$

(5)

where ${{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }:= \left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{\prime} }| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\right]$. However, the converse of Eq. (5)—known as the order preserving property—is not true in general.

Eq. (5) simply means that if a transformation is possible by means of free superprocesses ${{{{\bf{Z}}}}}_{\hat{m}\hat{m}}$ from the coarse-grained perspective, its corresponding fine grained transformation must also be possible via some free superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$. Importantly, the converse of Eq. (5) is false in general, meaning that one is always better off in the fine-grained picture than the coarse one. Concretely, for every ${{{{\bf{Z}}}}}_{\hat{m}\hat{m}}$, there exists an ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$, such that ${{{{\bf{Z}}}}}_{\hat{m}\hat{m}}={{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\circ {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$, but not every ${{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\circ {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ corresponds to a free superproess ${{{{\bf{Z}}}}}_{\hat{m}\hat{m}}$, see Fig. 2. When specifically concerned with the task of information preservation, a stronger version of this statement holds (Thm. 2 in Sec. Irreversibility Leads to Perceived Non-Monotonicity): noise reduction is possible if and only if having fine-grained access enables higher monotone values to be achieved. In Sec. Noise Reduction Monotones and Sec. Multitimescale Optimal Dynamical Decoupling we use the quantum relative entropy to show that the efficacy of protocols like DD is directly related to the consumption of non-Markovian correlations. Due to the scaling of relative entropy with the dimension of its arguments —which coarse-graining reduces—temporal resolution is almost always a resource for noise reduction, going far beyond any specific DD protocol. Crucially however, not all processes will be amenable to DD (e.g. depolarising noise) regardless of how rapidly the experimenter can act. This is why it is necessary to identify other resources that can help with DD, like non-Markovianity.

Fig. 2: Irreversibility of temporal coarse-graining.

(Left) Temporal coarse-graining transitions between levels of temporal accessibility/resolution to the same underlying process: from fine resolution to coarse resolution. (Right) This transition is inherently irreversible, as described in Obs. 1. Fewer transformations are possible after performing temporal coarse-graining than before. Explicitly, given a process ${{{{\bf{T}}}}}_{\hat{n}}$, one can immediately coarse-grain to ${{{{\bf{T}}}}}_{\hat{m}}$ (m ≤ n), or first apply a superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ to obtain ${{{{\bf{T}}}}}_{\hat{n}}^{{\prime} }$, which is subsequently coarse-grained to ${{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }$. From this perspective, noise reduction occurs when the application of ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ resulted in ${{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }$ having greater mutual information between its intputs and outputs compared to ${{{{\bf{T}}}}}_{\hat{m}}$.

Resource theories of temporal resolution

Throughout, we will choose the input-output correlations of the resulting channel as a measure of success of noise reduction. On the other hand, the resources used to obtain that success are a property of the underlying multitime process. The addition of temporal coarse-graining allows the gap between channel resources and multitime resources to be bridged, creating a resource theory that can compare processes interacted with at any number of times. We call these resource theories of temporal resolution (RTTR), in reference to the inherent value of being able to intervene at more times. Shown in Fig. 3a, a RTTR is obtained by combining superprocesses and temporal coarse-graining, including the possibility to convert multitime processes into channels.

Fig. 3: Resource theories and noise reduction.

The relationship between resource theories of temporal resolution and noise reduction methods. a Resource objects are noise processes ${{{{\bf{T}}}}}_{\hat{n}}$, and free transformations can be represented as a superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$, followed by temporal coarse-graining ${{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}$, i.e. ${{{{\bf{T}}}}}_{\hat{n}}\mapsto {{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }:= \left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\right]$. The diagram shows three intermediate interventions at times $\hat{n}=\{{t}_{1},{t}_{2},{t}_{3}\}$ where the superprocess is `plugged in', followed by full coarse-graining, i.e. $\hat{m}={{\emptyset}}$. The properties of the noise process are encoded in the ${{{\mathcal{T}}}}$ channels constituting ${{{{\bf{T}}}}}_{\hat{n}}$, while the capabilities of the experimenter are specified by the form and connectivity of the ${{{\mathcal{V}}}}$ (pre) and ${{{\mathcal{W}}}}$ (post) channels of ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$. b The relationship between the properties of ${{{{\bf{T}}}}}_{\hat{n}}$, the respective free superprocesses which specify the RTTR, and the type of information a technique achievable within that resource theory can preserve. All techniques listed here can be performed by an experimenter possessing the full abilities of IQI. Restricting the superprocesses to a sub-theory of independent unitaries (IU), DD harnesses non-Markovian noise to preserve a full quantum state. Restricting control to sequences of repeated unitaries (RU ⊂ IU) the inducement of a decoherence free subspace (DFS) harnesses symmetries to preserve a subspace. Both quantum error correction (QEC) and the quantum Zeno effect (QZE) can in principle be performed for any kind of noise, but the extra ability of IQI over the independent entanglement breaking (IEB) theory means that QEC can preserve a full quantum state, rather than just classical information. See Sec. DISCUSSION and the Supplementary Discussion for more details.

Definition 1

(RTTR). A resource theory of temporal resolution consists of a set T of potential processes ${{{{\bf{T}}}}}_{\hat{n}}$ with any non-negative integer $n\in {{\mathbb{Z}}}_{\ge 0}$ of intermediate times, and a set Z of free transformations ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$, containing both experimentally implementable superprocesses, and temporal coarse-graining, of the form ${{{{\bf{Z}}}}}_{\hat{n}\hat{m}}=\left[\!\!\left[{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]$ for any $\hat{m}\subseteq \hat{n}$ (see Lem. 1). The free set of transformations Z is associated with a set T^F of free processes, which can be obtained for free.

In Fig. 3b, we visualise how properties of an underling process can be harnessed in a given RTTR, corresponding to a particular noise reduction technique, preserving some desired subset of information. This naturally reflects the fact that RTTRs differ in the free operations they allow for, corresponding to what can ‘easily’ be implemented in a considered experimental situation.

To study the task of noise reduction we introduce a prototypical RTTR—the resource theory of independent quantum instruments (IQI)—that allows any pre-determined, memoryless sequence of quantum operations at times $\hat{m}\,,\,{{\emptyset}}\subseteq \hat{m}\subseteq \hat{n}$. This resource theory encompasses DD as well as other important noise reduction methods like quantum error correction (QEC). The free superprocesses in IQI contain arbitrary quantum operations, but allow no memory, i.e. the action taken at one step cannot depend in an adaptive way on that taken at a previous step. For fixed numbers of times, superprocesses following this structure have been recently explored within the resource theory $({{\emptyset}},{{{\mathscr{Q}}}})$, where ${{\emptyset}}$ denotes the absence of memory and ${{{\mathscr{Q}}}}$ comprises all possible time-local experimental interventions³⁶. Also, observe that the only processes which can be produced in IQI for free, consist of independent channels that cannot convey any information. In this resource theory, the problem of noise reduction can be framed as finding an appropriate sequence of manipulations on the system, such that after coarse-graining the information retained is maximised.

Noise reduction monotones

Noise reduction can be roughly viewed as the task of maximising the information that a process can transmit. Naturally then, the monotones in a resource theory describing noise reduction should be ones that quantify various classes of temporal correlations, which is indeed what we find for IQI. Treating the Choi state of a process ${{{{\bf{T}}}}}_{\hat{n}}$ as its fundamental descriptor, it is possible quantify its temporal correlations by considering two types of marginal states:

$${{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}\,:= \mathop{\bigotimes }\limits_{j=1}^{n+1}{{{{\rm{tr}}}}}_{\bar{j}}\{{{{{\bf{T}}}}}_{\hat{n}}\}\quad \,{{\mbox{and}}}\,\quad {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\,:= \,\,\,\mathop{\bigotimes}\limits_{k=1}^{2(n+1)}\,\,{{{{\rm{tr}}}}}_{\bar{k}}\{{{{{\bf{T}}}}}_{\hat{n}}\}.$$

(6)

The index j enumerates the constituent channels ${{{{\mathcal{T}}}}}_{j}$ as in Eq. (1), and k splits this further into the inputs and outputs of those channels. The overline on an index signifies its complement. Consequently, ${{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}$ only contains the Markovian (i.e. between neighbouring times) temporal correlations of ${{{{\bf{T}}}}}_{\hat{n}}$, while ${{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}$ contains no temporal correlations whatsoever. These processes act as references with respect to which the quantum relative entropy $S(x\parallel y):= \,{{\mbox{tr}}}\,\{x\log (x)-x\log (y)\}$ compares the original process ${{{{\bf{T}}}}}_{\hat{n}}$ against. In IQI, we thus define three functions: the total information I, non-Markovianity N, and Markovian information M,

$$\begin{array}{ll}&I({{{{\bf{T}}}}}_{\hat{n}})\,:= \,S\left({{{{\bf{T}}}}}_{\hat{n}}\parallel {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\right),\,\,N({{{{\bf{T}}}}}_{\hat{n}})\,:= \,S\left({{{{\bf{T}}}}}_{\hat{n}}\parallel {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}\right),\\ &\,{{\mbox{and}}}\,\,\,M({{{{\bf{T}}}}}_{\hat{n}}):= S\left({{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}\parallel {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\right).\end{array}$$

(7)

All three of these functions are resource monotones in IQI.

Theorem 1

(I, N, and M are Monotones of IQI). Total mutual information I, non-Markovianity N, and Markovian information M, as defined in Eq. (7), are monotonic under the free transformations of IQI.

Proof

Monotonicity under the free superprocesses of IQI is established in Prop. 1, in the Methods Sec. Monotonicity of I, M, N under Free Superprocesses of IQI, while monotonicity under temporal coarse-graining is outlined in Methods Sec. Contractivity of Relative Entropy Under Coarse-Grainings, and proved formally in the Supplementary Methods ⬜.

Importantly, the total temporal correlations I are attributable to either N—corresponding to memory due to interactions with the environment—or M—corresponding to the capability to transmit information between adjacent times,

$$I({{{{\bf{T}}}}}_{\hat{n}})=M({{{{\bf{T}}}}}_{\hat{n}})+N({{{{\bf{T}}}}}_{\hat{n}}).$$

(8)

See Sec. Derivation of Eq. (8), for a proof of this equality. Hence, the trade-off between Markovian and non-Markovian correlations is a ‘zero-sum game’. As it turns out, the aim of DD is to increase M potentially at the expense of N. However, there are still additional complexities that must be addressed.

Decoupling mechanisms

Due to monotonicity, all quantities in Eq. (8) can only shrink under free transformations. However, since these quantities scale with the dimension of the Choi state—which shrinks under coarse graining—it is possible to produce a post-transformation process ${{{{\bf{T}}}}}_{\hat{m}}^{{\prime} }:= \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}^{{{{\rm{DD}}}}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]$ which maximises M, e.g. a sequence of identity channels, or some other sequence of unitaries in the ideal case. In order to maximise M, the non-Markovianity N of the resultant process must be minimised. Importantly, this is a resource distillation task, but resources are concentrated amongst temporally distinct subsystems rather than spatially distinct ones. The temporal nature of the distillation task explains why DD in particular can be performed on the entire system of interest, while other noise reduction methods like quantum error correction only preserve the logical qubits encoded by a larger number of physical qubits.

This effect can also be compounded by a well established Zeno-like effect^47,48, where the rate of formation of system-environment correlations (i.e. noise) is proportional to the amount already present, which fast DD pulses keep low. However, when working with slow pulses, DD cannot benefit from this effect, and its efficacy reduces. However, DD methods that harness the non-Markovian correlations of the noise may not be as constrained by pulse rapidity requirements.

Multitimescale optimal dynamical decoupling

The success of noise suppression techniques can be quantified by measuring I in the resultant process tensor after applying a superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ (e.g. ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}^{{{{\rm{DD}}}}}$ for traditional DD), followed by coarse-graining

$${I}_{\hat{m}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}({{{{\bf{T}}}}}_{\hat{n}}):= I({{{{\bf{T}}}}}_{\hat{m}}^{{\prime} })=I\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]\right).$$

(9)

In general, I > M and further DD may be possible at the coarser timescale defined by $\hat{m}$. However, when $\hat{m}={{\emptyset}}$, the mutual information of the channel defined in Eq. (2) is recovered, I = M holds, and no further DD is possible. Naturally, the important figure of merit to gauge the success of a decoupling scheme is the comparison between the standard decoupling scheme ${I}_{\hat{m}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}^{{{{\rm{DD}}}}}}$, and the case where no decoupling scheme is applied: ${I}_{\hat{m}}({{{{\bf{T}}}}}_{\hat{n}}):= I\left(\left[\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\right]\right)$.

Using this understanding of DD, the question of finding the best noise suppression method amounts to finding a control sequence ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$, such that ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}$ is maximised. To achieve this goal, i.e. to numerically find an ‘ideal’ control sequence we employ an algorithm which we call optimal dynamical decoupling (ODD) (see Secs. Numerical Optimisation and IV-J for details on (M)ODD) involving see-saw semidefinite program (SDP)⁴⁹ optimisation to find an optimal pulse sequence for specific process tensors, numerically demonstrating that a more efficient consumption of N results in a greater preservation of I – even at long timescales where traditional DD fails.

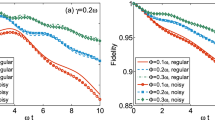
We test this resource theoretic characterisation of DD using a prototypical model (see Sec. Dynamical Decoupling Technique and Numerical Model for details), comparing the three cases ${I}_{{{\emptyset}}}$, ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}^{{{{\rm{DD}}}}}}$, and ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}^{{{{\rm{ODD}}}}}}$. Our first result is to optimally decouple four evolutions, i.e. the earliest quarter of the evolution depicted in Fig. 4a. Figure 4b shows that ODD achieves significant noise reduction over standard DD, especially at long timescales, suggesting that the advantage of ODD is caused by a more efficient consumption of non-Markovianity, which is not necessarily dependent on rapid pulses. This advantage can also be attributed to the additional requirement of knowledge of the process tensor, which traditional DD does not require.

Fig. 4: Numerical study of noise reduction.

All evolutions last a duration Δt. The data is averaged 20 different process tensors and smoothed in the time domain to average over oscillatory behaviour, and a 2σ confidence interval about the mean is shaded. a A process with 15 intermediate times has either no control applied Ref, (traditional) DD, CDD, ODD, or MODD. ${{{{\mathcal{A}}}}}_{i}$ are optimised at the short timescale, and ${{{{\mathcal{B}}}}}_{i}$ are optimised after coarse-graining. b Effectiveness at preserving channel-level information ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}$ and ${I}_{{{\emptyset}}}$ for the first 3 intermediate interventions of (a). A single period of traditional DD slows the loss of information by roughly one order of magnitude in Δt, while ODD is effective for the whole range of Δt values tested. c Effectiveness at preserving channel-level information ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}$ and ${I}_{{{\emptyset}}}$ for the full duration. CDD shows a marginal improvement over traditional DD. Both are significantly outperformed by ODD, which comes close to saturating mutual information for the whole set of Δt values. Finally, MODD, obtains a small improvement over the already near-ideal result of ODD. d Changes in monotones, e.g. ${{\Delta }}I={I}_{\hat{m}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}({{{{\bf{T}}}}}_{\hat{n}})-{I}_{\hat{m}}({{{{\bf{T}}}}}_{\hat{n}})$, after coarse-graining from n = 15 intermediate interventions to m = 3, minus before that coarse-graining. For both traditional DD and MODD, N is always lower with the protocol than without (ΔN is negative), indicating a conversion of non-Markovian correlations N to system-level correlations M, resulting in an increase in I as well. The sharp decline in the effectiveness of traditional DD in (c) begins at the peak in (d), suggesting that traditional DD loses effectiveness when it can no longer convert between N and M.

Now considering the entire duration of 16 evolutions depicted Fig. 4a, the dimension of the corresponding Choi state of the full process is too large to feasibly perform the process characterisation, nor the pulse optimisation required for ODD without approximation. Thus, we expand upon the ODD technique by breaking this process into smaller segments and iterate ODD over each of them sequentially (see Alg. 1 setting C = 1, i.e. the optimisation occurs at one timescale). The results on Fig. 4c show that this iterative ODD method remains highly effective at long times, while traditional DD does not.

Yet, there are still more resources remaining untapped. Once we find n pulses through this iterative method, we may coarse-grain to a longer timescale and optimise the resultant process again. This concatenation process can be repeated to optimise over arbitrarily long timescales, while incurring little additional computational cost. We call this layered approach multitimescale optimal dynamical decoupling (MODD), which is related in spirit to concatenated dynamical decoupling (CDD)⁵⁰. The core steps of MODD are outlined in Alg. 1. In our simulations we optimise at two different timescales, corresponding to a value of C = 2 in Alg. 1. This is achieved by coarse-graining from 16 evolutions to 4 during the optimisation. Figure 4c shows that, while iterative ODD (MODD at a single timescale C = 1) is able to preserve most of information in a process, optimising at an additional coarser timescale (C = 2) allows for further gains.

In Fig. 4d one can see the difference in each of our monotones before and after the applied control plus coarse-graining 16 evolutions into 4 evolutions: ΔN, ΔM, and ΔI. When the change ΔN is negative, we observe corresponding positive changes for ΔI and ΔM. We associate this behaviour with a consumption of non-Markovianity resources that were present in the initial process, but not in the final process. For the standard DD procedure at long timescales, it is visible that this behaviour breaks down; non-Markovianity no longer decreases, and neither the total nor the Markovian mutual information increase. However, MODD is capable of retaining this negative ΔN, and the corresponding positive ΔI and ΔM for for significantly longer timescales.

Numerical optimisation

We begin by outlining MODD in full generality.

Algorithm 1

MODD

The goal of Alg. 1 is to find an optimal DD sequence that accounts for non-Markovian effects. Since process tensor characterisation scales exponentially with the number of times considered, numerous approximations are required to achieve this goal. However, given these approximations, the complexity of process characterisation and optimisation required for MODD scales linearly with n.

Firstly, Alg. 1 breaks the (potentially) untractably large full process tensor on n times into computable m < n-time segments and finds optimal pulse sequences for each segment. It optimises from the earliest segment to the latest segment, using the pulses found for earlier segments to produce subsequent segments, thus accounting for potential non-Markovian effects. This leads a good—albeit not necessarily optimal—guess for a length-n decoupling sequence. Both to increase optimality, and to make use of potential long-scale memory effects MODD can work from the finest available timescale to the coarsest, via iterating temporal coarse-graining with the optimisation procedure. Overall, this exploitation of short-term memory effects (via ODD of the individual segments) and long-term memory effects (by leaving open slots and optimising them in the end) yields more optimal decoupling sequences than mere a mere repetition of the ODD sequences obtained for a single segment of length m, and we expect it to significantly outperform ODD whenever long-scale memory plays a non-negligible role.

We emphasise that this procedure necessitates the maximisation of ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{{\hat{m}}_{j}^{i}{\hat{m}}_{j}^{i}}}$ for a given process tensor ${{{{\bf{T}}}}}_{{\hat{m}}_{j}^{i}}$ (Line 6 in Alg. 1). Concretely, it requires a solution of the following problem:

$$\begin{array}{rll}{{{\bf{given}}}} & {{{{\bf{T}}}}}_{{\hat{m}}_{j}^{i}}\\ {{{\bf{maximize}}}} & {I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{{\hat{m}}_{j}^{i}{\hat{m}}_{j}^{i}}}({{{{\bf{T}}}}}_{{\hat{m}}_{j}^{i}}):= I\left(\left[\!\!\left[{{{{\bf{T}}}}}_{{\hat{m}}_{j}^{i}}| {{{{\bf{Z}}}}}_{{\hat{m}}_{j}^{i}{\hat{m}}_{j}^{i}}| {{{{\bf{I}}}}}_{{\hat{m}}_{j}^{i}}\right]\!\!\right]\right)\\ {{{\bf{subject}}}}\,\,{{{\bf{to}}}} & \left.\left.{{{{\bf{Z}}}}}_{{\hat{m}}_{j}^{i}{\hat{m}}_{j}^{i}}| {{{{\bf{I}}}}}_{{\hat{m}}_{j}^{i}}\right]\!\!\right]=\left.\left.| {{{{\mathcal{A}}}}}_{1}\otimes \cdots \otimes {{{{\mathcal{A}}}}}_{{m}_{j}^{i}}\right]\!\!\right]\,,\\ &{{{{\mathcal{A}}}}}_{1},\ldots,{{{{\mathcal{A}}}}}_{{m}_{j}^{i}}\,\,{{{\rm{are}}}}\,{{{\rm{CPTP}}}}.\end{array}$$

(10)

That is, one aims to maximise the mutual information between input and output by optimising the CPTP maps ${{{{\mathcal{A}}}}}_{k}$ applied at times t_k. However, this problem is neither linear nor convex with respect to the variables ${{{{\mathcal{A}}}}}_{k}$, nor is the mutual information a quantity that is amenable to simple direct numerical optimisation techniques. To overcome the latter problem, we instead optimise a proxy of the mutual information, namely the largest eigenvalue of the Choi matrix of the resulting channel. Analogously, to re-establish convexity and linearity, we do not optimise over the CPTP maps ${{{{\mathcal{A}}}}}_{1},\ldots,{{{{\mathcal{A}}}}}_{{m}_{j}^{i}}$ concurrently, but iteratively. This is achieved via a see-saw semidefinite program (SDP), which can be solved numerically efficiently. The details of this numerical procedure can be found in Sec. Dynamical Decoupling Technique and Numerical Model. Evidently, making the problem amenable to simple numerical optimisation techniques comes with the draw-back that one is not guaranteed to converge to a global maximum of the mutual information between input and output. However, the approach we choose suffices for our purposes since it already demonstrates the consumption of resources in DD that we discuss above, and indeed finds control sequences that vastly outperform the traditional DD sequences (see Fig. 4b).

Discussion

Given the results we present, what conclusions can be drawn about non-Markovianity and noise reduction? It is an established trend that as the environment starts to behave in a Markovian manner, noise reduction via DD becomes more difficult. However, non-Markovianity is not necessary for noise reduction, as our counterexample in the Supplementary Discussion shows. Nor does it appear that the presence of non-Markovianity is sufficient for DD to take place, as suggested by Ref. ²². The mere consumption of non-Markovianity does not imply that noise is being reduced either (consider a superprocess consisting of uncorrelated ‘junk’ operations). Despite these complexities, our results allow us to draw an unambiguous conclusion. Thm. 1 implies that non-Markovianity is a resource for noise reduction in a strict mathematical sense, and our numerical results shown in Fig. 4 suggest that methods that efficiently leverage this resource correspond to improved performance at noise reduction, when compared to DD methods that make no assumptions about the noise process.

Contrasted with many other DD methods, (M)ODD requires knowledge of the process tensor. Consequently, the observed advantage of (M)ODD over standard periodic and DD and CDD can be attributed to the value of this extra knowledge. Given this, it is important to study how the performance of (M)ODD compares to other techniques that assume knowledge of the environment. Uhrig dynamical decoupling was originally conceived as an optimal pulse sequence to preserve a qubit coupled to a bosonic bath⁵¹. Moreover, locally optimised DD⁵² and optimised bandwidth adapted DD⁵³ both go a step further to assume explicit knowledge of the spectral density of the noise, which makes them more similar (at least in spirit) to our methods. Interestingly, Ref. ⁵³ found the two latter methods significantly outperformed Uhrig dynamical decoupling, demonstrating the value of this type of knowledge. There are also other more recent attempts to optimise noise reduction based on the characterisation of classical noise⁵⁴. It will be an important topic of future research to see how noise reduction based on a fully quantum characterisation of the non-Markovian process compares to these existing methods.

The applicability of RTTRs to noise suppression is not limited to DD; even just within the constraints of IQI it is also possible to implement the quantum Zeno effect (QZE), decoherence free subspaces (DFS), and most importantly quantum error correction (QEC). The sub-theory structure of IQI is summarised in panel (b) of Fig. 3, and a more detailed discussion can be found in the Supplementary Discussion.

QEC requires syndrome measurements and conditional re-preparations^8,9—which are contained in IQI but are not unitary. Hence, QEC can be studied within the scope of IQI, but not the more restricted theory of independent unitaries (IU), which is sufficient for DD. QEC can be seen as a kind of (spatial) resource distillation task, in that a large number of noisy physical qubits are used to encode a small number of fault-tolerant logical qubits. Since both DD and QEC are encapsulated within IQI, we expect that resource theoretic tools can be brought to bear on hybrid DD/QEC techniques^55,56, concentrating resources among both spatially and temporally distinct subsystems, for further improved noise reduction.

Conversely, inducing a DFS^13,57 requires only the repetition of a single unitary, rather than a sequence of different unitaries, meaning that it can be implemented under a stricter theory of repeated unitaries RU ⊂ IU ⊂ IQI, where no clock-like memory of which pulses to apply is allowed. Rather than non-Markovianity, this harnesses symmetries in the system-environment interaction. Again, nothing precludes a technique harnessesing both jointly. Finally, the quantum Zeno effect (QZE)⁵⁸ can be cast as the RTTR of independent entanglement breaking (operations) IEB ⊂ IQI, where the repeated action is a measurement rather than a unitary, and one can still preserve classical information.

The concrete link between a process’ amenability to DD and its non-Markovianity has long been an elusive problem. In reconciling these two properties, we have constructed a flexible resource theoretic framework whose scope extends significantly beyond just DD. Complex multitime processes can be characterised as resource objects, their resource content can be quantified with entropy monotones, and resource transformations corresponding to optimised noise reduction can be applied via (M)ODD. Our numerical results show that significant resources remain untapped via traditional DD methods. Thus, extracting these untapped dynamical resources has the potential to greatly extend the domain of applicability of noise reduction techniques in the current generation of NISQ devices.

Doing so will require characterisation of the noise process, which has recently been achieved on a commercial-grade device¹⁰, and refined in Refs. ^38,59. Moreover, Refs. ^10,38,39 used the characterisation information for noise reduction, which is a variant of optimal dynamical decoupling. We note that our methods for (M)ODD, mitigate scalability concerns associated with the characterisation of many-step processes. Additionally, Ref. ⁶⁰ has compared a collection of the most prominent DD methods in the literature on IBM quantum computers, and found that the results were device specific, emphasising the importance of tailoring DD to the specific hardware in question. A practical further step towards the goal of improving DD, is to combine our (M)ODD methods with optimisation of pulse spacing.

Interestingly, the resource theoretic approach to DD opens the question of whether a useful bound on noise reduction may exist. Already, our monotone I induces such a bound, but that bound is not tight, since relative entropy scales with the dimension of its argument. If such a bound can be found, characterisation of the (correlated) noise on a quantum device would already provide the fundamental efficiency limits of any noise reduction method.

A promising way forward towards an identification of such fundamental bounds is the construction of a resource theory that is similar to IQI, but is convex. IQI can be seen as a prototypical resource theory for noise reduction, since it identifies all temporal correlations as resources. However, we expect that some correlations can be ignored on physically justifiable grounds, such that a bound on noise reduction can be derived for that theory. Moreover, since the experimenter in that theory would be more powerful than the one in IQI, such a bound would be valid here too.

Methods

The Methods section of this paper is arranged as follows. We begin with an explanation of the employed tensor contraction notation. Next we show that coarse-graining is indeed irreversible, and provide an interpretation in terms of monotones. After this we outline a proof of the contractivity of relative entropy under temporal coarse-graining (which is given in its entirety in the Supplementary Methods). This is necessary for I, M, and N to be monotones in IQI. Next, we show that I, M, and N are all individually monotones in IQI, and prove that I can be partitioned into M + N. The final section provides a description of the numerical model and optimisation method used for the results of Fig. 4.

Also, see the Supplementary Discussion for a detailed discussion of the parallel and sequential product structure of these theories, as well as the sub-theory structure of IQI. The Supplementary Discussion also contains a discussion of the Markovianisation of noise via dynamical decoupling, and a summary of the notation used throughout this text.

Tensor contraction notation

It is convenient when working with process tensors, superprocesses, and control sequences/coarse-graining, to have a shorthand notation that expresses how these objects fit together. For this, we use a tensor contraction, which always reduces the dimensionality of its inputs, but does not necessarily return a scalar. This contraction is written in a bra-ket style

$$\left[\!\!\left[{{{{\bf{A}}}}}_{\hat{{{{\rm{a}}}}}}| {{{{\bf{B}}}}}_{\hat{{{{\rm{a}}}}}\hat{b}}\right]\!\!\right]={{{{\bf{C}}}}}_{\hat{b}},$$

(11)

where ${{{{\bf{A}}}}}_{\hat{{{{\rm{a}}}}}}$ is a process tensor with intermediate times $\hat{{{{\rm{a}}}}}$, and ${{{{\bf{B}}}}}_{\hat{{{{\rm{a}}}}}\hat{b}}$ is a control sequence (or coarse-graining) on $\hat{{{{\rm{a}}}}}$ and $\hat{b}$ that removes all times in (or, graphically, all slots corresponding to) $\hat{{{{\rm{a}}}}}\setminus \hat{b}$. Consequently, the output object ${{{{\bf{C}}}}}_{\hat{b}}$ in the above equation has intermediate times $\hat{b}$. In this paper, $\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus {{\emptyset}}}\right]\!\!\right]:= \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]$ yields a channel (i.e. a process ‘without slots’), since channels are what we use to measure noise reduction. This notation for tensor contractions can be turned into an inner product (in the sense that it yields a scalar) by adding an initial state preparation and taking the control sequence to include a measurement on the final Hilbert space of the process tensor; the corresponding output scalar then corresponds to the measurement statistics. However, throughout we mostly deal with contractions to processes with fewer slots, or full contractions to channels (not scalars).

We point out that the link product⁴² would also be an appropriate choice of notation, but for our purposes our notation is tailored to highlight the dual action of superprocesses in a way that is analogous to the dual action of operators in bra-ket notation. We will see this shortly below.

Translating traditional superoperator notation to ours, the action of a process tensor on a control sequence is

$${{{{\bf{T}}}}}_{\hat{n}}[{{{{\bf{A}}}}}_{\hat{n}}]:= \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{A}}}}}_{\hat{n}}\right]\!\!\right]={{{{\rm{tr}}}}}_{{{{\rm{int}}}}}\left\{{{{{\bf{T}}}}}_{\hat{n}}{{{{\bf{A}}}}}_{\hat{n}}^{T}\right\},$$

(12)

where T is the transpose, ‘int’ corresponds to all intermediate spaces between the initial input and final output spaces. For generality, ${{{{\bf{A}}}}}_{\hat{n}}$ is taken to include pre- and post-processing operations on these input and output spaces at times 0 and t respectively. The action of a superprocess on a process tensor is

$${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}[{{{{\bf{T}}}}}_{\hat{n}}]:= \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]={{{{\rm{tr}}}}}_{{{{\rm{upper}}}}}\left\{{{{{\bf{T}}}}}_{\hat{n}}{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}^{{T}_{{{{\rm{upper}}}}}}\right\},$$

(13)

where the ‘upper’ index denotes the Hilbert spaces on the upper half of the superprocess, which join to the process tensor as in Fig. 3. The full trio of objects is

$$\left({{{{\bf{Z}}}}}_{\hat{n}\hat{n}}[{{{{\bf{T}}}}}_{\hat{n}}]\right)[{{{{\bf{A}}}}}_{\hat{n}}]:= \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{A}}}}}_{\hat{n}}\right]\!\!\right].$$

(14)

Superprocesses have a dual action which in this notation behaves much like how operators behave in bra-ket notation

$${{{{\bf{T}}}}}_{{{\emptyset}}}=\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{\prime} }| {{{{\bf{A}}}}}_{\hat{n}}\right]\!\!\right]=\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{A}}}}}_{\hat{n}}\right]\!\right]=\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{A}}}}}_{\hat{n}}^{{\prime} }\right]\!\!\right].$$

(15)

Note that when an object is on its own, as the resultant channel ${{{{\bf{T}}}}}_{{{\emptyset}}}$ is in Eq. (15), we omit the square brackets.

Representation of free transformations

Here, we provide a simple representation of all transformations in RTTRs, which will be used to prove the irreversibility of coarse graining (i.e. Obs. 1). To this end, we define a RTTR S = (T, Z) where T is the set of potential processes for any non-negative integer $n\in {{\mathbb{Z}}}_{\ge 0}$ of intermediate times, and Z are the free transformations (both superprocesses and coarse-grainings).

Superprocesses consist of pre- and post-processing operations to the s part of each evolution map in Eq. (1):

$${{{{\mathcal{T}}}}}_{{t}_{j}:{t}_{j-1}}^{{{{\rm{se}}}}}\mapsto {{{{\mathcal{T}}}}}_{{t}_{j}:{t}_{j-1}}^{{\prime} {{{\rm{se}}}}}:= {{{{\mathcal{V}}}}}_{\alpha }^{{{{\rm{sa}}}}}{\circ }_{{{{\rm{sa}}}}}{{{{\mathcal{T}}}}}_{{t}_{j}:{t}_{j-1}}^{{{{\rm{se}}}}}{\circ }_{{{{\rm{sa}}}}}{{{{\mathcal{W}}}}}_{\alpha }^{{{{\rm{sa}}}}}.$$

(16)

The superprocess may potentially make use of additional ancillary system a. The form and connectivity of ${{{{\mathcal{V}}}}}_{\alpha }^{{{{\rm{sa}}}}}$ and ${{{{\mathcal{W}}}}}_{\alpha }^{{{{\rm{sa}}}}}$ correspond to experimental constraints (which in turn define what tasks can be completed, see Fig. 1 for more details). The other kind of free transformation in a RTTR is temporal coarse-graining which does nothing other than removing times available for intermediate interventions. For an arbitrary process ${{{{\bf{T}}}}}_{\hat{n}}$ with a set $\hat{n}$ of times for intermediate interventions, temporal coarse-graining to m < n times is achieved by n − m identity maps ${{{{\mathcal{I}}}}}_{i}^{{{{\rm{s}}}}}$ on the system s

$${{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}:= \mathop{\otimes }\limits_{i\in \hat{n}\setminus \hat{m}}{{{{\mathcal{I}}}}}_{i}^{{{{\rm{s}}}}}\quad \,{{\mbox{for}}}\,\quad {{\emptyset}}\subseteq \hat{m}\subseteq \hat{n}.$$

(17)

The free-ness of temporal coarse-graining can be simply seen as a consequence of the fact that choosing to do nothing is free. Hence, it is possible to combine these two kinds of free transformations into a fully general joint transformation.

Lemma 1

Given a resource theory of temporal resolution S, all free transformations can be represented as

$${{{{\bf{Z}}}}}_{\hat{n}\hat{m}}=\left[\!\!\left[{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right].$$

(18)

Proof

A sequence of transformations in a resource theory of temporal resolution can be written explicitly as

$$\left[\!\!\left[{{{{\bf{Z}}}}}_{\hat{z}\hat{z}}| {{{{\bf{I}}}}}_{\hat{z}\setminus \hat{y}}\right]\!\!\right]\left[\!\!\left[{{{{\bf{Z}}}}}_{\hat{y}\hat{y}}| {{{{\bf{I}}}}}_{\hat{y}\setminus \hat{x}}\right]\!\!\right]\ldots \left[\!\!\left[{{{{\bf{Z}}}}}_{\hat{b}\hat{b}}| {{{{\bf{I}}}}}_{\hat{b}\setminus \hat{{{{\rm{a}}}}}}\right]\!\!\right],$$

(19)

with $\hat{z}\supseteq \cdots \supseteq \hat{{{{\rm{a}}}}}$. For any level of coarse-graining $\hat{\beta }$ there exists a fine grained view of the underlying process such that $\hat{\alpha }\supseteq \hat{\beta }$ such that any ${{{{\bf{Z}}}}}_{\hat{\beta }\hat{\beta }}$ can be expressed as ${{{{\bf{Z}}}}}_{\hat{\beta }\hat{\beta }}:= \left[\!\!\left[{{{{\bf{I}}}}}_{\hat{\alpha }\setminus \hat{\beta }}| {{{{\bf{Z}}}}}_{\hat{\alpha }\hat{\alpha }}| {{{{\bf{I}}}}}_{\hat{\alpha }\setminus \hat{\beta }}\right]\!\!\right]$ for some fine grained superprocess ${{{{\bf{Z}}}}}_{\hat{\alpha }\hat{\alpha }}$. This is possible because we allow the identity, i.e. ‘do nothing’ action to be free within the resource theory. As such, the actions of ${{{{\bf{Z}}}}}_{\hat{\alpha }\hat{\alpha }}$ at times $\hat{\alpha }\setminus \hat{\beta }$ are identities, ensuring that the fine and coarse pictures are physically equivalent. Hence Eq. (19) can be re-written as

$$\left[\!\!\left[{{{{\bf{Z}}}}}_{\hat{z}\hat{z}}| {{{{\bf{Z}}}}}_{\hat{z}\hat{z}}^{y}| \ldots | {{{{\bf{Z}}}}}_{\hat{z}\hat{z}}^{{{{\rm{a}}}}}| {{{{\bf{I}}}}}_{\hat{z}\setminus \hat{{{{\rm{a}}}}}}\right]\!\!\right]:= \left[\!\!\left[{{{{\bf{Z}}}}}_{\hat{z}\hat{z}}^{{\prime} }| {{{{\bf{I}}}}}_{\hat{z}\setminus \hat{{{{\rm{a}}}}}}\right]\!\!\right],$$

(20)

for a sequence of fine grained actions ${{{{\bf{Z}}}}}_{\hat{z}\hat{z}}^{y},\ldots,{{{{\bf{Z}}}}}_{\hat{z}\hat{z}}^{{{{\rm{a}}}}}$, and each ${{{{\bf{Z}}}}}_{\hat{z}\hat{z}}^{\alpha }$ is the fine-grained equivalent of ${{{{\bf{Z}}}}}_{\hat{\alpha }\hat{\alpha }}$ ⬜.

Proof of Obs. 1

Lem. 1 provides the language with which it is possible to show Obs. 1, that temporal coarse-graining is order-reflecting, i.e. at least as many processes can be reached by applying a superprocess and then coarse-graining, compared to coarse-graining and then applying a superprocess. We show that the latter can always be re-written in the form of Lem. 1, but that the converse is false in general.

The fact that temporal coarse-graining is order reflecting follows straightforwardly from Lem. 1. By this lemma, the ‘coarse-grain then apply control’ transformation $\left.\left.{{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]\left[\!\!\left[{{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}| {{{{\bf{Z}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]\left.\left.:= {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]{{{{\bf{Z}}}}}_{\hat{m}}$ can always be represented by some ‘apply control then coarse-grain’ transformation ${{{{\bf{Z}}}}}_{\hat{n}}^{{\prime} }\left.\left.| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]$ for an appropriate choice of ${{{{\bf{Z}}}}}_{\hat{n}}^{{\prime} }$.

To see why temporal coarse-graining is not in general also order preserving, simply consider when $\hat{n}\supset \hat{m}$ is a strict inclusion. This ${{{{\bf{Z}}}}}_{\hat{n}}^{{\prime} }$ will then be restricted in that no non-trivial actions may occur at times in $\hat{n}\setminus \hat{m}$. There are fewer times to exert influence on the system, naturally meaning that less can be done to transform it.

This observation shows that temporal resolution itself can be a resource, since its presence increases the range of processes one can transform to via free operations. This formalises the natural intuition about the relation of temporal resolution and control, and allows us to exploit this consequential connection.

Monotone interpretation of irreversibility

It is possible to re-frame irreversibility in terms of monotones. The following inequality follows directly from the original definition of irreversibility in Obs. 1.

Corollary 1

For any valid monotone $M:{\mathsf{T}}\to {{\mathbb{R}}}_{\ge 0}$ in a resource theory of temporal resolution S, and all process tensors ${{{{\bf{T}}}}}_{\hat{n}}\in {\mathsf{T}}$, with ${{\emptyset}}\subseteq \hat{m}\subseteq \hat{n}$

$$\begin{array}{rlr}&\mathop{\sup }\limits_{{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\in {{\mathsf{Z}}}_{\hat{n}\hat{n}}}M\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]\right)&\\ \ge &\mathop{\sup }\limits_{{{{{\bf{Z}}}}}_{\hat{m}\hat{m}}\in {{\mathsf{Z}}}_{\hat{m}\hat{m}}}M\left(\left[\!\!\left[\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}\setminus \hat{m}}\right]\!\!\right]| {{{{\bf{Z}}}}}_{\hat{m}\hat{m}}\right]\!\!\right]\right).\end{array}$$

(21)

The notation ${{\mathsf{Z}}}_{\hat{n}\hat{n}}$ denotes the set of free transformations from $\hat{n}$ interventions to $\hat{n}$ interventions. This holds true because monotones in resource theories satisfy A ↦ B via a free operations, then M(A) ≥ M(B) for all monotones, and Obs. 1 guarantees that the left hand side of Eq. (21) can reach at least as many processes as the right hand side. Given the same underlying dynamics, a finer grained process tensor description will always be at least as resourceful as the corresponding coarse-grained one.

Irreversibility leads to perceived non-monotonicity

What makes IQI suitable for describing noise reduction is that an appropriately chosen superprocess may cause the mutual information of the resultant channel to be higher than it would be without that intervention. In other words, the ability to reduce noise is inherently tied to the irreversibility of coarse-grainings.

Corollary 2

In the resource theory of temporal resolution IQI, given any process ${{{{\bf{T}}}}}_{\hat{n}}$, there exists a superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ such that

$${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}({{{{\bf{T}}}}}_{\hat{n}})\, > \,{I}_{{{\emptyset}}}({{{{\bf{T}}}}}_{\hat{n}})$$

(22)

iff Cor. 1 is realised as a strict inequality for $\hat{m}={{\emptyset}}$.

Proof

Consider Eq. (21) in the case of M = I and $\hat{m}={{\emptyset}}$. Then, Cor. 1 reduces to

$$\mathop{\sup }\limits_{{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\in {{\mathsf{Z}}}_{\hat{n}\hat{n}}}{I}_{{{\emptyset}}}\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)\ge {I}_{{{\emptyset}}}({{{{\bf{T}}}}}_{\hat{n}}).$$

(23)

Observe that the supremum on the right hand side disappears because free superprocesses in IQI with no intermediate interventions $\left[\!\left[{{{{\bf{I}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\right]$ are just mutually independent pre- and post-processing, and cannot increase mutual information (due to the data processing inequality), i.e.

$$\mathop{\sup }\limits_{{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\in {{\mathsf{Z}}}_{\hat{n}\hat{n}}}I\left(\left[\!\!\left[\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]| \left[\!\!\left[{{{{\bf{I}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]\right.\right.\right)={I}_{{{\emptyset}}}({{{{\bf{T}}}}}_{\hat{n}}).$$

(24)

Thus, if Cor. 1 holds as a strict inequality, then there will exist a superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ satisfying the strict inequality for Eq. (23). Conversely, if there exists any ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}({{{{\bf{T}}}}}_{\hat{n}})\, > \,{I}_{{{\emptyset}}}({{{{\bf{T}}}}}_{\hat{n}})$, Cor. 1 will be a strict inequality for the same reason that mutually independent pre- and post-processing cannot increase mutual information. Thus, noise reduction requires the irreversibility of temporal coarse-grainings ⬜.

Contractivity of relative entropy under coarse-grainings

As a pre-requisite for IQI to be considered a useful resource theory for describing information preservation, we require that mutual information is respected as a monotone. It is already known that free superprocesses ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ that do not change the number of times respect this quantity³⁶. Here, we show that mutual information is also contractive under temporal coarse-graining and thus a meaningful monotone of IQI. The proof of contractivity, which can be found in the Supplementary Methods, consists of showing that coarse-graining is a linear and positive operation that is trace preserving on the set of processes. As demonstrated in Ref. ⁶¹ (Thm. 1), these properties ensure contractivity of relative entropy (and thus mutual information). Specifically, trace preservation, and positivity are shown by writing the Choi state of a process, before and after coarse-graining, in terms of the composition of channels acting on maximally entangled states. Linearity is shown directly.

Monotonicity of I, M, N under free superprocesses of IQI

Clearly, mutual information $I({{{{\bf{T}}}}}_{\hat{n}})$ is a metric of how well a process ${{{{\bf{T}}}}}_{\hat{n}}$ retains information, and likewise for its constituents M and N. However, to show that our resource theory IQI actually treats the preservation of information as valuable, it should be true that those functions are all monotones under the free transformations. Here we show that I, M, and N are monotonic under free superprocesses of IQI. Importantly, our contractivity result proved in the Supplementary Methods guarantees that they are also monotonic under coarse-grainings, and hence the transformations of IQI more broadly, since all free transformations can be represented as a combination thereof. It is also the case that I is a faithful monotone in this theory. Note that monotonicity of these quantities does not conflict with our notion of ‘increasing’ these monotones throughout the text, since the reference is the case of no direct experimental intervention, not the pre-transformation process (see Fig. 2).

Proposition 1

Markovian information M and Non-Markovianity N, as defined in Eq. (6) and Eq. (7), respectively, are monotonic under the free superprocesses of IQI.

Proof

In resource theory IQI, all experimental interventions are temporally local, which means that they cannot increase correlations between temporally separated subsystems. To demonstrate this for the case of M, a free superprocess ${{{{\bf{Z}}}}}_{\hat{n}\hat{n}}$ is applied to ${{{{\bf{T}}}}}_{\hat{n}}$, and Markovian information takes the form

$$\begin{array}{ll}&M\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)\\ =&S\left({\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)}^{{{{\rm{Mkv}}}}}\parallel {\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)}^{{{{\rm{marg}}}}}\right)\\ =&S\left(\mathop{\bigotimes}\limits_{j=1}^{n+1}{{{{\rm{tr}}}}}_{\bar{j}}\left\{\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right\}\parallel\mathop{\bigotimes}\limits_{k=1}^{2(n+1)}{{{{\rm{tr}}}}}_{\bar{k}}\left\{\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right\}\right)\\ =&S\left(\left[\!\!\left[\mathop{\bigotimes}\limits_{j=1}^{n+1}{{{{\rm{tr}}}}}_{\bar{j}}\{{{{{\bf{T}}}}}_{\hat{n}}\}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\Bigg\Vert \left[\!\!\left[\mathop{\bigotimes}\limits_{k=1}^{2(n+1)}{{{{\rm{tr}}}}}_{\bar{k}}\{{{{{\bf{T}}}}}_{\hat{n}}\}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)\\ =&S\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\parallel \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)\\ \le &S\left({{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}\parallel {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\right)=M({{{{\bf{T}}}}}_{\hat{n}}).\end{array}$$

(25)

j indexes the evolutions of the process tensor, while h labels the input and output Hilbert spaces. The third line follows from the second because free superprocesses are temporally local in IQI, implying that the marginals (either full or Markovian as in Eq. (6)) of the transformed process equals the the transformation of the marginals, i.e. ${\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)}^{{{{\rm{Mkv}}}}}=\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]$, and ${\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)}^{{{{\rm{marg}}}}}=\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]$. The final line uses the contractivity of relatve entropy under free superprocesses³⁶. The same type of argument can be applied to show that I and N are monotones, so we will not repeat it ⬜.

It should be noted that this feature of the independent quantum instruments theory does not hold for all RTTRs. Specifically, when the individual actions within the superprocess are connected by memory, the second line in Eq. (25) will not equal the third, and these quantities may no longer be monotones. For example, some (but not all) non-Markovian processes may be considered free in a theory that allows for convex mixtures of the allowed superprocesses in IQI, meaning that N is no longer a monotone.

Most importantly, since we understand IQI as a resource theory for noise reduction, the fact that N is a monotone in this theory means that non-Markovianity is a resource for noise mitigation in general.

Invariance of I, M, N under Superprocesses of IU

We present a brief proof that total mutual information, Markovian information, and non-Markovianity are not only monotonic, but also invariant under DD sequences, and the free superprocesses of IU more broadly, i.e. sequences of unitaries. We emphasise that this invariance is with respect to superprocesses is in the absence of coarse-graining, i.e. only holds at a single level of temporal resolution. Again, this does not contradict the possibility of noise mitigation/DD, since the reference is not the process before transformation, but the result which would be obtained if the experimenter did not intervene.

Proposition 2

I, M, and N are invariant under the free superprocesses of IU.

Proof

We show this invariance directly for I, using the same argument as in our proof of Prop. 1:

$$\begin{array}{lll}I\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)&=&\,S\left({{{{\bf{T}}}}}_{\hat{n}}\parallel {\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)}^{{{{\rm{marg}}}}}\right)\,\\ &=& S\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\parallel \mathop{\bigotimes}\limits_{h=1}^{2(n+1)}{{{{\rm{tr}}}}}_{\bar{h}}\{\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\}\right)\\ &=& S\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\parallel \left[\!\!\left[\mathop{\bigotimes }\limits_{h=1}^{2(n+1)}{{{{\rm{tr}}}}}_{\bar{h}}\{{{{{\bf{T}}}}}_{\hat{n}}\}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)\\ &=& S\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\parallel \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}\right]\!\!\right]\right)\\ &=& I({{{{\bf{T}}}}}_{\hat{n}}).\end{array}$$

(26)

As with Prop. 1, the second and third line are equal because the free superprocesses of IU ⊂ IQI are temporally local. The invariance of M and N follow from the same argument, so we will not repeat it here ⬜.

The fact that even the cleanest (i.e. unitary) interventions still cannot increase the value of monotones highlights the pivotal role of temporal coarse-graining in noise reduction.

Derivation of Eq. 8

In this subsection we demonstrate that important property that the partition of $I({{{{\bf{T}}}}}_{\hat{n}})$ into $N({{{{\bf{T}}}}}_{\hat{n}})+M({{{{\bf{T}}}}}_{\hat{n}})$ has no overlap, i.e. that the trade-off between Markovian and non-Markovian correlations is a ‘zero-sum game’. We express the difference between $I({{{{\bf{T}}}}}_{\hat{n}})$ and $M({{{{\bf{T}}}}}_{\hat{n}})$ in terms $N({{{{\bf{T}}}}}_{\hat{n}})$:

$$\begin{array}{lll}I({{{{\bf{T}}}}}_{\hat{n}})-I({{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}})&=& S\left({{{{\bf{T}}}}}_{\hat{n}}\parallel {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\right)-S\left({{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}\parallel {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\right)\\ &=& \left(S\left({{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\right)-S\left({{{{\bf{T}}}}}_{\hat{n}}\right)\right)\\ &&-\, \left(S\left({{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}\right)-S\left({{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}\right)\right)\\ &=& S\left({{{{\bf{T}}}}}_{\hat{n}}\parallel {{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}\right)=N({{{{\bf{T}}}}}_{\hat{n}}).\end{array}$$

(27)

The above holds because ${{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}$ is a product of marginals of ${{{{\bf{T}}}}}_{\hat{n}}$, while ${{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{marg}}}}}$ is a product of marginals of ${{{{\bf{T}}}}}_{\hat{n}}^{{{{\rm{Mkv}}}}}$. Hence, the mutual information monotone can be partitioned into two contributions

$$I({{{{\bf{T}}}}}_{\hat{n}})=M({{{{\bf{T}}}}}_{\hat{n}})+N({{{{\bf{T}}}}}_{\hat{n}}),$$

(28)

allowing us to study the role of non-Markovianity (captured by $N({{{{\bf{T}}}}}_{\hat{n}})$) in information preservation.

Dynamical decoupling technique and numerical model

Noise model

The model used to generate the data underlying Fig. 4 consists of a a single qubit system s, and a single qubit environment e with a (Haar) randomly sampled initial pure state ${\rho }_{0}^{{{{\rm{e}}}}}$, undergoing evolution for duration t under a randomly sampled s-e Hamiltonian H^se whose operator norm is normalised to unity. Specifically, these Hamiltonians are sampled by producing matrices K whose entries are uniformily distributed in [0, 1], taking H^se as the combination K + K^†, and subsequently normalising it by its operator norm. The choice of a simple unitary noise model ensures that DD is possible at least in principle. In a noise model such as this, non-Markovianity will gradually accumulate as the duration between pulses becomes longer, instead of information being irreversibly lost to structureless noise.

We produce 20 samples of pairs $\{{\rho }_{0}^{{{{\rm{e}}}}},{H}^{{{{\rm{se}}}}}\}$, generating an ensemble of 20 sets of underlying dynamics. Due to the fact that a two-qubit Hamiltonian does not equilibrate for long times, and instead oscillates, combined with our use of a log scale to probe many timescales, this oscillatory behaviour will tend to obscure any real trends at long times. Hence, there is a need to average in the time domain to smooth over these oscillations at long timescales. Specifically, for each time data point, a window of 10 data points was averaged over to generate the value for that time.

For a given set of underlying dynamics, we study three levels of temporal resolution: ${{{{\bf{T}}}}}_{\hat{15}}$, $\hat{15}=\{t/16,\ldots,15t/16\}$, ${{{{\bf{T}}}}}_{\hat{3}}$, $\hat{3}=\{t/4,2t/4,3t/4\}$, and ${{{{\bf{T}}}}}_{{{\emptyset}}}$, corresponding to a fine-grained process, an intermediate process, and a channel. DD can be applied at the fine-grained level, and/or at the coarse-grained level, by acting at both timescales corresponding to CDD. Using these three levels of temporal resolution, we can compute changes in monotones, e.g. ${{\Delta }}I={I}_{\hat{3}| {{{{\bf{Z}}}}}_{\hat{15}\hat{15}}}({{{{\bf{T}}}}}_{\hat{15}})-{I}_{\hat{3}}({{{{\bf{T}}}}}_{\hat{15}})$, as well as the increase in channel-level mutual information ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{15}\hat{15}}}({{{{\bf{T}}}}}_{\hat{15}})-{I}_{{{\emptyset}}}({{{{\bf{T}}}}}_{\hat{15}})$.

Applying MODD to noise model

We summarise the process of applying MODD to the noise model above. In the case with n = 15 that we consider, we have the number of segments at the fine timescale K⁰ = 4, and the first segment being ${\hat{m}}_{1}=\{t/16,2t/16,3t/16\}$ (see Fig. 4 (a)). Using this optimised sequence, a maximally mixed state is placed into the input of the dynamics at time t = 0 and the second segment on times ${\hat{m}}_{2}=\{5t/16,6t/16,7t/16\}$ is characterised (experimentally, this would be done by tomography, for our numerical simulation, we can directly compute it) and the corresponding sequence of operations is optimised via ODD (see the SDP methods described below in Sec. SDP Methods). This procedure is continued until all of $\hat{n}=\hat{15}$ has optimised operations. We then coarse-grain ${{{{\bf{T}}}}}_{\hat{n}}$ (by contracting it with the found sequence of operations ${{{{\mathcal{A}}}}}_{i}$) to ${{{{\bf{T}}}}}_{{\hat{n}}^{{\prime} }}$ where ${\hat{n}}^{{\prime} }=\{t/4,t/2,3t/4\}$. This does not need to be further split into segments, so we set K¹ = 1. Finally, we perform a last SDP optimisation on ${{{{\bf{T}}}}}_{{\hat{n}}^{{\prime} }}$. This procedure then yields a sequence of n (in our case, n = 15) operations that achieve a good level of decoupling. In our numerical study we use two timescales (C = 2): one fine timescale, and one coarse one, but in general one can continue coarse-graining and optimising at longer timescales. This is directly analogous to the levels of concatenation in CDD.

Importantly, this multitimescale ODD approach overcomes the exponentially bad scaling that ODD is plagued by on its own, since it only requires the characterisation of n/m + 1 processes on m times (for one layer of coarse-graining). For example, for the case n = 15 and m = 3 outlined above, MODD requires the characterisation of five three-slot combs, each necessitating the experimental collection of d¹⁶ probabilities, as compared to d⁶⁴ for the complete 15 slot process. Despite the linear scaling (with respect to the characterisation of the m-slot process), the drawback of this method is that it only finds local maxima based on a series of individual optimisations, as opposed to a global optimisation over the uncomputable full process. MODD mitigates this shortcoming by following up the original optimisation with a ‘more global’ optimisation at a coarser timescale, thus exploiting both short- and long-term memory effects.

SDP methods

As mentioned in Sec. Numerical Optimisation, direct optimisation of a set of control operations for a given process tensor ${{{{\bf{T}}}}}_{\hat{n}}$ requires the maximisation of ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}$, i.e. one aims to solve

$$\begin{array}{rl}{{{\bf{given}}}} & {{{{\bf{T}}}}}_{\hat{n}}\\ {{{\bf{maximize}}}} &{I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}({{{{\bf{T}}}}}_{\hat{n}}):= I\left(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]\right)\\ {{{\bf{subject}}}}\,{{{\bf{to}}}} & \left.\left.{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]=\left.\left.| {{{{\mathcal{A}}}}}_{1}\otimes \cdots \otimes {{{{\mathcal{A}}}}}_{n}\right]\!\!\right]\,,\\ &{{{{\mathcal{A}}}}}_{1},\ldots {{{{\mathcal{A}}}}}_{n}{{{\rm{are}}}}\,{{{\rm{CPTP}}}}.\end{array}$$

(29)

This problem is neither linear nor convex with respect to the variables ${{{{\mathcal{A}}}}}_{i}$, and the mutual information is not amenable to simple optimisation techniques. Here, we overcome these issues by iteratively optimising over each of the involved variables individually and replacing the mutual information by a proxy, specifically the largest eigenvalue of ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}({{{{\bf{T}}}}}_{\hat{n}})$. For a given $\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]$, computation of the largest eigenvalue is an SDP:

$$\begin{array}{rl}{{{\bf{given}}}} & \left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]\\ {{{\bf{maximize}}}} & \lambda ={{{\rm{tr}}}}(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]E)\\ {{{\bf{subject}}}}\,{{{\bf{to}}}} & 0\le E\le {\mathbb{1}}\end{array}$$

(30)

With this, in each iteration step, one can efficiently optimise over one of the variables ${{{{\mathcal{A}}}}}_{1},\ldots,{{{{\mathcal{A}}}}}_{n},E$ while keeping the others fixed. For example, in order to optimise ${{{{\mathcal{A}}}}}_{1}$, one would solve the SDP

$$\begin{array}{rl}{{{\bf{given}}}}&{{{{\mathcal{A}}}}}_{2},\ldots {{{{\mathcal{A}}}}}_{n},E\\ {{{\bf{maximize}}}}&\lambda ={{{\rm{tr}}}}(\left[\!\!\left[{{{{\bf{T}}}}}_{\hat{n}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]E)\\ {{{\bf{subject}}}}\,{{{\bf{to}}}}&\left.\left.{{{{\bf{Z}}}}}_{\hat{n}\hat{n}}| {{{{\bf{I}}}}}_{\hat{n}}\right]\!\!\right]=\left.\left.| {{{{\mathcal{A}}}}}_{1}\otimes \cdots \otimes {{{{\mathcal{A}}}}}_{n}\right]\!\!\right]\,,\\ &{{{{\mathcal{A}}}}}_{1}{{{\rm{is}}}}\,{{{\rm{CPTP.}}}}\end{array}$$

(31)

Consecutively optimising all variables until the largest eigenvalue λ does not change anymore then yields a heuristic guess for a good sequence that maximises ${I}_{{{\emptyset}}| {{{{\bf{Z}}}}}_{\hat{n}\hat{n}}}({{{{\bf{T}}}}}_{\hat{n}})$ which we compute as a final step for the sequence ${{{{\mathcal{A}}}}}_{1},\ldots,{{{{\mathcal{A}}}}}_{n}$ obtained from the above procedure. Evidently, the solutions found in this way are not necessarily globally ideal; firstly, such an iterative approach is only guaranteed to converge to a local, but not necessarily a global extremum. Secondly, we only maximise a proxy for the mutual information of the resulting channel, namely the largest eigenvalue of the resulting channel. Consequently, there might be better solutions than the ones we provide, and more bespoke numerical techniques to find ideal control sequences. In all the cases we consider, though, this approach already yields significant advantages over traditional DD sequences.