Abstract
In the Ultimatum Game, two players are offered a chance to win a pie. The proposer suggests how to split the pie. The responder can either accept or reject the deal. If an agreement is not reached, neither player gets anything. Both game theory and evolutionary game theory predict the rational solution that the proposer offers the smallest possible share and the responder accepts it. Fairness thus requires additional mechanisms for natural selection to favor it. Studies to date assumed that individuals have competed for the fixed size of pies, in sharp contrast with real situations, where randomness is ubiquitous. Here we study the impact of random allocation of pies on the evolution of fairness in the Ultimatum Game. Interestingly, we find that the evolution of fairness can be promoted by the randomness associated with the size of pies, without the support of any additional evolutionary mechanisms.
Similar content being viewed by others
Introduction
The Ultimatum Game has become a popular paradigm for investigating and elucidating the evolution of fairness1. In this simple game, two players, one acting as a proposer and the other as a responder, have to share a pie. The proposer suggests a split of the pie and the responder can either accept it or not. If the responder accepts the offer, the deal is done. If the responder rejects the offer, neither player obtains anything. Apparently, a rational responder should accept any nonzero offer, or else he will end up with getting nothing and thus a selfish proposer should always claim the large majority of the pie, which is known as the subgame perfect equilibrium in game theory2. This is also the observed outcome for the evolutionary Ultimatum Game in a well-mixed population3. However, large amount of empirical experiments show that the majority of proposers offer 40% to 50% of the total sum and about half of responders reject offers below 30%1,4,5,6,7,8,9, which is obviously at odds with above analytical reasoning. Then how can we understand the emergence and persistence of fairness in a population of self-interest individuals?
Recently, considerable efforts have been made to explore the origins of this altruistic behaviour. Some studies have demonstrated that many people are not only concerned with their own benefits but also influenced by the payoffs of others, which is usually considered in the definitions of utility functions8,10,11,12,13. While others have shown that the preference of people towards fairness may be due to the repeated interactions in the Ultimatum Game6,8,13,14. In the context of evolutionary game theory15, theoretical studies indicate that small group size16, reputation17, empathy18, population structure19,20,21,22,23,24,25,26,27,28,29 and heterogeneity30,31 play a vital role in the evolution of fairness in the Ultimatum Game.
To our knowledge, an important issue, which has so far remained unexplored, is how the random allocation of pies affects the evolution of fairness in the Ultimatum Game. In hunter-gatherer societies32, the Ultimatum Game can describe such a situation, where two individuals have to divide in advance the reward of a task which can be obtained only by jointly effort, such as cooperative hunting, forming an alliance against another group member, or food sharing. Obviously, there is no reason that the sizes of rewards must be uniform. Let us take cooperative hunting as an example. It apparently can not be guaranteed that the prey is always the same for each hunting activity. Actually, it seems more plausible to assume that the sizes of pies are subject to some kind of distribution, which motivates us to model and study the random allocation scheme of pies in the Ultimatum Game under the framework of evolutionary game theory (see Model definition in Methods section). Interestingly, we find that whenever individuals compete for stochastic sizes of pies (introduced by random allocation scheme), evolution can lead to fairer split, without the support of any additional evolutionary mechanisms. Our results thus demonstrate how the randomness can be crucial for the emergence and maintenance of fairness.
Results
In this report, we mainly focus on how the amplitude of fluctuation of the pies, Λ, influences the evolution of fairness in the Ultimatum Game. The strategy of a player is given by a vector S = [p, q], where p represents the offer level, i.e., the fraction of the pie offered by the player when acting as a proposer and q indicates the acceptance threshold, i.e., the minimum fraction that the player accepts when acting as a responder.
We start by studying how local random allocation scheme of pies affects the evolution of fairness in the spatial Ultimatum Game. It should be noticed that Λ = 0 recovers the original spatial Ultimatum Game19, wherein uniform allocation scheme of pies is adopted. With the increment of Λ, the allocated pies become increasingly stochastic. Figure 1 shows the results for the evolution of fairness across the whole applicable span of Λ. Comparison between the results on uniform allocation scheme (i.e., Λ = 0) with those on local random allocation scheme (i.e., 0 < Λ ≤ 1) reveals the impact of randomness on the evolution of fairness. For uniform allocation scheme, the population evolves towards a state deviating from the game-theoretic prediction and equilibrates at  and
and  on spatial networks, which is similar to the positive effect of network structure on facilitating cooperation33,34,35,36,37. As Λ increases, both
on spatial networks, which is similar to the positive effect of network structure on facilitating cooperation33,34,35,36,37. As Λ increases, both  and
and  monotonically increase and reach their own maximums (i.e.,
monotonically increase and reach their own maximums (i.e.,  and
and  ) at Λ = 1.
) at Λ = 1.
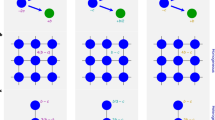
The time evolution of typical spatial strategy distributions for Λ = 0 and Λ = 1 is depicted in Figs. 2(a) and 2(b), respectively. Generally, the evolutionary process for the case of Λ = 0 can be characterized by two distinct dynamical phases: local aggregation (from t = 1 to t = 10) followed by global expansion (from t = 10 to t = 10000). Initially, self-incompatible strategies (i.e., strategies satisfying p < q) are extinct after the first few time steps [see t = 10 for Λ = 0 in Fig. 2(a)]. Such strategies obtain nothing when interacting with themselves. Consequently, they will disappear in a spatial world. On the other hand, self-compatible strategies (i.e., strategies satisfying p ≥ q), which can be roughly classified into two categories: generous strategies (i.e., strategies that satisfy the condition that p is large, while q is small) and quasiempathic strategies (i.e., strategies that satisfy the condition that p and q are similar with each other.), gradually form spatial clusters in a self-organized manner [see t = 10 for Λ = 0 in Fig. 2(a)]. Therefore, we can make the macroscopic observation that the average offer level of the population increases, while the average acceptance threshold decreases in this stage [see t = 1 and t = 10 for Λ = 0 in Fig. 2(a)]. Subsequently, the system enters into the global expansion phase. The more fair quasiempathic strategies can expand into the territories of the less fair quasiempathic and the generous ones in the form of spatial clusters. We emphasize that theories related to spatial selection of cooperators in the prisoner's dilemma game38 or the public goods game39 do not help explain fairness in the Ultimatum Game at this stage, as a cluster of individuals with more fair quasiempathic strategies receives the same average payoff as a cluster of individuals with less fair quasiempathic strategies or generous ones. On the contrary, it is the performance of one strategy against other strategies that determines its own evolutionary fate. With these facts in mind, we can explain the above phenomenon by considering the following situation: a player with more fair quasiempathic strategy S2 = [p2, q2] competes with another player with less fair quasiempathic strategy S1 = [p1, q1]. Then the following two cases should be considered: (a)  or
or  and (b)
and (b)  . The payoff difference between the player with S2 and the one with S1 is 2(p1 − p2) if condition (a) holds and 1 − 2p2 if condition (b) holds. Obviously, it is advantageous for players to enhance their acceptance thresholds. Though it gives a good estimation of the local competition between players on spatial networks especially if the connectivity is low, this simple analysis ignores the fact that the performance of a player depends not merely on one single interaction, but on the interactions with players in the whole neighborhood. From this perspective, players are tempted to lower their acceptance thresholds. Put differently, there is a tradeoff between rejecting unfair offers (achieving by increasing q) and making more successful splits (achieving by decreasing q) for players in structured populations. As a result, we can inspect a sharp increase of the average acceptance threshold of the population from a low level at t = 10 to a moderate level at t = 100, while a relatively moderate increase of the average offer level of the population in this stage [see t = 10 and t = 100 for Λ = 0 in Fig. 2(a)]. Still, there are a few small residual clusters of generous strategies embedded in a spatial world of fair quasiempathic strategies at t = 100. The offer level of each player is roughly equal [σp ≈ 0.0328 at t = 100, see Fig. 2(a)]. On the other hand, the strategies surviving in the structured population are self-compatible [see Fig. 2(a)]. Both factors lead to the result that the payoff of each player is approximately equal in the population. The strategy evolution is largely controlled by slowly coarsening dynamics, which is similar to the behaviour of the voter model40. Since the fraction of fair quasiempathic strategies is much higher compared to the fraction of generous ones, the fair quasiempathic strategies will take over the whole population eventually [see t = 100 and t = 10000 for Λ = 0 in Fig. 2(a)]. Regarding the case of Λ = 1, we inspect a very similar evolutionary process as Λ = 0 [see Fig. 2(b)].
. The payoff difference between the player with S2 and the one with S1 is 2(p1 − p2) if condition (a) holds and 1 − 2p2 if condition (b) holds. Obviously, it is advantageous for players to enhance their acceptance thresholds. Though it gives a good estimation of the local competition between players on spatial networks especially if the connectivity is low, this simple analysis ignores the fact that the performance of a player depends not merely on one single interaction, but on the interactions with players in the whole neighborhood. From this perspective, players are tempted to lower their acceptance thresholds. Put differently, there is a tradeoff between rejecting unfair offers (achieving by increasing q) and making more successful splits (achieving by decreasing q) for players in structured populations. As a result, we can inspect a sharp increase of the average acceptance threshold of the population from a low level at t = 10 to a moderate level at t = 100, while a relatively moderate increase of the average offer level of the population in this stage [see t = 10 and t = 100 for Λ = 0 in Fig. 2(a)]. Still, there are a few small residual clusters of generous strategies embedded in a spatial world of fair quasiempathic strategies at t = 100. The offer level of each player is roughly equal [σp ≈ 0.0328 at t = 100, see Fig. 2(a)]. On the other hand, the strategies surviving in the structured population are self-compatible [see Fig. 2(a)]. Both factors lead to the result that the payoff of each player is approximately equal in the population. The strategy evolution is largely controlled by slowly coarsening dynamics, which is similar to the behaviour of the voter model40. Since the fraction of fair quasiempathic strategies is much higher compared to the fraction of generous ones, the fair quasiempathic strategies will take over the whole population eventually [see t = 100 and t = 10000 for Λ = 0 in Fig. 2(a)]. Regarding the case of Λ = 1, we inspect a very similar evolutionary process as Λ = 0 [see Fig. 2(b)].
Evolutionary process of characteristic spatial strategy distributions emerging for (a) Λ = 0 and (b) Λ = 1 starting from identical random initial conditions.
(a) t = 1:  and σp ≈ 0.147,
and σp ≈ 0.147,  and σq ≈ 0.148 and
and σq ≈ 0.148 and  and σp–q ≈ 0.208. t = 10:
and σp–q ≈ 0.208. t = 10:  and σp ≈ 0.0828,
and σp ≈ 0.0828,  and σq ≈ 0.109 and
and σq ≈ 0.109 and  and σp–q ≈ 0.103. t = 100:
and σp–q ≈ 0.103. t = 100:  and σp ≈ 0.0328,
and σp ≈ 0.0328,  and σq ≈ 0.0629 and
and σq ≈ 0.0629 and  and σp–q ≈ 0.0492. t = 10000:
and σp–q ≈ 0.0492. t = 10000:  and σp ≈ 0.0176,
and σp ≈ 0.0176,  and σq ≈ 0.0220 and
and σq ≈ 0.0220 and  and σp–q ≈ 0.0148. (b) t = 1:
and σp–q ≈ 0.0148. (b) t = 1:  and σp ≈ 0.147,
and σp ≈ 0.147,  and σq ≈ 0.148 and
and σq ≈ 0.148 and  and σp–q ≈ 0.208. t = 10:
and σp–q ≈ 0.208. t = 10:  and σp ≈ 0.0875,
and σp ≈ 0.0875,  and σq ≈ 0.110 and
and σq ≈ 0.110 and  and σp–q ≈ 0.110. t = 100:
and σp–q ≈ 0.110. t = 100:  and σp ≈ 0.0389,
and σp ≈ 0.0389,  and σq ≈ 0.0637 and
and σq ≈ 0.0637 and  and σp–q ≈ 0.0439. t = 10000:
and σp–q ≈ 0.0439. t = 10000:  and σp ≈ 0.0165,
and σp ≈ 0.0165,  and σq ≈ 0.0230 and
and σq ≈ 0.0230 and  and σp–q ~~ 0.0187. Other parameters: K = 0.1 and ε = 0.005.
and σp–q ~~ 0.0187. Other parameters: K = 0.1 and ε = 0.005.
For the purpose of shedding light on the constructive impact of local random allocation scheme of pies on the evolutionary success of fairness in our agent based simulations, we turn to consider a mini spatial Ultimatum Game17,19,41, in which only two strategies, i.e., S1 = [p1, q1] and S2 = [p2, q2] satisfying  , are present. It was previously reported that the fate of a random arrangement of two strategies on the two-dimensional grid relies on whether a 3 × 3 cluster of one strategy can spread or not19,41. We thus investigate how the invasion ability of a 3 × 3 S2 mutant cluster varies with Λ in a spatial world of players with strategy S1. In Supplementary Note, we find that the parameter region, under which the 3 × 3 S2 mutant cluster is expected to expand [i.e.,
, are present. It was previously reported that the fate of a random arrangement of two strategies on the two-dimensional grid relies on whether a 3 × 3 cluster of one strategy can spread or not19,41. We thus investigate how the invasion ability of a 3 × 3 S2 mutant cluster varies with Λ in a spatial world of players with strategy S1. In Supplementary Note, we find that the parameter region, under which the 3 × 3 S2 mutant cluster is expected to expand [i.e.,  ], is enlarged when Λ increases (see Supplementary Fig. S13). More intriguingly, there exists a intermediate value of Λ that leads to the most favorable condition for the evolution of fairness in the mini spatial Ultimatum Game. Such observation reminds us of the coherence resonance phenomenon in dynamical systems, where noise can anticipate the behaviour of the system past a bifurcation point in a resonant manner42,43,44,45,46. Indeed, results presented in Supplementary Fig. S13 clearly show that there exists an optimal Λ for which the parameter region of
], is enlarged when Λ increases (see Supplementary Fig. S13). More intriguingly, there exists a intermediate value of Λ that leads to the most favorable condition for the evolution of fairness in the mini spatial Ultimatum Game. Such observation reminds us of the coherence resonance phenomenon in dynamical systems, where noise can anticipate the behaviour of the system past a bifurcation point in a resonant manner42,43,44,45,46. Indeed, results presented in Supplementary Fig. S13 clearly show that there exists an optimal Λ for which the parameter region of  is maximal. As a matter of fact,
is maximal. As a matter of fact,  can be assumed to represent the constructive effects of noise on the system and has similar meaning as the signal-to-noise ratio in dynamical systems42. Then we can regard the phase transition as a bifurcation point of a dynamical system. This conjecture can be strengthened by considering that the parameter p2 in the noisy regime truly acts as a bifurcation parameter, since increasing its value pushes the system further away from the transition line, which makes it increasingly difficult for noise to anticipate the behaviour of the system beyond the bifurcation (see Supplementary Fig. S13). Extensive computer simulations also show the existence of intermediate optimum Λ in the full spatial Ultimatum Game (i.e., with its continuum of strategies) by expanding Λ beyond the reasonable range [0, 1] and thus verify our explanation (see Supplementary Fig. S1).
can be assumed to represent the constructive effects of noise on the system and has similar meaning as the signal-to-noise ratio in dynamical systems42. Then we can regard the phase transition as a bifurcation point of a dynamical system. This conjecture can be strengthened by considering that the parameter p2 in the noisy regime truly acts as a bifurcation parameter, since increasing its value pushes the system further away from the transition line, which makes it increasingly difficult for noise to anticipate the behaviour of the system beyond the bifurcation (see Supplementary Fig. S13). Extensive computer simulations also show the existence of intermediate optimum Λ in the full spatial Ultimatum Game (i.e., with its continuum of strategies) by expanding Λ beyond the reasonable range [0, 1] and thus verify our explanation (see Supplementary Fig. S1).
Figure 3 shows how fairness evolves if the randomness of pies is extended from local to global in the spatial Ultimatum Game. The results obtained here are qualitatively identical as the ones for the case of local random allocation scheme. Namely, as Λ increases, both the average offer level  and the average acceptance threshold
and the average acceptance threshold  of the population increase. Thus together with the results obtained from Fig. 1, one can conclude that the stochasticity in the sizes of pies facilitates the evolution of fairness in the spatial Ultimatum Game.
of the population increase. Thus together with the results obtained from Fig. 1, one can conclude that the stochasticity in the sizes of pies facilitates the evolution of fairness in the spatial Ultimatum Game.
To check the universality of the drawn conclusions, we have tested various aspects of the model. Considering a well-mixed population, a small-world network, or a scale-free network does not affect our qualitative results (see Supplementary Figs. S2, S3 and S4). Without the aid of “spatial reciprocity”19, the well-mixed population evolves into a considerably unfair state (see Supplementary Fig. S2). The degree of fairness increases compared with that observed on square lattices, when individuals interact on small-world networks. Namely, the small-world effect can further enhance the level of fairness (compare Figs. 1 and 3 with Supplementary Fig. S3). In contrast, the heterogeneity of the degree distribution disfavors fairness, as the level of fairness achieved in the scale-free networks is more modest in comparison with that observed on square lattices (compare Figs. 1 and 3 with Supplementary Fig. S4). This is in sharp contrast with other theoretical investigations that inhomogeneity of the networks can result in a remarkable boost in cooperation37,47. Altering the update rule (employing asynchronous updating rule) results in the same qualitative outcomes (see Supplementary Fig. S5). Applying overlapping generations (asynchronous updating) instead of non-overlapping generations (synchronous updating) can further elevate the degree of fairness (compare Figs. 1 and 3 with Supplementary Fig. S5). Moreover, the variation of noise or learning error does not affect our qualitative outcomes (see Supplementary Figs. S6 and S7). Moderately adjusting the noise as well as learning error does not alter the conclusion that random allocation of pies promotes the evolution of fairness. As a further test of robustness, we investigate another pattern of Ultimatum Game, in which the game is played only once between two parties and roles (proposer or responder) are randomly assigned to them. Again, we find qualitative equivalent behaviour (see Supplementary Fig. S8). Moreover, we also test another widely applied initial strategy distribution setup, in which the two components p and q of each individual's strategy vector [p, q] are initially picked up in the interval [0, 1] randomly and independently. We show that such change does not affect the generality of the reported results (see Supplementary Fig. S9). In addition, when replacing the uniform distribution of pies with exponential or power-law distribution, we find qualitatively the same results (see Supplementary Fig. S10). All the above results have indicated that the main conclusions are robust against a wide variety of perturbations of the model.
Discussion
In sum, we have studied how random allocation of pies affects the evolution of fairness in the spatial Ultimatum Game. It was found that the evolution of fairness can be promoted if randomness is involved in the allocation of pies. In order to elaborate the underlying reason for the facilitation of fairness, we have analyzed a mini spatial Ultimatum Game and found that the introduced randomness can favor fairness in a resonant manner, which is similar to coherence resonance in other dynamical systems36,42. This explanation is further supported by the observation of the resonant phenomenon made on the full spatial Ultimatum Game. Moreover, we have demonstrated that the main findings are robust against numerous variations of the model and thus designating the randomness of pies as a universal mechanism to promote the evolution of fairness.
Lastly, we would like to relate the present work to some other game-theoretical ones. By using stochastic evolutionary game theory, Rand et al.48 studied the effect of randomness on the evolution of fairness in the Ultimatum Game. Interestingly, they found that natural selection favors fairness, when selection is sufficiently weak or mutation is sufficiently high. However, such assumptions are not necessary in our study. Instead, we find that the randomness arising from the allocation of pies can promote the evolution of fairness in the Ultimatum Game even if selection is strong and mutation is low (see Supplementary Fig. S2). Note that it is the errors in social learning process and the finiteness of the populations that lead to the randomness in their study. Although the randomness origins from different aspects for these two works, both of them lead to the conclusion that fairness has a better chance to triumph in a random world.
In fact, the effect of the size of pies on the origin of fair behavior has also attracted lots of interests from experimental economists. In one setup of experimental designs49,50,51, the empirical studies assumed that the size of the pies to be allocated would decay over rounds until an agreement is reached. While in our model, the size is randomly changed during the evolutionary process and we focus on the one-round Ultimatum Game. In another pattern52,53, researchers investigate the Ultimatum Game with incomplete information, that is, both parties have limited information regarding the game (e.g., only proposer knows the size of pie, while the responder is merely informed about the probability distribution of possible pie sizes when responding to the proposal52.). In our study, however, players have no information about their co-players and they have completely no idea on the size of pies. Our analysis shows that randomness of pies facilitates the evolution of fairness in the Ultimatum Game even in such information-deficiency situation.
Methods
Model definition
The strategy of each player can be characterized by a vector S = [p, q]. The value of p denotes the fraction of the pie offered by the player when acting as a proposer, while the value of q indicates the acceptance threshold, i.e., the minimum fraction that the player accepts when acting as a responder. Each time step, every individual plays the Ultimatum Game with each of its neighbors, once in the role of proposer and once in the role of responder. Let P (Si, Sj) be the payoff that player i with strategy Si = [pi, qi] gets from player j with strategy Sj = [pj, qj]. Thus P(Si, Sj) is given by

where Ri (Rj) is the pie allocated to the Ultimatum Game, in which player i (j) acts as a proposer and j (i) as a responder. As far as we know, previous studies regarding the Ultimatum Game simply assume the uniform allocation scheme of pies, that is, the size of pies is constant (i.e., Ri = Rj = 1). In this report, we would like to relax this assumption and introduce randomness by considering random allocation scheme of pies.
Random allocation scheme
For random allocation scheme, pies are randomly allocated to the Ultimatum Games. As the first step to model the random allocation scheme and for the convenience of analysis, the pies Ri and Rj, which are split between player i and j, are simply assumed to be Ri = 1 + ξ and Rj = 1 − ξ, where ξ is a random variable and subject to uniform distribution ranging from −Λ to Λ [see Fig. 4(a)]. As the total size of pie Ri + Rj = 2 to be split between i and j is constant, the randomness of the allocation of pies is merely local in this case. Therefore, we term this mode of random allocation scheme as local random allocation scheme. Later, we will also investigate the so called global random allocation scheme, wherein Ri = 1 + ξi and Rj = 1 + ξj [see Fig. 4(b)]. Here ξi and ξj are independent random variables and subject to uniform distribution ranging from −Λ to Λ. The parameter Λ determines the amplitude of undulation of the pies. For reasonability of the model, we set 0 ≤ Λ ≤ 1 for both local and global random allocation schemes, making sure that Ri ≥ 0 and Rj ≥ 0. It is important to note that all the expectations of the above random variables equal to zero and thus there is no net contribution of both kinds of random allocation schemes to the total expected payoff of the population statistically.
Schematic diagram of (a) local and (b) global random allocation scheme.
In the diagram, the player at the end of the arrow plays as a proposer, while the one at the front of the arrow acts as a responder for each Ultimatum Game. The size of pie allocated to each Ultimatum Game is denoted at the middle of the arrow. Ri (Rj) is the pie to be split in one of the two Ultimatum Games played between player i and j, in which i (j) acts as the proposer and j (i) as the responder at time t. For both local and global random allocation scheme, the pies are randomly allocated to the Ultimatum Games. The difference lies in that the total size of pie Ri + Rj = 2 to be split between i and j is constant for local random allocation scheme.
Subsequently to the games, players consider updating their strategies. Every player accumulates the payoff and then would experience the strategy updating synchronously. Particularly, player i adopts the strategy Sj of a randomly selected neighbor j with the probability

where Pi and Pj are the payoffs of i and j, respectively. The parameter K quantifies the amplitude of noise36. As the strategies in the Ultimatum Game are continuous, it is almost impossible to imitate the strategy of the role model precisely. Thus we add a small perturbation to the process of strategy updating. Namely, after learning from j, the strategy of i becomes Si = [pi + ε1, qi + ε2] with ε1 and ε2 being randomly picked up from the interval [−ε, ε]. Both the noise K and the learning error ε are used to create a “trembling hand” effect2. After these updating events have been performed for all of the individuals in the population, a new time step begins.
Model parameters settings
The simulation results were obtained by applying a square lattice with the von Neumann neighborhood (i.e., the number of neighbors for each site is 4), which is of size N = 100 × 100 and with periodic boundary condition. Based on rational self-interest, the two components p and q of each individual's strategy vector [p, q] are initially picked up in the interval [0, 0.5] randomly and independently17,26. To evaluate the stationary state, we simulated the model for 3 × 104 generations, calculated the mean value over the last 1 × 104 generations and averaged the results of 50 independent initial realizations. We confirm that runs for longer time periods did not affect the the presented results.
References
Güth, W., Schmittberger, R. & Schwarze, B. An experimental analysis of ultimatum bargaining. J. Econ. Behav. Organ. 3, 367–388 (1982).
Selten, R. Reexamination of the perfectness concept for equilibrium points in extensive games. Int. J. Gam. Theor. 4, 25–55 (1975).
Page, K. M. & Nowak, M. A. A generalized adaptive dynamics framework can descibe the evolutionary ultimatum game. J. Theor. Biol. 209, 173–179 (2000).
Thaler, R. H. Anomalies: The ultimatum game. J. Econ. Perspect. 2, 195–206 (1988).
Güth, W. & Tietz, R. Ultimatum bargaining behavior: A survey and comparison of experimental results. J. Econ. Psychol. 11, 417–449 (1990).
Roth, A., Prasnikar, V., Okuno-Fujiwara, M. & Zamir, S. Bargaining and market behavior in Jerusalem, Ljubljana, Pittsburg and Tokyo: An experimental study. Am. Econ. Rev. 81, 1068–1095 (1991).
Bolton, G. E. & Zwick, R. Anonymity versus punishment in ultimatum bargaining. Games Econ. Behav. 10, 95–121 (1995).
Fehr, E. & Schmidt, K. A theory of fairness, competition and cooperation. Q. J. Econ. 114, 817–868 (1999).
Camerer, C. F. Behavioral Game Theory: Experiments in Strategic Interaction (Princeton Univ. Press, Princeton, 2003).
Bolton, G. E. A comparative model of bargaining: Theory and evidence. Am. Econ. Rev. 81, 1096–1136 (1991).
Kirchsteiger, G. The role of envy in ultimatum games. J. Econ. Behav. Organ. 25, 373–389 (1994).
Bethwaite, J. & Tompkinson, P. The ultimatum game and non-selfish utility functions. J. Econ. Psychol. 17, 259–271 (1996).
Bolton, G. E. & Ockenfels, A. ERC: A theory of equity, reciprocity and competition. Am. Econ. Rev. 90, 166–193 (2000).
Rubinstein, A. Perfect equilibrium in a bargaining model. Econometrica 50, 97–109 (1982).
Maynard Smith, J. Evolution and the Theory of Games (Cambridge Univ. Press, Cambridge, UK, 1982).
Huck, S. & Oechssler, J. The indirect evolutionary approach to explaining fair allocations. Games Econ. Behav. 28, 13–24 (1999).
Nowak, M. A., Page, K. M. & Sigmund, K. Fairness versus reason in the ultimatum game. Science 289, 1773–1775 (2000).
Page, K. M. & Nowak, M. A. Empathy leads to fairness. Bull. Math. Biol. 64, 1101–1116 (2002).
Page, K. M., Nowak, M. A. & Sigmund, K. The spatial ultimatum game. Proc. R. Soc. Lond. B 267, 2177–2182 (2000).
Killingback, T. & Studer, E. Spatial ultimatum games, collaborations and the evolution of fairness. Proc. R. Soc. Lond. B 268, 1797–1801 (2001).
Sánchez, A. & Cuesta, J. A. Altruism may arise from individual selection. J. Theor. Biol. 235, 233–240 (2005).
Kuperman, M. N. & Risau-Gusman, S. The effect of topology on the spatial ultimatum game. Eur. Phys. J. B 62, 233–238 (2008).
Li, X. & Cao, L. Largest Laplacian eigenvalue predicts the emergence of costly punishment in the evolutionary ultimatum game on networks. Phys. Rev. E 80, 066101 (2009).
Sinatra, R. et al. The ultimatum game in complex networks. J. Stat. Mech. 09, P09012 (2009).
Duan, W.-Q. & Stanley, H. E. Fairness emergence from zero intelligence agents. Phys. Rev. E 81, 026104 (2010).
Gao, J., Li, Z., Wu, T. & Wang, L. The coevolutionary ultimatum game. EPL 93, 48003 (2011).
Iranzo, J., Román, J. & Sánchez, A. The spatial ultimatum game revisited. J. Theor. Biol. 278, 1–10 (2011).
Szolnoki, A., Perc, M. & Szabó, G. Defense mechanisms of empathetic players in the spatial ultimatum game. Phys. Rev. Lett 109, 078701 (2012).
Szolnoki, A., Perc, M. & Szabó, G. Accuracy in strategy imitations promotes the evolution of fairness in the spatial ultimatum game. EPL 100, 28005 (2012).
da Silva, R. & Kellerman, G. A. Analyzing the payoff of a heterogeneous population in the ultimatum game. Braz. J. Phys. 37, 1206–1211 (2007).
Wu, T., Fu, F., Zhang, Y. & Wang, L. Adaptive role switching promotes fairness in networked ultimatum game. Sci. Rep. 3, (2013).
Smith, E. A. et al. Wealth transmission and inequality among hunter-gatherers. Curr. Anthropol. 51, 19–34 (2010).
Nowak, M. A. & May, R. M. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992).
Ohtsuki, H., Hauert, C., Lieberman, E. & Nowak, M. A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006).
Nowak, M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006).
Szabó, G. & Fáth, G. Evolutionary games on graphs. Phys. Rep. 446, 97–216 (2007).
Santos, F. C., Santos, M. D. & Pacheco, J. M. Social diversity promotes the emergence of cooperation in public goods games. Nature 454, 213–216 (2008).
Nowak, M. A., Tarnita, C. E. & Antal, T. Evolutionary dynamics in structured populations. Phil. Trans. R. Soc. B 365, 19–30 (2010).
Perc, M., Gómez-Gardeñes, J., Szolnoki, A., Floría, L. M. & Moreno, Y. Evolutionary dynamics of group interactions on structured populations: a review. J. R. Soc. Interface 10, 20120997 (2013).
Dornic, I., Chaté, H., Chave, J. & Hinrichsen, H. Critical coarsening without surface tension: The universality class of the voter model. Phys. Rev. Lett. 87, 045701 (2001).
Killingback, T., Doebeli, M. & Knowlton, N. Variable investment, the continuous prisoner's dilemma and the origin of cooperation. Proc. R. Soc. Lond. B 266, 1723–1728 (1999).
Gammaitoni, L., Hänggi, P., Jung, P. & Marchasoni, F. Stochastic resonance. Rev. Mod. Phys. 70, 223–287 (1998).
Traulsen, A., Röhl, T. & Schuster, H. G. Stochastic gain in population dynamics. Phys. Rev. Lett. 93, 028701 (2004).
Perc, M. Spatial coherence resonance in excitable media. Phys. Rev. E 72, 016207 (2005).
Szabó, G., Vukov, J. & Szolnoki, A. Phase diagrams for an evolutionary prisoner's dilemma game on two-dimensional lattices. Phys. Rev. E 72, 047107 (2005).
Perc, M. Coherence resonance in spatial prisoner's dilemma game. New J. Phys. 8, 22 (2006).
Santos, F. C. & Pacheco, J. M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 95, 098104 (2005).
Rand, D. G., Tarnita, C. E., Ohtsuki, H. & Nowak, M. A. Evolution of fairness in the one-shot anonymous ultimatum game. Proc. Natl. Acad. Sci. USA 110, 2581–2586 (2013).
Binmore, K., Shaked, A. & Sutton, J. Testing noncooperative bargaining theory: A preliminary study. Am. Econ. Rev. 75, 1178–1180 (1985).
Neelin, J., Sonnenschein, H. & Spiegel, M. A further test of noncooperative bargaining theory: Comment. Am. Econ. Rev. 78, 824–836 (1988).
Ochs, J. & Roth, A. E. An experimental study of sequential bargaining. Am. Econ. Rev. 79, 355–384 (1989).
Mitzkewitz, M. & Nagel, R. Experimental results on ultimatum games with incomplete information. Int. J. Gam. Theor. 22, 171–198 (1993).
Croson, R. T. Information in ultimatum games: An experimental study. J. Econ. Behav. Organ. 30, 197–212 (1996).
Acknowledgements
The authors are supported by National 973 Program (2012CB821203) and NSFC (61020106005, 61375120, 61203374 and 11161011).
Author information
Authors and Affiliations
Contributions
X.W., X.C. and L.W. conceived and designed the study and carried out the research. All authors contributed to writing the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported license. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Wang, X., Chen, X. & Wang, L. Random allocation of pies promotes the evolution of fairness in the Ultimatum Game. Sci Rep 4, 4534 (2014). https://doi.org/10.1038/srep04534
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04534
This article is cited by
-
Individual mobility promotes punishment in evolutionary public goods games
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

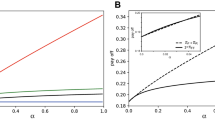

 and the average acceptance threshold
and the average acceptance threshold  of the population as a function of the parameter Λ, if local random allocation scheme is adopted. Error bars indicate the standard deviation. Other parameters: K = 0.1 and ε = 0.005.
of the population as a function of the parameter Λ, if local random allocation scheme is adopted. Error bars indicate the standard deviation. Other parameters: K = 0.1 and ε = 0.005.

 and the average acceptance threshold
and the average acceptance threshold  of the population as a function of the parameter Λ, if global random allocation scheme is adopted. Error bars indicate the standard deviation. Other parameters: K = 0.1 and ε = 0.005.
of the population as a function of the parameter Λ, if global random allocation scheme is adopted. Error bars indicate the standard deviation. Other parameters: K = 0.1 and ε = 0.005.