Introduction

Cellular automata – discrete models that follow a set of rules1 – have been analyzed in various dynamical systems in physics, as well as in computational models and theoretical biology; well-known examples include crystal growth and the Belousov-Zhabotinsky reaction. To simulate quantum mechanical phenomena, Feynman2 proposed a quantum cellular automaton (the Feynman checkerboard). This model, defined in the general case by Meyer3, is known as the discrete-time quantum walk (DTQW). Since the DTQW on a graph is a model of a universal quantum computation4,5, it is of great utility, especially in quantum information6,7,8,9. Furthermore, the DTQW has been demonstrated experimentally in various physical systems10,11,12,13,14,15,16,17,18,19,20,21,22,23,24 to reveal quantum nature under dynamical systems.

As the cellular automaton can be mapped to various differential equations by taking the continuous limit, some DTQW models can be mapped to the Dirac equation25,26,27, the spatially discretized Schrödinger equation28,29, the Klein-Gordon equation27,30, or various other differential equations31,32. These equations have ballistic transport properties, which are reflected mathematically in the one-dimensional (1D) DTQW with a time- and spatial-independent coin operator, i.e. a 1D homogeneous DTQW33. We consider here the 1D DTQW model. Physically, the standard deviation of the homogeneous DTQW is σ(t) ~ t, whereas the unbiased classical random walk has a standard deviation of .

In the homogeneous DTQW, the time evolution of a quantum particle (walker) is given by a unitary operator U defined on the composite Hilbert space , where is the walker Hilbert space and is the two-dimensional coin Hilbert space. For a unitary operator U, the quantum state evolves in each time step t by

with

where the upper (lower ) component corresponds to the left (right) coin state at the j-th site at time step t. As an example, the time evolution of the DTQW is given by

The j-th site probability at time step t is given by and is satisfied for each time step t.

As a generalization of Eq. (3), we define a DTQW with a feed-forward quantum coin described by

with the site-dependent rate function

which incorporates the nearest-neighbor interactions. Since this quantum coin depends on the probability distribution of the coin states on the nearest-neighbor sites at the previous step, this model is called a feed-forward DTQW. It is remarked that the feed-forward DTQW is one of the nonlinear DTQW models. Note that if we set the rate function to g = cos θ, which is time and site independent, then the model in Eq. (4) reduces to the homogeneous model in Eq. (3). We will show that our proposed feed-forward DTQW is experimentally feasible. Furthermore, we will show that this model shows the anomalous diffusion as introduced below.

One of the famous anomalous diffusion equations is the porous medium equation (PME)34, defined by

where the real parameter m > 1 characterizes the degree of porosity of the porous medium. It is known that the PME can be derived from three physical equations for the density ρ, pressure p and velocity v of the gas flow: the equation of continuity, ∂ρ/∂t + ∇ · (ρv) = 0; Darcy's law, v ∝ −∇p; and the equation of state for a polytropic gas, p ∝ ρν, where ν is the polytropic exponent and m = ν + 1. One of the peculiar features of the PME is the so-called finite propagation, which implies the appearance of a free boundary separating the positive region (p > 0) from the empty region (p = 0).

A well-known solution of the PME is the Barenblatt-Pattle (BP) one35; it is self-similar and its total mass is conserved during evolution. The evolutionary behavior of the BP solution was recently studied in the context of generalized entropies and information geometry36. The BP solution can also be expressed by Tsallis' one-real-parameter (q) generalization of a Gaussian function, i.e., the q-Gaussian37. In the case of 1D space, the BP solution is

with q = 2 − m. Here, is a positive parameter that characterizes the width of the q-Gaussian at time t and is similar to the variance in a standard Gaussian. In other words, the parameter σq(t) characterizes the spread of the q-Gaussian distribution38,39;

which reduces to in the limit of q → 1. Note that in the same limit, the q-Gaussian reduces to the standard Gaussian, and the PME reduces to the standard heat equation ∂p/∂t = ∂2p/∂x2.

In this paper, we analyze a specific feed-forward DTQW with an experimental proposal using the polarized state and optical mode. We show numerically that the probability distributions of the feed-forward DTQW model have anomalous diffusion characterized by σq= 0.5(t) ~ t0.4. These dynamics are consistent with the time evolution of the self-similar solution35 of the PME, which is known to describe well the anomalous diffusion of an isotropic gas through a porous medium. Furthermore, we show analytically that the interference terms in our model help the speedup of the associated Markovian model but does not help the quadratic speedup like the homogeneous DTQW does40. Note that although anomalous diffusion was found numerically in a nonlinear model41, an aperiodic time-dependent coin model42 and the history-dependent coin43 from the time dependence of the variance σq= 1(t), the partial differential equation (PDE) corresponding to their models have not derived due to the lack of the numerical step (about 100 step). Therefore, we have not yet revealed the origin of the anomalous diffusion in the DTQW.

Results

Experimental proposal of feed-forward DTQW

We propose an optical implementation of the feed-forward DTQW. In the simple optical implementation of the homogeneous DTQW, the walker space uses the spatial mode and the coin space does the polarized state. The shift uses the polarized beam splitter and the quantum coin uses the quarter-wave, half-wave and quarter-wave plates, which can arbitrarily rotate the polarized state in the Poincaré sphere. This was experimentally done in Refs. 10,11,12,16,17,18,19,20,21,22.

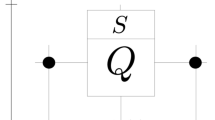
Let us construct the feed-forward system of the quantum coin. The detectors put at each path to evaluate the probability distribution of the coin state and . Since our proposed quantum coin depends on and , we can calculate the coin operator at the jth site. According to the Jones calculation44 to satisfy Eq. (4), we control the angels of the quarter-wave, half-wave and quarter-wave plates for each path. This can be taken as the quantum coin operator with the feed-forward. This is depicted in Fig. 1. In what follows, we consider the long time time evolution of the feed-forward DTQW.

Figure 1
figure 1

Optical implementation of the feed-forward DTQW model.

Figure shows our experimental proposal of our model. From the intensity of the detectors for each path, the polarizers should be changed. This can be taken as the feed-forward quantum coin.

Full size image

Numerical results of feed-forward DTQW with anomalous diffusion

To study the time evolution of the feed-forward DTQW model, the initial state should have nonzero coin states at the nearest-neighbor sites. This can be easily understood by considering the following example. Let us take (, ) as the only non-zero initial state. In this case, the rate is , because there is no neighboring state. From the map in Eq. (4), we see that the nonzero states at t = 1 are and . This gives and we see that the only nonzero state is at t = 2. This state at t = 2 only differs in sign (or phase) from the initial state. Thus if the initial state is concentrated at a single site, no spreading occurs; the state only oscillates around the initial site.

Figure 2 (A) shows a typical probability distribution of the feed-forward DTQW after a long-time evolution. See the Supplementary Movie for more details. The initial state was set as . We note that the probability distribution diffuses very slowly and does not approach a Gaussian. These features are often observed in anomalous diffusion. It is also remarked that such behavior has not yet seen in DTQWs with the position-dependent coin45,46,47,48, which show the localization property.

Figure 2
figure 2

Anomalous slow diffusion of the feed-forward DTQW model.

Its probability distribution at t = 107 step displayed in Panel (A) with running averaged over 10 data sets (light blue line) is fitted by the q-Gaussian (7) with q = 0.5 (red line) to obtain the q-generalized standard deviation σq(t) in Panel (B). Panel (C) shows the long-time evolution of the q-generalized standard deviation σq(t) (green dots), which is well fitted by σq= 0.5(t) ~ t0.4 (red line).

Full size image

We performed long-time numerical simulations of the feed-forward DTQW model [Eq. (4)] for up to t ~ 108 steps. To study the asymptotic behavior, we take running averages of the numerical solutions to reduce the influence of multiple spikes. The averaged data were fitted with the q-Gaussian of Eq. (7) to determine the corresponding q-generalized standard deviation σq(t), as shown in Fig. 2 (B). We note that the averaged data at each time step are well fitted by the q-Gaussian with q = 0.5.

The long-time evolution of σq(t), plotted in Fig. 2 (C), reveals that the time evolution of the feed-forward DTQW model is well characterized by σq= 0.5(t) ~ t0.4, which is the same time dependency for q = 0.5 of the PME [Eq. (8)].

Analytical derivation of anomalous diffusion in the associated Markov model of feed-forward DTQW

The relationship between our model and the PME can be explored using the decomposition method of Romanelli et al.40,49, in which the unitary evolution of a DTQW model is decomposed into Markovian and interference terms. We obtain the following map for both coin distributions and :

where the two terms including are interference terms and is the real part of a complex number z.

Neglecting the interference terms and introducing the abbreviations and , we get the associated Markovian model;

The numerical simulation of the associated Markovian model is performed under initial conditions of and the typical probability distribution shown in Fig. 3 (A) is well fitted by the q-Gaussian with q = 0.0. Furthermore, Fig. 3 (B) shows that the time evolution of σq(t) of the associated Markovian model is well fitted to σq= 0.0(t) ~ t0.33, which again is the same time dependency as the PME for q = 0.

Figure 3
figure 3

Anomalous slow diffusion of the associated Markovian model for the nonlinear quantum walk.

Panel (A) shows the probability distribution of the associated Markovian model at t = 107 step (green dots) fitted by the q-Gaussian, yielding q = 0.0 and σq= 0.0(t) = 283 (red line). Panel (B) shows the long-time evolution of the q-generalized standard deviation σq(t) of the associated Markovian model (blue dots). It is well fitted by σq= 0.0(t) ~ t0.33 (red line).

Full size image

It is known that the classical Markovian model, i.e. one without the interference terms of the homogeneous DTQW, satisfies the standard heat equation in the continuous limit. Consequently, the associated asymptotic probability distribution is a standard Gaussian. This implies that the ballistic transport property of the homogeneous DTQW comes from the interference term40. We thus consider the continuous limit50 of the associated Markovian model.

We introduce the density ρ(x, t) and current j(x, t) as

where Δx is the difference of the nearest-neighbor sites. Taking a Taylor expansion of Eq. (10), we get

in the diffusion limit, i.e., the quantity (Δx)2/Δt remains constant (set to unity here for simplicity) as Δt, Δx → 0 with the one-step time difference Δt. In a similar manner, by expanding Eq. (11) and taking the diffusion limit, we obtain

which implies a breakdown in Fick's first law (j ∝ −∂ρ/∂x) and is the hallmark of anomalous diffusion. By substituting Eq. (14) into Eq. (13), we obtain the following nonlinear PDE:

Evaluating the asymptotic solution of this nonlinear PDE, after a long-time evolution, ρ(x, t) becomes much less than unity. As the rough approximation in this long-time limit, we have 1 − ρ ≈ 1 and ρ2 ≈ 0 and Eq. (15) is thus well approximated by

which is nothing but the PME in Eq. (6) with m = 2 (q = 0). We thus conclude that the approximated asymptotic solution of Eq. (15) is a q-Gaussian with q = 0. In addition, we can show that this result is mathematically valid by applying the asymptotic Lie symmetry method51 (see Method). This method can give an equivalence between the asymptotic solution of the PDE and the analytically-solved one of the other PDE without analytically solving this PDE. Therefore, the associated Markovian model exhibits anomalous diffusion described by the PME in Eq. (6) with m = 2. This implies that the interference term of our model leads to the speed-up of the quantum walker σq= 0.5 ~ t0.4 compared to the associated Markovian model σq= 0 ~ t1/3 and makes the zig-zag shape around the q-Gaussian distribution.

In summary, we have proposed a feed-forward DTQW model Eq. (4) in which the coin operator depends on the coin states of the nearest-neighbor sites. We show that this model is experimentally feasible. Our feed-forward DTQW model asymptotically satisfies the PME for m = 1.5 (q = 0.5) and exhibits anomalous slow diffusion σq= 0.5(t) ~ t0.4 from the probability distribution and the time dependency of the standard deviation defined in the q-Gaussian distribution.

Discussion

In this section, we show that our results after the long-time numerical simulations have no initial coin dependence and that the interference term can be taken as the noise source in addition to the PME. First, while the above analysis uses the only fixed initial coin states as , we numerically confirm that there is almost no dependence of the initial coin state except for the trivial cases as follows. We have performed the several numerical simulations for the initial state specified by and with the real-parameter β and γ ranging from 0 to 1. Note that the trivial cases, β = 0.5, γ = 0 and β = 0, γ = 0.5, lead to the localization of the probability distribution for any time and we cannot define the parameter q for the trivial initial states. Figure 4 shows the numerical evaluation of the parameter q of q-Gaussian distribution from the data at the two different time steps t = 106 and t = 107, under the assumption to satisfy the stationary solution of the PME [Eqs. (7) and (8)]. The evaluated q-parameters for the various initial states are except for the trivial cases. Therefore, we can conclude that our nonlinear model shows the anomalous slow diffusion to satisfy the PME with () without the initial state dependence.

Figure 4
figure 4

Initial coin state dependence.

Changing the parameters β and γ, we numerically evaluate the parameter q of q-Gaussian distribution for 225 different initial states expressed by and . Note that the trivial cases, β = 0.5, γ = 0 and β = 0.5, γ = 1, are not plotted. Our fitting result except for the trivial cases is .

Full size image

Finally, let us consider the difference between the probability distribution of our model and the q-Gaussian distribution with q = 0.5, as shown in Fig. 2 (B); the power spectrum of this difference exhibits a white noise as shown in Fig. 5. This power spectrum divided by the physical time scale t0.4 may remain finite in the asymptotic case, which suggests that our nonlinear model may be mapped to the stochastic PME, i.e. the PME plus a white noise term, in the continuous limit. This stochasticity must come from the interference term. The problem of extracting the stochasticity from a deterministic process has been discussed in another context, that of Mori's noise52. Further analysis of this model may reveal the origin of the stochasticity. This is interesting as a purely mathematical problem of a stochastic nonlinear partial differential equation and for showing the relationship between the discrete model and its continuous limit.

Figure 5
figure 5

The difference between the nonlinear model and the fit.

The power spectrum of the difference between the probability distribution of our model and the q-Gaussian with q = 0.5 at 107 step. To remove the effects of the expectation value, we replace x with x − 36.91 in the q-Gaussian with q = 0.5 [Eq. (7)].

Full size image

Methods

In what follows, the solution of Eq. (15) is asymptotically identical to the solution of Eq. (16). This is mathematically equivalent to showing that the probability distribution

is invariant under an asymptotic Lie symmetry51 of the nonlinear partial differential equation (15). In other words,

In Eq. (17), Z(σq= 0) = 4σq= 0/3 is the normalization factor and in what follows, the argument of this function is omitted where possible and ∂tρ is denoted as ρt for simplicity.

We follow the asymptotic Lie symmetry method and notations in Ref. 51. Under an infinitesimal transformation with the generator

that is

the function ρ(x, t) is mapped to a new function , with

By applying this to the probability distribution Eq. (17), we see that the transformation X with ξ = −x leaves Eq. (17) invariant if and only if

Note that τ = η · t remains unrestricted at this stage because ρ(q = 0)(x) does not explicitly depend on time t. Conversely, the function ρ(x) is invariant under for any τ if and only if ρ(x) is of the form given in Eq. (17).

Following the general procedure for a Lie group analysis of differential equations53, the second prolongation of X is described by

The coefficients Ψt, Ψx and Ψxx are defined as follows. Under an infinitesimal transformation of X, the partial derivatives are transformed as , and . We then readily obtain

The coefficients Ψt, Ψx and Ψxx are then obtained by applying the prolongation formula (2.39) from Ref. 52:

We note that Eq. (18) can be written as

with

The asymptotic Lie symmetry condition

with

can be written in the following compact form:

When the condition in Eq. (30) is fulfilled, each Ak(k = 0, 1, 2, 3) function must vanish separately in the asymptotic limit

implying that the variance σq= 0 also becomes infinity in the asymptotic limit from Eq. (17);

The function A3 can be expressed as

which must be nonzero as σq= 0 → ∞, unless we choose

Making this choice, X becomes

and A3 reduces to

Thus, A3 → 0 as σq= 0 → ∞.

In a similar manner, A0, A1 and A2 are given by

and all become zero as σq= 0 → ∞. Therefore, we conclude that the distribution in Eq. (17) is an invariant solution for the transformation X of Eq. (37), which is an asymptotic symmetry for large |x| of the nonlinear partial differential equation Eq. (18).